1.2 Bomen Algemeen 1.2. BOMEN 7
|
|
|
- Henriette Karen Maes
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 1.2. BOMEN Bomen Algemeen Beschouw eerst een niet-gerichte graaf. Een boom is een samenhangende graaf die geen kringen bevat. Een boom wordt meestal genoteerd met de letter T (tree). Een bos is een graaf waarvan de componenten bomen zijn. De volgende stelling geeft zes equivalente karakteriseringen van het begrip boom. Stelling 1.4 Voor een normale graaf T zijn de volgende zes beweringen equivalent: 1. T is een boom. 2. T heeft geen kringen en heeft n 1 takken. 3. T is samenhangend en heeft n 1 takken. 4. T is samenhangend en na het weglaten van een willekeurige tak niet meer. 5. Ieder paar knooppunten van T is door precies één keten verbonden. 6. T heeft geen kringen, maar door het toevoegen van een willekeurige tak ontstaat precies één kring. Indien n = 1 dan worden de beweringen triviaal. We nemen daarom aan dat n : We moeten bewijzen dat Tn 1 takken heeft en doen dat met inductie (n = 2 triviaal). Door een tak weg te laten ontstaan twee deelgrafen (anders was er een kring) die weer een boom zijn, met n 1 en n 2 knooppunten, waarbij n 1 + n 2 = n. Volgens de inductieveronderstelling hebben deze n 1 1 resp. n 2 1 takken. T heeft dus (n 1 1) + (n 2 1) + 1 = n 1 takken. 2 3: Indien T niet samenhangend is, dan heeft Tk 2 componenten, die geen kringen bevatten, dus een boom zijn. Omdat uit bewering 1 bewering 2 volgt, heeft iedere component één tak minder dan het aantal knooppunten, d.w.z. T heeft n k takken. Anderzijds is het aantal takken van T gelijk aan n 1, waaruit volgt dat k = 1, wat de tegenspraak geeft. 3 4: Stel tak e wordt verwijderd en er is nog steeds samenhang. Dan bevat T e een boom, dus heeft T e minstens n 1 takken, wat de tegenspraak geeft. 4 5: Omdat T samenhangend is, is ieder paar knooppunten door minstens één keten verbonden. Als v en w door twee ketens zijn verbonden, dan is er een kring en dus een tak weg te laten zonder de samenhang te verstoren, wat in tegenspraak is met bewering : Als T kring heeft, dan is er een paar knooppunten dat door twee ketens verbonden is: tegenspraak met bewering 5, dus T heeft geen kringen. Als een tak e wordt toegevoegd, dan ontstaat een kring, want de begin- en eindpunten van e waren al verbonden. Er kunnen ook geen twee kringen ontstaan, want deze zouden beide e bevatten en door beide kringen zonder e te doorlopen zou een kring in T ontstaan.
2 8 HOOFDSTUK 1. GRAFENTHEORIE 6 1: Stel T niet samenhangend. Tak toevoegen tussen knooppunten uit twee verschillende componenten geeft geen kring: tegenspraak. N.B. Waar gebruiken we normaliteit in bovenstaand bewijs? De unieke kring die ontstaat door aan de boom een tak toe te voegen heet een met de boom geassocieerde kring. Een deelgraaf van een samenhangende graaf die een boom is en alle knooppunten van de graaf bevat heet een opspannende boom. Vervolgens beschouwen we een gerichte graaf. Dit is een boom als de bijbehorende niet-gerichte graaf een boom is. Als in een boom voor een knooppunt r geldt dat er een pad is van r naar alle andere knooppunten, dan spreken we over een in r gewortelde gerichte boom. In een in r gewortelde gerichte boom heet knooppunt i een voorganger van knooppunt j als er een pad is van i naar j; in dat geval heet j een afstammeling van i. Als de boom de pijl (i, j) bevat, dan heet i de ouder van j en j een kind van i. Een knooppunt zonder uitgaande pijlen heet een blad, en een knooppunt dat geen blad is heet een inwendig knooppunt. Stelling 1.5 Zij de gerichte graaf T =(V,A) een boom. T is in r gewortelde gerichte boom d.e.s.d. als d (r) =0en d (i) =1voor alle i = r. Iedere i = r heeft minstens één inkomende pijl. Omdat er precies n 1 pijlen zijn moet dus gelden: d (r) =0end (i) = 1 voor alle i = r. Neem een i = r. Omdat we vanuit ieder knooppunt j = r i.v.m. d (j) = 1 kunnen teruglopen, eindigt zo n wandeling in r, d.w.z. in de boom is een pad van r naar i. Vraag 1.7 Laat T een boom zijn. a. dat T minstens twee knooppunten van de graad 1 heeft. b. Veronderstel dat het aantal takken van T even is. dat er minstens één knooppunt met even graad is. Vraag 1.8 dat een boom een bipartiete graaf is. Vraag 1.9 Zij T =(V,F) een opspannende boom van de normale, samenhangende graaf G =(V,E). Toon aan dat geldt: a. Iedere co-kring van G heeft een tak gemeen met F. b. Iedere kring van G heeft een tak gemeen met E\F.
3 24 HOOFDSTUK 1. GRAFENTHEORIE ga verder met VISIT(5) : omdat Z[5] = N[5] krijgen we: S = ; S [5] = 0; COMP[5] = 4; k =5. De streng samenhangende componenten zijn: C 1 = {2, 4, 3}; C 2 = {1}; C 3 = {6} en C 4 = {5}. Stelling 1.19 Algoritme 1.6 heeft complexiteit O(p), waarbij p = max(n, m). Uit Stelling 1.11 volgt dat, zonder de bewerkingen aan Z, S en S mee te tellen, de complexiteit O(p) is. De bewerkingen aan Z zijn: O(n) bij de eerste toekenning in stap 3; stap 4 geeft voor het totale algoritme O(m) en stap 5 O(n). Totaal geeft dit O(p) voor het werk aan Z. Voor het werk aan S en S geldt het volgende. Ieder knooppunt wordt éénmaal op S gezet en er ook éénmaal afgehaald; ieder knooppunt krijgt bij initialisatie de S -waarde 0, dan zodra het bereikt wordt de waarde 1 en tenslotte, nadat het van S is afgehaald weer de waarde 0. Verder wordt voor iedere pijl (v, w) in stap 4b getest of S [w] = 1. De totale hoeveelheid werk aan S en S is dus O(n). Vraag 1.15 Beschouw een gerichte samenhangende graaf G. Toon aan dat G streng samenhangend is d.e.s.d. als iedere pijl van G tot een ronde behoort Minimale opspannende boom Beschouw een niet-gerichte normale samenhangende graaf G = (V,E) waarin aan iedere tak (i, j) eenreëel getal l ij,delengte geheten, is toegekend. Het probleem is om in deze graaf een opspannende boom te vinden met minimale lengte. We zullen twee methoden behandelen, de methode van Prim en de methode van Kruskal. Beide methoden zijn van het type gretig algoritme, d.w.z. dat in iedere iteratiestap een keuze wordt gemaakt die, kortzichtig gezien, het beste is, d.w.z. lokaal optimaal. Het zal blijken dat deze keuzes ook leiden tot een globaal optimum. Voorbeeld 1.12 Beschouw een aantal plaatsen waarvan de onderlinge lengtes in onderstaande tabel staan. Hoe moeten deze plaatsen door electriciteitskabels worden verbonden zódat iedere plaats is aangesloten en er zo weinig mogelijk kabel wordt gebruikt?
4 1.2. BOMEN Voorbeeld 1.13 Beschouw een inlichtingendienst die n agenten heeft zitten in vijandelijk gebied. Als agent i een bericht doorstuurt naar agent j, dan valt dit met kans p ij in vijandelijke handen. Via welke verbindingen moet een bericht worden gecommuniceerd zodat het iedere agent bereikt, terwijl de kans dat het in vijandelijke handen komt minimaal is? Om iedere agent te bereiken moeten de verbindingen minimaal een opspannende boom vormen. Extra verbindingen vergroten de kans dat het bericht in vijandelijke handen valt, dus we zoeken naar de beste opspannende boom T. Voor een gegeven boom T is de kans dat het bericht niet in handen van de vijand komt gelijk aan: (i,j) T (1 p ij). Het probleem luidt dus: max T (i,j) T (1 p ij) max T log (i,j) T (1 p ij) max T (i,j) T log(1 p ij) min T (i,j) T l ij, waarbij l ij = log(1 p ij ), zodat l ij 0 voor alle (i, j). Dit is dus het probleem van de minimale opspannende boom met lengtefunctie l ij = log(1 p ij ) 0 voor alle (i, j). We geven allereerst twee (duale) karakteriseringen van het begrip minimale opspannende boom. Stelling 1.20 Een opspannende boom T heeft minimale lengte d.e.s.d. als voor iedere tak e die niet tot T behoort geldt dat l(e) l(f) voor alle takken f in de kring C T (e) die ontstaat door e aan T toe te voegen. Stel l(e) <l(f) voor een f C T (e). Maar dan is de opspannende boom T {f} + {e} (ga zelf na dat dit een opspannende boom is) een boom met kleinere lengte dan l(t ): tegenspraak. Laat T een opspannende boom zijn met minimale lengte. We moeten aantonen dat l(t )=l(t ) en doen dat met inductie naar k, het aantal takken in T \T. Als k = 0, dan is T = T en klopt de bewering. Nu de algemene inductiestap. Neem e T \T, dan valt T {e } in twee deelbomen uiteen, zeg T 1 en T 2. De keten C T (e )\{e } heeft één eindpunt in T 1 en één eindpunt in T 2.
5 26 HOOFDSTUK 1. GRAFENTHEORIE Dus er is een e T \T en e C T (e )metééneindpuntint 1 en één eindpunt in T 2. Dus T {e } + {e} is weer een opspannende boom. Uit de minimaliteit van T volgt l(e) l(e ), terwijl uit het gegeven van de stelling volgt l(e) l(e ), zodat l(e) =l(e ). We kunnen dus een tak van T vervangen door een tak van T zonder de lengte van de boom te veranderen. Met het inductie argument is hiermee het bewijs geleverd. Stelling 1.21 Een opspannende boom T heeft minimale lengte d.e.s.d. als voor iedere tak e die tot T behoort geldt dat l(e) l(f) voor alle takken f in de snede S T (e) die ontstaat door e uit T te verwijderen. Stel l(e) >l(f) voor een f S T (e). Nu is de opspannende boom T {e}+{f} een opspannende boom met kleinere lengte dan l(t ): tegenspraak. We zullen nu laten zien dat aan de voorwaarde van Stelling 1.20 is voldaan, waaruit volgt dat de opspannende boom minimaal is. Zij e een tak die niet tot T behoort en f = e een element van C T (e). Omdat e S T (f), is volgens het gegeven l(f) l(e). We zullen nu een generiek algoritme opstellen voor het bepalen van een opspannende boom met minimale lengte. Algoritme 1.7 Opspannende boom met minimale lengte (generieke versie) 1. Voor i =1, 2,...,n doe: V i = {i} en T i =. 2. Voor k =1, 2,...,n 1 doe: a. Kies een i met V i =. b. Kies de kleinste tak die precies één uiteinde in V i heeft, zeg tak e, en laat het andere uiteinde in V j zitten. c. V i := V i V j ; V j = ; T i := T i T j {e}; T j =. 3. T = T i en STOP. Stelling 1.22 Algoritme 1.7 is correct, d.w.z. de laatste boom T is een opspannende boom met minimale lengte. We zullen met inductie naar k bewijzen dat alle takken van de deelbomen T i, 1 i n tot een opspannende boom met minimale lengte behoren. Bij de start klopt dit en als de inductiestap is bewezen, dan geldt het ook voor de eindsituatie, d.w.z. voor de boom T.
6 1.2. BOMEN 27 Veronderstel dat in stap k de tak e wordt gekozen met één uiteinde in V i en dat e niet tot een minimale opspannende boom T behoort. De kring C T (e) bevat een tak f = e met één uiteinde in V i. Volgens Stelling 1.20 geldt: l(e) l(f). Anderzijds is e zo gekozen dat l(e) l(f), zodat l(e) =l(f). Dus T = T + {e} {f} is weer een minimale opspannende boom die e bevat: tegenspraak. Opmerking Door in Algoritme 1.7 de mogelijke keuze voor V i nader te specificeren ontstaan diverse algoritmen, waarvan ook de complexiteit kan worden bepaald. De methode van Prim Bij de methode van Prim 4 beginnen we met V 1 en gaan we V 1 steeds uitbreiden met het knooppunt dat er het dichtste bij ligt. De andere V i s blijven dus steeds uit {i} bestaan. De afstand van zo n i tot V 1 noemen we d i en het knooppunt van V 1 dat het dichtste bij i ligt noteren we met w i.dezed i s en w i s worden in iedere iteratie herberekend. Het algoritme is nu als volgt. Algoritme 1.8 Opspannende boom met minimale lengte (Prim) 1. Laat W = {1}, T= ; w i =1,d i = l i1,i=2, 3,...,n. 2. Zolang W = V doe: a. Laat k/ W met k zdd. d k = min i/ W d i. b. W := W {k}; T := T {(k, w k )}. c. Voor iedere i/ W doe: als l ik <d i : d i := l ik en w i := k. Voorbeeld 1.14 Beschouw het probleem uit Voorbeeld 1.12 Iteratie 1: W = {1}, T= ; w i =1, 2 i 7; d 2 = 43, d 3 = 27, d 4 = 60, d 5 = 40, d 6 = 70, d 7 = 50. Iteratie 2: k = 3; W = {1, 3}, T= {(3, 1)}; w 2 =3,d 2 = 28, w 4 =3,d 4 = 26, w 5 =3,d 5 = 14, w 6 =3,d 6 = 35. Iteratie 3: k = 5; W = {1, 3, 5}, T= {(3, 1), (5, 3)}; w 4 =5,d 4 = 19, w 6 =5,d 6 = 24, w 7 =5,d 7 = 40. Iteratie 4: k = 4; W = {1, 3, 5, 4}, T= {(3, 1), (5, 3), (4, 5)}; w 2 =4,d 2 = 20, w 6 =4,d 6 = 18. Iteratie 5: 4 R.C. Prim, Shortest connection networks and some generalizations, Bell Systems Technical Journal 36 (1957)
7 28 HOOFDSTUK 1. GRAFENTHEORIE k = 6; W = {1, 3, 5, 4, 6}, T= {(3, 1), (5, 3), (4, 5), (6, 4)}; w 7 =6,d 7 = 22. Iteratie 6: k = 2; W = {1, 3, 5, 4, 6, 2}, T= {(3, 1), (5, 3), (4, 5), (6, 4), (2, 4)}. Iteratie 7: k = 7; W = {1, 3, 5, 4, 6, 2, 7}, T= {(3, 1), (5, 3), (4, 5), (6, 4), (2, 4), (7, 6)}. De minimale opspannende boom bevat dus de verbindingen (3, 1), (5, 3), (4, 5), (6, 4), (2, 4) en (7, 6). De lengte van de boom is 120. Stelling 1.23 De methode van Prim geeft een minimale opspannende boom en heeft complexiteit O(n 2 ). De correctheid volgt uit Stelling Stap 1 van het algoritme heeft complexiteit O(n). Stap 2 heeft voor iedere iteratie complexiteit O(n), immers: onderdeel a: O(n), onderdeel b: O(1) en onderdeel c: O(n). De methode van Kruskal Bij deze methode 5 worden V i en e zó gekozen dat l(e) minimaal is voor alle mogelijke keuzes. Mogelijke keuzes zijn takken die geen kringen genereren en dus niet beide uiteinden in dezelfde V - verz. hebben. Om dit laatste na te gaan, houden we van alle knooppunten bij in welke component deze zitten: c i = c d.e.s.d. als knooppunt i in de c-de component zit. Het bijhouden van deze componenten gebeurt, indien (i, j) aan T toegevoegd gaat worden (dan bevat T (i, j) dus geen kring), als volgt: 1. als i en j beide niet tot T behoren: i en j komen beide in een nieuwe component; 2. als precies één van de punten i en j tot T behoort, zeg i: j in dezelfde component als i; 3. als i en j beide tot T behoren (en dus in verschillende componenten zitten): alle knooppunten uit de component van j komen in dezelfde component als die van i. Verder sorteren we de takken e k naar oplopende lengte: l(e 1 ) l(e 2 ) l(e m ). Dit geeft het volgende algoritme. Algoritme 1.9 Opspannende boom met minimale lengte (Kruskal) 1. a. W = T = ; c i =0, 1 i n; k = c = 1. b. Sorteer de takken zdd. l(e 1 ) l(e 2 ) l(e m ). 2. Zolang W = V doe: a. Neem e k,zege k =(i, j). 5 J.B. Kruskal, On the shortest spanning subtree of a graph and the traveling salesman problem, Proceedings of the American Mathematical Society 7 (1956)
8 1.2. BOMEN 29 b. Als c i = c j =0: k := k + 1 en herhaal stap 2. c. Als c i = c j =0: T := T {(i, j)} : W := W {i} {j}; c i = c j = c; c := c+1; k := k+1 en herhaal stap 2. d. Als c i =0enc j =0: T := T {(i, j)}; W := W {j}; c j := c i ; k := k +1 en herhaal stap 2. e. Als c i =0enc j =0: T := T {(i, j)}; W := W {i}; c i := c j ; k := k +1 en herhaal stap 2. f. Als c i = c j : T := T {(i, j)}; c p := c i voor alle p W met c p = c j ; k := k +1 en herhaal stap 2. Voorbeeld 1.15 Beschouw het probleem uit Voorbeeld 1.12 Initialisatie: W = T = ; c i =0,i=1, 2,...,7; k = c =1. e 1 =(3, 5), e 2 =(4, 6), e 3 =(4, 5), e 4 =(2, 4), e 5 =(6, 7), e 6 =(2, 7), e 7 =(5, 6), e 8 =(3, 4), e 9 =(1, 3), e 10 =(2, 3), e 11 =(2, 6), e 12 =(3, 6), e 13 =(1, 5), e 14 =(2, 5), e 15 =(4, 7), e 16 =(5, 7), e 17 =(1, 2), e 18 =(1, 7), e 19 =(3, 7), e 20 =(1, 4), e 21 =(1, 6). Iteratie 1: e 1 =(3, 5); T = {(3, 5)}; W = {3, 5}; ;c 3 = c 5 = 1; c = 2; k = 2. Iteratie 2: e 2 =(4, 6); T = {(3, 5), (4, 6)}; W = {3, 5, 4, 6}; c 4 = c 6 = 2; c = 3; k = 3. Iteratie 3: e 3 =(4, 5); T = {(3, 5), (4, 6), (4, 5)}; c 3 = c 5 = 2; k = 4. Iteratie 4: e 4 =(2, 4); T = {(3, 5), (4, 6), (4, 5), (2, 4)}; W = {3, 5, 4, 6, 2}; c 2 = 2; k = 5. Iteratie 5: e 5 =(6, 7); T = {(3, 5), (4, 6), (4, 5), (2, 4), (6, 7)}; W = {3, 5, 4, 6, 2, 7}; c 7 = 2; k = 6. Iteratie 6: e 6 =(2, 7); k = 7. Iteratie 7: e 7 =(5, 6); k = 8. Iteratie 8: e 8 =(3, 4); k = 9. Iteratie 9: e 9 =(1, 3); T = {(3, 5), (4, 6), (4, 5), (2, 4), (6, 7), (1, 3)}; W = {3, 5, 4, 6, 2, 7, 1}; c 1 = 2; k = 10. Stelling 1.24 Algoritme 1.9 geeft een minimale opspannende boom en heeft complexiteit O{max(m log n, n 2 )}. De correctheid volgt weer uit Stelling De initialisatie heeft complexiteit O(m log m) (vanwege het sorteren van m elementen). 6 Omdat log m log n 2 =2log n, is dit ook te schrijven als O(m log n). 6 Zie hiervoor bijvoorbeeld: D.E. Knuth: The art of computer programming, Volume 3: Sorting and searching, Second edition, Addison-Wesley (1998).
9 30 HOOFDSTUK 1. GRAFENTHEORIE Stap 2 wordt O(m) keer uitgevoerd en bestaat uit onderdeel 2a en één van de onderdelen 2b t/m 2f. Afgezien van de opdracht in 2f om de c s aan te passen heeft ieder onderdeel complexiteit O(1). In 2f worden twee bestaande deelbomen tot één boom samengevoegd. Dit kan slechts O(n) keer gebeuren. Het aanpassen van de c-waarden heeft ook complexiteit O(n). Hieruit volgt dat de totale complexiteit van het algoritme O{max(m log n, n 2 )} is. Opmerking: Door een geschikte datastructuur te kiezen is er een implementatie van het algoritme van Kruskal met complexiteit O(m log n). 7 Voor spaarse netwerken, d.w.z. m = O(n) geeft dit een betere complexiteit. Vraag 1.16 Stel dat l(e) <l(f) voor alle f E\{e}. dat e in iedere opspannende boom met minimale lengte zit. Vraag 1.17 Beschouw een netwerk met 10 knooppunten, waarvan de lengtes in onderstaande tabel staan (een - betekent dat er geen verbinding is) a. Bepaal een minimale opspannende boom met de methode van Prim. b. Bepaal een minimale opspannende boom met de methode van Kruskal Opgaven Opgave 1.4 Een samenhangende graaf G =(V,E) metn knooppunten heet éénkringig als G precies één kring bevat. 7 Zie hiervoor paragraaf 23.2 in: T.H. Cormen, C.E. Leiserson, R.L. Rovest and C. Stein: Introduction to algorithms, MIT Press, Cambridge (2001).
10 1.2. BOMEN 31 Toon aan dat de volgende uitspraken equivalent zijn: 1. G is éénkringig. 2. G\e is een opspannende boom voor een geschikt gekozen tak e. 3. G is samenhangend en heeft n takken. 4. G is samenhangend en de verz. C = {e E G\e is samenhangend} is een kring. Opgave 1.5 Laten T 1 en T 2 twee opspannende bomen van G zijn. dat als e een tak is van T 1,ereen tak f van T 2 is zdd. T 1 {e} + {f} ook een opspannende boom van G is. Opgave 1.6 Zij n k het aantal knooppunten met graad k in een boom T die minstens twee knooppunten bevat. dat n 1 n Opgave 1.7 a. Gebruik de gewichten 2, 3, 5, 10 en 10 om te laten zien dat de hoogte van een Huffman boom niet uniek is. b. Hoe kan het algoritme worden aangepast om een Huffman boom met minimale hoogte te krijgen? Opgave 1.8 Zij G een niet-gerichte samenhangende graaf en T de opspannende gerichte boom bestaande uit de pijlen van F, verkregen met DFS. Laat G 1 een deelgraaf van G zijn die volledig is. a. Toon aan dat er in T een pad is waar alle knooppunten van G 1 op liggen. b. Ga na of op dit pad ook andere knooppunten kunnen liggen. Opgave 1.9 a. dat een niet-gerichte graaf bipartiet is d.e.s.d. als iedere kring een even aantal takken heeft. b. Stel een O(p) algoritme op, waarbij p = max(n, m), om na te gaan of een niet-gerichte graaf bipartiet. Opgave 1.10 Zij G een niet-gerichte graaf en T het opspannende gerichte bos bestaande uit de pijlen van F, verkregen met DFS. Zij T [v] het aantal knooppunten dat in T vanuit v kan worden bereikt, inclusief v zelf. a. Toon aan dat w in T vanuit v bereikbaar is d.e.s.d. als N[v] N[w] <N[v]+T [v]. b. Pas algoritme 1.3 aan zdd. daarmee ook de getallen T [v], v V, worden berekend.
11 32 HOOFDSTUK 1. GRAFENTHEORIE Opgave 1.11 Beschouw een gerichte graaf G =(V,A). a. Toon aan dat G geen ronde bevat d.e.s.d. als de verz. D uit DFS leeg is. b. Veronderstel dat D =. Toon aan dat (v, w) A d.e.s.d. R[w] <R[v]. c. Stel een O(p) algoritme op, waarbij p = max(n, m), om de knooppunten zó te nummeren dat als (v, w) A, dan is het nummer van v kleiner dan het nummer van w, indien zo n nummering mogelijk is, d.w.z. als G geen ronde heeft; als dit niet mogelijk is, d.w.z. G heeft wel een ronde, implementeer deze eigenschap dan in het algoritme door een variabele ronde de waarde 1 te geven. Opgave 1.12 Stel een algoritme op voor Breadth-First Search in een niet-gerichte graaf. Opgave 1.13 Pas algoritme 1.6 toe op de gerichte graaf, gerepresenteerd door de volgende lijsten: L[1] = {2}; L[2] = {4, 8}; L[3] = {9}; L[4] = {6, 7}; L[5] = {3, 4}; L[6] = {4}; L[7] = {6}; L[8] = {1, 5}; L[9] = {10}; L[10] = {3, 11}; L[11] = {9}. Opgave 1.14 In deze opgave bespreken we een ander algoritme om de streng samenhangende componenten van een gerichte graaf G =(V,A) te bepalen. Dit algoritme gaat als volgt. Algoritme 1.10 Bepaling streng samenhangende componenten (versie 2) 1. Voer DFS uit en nummer de knooppunten in de volgorde waarin ze worden afgehandeld (het eerst afgehandelde knooppunt krijgt nummer 1 etc). 2. Construeer een andere gerichte graaf G 1 =(V,A 1 )met(v, w) A 1 d.e.s.d. als (w, v) A. 3. Voer DFS uit in G 1, beginnend met het hoogst genummerde knooppunt (volgens de in stap 1 aangebrachte nummering). Indien met een nieuwe boom moet worden gestart, dan beginnen we weer met het nog niet bezochte knooppunt met het hoogste nummer. 4. Neem als s.s.c. de samenhangende componenten die in stap 3 worden gevonden. Beantwoord de volgende vragen over dit algoritme: a. Pas het algoritme toe op Voorbeeld 1.8. b. Bepaal de complexiteit van de methode. c. Toon de correctheid van het algoritme aan.
12 1.2. BOMEN 33 Opgave 1.15 Een bank heeft 5 bijkantoren die elk over een computer terminal beschikken, die verbonden moet worden met de centrale computer in het hoofdkantoor. Deze telecommunicatie geschiedt met speciale telefoonlijnen. Een bijkantoor hoeft niet rechtstreeks met het hoofdkantoor verbonden te zijn, de verbinding kan ook via andere bijkantoren lopen. De kosten van de telefoonlijnen zijn recht evenredig met de lengte van de lijnen. De afstanden tussen de verschillende kantoren staan in onderstaande tabel. hoofdkantoor bijkantoor 1 bijkantoor 2 bijkantoor 3 bijkantoor 4 bijkantoor 5 hoofdkantoor bijkantoor bijkantoor bijkantoor bijkantoor bijkantoor Het probleem is welke verbindingen er gemaakt moeten worden om de kosten te minimaliseren. Los dit probleem op. Opgave 1.16 Een vertrouwelijke boodschap moet door 7 mensen gelezen worden. De boodschap wordt met kans p ij onderschept, als deze regelrecht van persoon i naar j of omgekeerd wordt verstuurd. Hoe sturen we die boodschap rond met een minimale kans dat hij onderschept wordt? De kansen staan in onderstaande tabel gegeven: ,05 0,07 0,03 0,08 0,02 0,05 2-0,09 0,04 0,05 0,05 0,04 3-0,07 0,04 0,08 0,06 4-0,06 0,05 0,05 5-0,07 0,03 6-0, Opgave 1.17 Neem een tweetal knooppunten, zeg s en t, van een graaf G =(V,E) metn knooppunten en een lengtefunctie op de takken. Voor een keten K van s naar t is de waarde van K het maximum van de lengtes op deze keten. Het minmax-probleem is: bepaal een keten van s naar t met minimale waarde. Stel een O(n 2 ) algoritme op om dit probleem op te lossen en bewijs de correctheid van dit algoritme.
13 34 HOOFDSTUK 1. GRAFENTHEORIE Opgave 1.18 De boomgraaf T (G) van een samenhangende graaf G heeft als knooppunten de opspannende bomen van G. Twee knooppunten van T (G) worden verbonden als de bijbehorende opspannende bomen n 2 takken gemeen hebben. a. Toon aan dat voor iedere lengtefunctie l de deelgraaf van T (G) die behoort bij de minimale opspannende bomen samenhangend is. b. Toon aan dat T (G) samenhangend is. Opgave 1.19 Het onderstaande algoritme 8 begint met een bos T met alleen n losse knooppunten, d.w.z. er zijn n componenten. In ieder knooppunt wordt de tak met de kortste lengte gekozen. Deze takken worden aan T toegevoegd. Dit herhaalt zich waarbij in plaats van knooppunten componenten moeten worden genomen en voor iedere component de kortste tak wordt gekozen met precies één uiteinde in die component. Algoritme 1.11 Opspannende boom met minimale lengte (Boruvka) 1. T =(V, ); p = n. 2. Zolang p>1: (i) Voor iedere deelboom T k (1 k p) van T : bepaal de kortste tak met precies één uiteinde in T k,zege k, 1 k p. (ii) Voor k =1, 2,...,p: als e k / T : T := T e k en p := p 1. a. Voer bovenstaand algoritme uit op de graaf uit Voorbeeld b. Toon aan dat als alle lengtes verschillend zijn in T geen kringen voorkomen en het algoritme correct is. c. Geef een voorbeeld waaruit blijkt dat als de lengtes niet verschillend zijn er een kring kan voorkomen en het algoritme dus niet correct is. d. Toon aan dat er hoogstens log 2 n iteraties (het uitvoeren van stap 2) zijn. e. Toon aan dat iedere iteratie met complexiteit O(m) kan worden uitgevoerd, zodat de totale complexiteit O(m log 2 n)is. Opgave 1.20 Beschouw het volgende gerandomiseerde algoritme dat de takken van de graaf met rood en blauw gaat kleuren. Aan het einde van het algoritme vormen de blauwe takken een opspannende boom met minimale lengte. Algoritme 1.12 Opspannende boom met minimale lengte (Kleuralgoritme) Herhaal totdat n 1 takken blauw gekleurd zijn: 8 Dit algoritme stamt al uit 1926 en is ontwikkeld door O. Boruvka (het artikel is in het Tjechisch geschreven).
14 1.3. EULER EN HAMILTON GRAFEN Kies random of wordt verder gegaan met stap 2 of stap Neem een snede S zonder blauwe takken, kies een tak uit S met minimaal gewicht, kleur deze blauw en ga naar stap Neem een kring C zonder rode takken, kies een tak uit C met maximaal gewicht, kleur deze rood en ga naar stap 1. a. Voer bovenstaand algoritme uit op de graaf uit Voorbeeld 1.12 en kies daarbij om en om stap 2 en stap 3. b. dat het algoritme een opspannende boom met minimale lengte oplevert. c. Laat zien dat een variant van bovenstaand algoritme het algoritme van Prim is als we iedere keer stap 2 kiezen met als snede S de takken die grenzen aan een blauw gekleurde tak (start met voor S de takken die knooppunt 1 met de rest van de graaf verbinden). d. Laat zien dat een variant van bovenstaand algoritme het algoritme van Kruskal is als we het volgende doen, nadat de takken in niet-dalende volgorde zijn genummerd: neem de volgende tak; als beide uiteinden blauw in dezelfde blauwe deelboom zitten: voer stap 3 uit met voor C de kring die door het toevoegen van de laatste tak ontstaat; anders voeren we stap 2 uit met voor S de takken tussen de twee deelbomen die door de tak worden verbonden. e. Laat zien dat een variant van bovenstaand algoritme het algoritme van Boruvka is als we het volgende doen: voer stap 2 uit op de snedes die iedere blauwe boom met de rest van de graaf verbinden (start met als blauwe deelbomen alle afzonderlijke knooppunten). 1.3 Euler en Hamilton grafen Euler grafen Niet-gerichte Euler grafen Königsberger bruggenprobleem Door de voormalige Pruisische stad Königsberg stroomt de rivier de Pregel. De oevers van deze rivier en twee eilandjes in de rivier zijn verbonden door zeven bruggen (zie onderstaande figuur). Toen de beroemde Zwitserse wiskundige Euler in 1736 daar op bezoek was werd hem de vraag gesteld of het mogelijk was een wandeling te maken waarbij iedere brug precies één keer wordt aangedaan en bij het beginpunt terugkeert. Door elke rivieroever en elk eiland te representeren door een knooppunt en elke brug door een tak kunnen we er een probleem in een niet-gerichte graaf van maken. De vraag is dan of de graaf een Euler graaf is. Euler 9 wist op deze wijze het probleem op te lossen. 9 L. Euler: Solutio problematis ad geometriam situs pertinentis, Comment. Acad. Sci. Petropol. 8 (1736) Zie ook history/mathematicians/euler.html
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
Grafen. Indien de uitgraad van ieder punt 1 is, dan bevat de graaf een cykel. Indien de ingraad van ieder punt 1 is, dan bevat de graaf een cykel.
 Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Discrete Wiskunde, College 13. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 13 Han Hoogeveen, Utrecht University Algoritme van Kruskal (1) Sorteer de kanten in E op volgorde van lengte; hernummer de kanten zodanig dat c(e 1 ) c(e 2 )... c(e m ) Bij twee
Discrete Wiskunde, College 13 Han Hoogeveen, Utrecht University Algoritme van Kruskal (1) Sorteer de kanten in E op volgorde van lengte; hernummer de kanten zodanig dat c(e 1 ) c(e 2 )... c(e m ) Bij twee
Discrete Wiskunde, College 12. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
A.1 Grafentheorie 64 BIJLAGE A. OPLOSSING VAN DE VRAGEN A.1. GRAFENTHEORIE 65. dan heeft deze kring in ieder knooppunt een even aantal takken).
 64 BIJLAGE A. OPLOSSING VAN DE VRAGEN A. Grafentheorie Vraag. Neem drie knooppunten i, j en k. d(i, k) = het minimum aantal takken in een keten tussen i en k Vraag.2 het minimum aantal takken in een keten
64 BIJLAGE A. OPLOSSING VAN DE VRAGEN A. Grafentheorie Vraag. Neem drie knooppunten i, j en k. d(i, k) = het minimum aantal takken in een keten tussen i en k Vraag.2 het minimum aantal takken in een keten
BESLISKUNDE B. Voorjaar L.C.M. KALLENBERG en F.M. SPIEKSMA
 BESLISKUNDE B Voorjaar 2015 L.C.M. KALLENBERG en F.M. SPIEKSMA UNIVERSITEIT LEIDEN Inhoudsopgave 1 GRAFENTHEORIE 1 1.1 Inleiding.......................................... 1 1.1.1 Niet-gerichte grafen...............................
BESLISKUNDE B Voorjaar 2015 L.C.M. KALLENBERG en F.M. SPIEKSMA UNIVERSITEIT LEIDEN Inhoudsopgave 1 GRAFENTHEORIE 1 1.1 Inleiding.......................................... 1 1.1.1 Niet-gerichte grafen...............................
Tentamen Discrete Wiskunde 1 10 april 2012, 14:00 17:00 uur
 Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Week 1 20-02-2013. Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren.
 Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Tiende college algoritmiek. 14 april Gretige algoritmen
 College 10 Tiende college algoritmiek 1 april 011 Gretige algoritmen 1 Greedy algorithms Greed = hebzucht Voor oplossen van optimalisatieproblemen Oplossing wordt stap voor stap opgebouwd In elke stap
College 10 Tiende college algoritmiek 1 april 011 Gretige algoritmen 1 Greedy algorithms Greed = hebzucht Voor oplossen van optimalisatieproblemen Oplossing wordt stap voor stap opgebouwd In elke stap
l e x e voor alle e E
 Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Tiende college algoritmiek. 26 april Gretige algoritmen
 Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Minimum Opspannende Bomen. Algoritmiek
 Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen 08-04-2005
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
3. Elke lijn van een graaf draagt twee bij tot de som van alle graden.
 Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Bomen. 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen. deel 1. Negende college
 10 Bomen deel 1 Negende college 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen 1 typen bomen Er zijn drie verschillende typen bomen, die in Schaum over verschillende hoofdstukken verdeeld
10 Bomen deel 1 Negende college 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen 1 typen bomen Er zijn drie verschillende typen bomen, die in Schaum over verschillende hoofdstukken verdeeld
V = {a, b, c, d, e} Computernetwerken: de knopen zijn machines in het netwerk, de kanten zijn communicatiekanalen.
 WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
Kortste Paden. Algoritmiek
 Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Tiende college algoritmiek. 2 mei Gretige algoritmen, Dijkstra
 College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Hebzucht loont niet altijd
 Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Uitwerking tentamen Analyse van Algoritmen, 29 januari
 Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
Twaalfde college complexiteit. 11 mei 2012. Overzicht, MST
 College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
Tiende college algoritmiek. 13/21 april Gretige Algoritmen Algoritme van Dijkstra
 Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde II op donderdag 6 juli 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Doorzoeken van grafen. Algoritmiek
 Doorzoeken van grafen Algoritmiek Vandaag Methoden om door grafen te wandelen Depth First Search Breadth First Search Gerichte Acyclische Grafen en topologische sorteringen 2 Doolhof start eind 3 Depth
Doorzoeken van grafen Algoritmiek Vandaag Methoden om door grafen te wandelen Depth First Search Breadth First Search Gerichte Acyclische Grafen en topologische sorteringen 2 Doolhof start eind 3 Depth
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 maart 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 maart 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TUE) en Centrum Wiskunde & Informatica (CWI) 3 en 6 februari 2014 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TUE) en Centrum Wiskunde & Informatica (CWI) 3 en 6 februari 2014 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in
Tentamen combinatorische optimalisatie Tijd:
 Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Lege polygonen in een graaf.
 Uitwerking puzzel 94-2 Lege polygonen in een graaf. Lieke de Rooij Wobien Doyer We hebben n punten die al of niet met elkaar worden verbonden. De bedoeling is om met zo min mogelijk lijnen (=verbindingen)
Uitwerking puzzel 94-2 Lege polygonen in een graaf. Lieke de Rooij Wobien Doyer We hebben n punten die al of niet met elkaar worden verbonden. De bedoeling is om met zo min mogelijk lijnen (=verbindingen)
Radboud Universiteit Nijmegen
 Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde op donderdag 13 april 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Algoritmen aan het werk
 Algoritmen aan het werk (Dag van de wiskunde 24/11/2018) Veerle Fack Universiteit Gent De bevers en de brug Vier bevers willen in het donker een brug oversteken. Ze kunnen de brug slechts alleen of met
Algoritmen aan het werk (Dag van de wiskunde 24/11/2018) Veerle Fack Universiteit Gent De bevers en de brug Vier bevers willen in het donker een brug oversteken. Ze kunnen de brug slechts alleen of met
Tiende college algoritmiek. 4 mei Gretige Algoritmen Algoritme van Dijkstra
 Tiende college algoritmiek mei 018 Gretige Algoritmen Algoritme van Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Tiende college algoritmiek mei 018 Gretige Algoritmen Algoritme van Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Opmerking vooraf: let op, de terminologie is in elk boek weer anders!
 Grafen Opmerking vooraf: let op, de terminologie is in elk boek weer anders! 1. Inleiding Een (ongerichte) graaf (graph) G = (V, E) bestaat uit een eindige, nietlege verzameling V van punten (vertices),
Grafen Opmerking vooraf: let op, de terminologie is in elk boek weer anders! 1. Inleiding Een (ongerichte) graaf (graph) G = (V, E) bestaat uit een eindige, nietlege verzameling V van punten (vertices),
Getaltheorie I. c = c 1 = 1 c (1)
 Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Combinatorische Algoritmen: Binary Decision Diagrams, Deel III
 Combinatorische Algoritmen: Binary Decision Diagrams, Deel III Sjoerd van Egmond LIACS, Leiden University, The Netherlands svegmond@liacs.nl 2 juni 2010 Samenvatting Deze notitie beschrijft een nederlandse
Combinatorische Algoritmen: Binary Decision Diagrams, Deel III Sjoerd van Egmond LIACS, Leiden University, The Netherlands svegmond@liacs.nl 2 juni 2010 Samenvatting Deze notitie beschrijft een nederlandse
Een combinatorische oplossing voor vraag 10 van de LIMO 2010
 Een combinatorische oplossing voor vraag 10 van de LIMO 2010 Stijn Vermeeren (University of Leeds) 16 juni 2010 Samenvatting Probleem 10 van de Landelijke Interuniversitaire Mathematische Olympiade 2010vraagt
Een combinatorische oplossing voor vraag 10 van de LIMO 2010 Stijn Vermeeren (University of Leeds) 16 juni 2010 Samenvatting Probleem 10 van de Landelijke Interuniversitaire Mathematische Olympiade 2010vraagt
Tentamen Discrete Wiskunde
 Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Geldwisselprobleem van Frobenius
 Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Begrenzing van het aantal iteraties in het max-flow algoritme
 Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Discrete Modellen in de Toegepaste Wiskunde (WISB136) Dinsdag 19 april, 2011
 Discrete Modellen in de Toegepaste Wiskunde (WISB136) Dinsdag 19 april, 2011 Geef niet alleen de antwoorden, maar laat ook de afleidingen van de antwoorden zien. Vermeld bij het gebruik van een algoritme
Discrete Modellen in de Toegepaste Wiskunde (WISB136) Dinsdag 19 april, 2011 Geef niet alleen de antwoorden, maar laat ook de afleidingen van de antwoorden zien. Vermeld bij het gebruik van een algoritme
Algoritmiek. 15 februari Grafen en bomen
 Algoritmiek 15 februari 2019 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices) en E een verzameling van
Algoritmiek 15 februari 2019 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices) en E een verzameling van
Minimum Spanning Tree
 Minimum Spanning Tree Wat is MST? Minimum spanning tree De meest efficiënte manier vinden om een verbonden netwerk op te bouwen Wat is een tree/boom? Graaf G: een verzameling knopen (vertices): V een verzameling
Minimum Spanning Tree Wat is MST? Minimum spanning tree De meest efficiënte manier vinden om een verbonden netwerk op te bouwen Wat is een tree/boom? Graaf G: een verzameling knopen (vertices): V een verzameling
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 11 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 11 november 2015 1 / 22 Mededelingen Huiswerk 2 nagekeken Terug
TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 11 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 11 november 2015 1 / 22 Mededelingen Huiswerk 2 nagekeken Terug
l e x e voor alle e E
 Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Greedy algoritmes. Algoritmiek
 Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Uitwerkingen Sum of Us
 Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Examen Discrete Wiskunde donderdag 12 april, 2018
 Examen Discrete Wiskunde 2017-2018 donderdag 12 april, 2018 De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Gebruik hiervoor de ruimte onder de vraag; er is in principe genoeg
Examen Discrete Wiskunde 2017-2018 donderdag 12 april, 2018 De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Gebruik hiervoor de ruimte onder de vraag; er is in principe genoeg
Grafen deel 2 8/9. Zesde college
 Grafen deel 2 8/9 Zesde college 1 Een Eulercircuit is een gesloten wandeling die elke lijn precies één keer bevat. traversable trail all edges distinct 8.5 rondwandeling zeven bruggenprobleem van Köningsbergen
Grafen deel 2 8/9 Zesde college 1 Een Eulercircuit is een gesloten wandeling die elke lijn precies één keer bevat. traversable trail all edges distinct 8.5 rondwandeling zeven bruggenprobleem van Köningsbergen
Workshop DisWis, De Start 13/06/2007 Bladzijde 1 van 7. Sudoku. Sudoku
 DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
Netwerkstroming. Algoritmiek
 Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Bomen. 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen
 10 Bomen 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen 1 Baarn Hilversum Soestdijk Den Dolder voorbeelden route boom beslisboom Amersfoort Soestduinen + 5 * + 5.1 5.2 5.3 5.4 2 3 * * 2 5.3.1
10 Bomen 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen 1 Baarn Hilversum Soestdijk Den Dolder voorbeelden route boom beslisboom Amersfoort Soestduinen + 5 * + 5.1 5.2 5.3 5.4 2 3 * * 2 5.3.1
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2008 2009, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Tweede bachelor Informatica Academiejaar 2008 2009, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Overzicht. 1. Definities. 2. Basisalgoritme. 3. Label setting methoden. 4. Label correcting methoden. 5. Ondergrenzen. 6.
 Overzicht 1. Definities 2. Basisalgoritme 3. Label setting methoden 4. Label correcting methoden 5. Ondergrenzen 6. Resultaten Kortste Pad Probleem 1 Definities Een graaf G = (V, E) bestaat uit een verzameling
Overzicht 1. Definities 2. Basisalgoritme 3. Label setting methoden 4. Label correcting methoden 5. Ondergrenzen 6. Resultaten Kortste Pad Probleem 1 Definities Een graaf G = (V, E) bestaat uit een verzameling
Lijstkleuring van grafen
 C.J. Meerman Lijstkleuring van grafen Bachelorscriptie 10 juni 2010 Email: cjmeerman@gmail.com Scriptiebegeleider: Dr. D. C. Gijswijt Mathematisch Instituut, Universiteit Leiden Inhoudsopgave 1 Inleiding
C.J. Meerman Lijstkleuring van grafen Bachelorscriptie 10 juni 2010 Email: cjmeerman@gmail.com Scriptiebegeleider: Dr. D. C. Gijswijt Mathematisch Instituut, Universiteit Leiden Inhoudsopgave 1 Inleiding
Uitgebreide uitwerking Tentamen Complexiteit, juni 2016
 Uitgebreide uitwerking Tentamen Complexiteit, juni 016 Opgave 1. (3+10++7+6) a. De hoogte van de beslissingsboom (lengte van het langste pad) stelt het aantal arrayvergelijkingen in de worst case voor.
Uitgebreide uitwerking Tentamen Complexiteit, juni 016 Opgave 1. (3+10++7+6) a. De hoogte van de beslissingsboom (lengte van het langste pad) stelt het aantal arrayvergelijkingen in de worst case voor.
Tiende college algoritmiek. 14 april Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS
 Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Elfde college algoritmiek. 10 mei Algoritme van Dijkstra, Gretige Algoritmen
 lgoritmiek 019/lgoritme van ijkstra lfde college algoritmiek 10 mei 019 lgoritme van ijkstra, Gretige lgoritmen 1 lgoritmiek 019/ynamisch programmeren Programmeeropdracht 3 Lange Reis 0 10 10 1 1 100 0
lgoritmiek 019/lgoritme van ijkstra lfde college algoritmiek 10 mei 019 lgoritme van ijkstra, Gretige lgoritmen 1 lgoritmiek 019/ynamisch programmeren Programmeeropdracht 3 Lange Reis 0 10 10 1 1 100 0
Elke gelijkenis met bestaande gebeurtenissen en/of personen berust op louter toeval.
 Leo is een hevige fan van het Belgisch voetbal. Behalve een vurige fan van Blauw Zwart, is hij ook geïnteresseerd in de voetbaltempels van de eersteklassevoetbalclubs. Daarom wil hij, samen met zijn kameraad
Leo is een hevige fan van het Belgisch voetbal. Behalve een vurige fan van Blauw Zwart, is hij ook geïnteresseerd in de voetbaltempels van de eersteklassevoetbalclubs. Daarom wil hij, samen met zijn kameraad
Datastructuren Uitwerking jan
 Datastructuren Uitwerking jan 16 1 1a) Een ADT wordt gekenmerkt door de opgeslagen gegevens en de beschikbare operaties. De Priority Queue bevat en verzameling elementen waarbij elk element en eigen waarde
Datastructuren Uitwerking jan 16 1 1a) Een ADT wordt gekenmerkt door de opgeslagen gegevens en de beschikbare operaties. De Priority Queue bevat en verzameling elementen waarbij elk element en eigen waarde
In dit gedeelte worden drie problemen genoemd die kunnen voorkomen in netwerken.
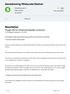 Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
Grafen deel 1. Zesde college
 Grafen deel 1 8 Zesde college 1 buren in Europa 2 http://commons.wikimedia.org/wiki/file:member_states_of_the_european_union_(polar_stereographic_projection)_en.svg buren in Europa FI SE EE PT IE GB DK
Grafen deel 1 8 Zesde college 1 buren in Europa 2 http://commons.wikimedia.org/wiki/file:member_states_of_the_european_union_(polar_stereographic_projection)_en.svg buren in Europa FI SE EE PT IE GB DK
Netwerkstroming. Algoritmiek
 Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Tweede college algoritmiek. 12 februari Grafen en bomen
 College 2 Tweede college algoritmiek 12 februari 2016 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices)
College 2 Tweede college algoritmiek 12 februari 2016 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices)
Hoofdstuk!7!Kortste!paden!
 oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2012 2013, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2012 2013, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Uitgebreide uitwerking Tentamen Complexiteit, juni 2017
 Uitgebreide uitwerking Tentamen Complexiteit, juni 017 Opgave 1. a. Een pad van de wortel naar een blad stelt de serie achtereenvolgende arrayvergelijkingen voor die het algoritme doet op zekere invoer.
Uitgebreide uitwerking Tentamen Complexiteit, juni 017 Opgave 1. a. Een pad van de wortel naar een blad stelt de serie achtereenvolgende arrayvergelijkingen voor die het algoritme doet op zekere invoer.
Divide & Conquer: Verdeel en Heers vervolg. Algoritmiek
 Divide & Conquer: Verdeel en Heers vervolg Algoritmiek Algoritmische technieken Vorige keer: Divide and conquer techniek Aantal toepassingen van de techniek Analyse met Master theorem en substitutie Vandaag:
Divide & Conquer: Verdeel en Heers vervolg Algoritmiek Algoritmische technieken Vorige keer: Divide and conquer techniek Aantal toepassingen van de techniek Analyse met Master theorem en substitutie Vandaag:
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
Kortste Paden. Algoritmiek
 Kortste Paden Vandaag Kortste Paden probleem All pairs / Single Source / Single Target versies DP algoritme voor All Pairs probleem (Floyd s algoritme) Dijkstra s algoritme voor Single Source Negatieve
Kortste Paden Vandaag Kortste Paden probleem All pairs / Single Source / Single Target versies DP algoritme voor All Pairs probleem (Floyd s algoritme) Dijkstra s algoritme voor Single Source Negatieve
Het minimale aantal sleutels op niveau h is derhalve
 1 (a) In een B-boom van orde m bevat de wortel minimaal 1 sleutel en maximaal m 1 sleutels De andere knopen bevatten minimaal m 1 sleutels en maximaal m 1 sleutels (b) In een B-boom van orde 5 bevat elke
1 (a) In een B-boom van orde m bevat de wortel minimaal 1 sleutel en maximaal m 1 sleutels De andere knopen bevatten minimaal m 1 sleutels en maximaal m 1 sleutels (b) In een B-boom van orde 5 bevat elke
Opdracht 1 Topics on Parsing and Formal Languages - fall 2010
 Opdracht 1 Topics on Parsing and Formal Languages - fall 2010 Rick van der Zwet 8 december 2010 Samenvatting Dit schrijven zal uitwerkingen van opgaven behandelen uit het boek [JS2009]
Opdracht 1 Topics on Parsing and Formal Languages - fall 2010 Rick van der Zwet 8 december 2010 Samenvatting Dit schrijven zal uitwerkingen van opgaven behandelen uit het boek [JS2009]
Gödels theorem An Incomplete Guide to Its Use and Abuse, Hoofdstuk 3
 Gödels theorem An Incomplete Guide to Its Use and Abuse, Hoofdstuk 3 Koen Rutten, Aris van Dijk 30 mei 2007 Inhoudsopgave 1 Verzamelingen 2 1.1 Definitie................................ 2 1.2 Eigenschappen............................
Gödels theorem An Incomplete Guide to Its Use and Abuse, Hoofdstuk 3 Koen Rutten, Aris van Dijk 30 mei 2007 Inhoudsopgave 1 Verzamelingen 2 1.1 Definitie................................ 2 1.2 Eigenschappen............................
Algoritmes in ons dagelijks leven. Leve de Wiskunde! 7 April 2017 Jacobien Carstens
 Algoritmes in ons dagelijks leven Leve de Wiskunde! 7 April 2017 Jacobien Carstens Wat is een algoritme? Een algoritme is een eindige reeks instructies die vanuit een gegeven begintoestand naar een beoogd
Algoritmes in ons dagelijks leven Leve de Wiskunde! 7 April 2017 Jacobien Carstens Wat is een algoritme? Een algoritme is een eindige reeks instructies die vanuit een gegeven begintoestand naar een beoogd
Discrete modellen in de toegepaste wiskunde (WISB136) Uitwerkingen proeftentamen.
 Discrete modellen in de toegepaste wiskunde (WISB6) Uitwerkingen proeftentamen. Docent: Rob H. Bisseling april 202. Begin met een matching M = {x y, x y, x 6 y 6 } aangegeven door de vette lijnen. x De
Discrete modellen in de toegepaste wiskunde (WISB6) Uitwerkingen proeftentamen. Docent: Rob H. Bisseling april 202. Begin met een matching M = {x y, x y, x 6 y 6 } aangegeven door de vette lijnen. x De
Optimaliseren in Netwerken
 Optimaliseren in Netwerken Kees Roos e-mail: C.Roos@tudelft.nl URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Optimaliseren in Netwerken Kees Roos e-mail: C.Roos@tudelft.nl URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Uitwerking Puzzel 93-1, Doelloos
 Uitwerking Puzzel 93-1, Doelloos Wobien Doyer Lieke de Rooij Volgens de titel is deze puzzel zonder doel, dus zonder bekende toepassing. Het doel is echter nul en dat is zeker in de wiskunde niet niks.
Uitwerking Puzzel 93-1, Doelloos Wobien Doyer Lieke de Rooij Volgens de titel is deze puzzel zonder doel, dus zonder bekende toepassing. Het doel is echter nul en dat is zeker in de wiskunde niet niks.
Opdracht 1 Topics on Parsing and Formal Languages - fall 2010
 Opdracht 1 Topics on Parsing and Formal Languages - fall 2010 Rick van der Zwet 13 november 2010 Samenvatting Dit schrijven zal uitwerkingen van opgaven behandelen uit het boek [JS2009]
Opdracht 1 Topics on Parsing and Formal Languages - fall 2010 Rick van der Zwet 13 november 2010 Samenvatting Dit schrijven zal uitwerkingen van opgaven behandelen uit het boek [JS2009]
Het Chinese Postbode Probleem. Marene Dimmendaal s
 Het Chinese Postbode Probleem Marene Dimmendaal s4419553 Nijmegen 2018 Het Chinese Postbode Probleem Marene Dimmendaal s4419553 Bachelorscriptie Wiskunde aan de Radboud Universiteit te Nijmegen Geschreven
Het Chinese Postbode Probleem Marene Dimmendaal s4419553 Nijmegen 2018 Het Chinese Postbode Probleem Marene Dimmendaal s4419553 Bachelorscriptie Wiskunde aan de Radboud Universiteit te Nijmegen Geschreven
Optimalisering/Besliskunde 1. College 1 6 september, 2012
 Optimalisering/Besliskunde 1 College 1 6 september, 2012 Algemene informatie College: donderdag 9:00-10:45: Gorlaeus C1/C2, Leiden vrijdag: werkcollege Leiden en Delft vragenuur Delft Vier verplichte huiswerkopgaven
Optimalisering/Besliskunde 1 College 1 6 september, 2012 Algemene informatie College: donderdag 9:00-10:45: Gorlaeus C1/C2, Leiden vrijdag: werkcollege Leiden en Delft vragenuur Delft Vier verplichte huiswerkopgaven
Heuristieken en benaderingsalgoritmen. Algoritmiek
 Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Elfde college complexiteit. 23 april NP-volledigheid III
 college 11 Elfde college complexiteit 23 april 2019 NP-volledigheid III 1 TSP Als voorbeeld bekijken we het Travelling Salesman/person Problem, ofwel het Handelsreizigersprobleem TSP. Hiervoor geldt: TSP
college 11 Elfde college complexiteit 23 april 2019 NP-volledigheid III 1 TSP Als voorbeeld bekijken we het Travelling Salesman/person Problem, ofwel het Handelsreizigersprobleem TSP. Hiervoor geldt: TSP
De statespace van Small World Networks
 De statespace van Small World Networks Emiel Suilen, Daan van den Berg, Frank van Harmelen epsuilen@few.vu.nl, daanvandenberg1976@gmail.com, Frank.van.Harmelen@cs.vu.nl VRIJE UNIVERSITEIT AMSTERDAM 2 juli
De statespace van Small World Networks Emiel Suilen, Daan van den Berg, Frank van Harmelen epsuilen@few.vu.nl, daanvandenberg1976@gmail.com, Frank.van.Harmelen@cs.vu.nl VRIJE UNIVERSITEIT AMSTERDAM 2 juli
Oefeningen Discrete Wiskunde - Hoofdstuk 6 - Peter Vandendriessche Fouten, opmerkingen of alternatieve methodes? me:
 Oefeningen Discrete Wiskunde - Hoofdstuk 6 - Peter Vandendriessche Fouten, opmerkingen of alternatieve methodes? Email me: peter.vdd@telenet.be 1. Het aantal knoop-tak overgangen is altijd even. De totaalsom
Oefeningen Discrete Wiskunde - Hoofdstuk 6 - Peter Vandendriessche Fouten, opmerkingen of alternatieve methodes? Email me: peter.vdd@telenet.be 1. Het aantal knoop-tak overgangen is altijd even. De totaalsom
Oefening 4.3. Zoek een positief natuurlijk getal zodanig dat de helft een kwadraat is, een derde is een derdemacht en een vijfde is een vijfdemacht.
 4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 = 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 = 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
1 Vervangingsstrategie auto
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2002 1 Vervangingsstrategie auto Onderdeel a Zij V = {0, 1, 2, 3, 4, 5, 6}, waarbij knoop i staat voor het einde
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2002 1 Vervangingsstrategie auto Onderdeel a Zij V = {0, 1, 2, 3, 4, 5, 6}, waarbij knoop i staat voor het einde
Bomen. 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen. deel 2. Tiende college
 10 Bomen deel 2 Tiende college 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen 1 arboretum ongericht 8.8 tree graphs 9.4 rooted trees ch.10 binary trees 2 gericht geordend links/rechts bomen
10 Bomen deel 2 Tiende college 8.8 ongerichte bomen 9.4 gerichte bomen ch 10. binaire bomen 1 arboretum ongericht 8.8 tree graphs 9.4 rooted trees ch.10 binary trees 2 gericht geordend links/rechts bomen
Lijst-kleuringen in de grafentheorie
 Lijst-kleuringen in de grafentheorie Berrie Bottelier 16 juli 2014 Bachelorscriptie Begeleiding: dr. Guus Regts 4 5 6 1 2 3 Korteweg-de Vries Instituut voor Wiskunde Faculteit der Natuurwetenschappen,
Lijst-kleuringen in de grafentheorie Berrie Bottelier 16 juli 2014 Bachelorscriptie Begeleiding: dr. Guus Regts 4 5 6 1 2 3 Korteweg-de Vries Instituut voor Wiskunde Faculteit der Natuurwetenschappen,
Onderwerpen. Punten en lijnen, postbodes en handelsreizigers. Theorie. Theorie (2) Graaftheorie. Een mini-inleiding graaftheorie
 Onderwerpen Punten en lijnen, postbodes en handelsreizigers Een mini-inleiding graaftheorie Graaftheorie Herman Geuvers Euler en de postbode Radboud Universiteit Nijmegen 9 februari 2019 met dank aan Engelbert
Onderwerpen Punten en lijnen, postbodes en handelsreizigers Een mini-inleiding graaftheorie Graaftheorie Herman Geuvers Euler en de postbode Radboud Universiteit Nijmegen 9 februari 2019 met dank aan Engelbert
Elfde college algoritmiek. 28 april Gretige Algoritmen, Algoritme van Dijkstra, Branch & Bound
 lgoritmiek 01/retige lgoritmen lfde college algoritmiek 8 april 01 retige lgoritmen, lgoritme van ijkstra, ranch & ound 1 lgoritmiek 01/retige lgoritmen Minimale opspannende boom egeven een samenhangende,
lgoritmiek 01/retige lgoritmen lfde college algoritmiek 8 april 01 retige lgoritmen, lgoritme van ijkstra, ranch & ound 1 lgoritmiek 01/retige lgoritmen Minimale opspannende boom egeven een samenhangende,
ALGORITMIEK: antwoorden werkcollege 5
 ALGORITMIEK: antwoorden werkcollege 5 opgave 1. a. Brute force algoritme, direct afgeleid uit de observatie: loop v.l.n.r. door de tekst; als je een A tegenkomt op plek i (0 i < n 1), loop dan van daaruit
ALGORITMIEK: antwoorden werkcollege 5 opgave 1. a. Brute force algoritme, direct afgeleid uit de observatie: loop v.l.n.r. door de tekst; als je een A tegenkomt op plek i (0 i < n 1), loop dan van daaruit
