Informatica: C# WPO 4
|
|
|
- Gerrit Peeters
- 9 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Informatica: C# WPO 4 1. Inhoud For-loop, debuggen, inleiding tot graphics 2. Oefeningen Demo 1: Geometrische figuren Demo 2: Teken een 10 bij 10 rooster Demo 3: Debug oplossingen demo s 1 en 2 A: Flowerpower A: Vierkant n A: Arceer de canvas! A: Progressbar E: Schaakbord E: Teken gestreepte ruit X: Integraal Een speciale dank gaat naar Jelle De Decker voor een aantal aangeleverde afbeeldingen. 2.1 Demo 1: Geometrische figuren In deze demo wordt het tekenen van eenvoudige geometrische figuren aangetoond. Om te tekenen wordt er een canvas op het formulier geplaatst. Verander de achtergrondskleur naar de gewenste kleur (hier zwart). Teken een horizontale witte lijn, waarop een rechthoek wordt getekend. Hiernaast wordt ook een rode bol getekend. Hint 1: Het assenkruis om te tekenen (canvas) is als volgt: het nulpunt van de tekening bevindt zich linksboven, horizontaal loopt de x-as van links naar rechts, verticaal loopt de y-as van boven naar beneden, dit betekent dat er in de verticale richting omgekeerd getekend wordt (spiegelen). Om een tekening volgens de y-as te plotten, vindt volgende omzetting plaats: y plot = Height canvas y (1) 1
2 2.2 Demo 2: Teken een 10 bij 10 rooster Teken een rooster van 10 bij 10 cellen (figuur 1). Gebruik hiervoor een canvas (=tekenoppervlak) van 600 bij 600 pixels. Elke cel is 0 bij 0 pixels groot. Figuur 1: Voorbeeld programma 2.3 Demo 3: Debug oplossingen demo s 1 en 2 Om de correctheid van de code na te gaan, worden voorgaande oplossingen gedebugged. Debuggen in C# kan men via onderstaande werkwijzen: Breakpoints: een rood bolletje in de kantlijn van de code. Het programma zal hier stoppen tijdens de uitvoering. Eens de breakpoint bereikt is, kan men de code stap voor stap uitvoeren. Tijdens het debuggen (breakpoint, stap voor stap uitvoeren), kan men de waarde van de variabelen opvragen in de watch list. 2.4 A: Flowerpower In deze opgave wordt er gevraagd om een bloem te tekenen (zie figuur 2). Om de bloem te tekenen ga je als volgt te werk: Teken 4 gevulde cirkels van dezelfde kleur. De stuiver teken je in het geel en in het midden van de bloem. 2
3 De steel laat je van helemaal beneden tot het midden van de bloem tekenen (merk dat de steel als eerste getekend moet worden). Voeg 2 blaadjes toe onderaan de steel. De bloembladen zijn elk 100 pixels groot en staan zelf 0 pixels uit elkaar. De stuiver is zelf 7 pixels groot en de steel neem je pixels breed. De gewone bladen mag je 2 pixels groot nemen. Het effect van overlap kan je maken door de kleuren doorzichtig te nemen. Dit kan je doen door (bloembladeren): Codefragment 1: Bloembladen keuren geven 1 blad.fill = new SolidColorBrush(Color.FromArgb(10, 0, 10, 10)); Hierbij teken je de bloem 100 pixels van de linker- en bovenrand. Figuur 2: Output flowerpower 2. A: Vierkant n Schrijf een programma waarin je vierkantjes in vierkantjes kan tekenen. Nadat je een vierkant getekend hebt, teken je het volgende vierkant waarbij de zijden 0.9 zo groot zijn als het net getekende vierkant. Teken zoveel vierkant als opgegeven door de gebruiker in een tekstbox (zie figuur 3). Het eerste vierkant (buitenste) dat getekend wordt heeft zijden die 0.9 de breedte van de canvas heeft. Voor de canvas neem je de hoogte en breedte gelijk (zie properties window). 3
4 Figuur 3: Vierkant n 2.6 A: Arceer de canvas! Arceer het tekenoppervlak (=canvas) door schuine strepen te tekenen. Laat de gebruiker om zelf de interlinie tussen de strepen te bepalen. Figuur 4: Voorbeeld programma 2.7 A: Progressbar Teken op een witte canvas een horizontale balk die van zwart naar rood kleurt. De balk is 100 pixels hoog en neemt de volledige breedte van de canvas in. Om de kleuren te bekomen, kan volgende truck toegepast worden: Verdeel de balk in 2 gelijke delen (rechthoekjes). Elk rechthoekje heeft zijn eigen kleur. 4
5 Hoe rechtser de rechthoek, hoe roder de kleur. Hint: Om zelf kleuren in te stellen, kan men onderstaande code gebruiken. Codefragment 2: Manueel kleuren aanmaken in C# 1 // R = byte from 0 to 2 - red component 2 // G = byte from 0 to 2 - green component 3 // B = byte from 0 to 2 - blue component 4 byte R = (byte)i; // i = index of for loop byte G = 0; 6 byte B = 0; 7 Color kleur = Color.FromArgb(2,R,G,B); Hint: Om verticale strepen tussen de schakkeringen te vermijden kan je best de breedte van de balkjes met 1 pixels breder maken. Figuur : Voorbeeld programma 2.8 E: Schaakbord Teken een schaakbord door gebruik te maken van rode en groene vierkantjes die elkaar afwisselen (figuur 6). Elk vierkantje is 0 bij 0 pixels groot. Figuur 6: Voorbeeld programma
6 2.9 E: Teken gestreepte ruit Teken de ruit zoals afgebeeld in onderstaande afbeelding. De grootte van de ruit wordt ingegeven door de gebruiker alsook het aantal verticale strepen in de ruit. Figuur 7: Voorbeeld programma Uitbreiding: Kunnen horizontale strepen getekend worden? Het aantal horizontale strepen is onafhankelijk van het aantal verticale strepen X: Integraal In deze opgave wordt er gevraagd om de oppervlakte onder de sinusfunctie van x = [0, π] te berekenen. De wiskundige benadering van (zie Basiswiskunde) wordt gegeven in formule 2. A = π 0 sin(x)dx (2) Deze integraal wordt in deze opgave via een for-loop benaderd, zoals (wiskundig) weergegeven in formule 3 i<n A = sin(i i ) i (3) i=0 Concreet betekent dit dat je de integraal/oppervlakte berekent door zeer dunne rechthoeken met elkaar op te tellen. De breedte van elke rechthoek komt overeen met i, terwijl de hoogte overeenkomt met de functie op die plaats. De som wordt hierbij beperkt door het aantal stappen (n) die genomen worden voor deze integraal. Indien men voor de berekening van deze integraal (n is dus gelijk aan ) stappen wil nemen, dan komt de breedte i overeen met π. Hieronder wordt een voorbeeld gegeven van deze integraal, waarbij i = π. 6
7 i x = i i sin(x) Lokale oppervlakte A i Totale oppervlakte A π π π π Tabel 1: Berekenen van de integraal in stappen van i = π Hoe kleiner i genomen wordt, hoe meer stappen nodig zijn om de integraal te berekenen. Daardoor kan de integraal veel nauwkeuriger bepaald worden. Bereken deze integraal en geef het resultaat weer. 1 i
Objectgeoriënteerd Programmeren: WPO 1
 Objectgeoriënteerd Programmeren: WPO 1 1. Inhoud Opfrissing syntax, programmeermethodes, datatypes, functies/procedures, tekenen in C#. Herhaling Informatica 1 ste bachelor. 2. Oefeningen Demo 1: Volume
Objectgeoriënteerd Programmeren: WPO 1 1. Inhoud Opfrissing syntax, programmeermethodes, datatypes, functies/procedures, tekenen in C#. Herhaling Informatica 1 ste bachelor. 2. Oefeningen Demo 1: Volume
Informatica: C# WPO 5
 Informatica: C# WPO 5 1. Inhoud While-loop, do while, debuggen, graphics 2. Oefeningen Demo 1: Power of 2 Demo 2: Tel totdat... Demo 3: Debug oplossing demo s 1 en 2 A: Count down A: Random counting A:
Informatica: C# WPO 5 1. Inhoud While-loop, do while, debuggen, graphics 2. Oefeningen Demo 1: Power of 2 Demo 2: Tel totdat... Demo 3: Debug oplossing demo s 1 en 2 A: Count down A: Random counting A:
Objectgeoriënteerd Programmeren: WPO 1
 Objectgeoriënteerd Programmeren: WPO 1 1. Inhoud Opfrissing syntax, programmeermethodes, datatypes, functies/procedures, tekenen in C#. Herhaling Informatica 1 ste bachelor. 2. Oefeningen Demo 1: Volume
Objectgeoriënteerd Programmeren: WPO 1 1. Inhoud Opfrissing syntax, programmeermethodes, datatypes, functies/procedures, tekenen in C#. Herhaling Informatica 1 ste bachelor. 2. Oefeningen Demo 1: Volume
Informatica: C# WPO 8
 Informatica: C# WPO 8 1. Inhoud Procedures (functies zonder return-waarde) 2. Oefeningen Demo 1: Teken driehoeken Demo 2: Print array of double A: Stapel blokken A: Weerstanden 1 A: Weerstanden 2 A: Draw
Informatica: C# WPO 8 1. Inhoud Procedures (functies zonder return-waarde) 2. Oefeningen Demo 1: Teken driehoeken Demo 2: Print array of double A: Stapel blokken A: Weerstanden 1 A: Weerstanden 2 A: Draw
Informatica: C# WPO 6
 Informatica: C# WPO 6 1. Inhoud Timers, switch cases, combobox 2. Oefeningen Demo 1: Bounce Demo 2: Hex to decimal converter Demo 3: Debug oplossing demo 1 A: Count to 10 A: Biljarttafel A: To reverse
Informatica: C# WPO 6 1. Inhoud Timers, switch cases, combobox 2. Oefeningen Demo 1: Bounce Demo 2: Hex to decimal converter Demo 3: Debug oplossing demo 1 A: Count to 10 A: Biljarttafel A: To reverse
Informatica: C# WPO 2
 Informatica: C# WPO 2 1. Inhoud If, globale variabelen, debuggen, randomgetallen, strings vergelijken 2. Oefeningen Demo 1: Deelbaar door 0 Demo 2: Kassa Demo 3: Debug oplossingen demo s 1 en 2 A: Verschillend
Informatica: C# WPO 2 1. Inhoud If, globale variabelen, debuggen, randomgetallen, strings vergelijken 2. Oefeningen Demo 1: Deelbaar door 0 Demo 2: Kassa Demo 3: Debug oplossingen demo s 1 en 2 A: Verschillend
Informatica: C# WPO 6
 Informatica: C# WPO 6 1. Inhoud Timers, switch cases, combobox 2. Oefeningen Demo 1: Bounce Demo 2: Hex to decimal converter Demo 3: Debug oplossing demo 1 A: Count to 10 A: Biljarttafel A: Azerty to qwerty
Informatica: C# WPO 6 1. Inhoud Timers, switch cases, combobox 2. Oefeningen Demo 1: Bounce Demo 2: Hex to decimal converter Demo 3: Debug oplossing demo 1 A: Count to 10 A: Biljarttafel A: Azerty to qwerty
Informatica: C# WPO 13
 Informatica: C# WPO 13 1. Inhoud Bestanden uitlezen, bestanden schrijven en data toevoegen aan een bestand, csv-bestanden 2. Oefeningen Demo 1: Notepad Demo 2: Read CSV-file Demo 3: Write CSV-file A: Plot
Informatica: C# WPO 13 1. Inhoud Bestanden uitlezen, bestanden schrijven en data toevoegen aan een bestand, csv-bestanden 2. Oefeningen Demo 1: Notepad Demo 2: Read CSV-file Demo 3: Write CSV-file A: Plot
Informatica: C# WPO 12
 Informatica: C# WPO 12 1. Inhoud Datacontainers, bestanden uitlezen, bestanden schrijven en data toevoegen aan en bestand, csv-bestanden 2. Oefeningen Demo 1: Point2D Demo 2: Notepad Demo 3: Read CSV-file
Informatica: C# WPO 12 1. Inhoud Datacontainers, bestanden uitlezen, bestanden schrijven en data toevoegen aan en bestand, csv-bestanden 2. Oefeningen Demo 1: Point2D Demo 2: Notepad Demo 3: Read CSV-file
Informatica: C# WPO 7
 Informatica: C# WPO 7 1. Inhoud 1D-arrays, Lijsten 2. Oefeningen Demo 1: Vul de 1D-array Demo 2: Stringreplace Demo 3: Vul de lijst Demo 4: Debug oplossingen demo s 1, 2 en 3 A: Array reversal A: Gemiddelde
Informatica: C# WPO 7 1. Inhoud 1D-arrays, Lijsten 2. Oefeningen Demo 1: Vul de 1D-array Demo 2: Stringreplace Demo 3: Vul de lijst Demo 4: Debug oplossingen demo s 1, 2 en 3 A: Array reversal A: Gemiddelde
2010-I. A heeft de coördinaten (4 a, 4a a 2 ). Vraag 1. Toon dit aan. Gelijkstellen: y= 4x x 2 A. y= ax
 00-I De parabool met vergelijking y = 4x x en de x-as sluiten een vlakdeel V in. De lijn y = ax (met 0 a < 4) snijdt de parabool in de oorsprong en in punt. Zie de figuur. y= 4x x y= ax heeft de coördinaten
00-I De parabool met vergelijking y = 4x x en de x-as sluiten een vlakdeel V in. De lijn y = ax (met 0 a < 4) snijdt de parabool in de oorsprong en in punt. Zie de figuur. y= 4x x y= ax heeft de coördinaten
Riemannsommen en integralen
 Riemannsommen en integralen MET DE TI-NSPIRE Vervangt een deel van 0. uit VWO B deel gghm EEBII 0-0 Inhoud Oppervlakte onder de grafiek... Ondersom... 4 Bovensom... 4 Middensom... 4 Riemannsom... 5 Riemannsom
Riemannsommen en integralen MET DE TI-NSPIRE Vervangt een deel van 0. uit VWO B deel gghm EEBII 0-0 Inhoud Oppervlakte onder de grafiek... Ondersom... 4 Bovensom... 4 Middensom... 4 Riemannsom... 5 Riemannsom
Eindexamen wiskunde B vwo 2010 - I
 Gelijke oppervlakten De parabool met vergelijking y = 4x x2 en de x-as sluiten een vlakdeel V in. De lijn y = ax (met 0 a < 4) snijdt de parabool in de oorsprong O en in punt. Zie. y 4 3 2 1-1 O 1 2 3
Gelijke oppervlakten De parabool met vergelijking y = 4x x2 en de x-as sluiten een vlakdeel V in. De lijn y = ax (met 0 a < 4) snijdt de parabool in de oorsprong O en in punt. Zie. y 4 3 2 1-1 O 1 2 3
Graphics. Small Basic graphics 1/6
 Small Basic graphics 1/6 Graphics Naast het werken met tekst kan je in Small Basic ook werken met grafische elementen: lijnen, vormen en kleuren. Hierbij gebruik je het grafische venster met de witte achtergrond.
Small Basic graphics 1/6 Graphics Naast het werken met tekst kan je in Small Basic ook werken met grafische elementen: lijnen, vormen en kleuren. Hierbij gebruik je het grafische venster met de witte achtergrond.
Informatica: C# WPO 10
 Informatica: C# WPO 10 1. Inhoud 2D arrays, lijsten van arrays, NULL-values 2. Oefeningen Demo 1: Fill and print 2D array Demo 2: Fill and print list of array A: Matrix optelling A: Matrix * constante
Informatica: C# WPO 10 1. Inhoud 2D arrays, lijsten van arrays, NULL-values 2. Oefeningen Demo 1: Fill and print 2D array Demo 2: Fill and print list of array A: Matrix optelling A: Matrix * constante
Informatica: C# WPO 9
 Informatica: C# WPO 9 1. Inhoud Functies (functies met return-waarde) 2. Oefeningen Demo 1: Som Demo 2: Min en max of array Demo 3: Retourneer array van randomwaarden A: Absolute waarde A: Afstand A: Aantrekkingskracht
Informatica: C# WPO 9 1. Inhoud Functies (functies met return-waarde) 2. Oefeningen Demo 1: Som Demo 2: Min en max of array Demo 3: Retourneer array van randomwaarden A: Absolute waarde A: Afstand A: Aantrekkingskracht
OEFENINGEN PYTHON REEKS 4
 Vraag 1: Introductie Tekenen OEFENINGEN PYTHON REEKS 4 Vanaf deze les gaan we gebruik maken van het pakket VPython om de objecten te tekenen en weer te geven. Om aan alle functies te kunnen die VPython
Vraag 1: Introductie Tekenen OEFENINGEN PYTHON REEKS 4 Vanaf deze les gaan we gebruik maken van het pakket VPython om de objecten te tekenen en weer te geven. Om aan alle functies te kunnen die VPython
Inhoud van een omwentelingslichaam
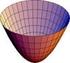 Inhoud van een omwentelingslichaam Wat is een omwentelingslichaam? Omwentelingslichamen ontstaan door het wentelen van een vlakdeel rond een rechte: de omwentelingsas Voorbeeld: volume van een (omwentelings)cilinder
Inhoud van een omwentelingslichaam Wat is een omwentelingslichaam? Omwentelingslichamen ontstaan door het wentelen van een vlakdeel rond een rechte: de omwentelingsas Voorbeeld: volume van een (omwentelings)cilinder
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: goniometrie en meetkunde. 22 juli 2015. dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: goniometrie en meetkunde 22 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: goniometrie en meetkunde 22 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Examen HAVO. wiskunde B1,2. tijdvak 2 woensdag 18 juni 13.30-16.30. Bij dit examen hoort een uitwerkbijlage.
 Examen HAVO 008 tijdvak woensdag 18 juni 13.30-16.30 wiskunde B1, Bij dit examen hoort een uitwerkbijlage. it examen bestaat uit 18 vragen. Voor dit examen zijn maximaal 81 punten te behalen. Voor elk
Examen HAVO 008 tijdvak woensdag 18 juni 13.30-16.30 wiskunde B1, Bij dit examen hoort een uitwerkbijlage. it examen bestaat uit 18 vragen. Voor dit examen zijn maximaal 81 punten te behalen. Voor elk
Examen VWO. wiskunde B. tijdvak 1 dinsdag 25 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Examen VWO 2010 tijdvak 1 dinsdag 25 mei 13.30-16.30 uur wiskunde B Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 18 vragen. Voor dit examen zijn maximaal 84 punten te behalen. Voor elk
Examen VWO 2010 tijdvak 1 dinsdag 25 mei 13.30-16.30 uur wiskunde B Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 18 vragen. Voor dit examen zijn maximaal 84 punten te behalen. Voor elk
Examen VMBO-KB. wiskunde CSE KB. tijdvak 1 dinsdag 15 mei uur. Bij dit examen hoort een uitwerkbijlage.
 Examen VMBO-KB 2018 tijdvak 1 dinsdag 15 mei 13.30-15.30 uur wiskunde CSE KB Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 26 vragen. Voor dit examen zijn maximaal 74 punten te behalen.
Examen VMBO-KB 2018 tijdvak 1 dinsdag 15 mei 13.30-15.30 uur wiskunde CSE KB Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 26 vragen. Voor dit examen zijn maximaal 74 punten te behalen.
Examen VWO. wiskunde B1 (nieuwe stijl)
 wiskunde B1 (nieuwe stijl) Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei 13.30 16.30 uur 20 04 Voor dit examen zijn maximaal 86 punten te behalen; het examen bestaat uit
wiskunde B1 (nieuwe stijl) Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei 13.30 16.30 uur 20 04 Voor dit examen zijn maximaal 86 punten te behalen; het examen bestaat uit
Homogene groepen, de balk
 Volgende week mag je zelf een les van ongeveer 20 minuten geven aan je medeleerlingen over de balk, cilinder of kegel. Een goede les bevat veel leerlingactiviteit. Zorg er dus voor dat je je leerlingen
Volgende week mag je zelf een les van ongeveer 20 minuten geven aan je medeleerlingen over de balk, cilinder of kegel. Een goede les bevat veel leerlingactiviteit. Zorg er dus voor dat je je leerlingen
Examen HAVO en VHBO. Wiskunde B
 Wiskunde B Examen HAVO en VHBO Hoger Algemeen Voortgezet Onderwijs Vooropleiding Hoger Beroeps Onderwijs HAVO Tijdvak 1 VHBO Tijdvak 2 Dinsdag 23 mei 13.30 16.30 uur 00 Dit examen bestaat uit 19 vragen.
Wiskunde B Examen HAVO en VHBO Hoger Algemeen Voortgezet Onderwijs Vooropleiding Hoger Beroeps Onderwijs HAVO Tijdvak 1 VHBO Tijdvak 2 Dinsdag 23 mei 13.30 16.30 uur 00 Dit examen bestaat uit 19 vragen.
Eindexamen wiskunde B1 vwo 2004-I
 Machten van een derdegraadsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. 4p 1 Toon algebraïsch aan dat het maximum van f gelijk is aan 1. V is het gebied ingesloten door de
Machten van een derdegraadsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. 4p 1 Toon algebraïsch aan dat het maximum van f gelijk is aan 1. V is het gebied ingesloten door de
Eindexamen wiskunde B1-2 havo 2008-II
 Koffiekan Bij het zetten van koffie wordt soms een koffiezetapparaat gebruikt. eze opgave gaat over een koffiezetapparaat waarbij de koffiekan, zonder het handvat en de bovenrand, de vorm heeft van een
Koffiekan Bij het zetten van koffie wordt soms een koffiezetapparaat gebruikt. eze opgave gaat over een koffiezetapparaat waarbij de koffiekan, zonder het handvat en de bovenrand, de vorm heeft van een
Eindexamen wiskunde B havo I (oude stijl)
 Een functie Voor 0 < = x < = 2π is gegeven de functie figuur 1 f(x) = 2sin(x + 1 6 π). In figuur 1 is de grafiek van f getekend. y 1 f 4 p 1 Los op: f(x) < 1. De lijn l raakt de grafiek van f in het punt
Een functie Voor 0 < = x < = 2π is gegeven de functie figuur 1 f(x) = 2sin(x + 1 6 π). In figuur 1 is de grafiek van f getekend. y 1 f 4 p 1 Los op: f(x) < 1. De lijn l raakt de grafiek van f in het punt
6.0 Voorkennis AD BC. Kruislings vermenigvuldigen: Voorbeeld: 50 10x. 50 10( x 1) Willem-Jan van der Zanden
 6.0 Voorkennis Kruislings vermenigvuldigen: A C AD BC B D Voorbeeld: 50 0 x 50 0( x ) 50 0x 0 0x 60 x 6 6.0 Voorkennis Herhaling van rekenregels voor machten: p p q pq a pq a a a [] a [2] q a q p pq p
6.0 Voorkennis Kruislings vermenigvuldigen: A C AD BC B D Voorbeeld: 50 0 x 50 0( x ) 50 0x 0 0x 60 x 6 6.0 Voorkennis Herhaling van rekenregels voor machten: p p q pq a pq a a a [] a [2] q a q p pq p
0. voorkennis. Periodieke verbanden. Bijzonder rechthoekige driehoeken en goniometrische verhoudingen
 0. voorkennis Periodieke verbanden Bijzonder rechthoekige driehoeken en goniometrische verhoudingen Er zijn twee verschillende tekendriehoeken: de 45-45 -90 driehoek en de 30-0 -90 -driehoek. Kenmerken
0. voorkennis Periodieke verbanden Bijzonder rechthoekige driehoeken en goniometrische verhoudingen Er zijn twee verschillende tekendriehoeken: de 45-45 -90 driehoek en de 30-0 -90 -driehoek. Kenmerken
15 a De rechthoeken zijn 1 bij 6 lucifers, of 2 bij 5 lucifers, of 3 bij 4 lucifers. Zie figuur: Hoofdstuk 21 OPPERVLAKTE HAVO 21.
 Hoofdstuk 1 OPPERVLAKTE HAVO 1.1 INTRO 15 a De rechthoeken zijn 1 bij 6 lucifers, of bij 5 lucifers, of 3 bij 4 lucifers. Zie figuur: 1 Oppervlakte snelweg = 0 km 18 m = 0.000 m 18 m = 360.000 m. Zijde
Hoofdstuk 1 OPPERVLAKTE HAVO 1.1 INTRO 15 a De rechthoeken zijn 1 bij 6 lucifers, of bij 5 lucifers, of 3 bij 4 lucifers. Zie figuur: 1 Oppervlakte snelweg = 0 km 18 m = 0.000 m 18 m = 360.000 m. Zijde
Examen VWO. Wiskunde B Profi
 Wiskunde B Profi Eamen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Donderdag 25 mei 3.30 6.30 uur 20 00 Dit eamen bestaat uit 7 vragen. Voor elk vraagnummer is aangegeven hoeveel punten met een
Wiskunde B Profi Eamen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Donderdag 25 mei 3.30 6.30 uur 20 00 Dit eamen bestaat uit 7 vragen. Voor elk vraagnummer is aangegeven hoeveel punten met een
16 a. b a. b 6a. de Wageningse Methode Antwoorden H21 OPPERVLAKTE HAVO 1
 Hoofdstuk OPPERVLAKTE HAVO 5 a De rechthoeken zijn bij 6 lucifers, of bij 5 lucifers, of 3 bij 4 lucifers.. INTRO Oppervlakte snelweg = 0 km 8 m = 0.000 m 8 m = 360.000 m. Zijde vierkant = 360. 000 = 600
Hoofdstuk OPPERVLAKTE HAVO 5 a De rechthoeken zijn bij 6 lucifers, of bij 5 lucifers, of 3 bij 4 lucifers.. INTRO Oppervlakte snelweg = 0 km 8 m = 0.000 m 8 m = 360.000 m. Zijde vierkant = 360. 000 = 600
werkschrift passen en meten
 werkschrift passen en meten 1 vierhoeken 2 De vijf in één - puzzel 7 Een puzzel De serie spiegelsymmetrische figuren is volgens een bepaald systeem opgebouwd. Teken de volgende figuren in de reeks. 8 Een
werkschrift passen en meten 1 vierhoeken 2 De vijf in één - puzzel 7 Een puzzel De serie spiegelsymmetrische figuren is volgens een bepaald systeem opgebouwd. Teken de volgende figuren in de reeks. 8 Een
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig.
 7 Totaalbeeld Samenvatten Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig. Begrippenlijst: 21: functie invoerwaarde
7 Totaalbeeld Samenvatten Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig. Begrippenlijst: 21: functie invoerwaarde
De grafiek van een lineair verband is altijd een rechte lijn.
 Verbanden Als er tussen twee variabelen x en y een verband bestaat kunnen we dat op meerdere manieren vastleggen: door een vergelijking, door een grafiek of door een tabel. Stel dat het verband tussen
Verbanden Als er tussen twee variabelen x en y een verband bestaat kunnen we dat op meerdere manieren vastleggen: door een vergelijking, door een grafiek of door een tabel. Stel dat het verband tussen
Labo 2 Programmeren II
 Labo 2 Programmeren II L. Schoofs K. van Assche Gebruik Visual Studio 2005 om een programma te ontwikkelen dat eenvoudige grafieken tekent. Deze opgave heb je vorig academiejaar reeds in Java geïmplementeerd.
Labo 2 Programmeren II L. Schoofs K. van Assche Gebruik Visual Studio 2005 om een programma te ontwikkelen dat eenvoudige grafieken tekent. Deze opgave heb je vorig academiejaar reeds in Java geïmplementeerd.
Wiskunde Vraag 1. Vraag 2. Vraag 3. Vraag 4 21/12/2008
 Wiskunde 007- //008 Vraag Veronderstel dat de concentraties in het bloed van stof A en van stof B omgekeerd evenredig zijn en positief. Als de concentratie van stof A met p % toeneemt, dan zal de concentratie
Wiskunde 007- //008 Vraag Veronderstel dat de concentraties in het bloed van stof A en van stof B omgekeerd evenredig zijn en positief. Als de concentratie van stof A met p % toeneemt, dan zal de concentratie
Meetkunde. MBO Wiskunde Niveau 4 - Leerjaar 1, periode 3
 Meetkunde MBO Wiskunde Niveau 4 - Leerjaar 1, periode 3 LOCATIE: Noorderpoort Beroepsonderwijs Stadskanaal DOMEINEN: Bouwkunde, Werktuigbouw, Research Instrumentmaker LEERWEG: BOL - MBO Niveau 4 DATUM:
Meetkunde MBO Wiskunde Niveau 4 - Leerjaar 1, periode 3 LOCATIE: Noorderpoort Beroepsonderwijs Stadskanaal DOMEINEN: Bouwkunde, Werktuigbouw, Research Instrumentmaker LEERWEG: BOL - MBO Niveau 4 DATUM:
vwo wiskunde b Baanversnelling de Wageningse Methode
 1 1 vwo wiskunde b Baanversnelling de Wageningse Methode 1 1 2 2 Copyright 2018 Stichting de Wageningse Methode Auteurs Leon van den Broek, Ton Geurtz, Maris van Haandel, Erik van Haren, Dolf van den Hombergh,
1 1 vwo wiskunde b Baanversnelling de Wageningse Methode 1 1 2 2 Copyright 2018 Stichting de Wageningse Methode Auteurs Leon van den Broek, Ton Geurtz, Maris van Haandel, Erik van Haren, Dolf van den Hombergh,
De grafiek van een lineair verband is altijd een rechte lijn.
 2. Verbanden Verbanden Als er tussen twee variabelen x en y een verband bestaat kunnen we dat op meerdere manieren vastleggen: door een vergelijking, door een grafiek of door een tabel. Stel dat het verband
2. Verbanden Verbanden Als er tussen twee variabelen x en y een verband bestaat kunnen we dat op meerdere manieren vastleggen: door een vergelijking, door een grafiek of door een tabel. Stel dat het verband
Eindexamen wiskunde B1-2 vwo 2007-II
 ier tappen ij het tappen van bier treden verschillen op in de hoeveelheid bier per glas. Uit onderzoek blijkt dat de hoeveelheid bier die per glas getapt wordt bij benadering normaal verdeeld is met een
ier tappen ij het tappen van bier treden verschillen op in de hoeveelheid bier per glas. Uit onderzoek blijkt dat de hoeveelheid bier die per glas getapt wordt bij benadering normaal verdeeld is met een
OPLOSSINGEN. Wallabie Vlaamse Wiskunde Olympiade vzw
 OPLOSSINGEN Vlaamse Wiskunde Olympiade vzw Juist antwoord Geen antwoord Fout antwoord Wedstrijdduur Rekentoestel 5 punten 1 punt 0 punten 75 minuten niet toegelaten 1. Correct antwoord: A Alswegewoondeurenoptellen,vindenwe:17+17=34.Hetisdus34uur,
OPLOSSINGEN Vlaamse Wiskunde Olympiade vzw Juist antwoord Geen antwoord Fout antwoord Wedstrijdduur Rekentoestel 5 punten 1 punt 0 punten 75 minuten niet toegelaten 1. Correct antwoord: A Alswegewoondeurenoptellen,vindenwe:17+17=34.Hetisdus34uur,
Examen HAVO 2013. wiskunde B. tijdvak 1 vrijdag 17 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Examen HAVO 201 tijdvak 1 vrijdag 17 mei 1.0-16.0 uur wiskunde B Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 19 vragen. Voor dit examen zijn maximaal 80 punten te behalen. Voor elk
Examen HAVO 201 tijdvak 1 vrijdag 17 mei 1.0-16.0 uur wiskunde B Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 19 vragen. Voor dit examen zijn maximaal 80 punten te behalen. Voor elk
Aanvullende tekst bij hoofdstuk 1
 Aanvullende tekst bij hoofdstuk 1 Wortels uit willekeurige getallen In paragraaf 1.3.5 hebben we het worteltrekalgoritme besproken. Dat deden we aan de hand van de relatie tussen de (van tevoren gegeven)
Aanvullende tekst bij hoofdstuk 1 Wortels uit willekeurige getallen In paragraaf 1.3.5 hebben we het worteltrekalgoritme besproken. Dat deden we aan de hand van de relatie tussen de (van tevoren gegeven)
Beweging. De beginvoorwaarden voor het numerieke programma zijn als volgt: x(0) = 0 m y(0) = 2,0 m. Plaats: vx(0) = 4,0 m/s vy(0) = 0 m/s.
 Beweging Voorbeeld: Roofjump II Bij één van de voorgaande opgaven heb je moeten berekenen hoe snel iemand moet rennen om van een hoger gelegen dak naar een lager gelegen dak te springen. In het eenvoudige
Beweging Voorbeeld: Roofjump II Bij één van de voorgaande opgaven heb je moeten berekenen hoe snel iemand moet rennen om van een hoger gelegen dak naar een lager gelegen dak te springen. In het eenvoudige
Projectietekenen is een hulpmiddel om een beter en sneller inzicht te krijgen in een product.
 1 Projectietekenen 1.1 Inleiding Projectietekenen is een hulpmiddel om een beter en sneller inzicht te krijgen in een product. Gebouwen, gevelelementen, kozijnen en betimmeringen zijn voorwerpen met een
1 Projectietekenen 1.1 Inleiding Projectietekenen is een hulpmiddel om een beter en sneller inzicht te krijgen in een product. Gebouwen, gevelelementen, kozijnen en betimmeringen zijn voorwerpen met een
TOELATINGSEXAMEN ANALYSE BURGERLIJK INGENIEUR EN BURGERLIJK INGENIEUR ARCHTECT - 3 JULI 2003 BLZ 1/8
 BURGERLIJK INGENIEUR ARCHTECT - 3 JULI 2003 BLZ 1/8 1. De functie f(x) = e kx + ax + b met a, b en k R en k < 0 heeft een schuine asymptoot y = x voor x + en voldoet aan de vergelijking Bepaal a, b en
BURGERLIJK INGENIEUR ARCHTECT - 3 JULI 2003 BLZ 1/8 1. De functie f(x) = e kx + ax + b met a, b en k R en k < 0 heeft een schuine asymptoot y = x voor x + en voldoet aan de vergelijking Bepaal a, b en
ZESDE KLAS MEETKUNDE
 ZESDE KLAS MEETKUNDE maandag 1. Het vierkant. Eigenschappen. 2. Vierkanten tekenen met passer en lat vanuit zeshoek 3. Vierkanten tekenen met passer en lat binnen cirkel 4. Vierkanten tekenen met passer
ZESDE KLAS MEETKUNDE maandag 1. Het vierkant. Eigenschappen. 2. Vierkanten tekenen met passer en lat vanuit zeshoek 3. Vierkanten tekenen met passer en lat binnen cirkel 4. Vierkanten tekenen met passer
Informatica: C# WPO 11
 Informatica: C# WPO 11 1. Inhoud Pass by reference (ref, out), recursie, code opdelen in verschillende codebestanden 2. Oefeningen Demo 1: Swapfunctie Demo 2: TryParse(int) Demo 3: Recursion Tree Demo
Informatica: C# WPO 11 1. Inhoud Pass by reference (ref, out), recursie, code opdelen in verschillende codebestanden 2. Oefeningen Demo 1: Swapfunctie Demo 2: TryParse(int) Demo 3: Recursion Tree Demo
Oefenexamen wiskunde vmbo-tl Onderwerp: meetkunde H2 H6 H8 Antwoorden: achterin dit boekje
 Oefenexamen wiskunde vmbo-tl Onderwerp: meetkunde H2 H6 H8 Antwoorden: achterin dit boekje Indien van toepassing: schrijf je berekening op. Tekening altijd met geodriehoek en potlood. Omtrek rechthoek
Oefenexamen wiskunde vmbo-tl Onderwerp: meetkunde H2 H6 H8 Antwoorden: achterin dit boekje Indien van toepassing: schrijf je berekening op. Tekening altijd met geodriehoek en potlood. Omtrek rechthoek
Examen VWO. wiskunde B1. tijdvak 2 woensdag 18 juni uur
 Eamen VWO 008 tijdvak woensdag 18 juni 13.30-16.30 uur wiskunde B1 Dit eamen bestaat uit 18 vragen. Voor dit eamen zijn maimaal 84 punten te behalen. Voor elk vraagnummer staat hoeveel punten met een goed
Eamen VWO 008 tijdvak woensdag 18 juni 13.30-16.30 uur wiskunde B1 Dit eamen bestaat uit 18 vragen. Voor dit eamen zijn maimaal 84 punten te behalen. Voor elk vraagnummer staat hoeveel punten met een goed
d = 8 cm 2 6 A: = 26 m 2 B: = 20 m 2 C: = 18 m 2 D: 20 m 2 E: 26 m 2
 H17 PYTHAGORAS 17.1 INTRO 1 b c d 1 4 4 = 8 cm 6 A: 6 1 5 1 4 = 6 m B: 6 1 4 4 = 0 m C: 6 1 3 3 4 = 18 m D: 0 m E: 6 m 7 a A:, cm B: 5,0 cm C: 3, cm D: 4,1 cm b Voor elke zijde geldt dat het de schuine
H17 PYTHAGORAS 17.1 INTRO 1 b c d 1 4 4 = 8 cm 6 A: 6 1 5 1 4 = 6 m B: 6 1 4 4 = 0 m C: 6 1 3 3 4 = 18 m D: 0 m E: 6 m 7 a A:, cm B: 5,0 cm C: 3, cm D: 4,1 cm b Voor elke zijde geldt dat het de schuine
In een zware tornado worden maximale windsnelheden van ongeveer 280 km/u bereikt.
 Tornadoschalen In tornado s kunnen hoge windsnelheden bereikt worden. De zwaarte of heftigheid van een tornado wordt intensiteit genoemd. Er zijn verschillende schalen om de intensiteit van een tornado
Tornadoschalen In tornado s kunnen hoge windsnelheden bereikt worden. De zwaarte of heftigheid van een tornado wordt intensiteit genoemd. Er zijn verschillende schalen om de intensiteit van een tornado
5.1 Lineaire formules [1]
![5.1 Lineaire formules [1] 5.1 Lineaire formules [1]](/thumbs/40/21464476.jpg) 5.1 Lineaire formules [1] Voorbeeld : Teken de grafiek van y = 1½x - 3 Stap 1: Maak een tabel met twee coördinaten van deze lijn: x 0 2 y -3 0 Stap 2: Teken de twee punten en de grafiek: 1 5.1 Lineaire
5.1 Lineaire formules [1] Voorbeeld : Teken de grafiek van y = 1½x - 3 Stap 1: Maak een tabel met twee coördinaten van deze lijn: x 0 2 y -3 0 Stap 2: Teken de twee punten en de grafiek: 1 5.1 Lineaire
Trillingen en geluid wiskundig. 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude 1 De sinus van een hoek Eenheidscirkel In de figuur hiernaast
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude 1 De sinus van een hoek Eenheidscirkel In de figuur hiernaast
X. Grafische elementen
 X. Grafische elementen Om u te helpen bij grafische voorstellingen heeft java een aantal grafische afbeeldingen die u kunt gebruiken. Meestal worden zij in de methode paint(graphics g) geplaatst. Zij moeten
X. Grafische elementen Om u te helpen bij grafische voorstellingen heeft java een aantal grafische afbeeldingen die u kunt gebruiken. Meestal worden zij in de methode paint(graphics g) geplaatst. Zij moeten
P is nu het punt waarvan de x-coördinaat gelijk is aan die van het punt X en waarvan de y-coördinaat gelijk is aan AB (inclusief het teken).
 Inhoud 1. Sinus-functie 1 2. Cosinus-functie 3 3. Tangens-functie 5 4. Eigenschappen 4.1. Verband tussen goniometrische verhoudingen en goniometrische functies 8 4.2. Enkele eigenschappen van de sinus-functie
Inhoud 1. Sinus-functie 1 2. Cosinus-functie 3 3. Tangens-functie 5 4. Eigenschappen 4.1. Verband tussen goniometrische verhoudingen en goniometrische functies 8 4.2. Enkele eigenschappen van de sinus-functie
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 18 mei uur
 Eamen VW 016 tijdvak 1 woensdag 18 mei 13.30-16.30 uur wiskunde (pilot) it eamen bestaat uit 16 vragen. Voor dit eamen zijn maimaal 79 punten te behalen. Voor elk vraagnummer staat hoeveel punten met een
Eamen VW 016 tijdvak 1 woensdag 18 mei 13.30-16.30 uur wiskunde (pilot) it eamen bestaat uit 16 vragen. Voor dit eamen zijn maimaal 79 punten te behalen. Voor elk vraagnummer staat hoeveel punten met een
Luc Gheysens - Extremumvraagstukken p.1
 EXTREMUMVRAAGSTUKKEN 1 Bepaal twee getallen x en y waarvan de som 144 is en waarvoor het product maximaal is. En voor welke waarden is het product x 3. y 2 maximaal? 2 Aan de vier hoeken van een vierkantig
EXTREMUMVRAAGSTUKKEN 1 Bepaal twee getallen x en y waarvan de som 144 is en waarvoor het product maximaal is. En voor welke waarden is het product x 3. y 2 maximaal? 2 Aan de vier hoeken van een vierkantig
Examen VWO. wiskunde B1,2. tijdvak 2 woensdag 20 juni uur. Bij dit examen hoort een uitwerkbijlage.
 Eamen VW 007 tijdvak woensdag 0 juni 13.30-16.30 uur wiskunde 1, ij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 17 vragen. Voor dit eamen zijn maimaal 81 punten te behalen. Voor elk vraagnummer
Eamen VW 007 tijdvak woensdag 0 juni 13.30-16.30 uur wiskunde 1, ij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 17 vragen. Voor dit eamen zijn maimaal 81 punten te behalen. Voor elk vraagnummer
Eindexamen wiskunde B havo II
 Opgave 1 Een functie e functie f is gegeven door figuur 1 2x 40 f (x) =, waarbij x 19. x 19 In figuur 1 en op de bijlage is de grafiek getekend van f en de verticale asymptoot x = 19. 6p 1 Los op: 0
Opgave 1 Een functie e functie f is gegeven door figuur 1 2x 40 f (x) =, waarbij x 19. x 19 In figuur 1 en op de bijlage is de grafiek getekend van f en de verticale asymptoot x = 19. 6p 1 Los op: 0
OEFENINGEN PYTHON REEKS 5
 Vraag 1: Interpoleren (vervolg) OEFENINGEN PYTHON REEKS 5 Bouw verder op je code van Reeks 3, vraag 4. Voeg vier constanten toe aan je code: X0 = 280, Y0 = 0, Z0 = 50 en SIZE = 8. a) Teken een kubus met
Vraag 1: Interpoleren (vervolg) OEFENINGEN PYTHON REEKS 5 Bouw verder op je code van Reeks 3, vraag 4. Voeg vier constanten toe aan je code: X0 = 280, Y0 = 0, Z0 = 50 en SIZE = 8. a) Teken een kubus met
Datum. Vraag het bedrag in BEF. Reken om naar EURO. Toon het bedrag in EURO. --- Vraag het bedrag in BEF--- --- Reken om naar EURO---
 3UREOHPHQRSORVVHQPHW9%$WRHSDVVLQJHQELMGHHO Naam. NR : Klas. PC : Datum. 23*$9( Hieronder vind je het algoritme om een bedrag in BEF om te rekenen naar EURO. Zet het algoritme om in programmacode. Noem
3UREOHPHQRSORVVHQPHW9%$WRHSDVVLQJHQELMGHHO Naam. NR : Klas. PC : Datum. 23*$9( Hieronder vind je het algoritme om een bedrag in BEF om te rekenen naar EURO. Zet het algoritme om in programmacode. Noem
Examen HAVO. wiskunde B1,2. tijdvak 1 dinsdag 20 mei uur
 Examen HAVO 2008 tijdvak 1 dinsdag 20 mei 13.30-16.30 uur wiskunde B1,2 Dit examen bestaat uit 18 vragen. Voor dit examen zijn maximaal 83 punten te behalen. Voor elk vraagnummer staat hoeveel punten met
Examen HAVO 2008 tijdvak 1 dinsdag 20 mei 13.30-16.30 uur wiskunde B1,2 Dit examen bestaat uit 18 vragen. Voor dit examen zijn maximaal 83 punten te behalen. Voor elk vraagnummer staat hoeveel punten met
Examen VMBO-GL en TL. wiskunde CSE GL en TL. tijdvak 2 dinsdag 21 juni uur. Bij dit examen hoort een uitwerkbijlage.
 Examen VMBO-GL en TL 2011 tijdvak 2 dinsdag 21 juni 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 25 vragen. Voor dit examen zijn maximaal 75 punten
Examen VMBO-GL en TL 2011 tijdvak 2 dinsdag 21 juni 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 25 vragen. Voor dit examen zijn maximaal 75 punten
Instructie voor Docenten. Hoofdstuk 13 OMTREK EN OPPERVLAKTE
 Instructie voor Docenten Hoofdstuk 13 OMTREK EN OPPERVLAKTE Instructie voor docenten H13: OMTREK EN OPPERVLAKTE DOELEN VAN DIT HOOFDSTUK: Leerlingen weten wat de begrippen omtrek en oppervlakte betekenen.
Instructie voor Docenten Hoofdstuk 13 OMTREK EN OPPERVLAKTE Instructie voor docenten H13: OMTREK EN OPPERVLAKTE DOELEN VAN DIT HOOFDSTUK: Leerlingen weten wat de begrippen omtrek en oppervlakte betekenen.
Opvouwbare kubus (180 o )
 Workshop Verpakkingen NWD 18 februari 2012 hm / rvo Opvouwbare kubus (180 o ) - Een bouwplaat van de kubus en een voorbeeldfoto - Als je een mooi wilt maken: een A4-tje 160 g wit papier en een schutblad,
Workshop Verpakkingen NWD 18 februari 2012 hm / rvo Opvouwbare kubus (180 o ) - Een bouwplaat van de kubus en een voorbeeldfoto - Als je een mooi wilt maken: een A4-tje 160 g wit papier en een schutblad,
Op groot blad papier (verticaal of op plat vlak)
 OEFENING: TEKENEN IN SYMMETRIE MET BEIDE HANDEN GELIJKTIJDIG Op bord (verticaal) Op groot blad papier (verticaal of op plat vlak) L R L R Ik zie het anders OEFENING: SYMMETRIE L R Oefeningen voor kinderen
OEFENING: TEKENEN IN SYMMETRIE MET BEIDE HANDEN GELIJKTIJDIG Op bord (verticaal) Op groot blad papier (verticaal of op plat vlak) L R L R Ik zie het anders OEFENING: SYMMETRIE L R Oefeningen voor kinderen
5,7. Profielwerkstuk door een scholier 2227 woorden 8 april keer beoordeeld. Wie was Pythagoras?
 Profielwerkstuk door een scholier 2227 woorden 8 april 2005 5,7 186 keer beoordeeld Vak Wiskunde Wie was Pythagoras? Pythagoras was een Griekse wijsgeer die rond 575 voor Christus leefde. Zijn vader was
Profielwerkstuk door een scholier 2227 woorden 8 april 2005 5,7 186 keer beoordeeld Vak Wiskunde Wie was Pythagoras? Pythagoras was een Griekse wijsgeer die rond 575 voor Christus leefde. Zijn vader was
INDITHOOFDSTUKgaan jullie kennismaken met het cartesisch assenstelsel.
 Hoofdstuk 5 Het Assenstelsel 5.1 Het Assenstelsel INDITHOOFDSTUKgaan jullie kennismaken met het cartesisch assenstelsel. Dit assenstelsel is een idee van de Franse filosoof en wiskundige René Descartes(1596-1650).
Hoofdstuk 5 Het Assenstelsel 5.1 Het Assenstelsel INDITHOOFDSTUKgaan jullie kennismaken met het cartesisch assenstelsel. Dit assenstelsel is een idee van de Franse filosoof en wiskundige René Descartes(1596-1650).
Eindexamen wiskunde B vwo 2010 - I
 Formules Vlakke meetkunde Verwijzingen naar definities en stellingen die bij een bewijs mogen worden gebruikt zonder nadere toelichting. Hoeken, lijnen en afstanden: gestrekte hoek, rechte hoek, overstaande
Formules Vlakke meetkunde Verwijzingen naar definities en stellingen die bij een bewijs mogen worden gebruikt zonder nadere toelichting. Hoeken, lijnen en afstanden: gestrekte hoek, rechte hoek, overstaande
Achter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen.
 Examen VMBO-GL en TL 2011 tijdvak 1 maandag 23 mei 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Achter het correctievoorschrift is een aanvulling op het correctievoorschrift
Examen VMBO-GL en TL 2011 tijdvak 1 maandag 23 mei 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Achter het correctievoorschrift is een aanvulling op het correctievoorschrift
Eindexamen vwo wiskunde B pilot 2013-I
 Eindeamen vwo wiskunde pilot 03-I Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin
Eindeamen vwo wiskunde pilot 03-I Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin
wiskunde CSE GL en TL
 Examen VMBO-GL en TL 2014 tijdvak 2 dinsdag 17 juni 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 23 vragen. Voor dit examen zijn maximaal 76 punten
Examen VMBO-GL en TL 2014 tijdvak 2 dinsdag 17 juni 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 23 vragen. Voor dit examen zijn maximaal 76 punten
Efficientie in de ruimte - leerlingmateriaal
 Junior College Utrecht Efficientie in de ruimte - leerlingmateriaal Versie 2 September 2012 Een project (ruimte-)meetkunde voor vwo-leerlingen Geschreven voor het Koningin Wilhelmina College Culemborg
Junior College Utrecht Efficientie in de ruimte - leerlingmateriaal Versie 2 September 2012 Een project (ruimte-)meetkunde voor vwo-leerlingen Geschreven voor het Koningin Wilhelmina College Culemborg
Eindexamen wiskunde B1-2 vwo 2008-II
 Eindeamen wiskunde B- vwo 008-II Een zwaartepunt Van een cirkelschijf met middelpunt (0, 0) en straal is het kwart getekend dat in het eerste kwadrant ligt. De cirkelboog is de grafiek van de functie f
Eindeamen wiskunde B- vwo 008-II Een zwaartepunt Van een cirkelschijf met middelpunt (0, 0) en straal is het kwart getekend dat in het eerste kwadrant ligt. De cirkelboog is de grafiek van de functie f
OEFENPROEFWERK VWO B DEEL 3
 Formules OEFENROEFWERK VWO B DEEL HOOFDSTUK GONIOMETRISCHE FORMULES cos( t u) cos( t)cos( u) sin( t)sin( u) sin( A) sin( A)cos( A) sin( t u) sin( t)cos( u) cos( t)sin( u) cos( t u) cos( t)cos( u) sin(
Formules OEFENROEFWERK VWO B DEEL HOOFDSTUK GONIOMETRISCHE FORMULES cos( t u) cos( t)cos( u) sin( t)sin( u) sin( A) sin( A)cos( A) sin( t u) sin( t)cos( u) cos( t)sin( u) cos( t u) cos( t)cos( u) sin(
HTML Graphics. Hans Roeyen V 3.0
 HTML Graphics Hans Roeyen V 3.0 19 maart 2015 Inhoud 1. HTML5 Canvas... 3 1.1. Het Canvas element... 3 2. SVG Element... 9 2.1. SVG vergeleken met Canvas... 9 2.2. Een cirkel tekenen met SVG... 10 2.2.1.
HTML Graphics Hans Roeyen V 3.0 19 maart 2015 Inhoud 1. HTML5 Canvas... 3 1.1. Het Canvas element... 3 2. SVG Element... 9 2.1. SVG vergeleken met Canvas... 9 2.2. Een cirkel tekenen met SVG... 10 2.2.1.
mailgroep photoshop Copyright
 http://psdtuts.com/tutorials/drawing/how-to-create-a-classic-guitar-from-scratch-in-photoshop/ Gitaar tekenen In deze les leer je een Klassieke Gitaar tekenen. Iedere vorm en effect wordt in Photoshop
http://psdtuts.com/tutorials/drawing/how-to-create-a-classic-guitar-from-scratch-in-photoshop/ Gitaar tekenen In deze les leer je een Klassieke Gitaar tekenen. Iedere vorm en effect wordt in Photoshop
Eindexamen vmbo gl/tl wiskunde 2011 - I
 OVERZICHT FORMULES: omtrek cirkel = diameter oppervlakte cirkel = straal 2 inhoud prisma = oppervlakte grondvlak hoogte inhoud cilinder = oppervlakte grondvlak hoogte inhoud kegel = 1 3 oppervlakte grondvlak
OVERZICHT FORMULES: omtrek cirkel = diameter oppervlakte cirkel = straal 2 inhoud prisma = oppervlakte grondvlak hoogte inhoud cilinder = oppervlakte grondvlak hoogte inhoud kegel = 1 3 oppervlakte grondvlak
Eindexamen wiskunde B1-2 vwo 2008-II
 Eindeamen wiskunde B- vwo 8-II Een zwaartepunt Van een cirkelschijf met middelpunt (, ) en straal is het kwart getekend dat in het eerste kwadrant ligt. De cirkelboog is de grafiek van de functie f die
Eindeamen wiskunde B- vwo 8-II Een zwaartepunt Van een cirkelschijf met middelpunt (, ) en straal is het kwart getekend dat in het eerste kwadrant ligt. De cirkelboog is de grafiek van de functie f die
Eindexamen wiskunde B1-2 havo 2008-I
 Steeds meer vlees In wordt voor de periode 1960-1996 zowel de graanproductie als de vleesproductie per hoofd van de wereldbevolking weergegeven. Hiervoor worden twee verticale assen gebruikt. De ronde
Steeds meer vlees In wordt voor de periode 1960-1996 zowel de graanproductie als de vleesproductie per hoofd van de wereldbevolking weergegeven. Hiervoor worden twee verticale assen gebruikt. De ronde
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 22 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Eamen VWO 203 tijdvak woensdag 22 mei 3.30-6.30 uur wiskunde B (pilot) Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 7 vragen. Voor dit eamen zijn maimaal 78 punten te behalen. Voor elk
Eamen VWO 203 tijdvak woensdag 22 mei 3.30-6.30 uur wiskunde B (pilot) Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 7 vragen. Voor dit eamen zijn maimaal 78 punten te behalen. Voor elk
Bij deze PTA-toets hoort een uitwerkbijlage, die behoort bij opdracht 4c. Pagina 1 van 8. Vestiging Westplasmavo
 Vestiging Westplasmavo vak : Wiskunde leerweg : TL toetsnummer : 4T-WIS-S06 toetsduur: : 100 minuten aantal te behalen punten : 56 punten cesuur : 28 punten toetsvorm : Schriftelijk hulpmiddelen : Geodriehoek,
Vestiging Westplasmavo vak : Wiskunde leerweg : TL toetsnummer : 4T-WIS-S06 toetsduur: : 100 minuten aantal te behalen punten : 56 punten cesuur : 28 punten toetsvorm : Schriftelijk hulpmiddelen : Geodriehoek,
Extra oefeningen hoofdstuk 12: Omtrek - Oppervlakte - Inhoud
 Extra oefeningen hoofdstuk 12: Omtrek - Oppervlakte - Inhoud 1 Een optische illusie? Welk gebied heeft de grootste oppervlakte: het gele of het donkergroene? Doe eerst een schatting en maak daarna de nodige
Extra oefeningen hoofdstuk 12: Omtrek - Oppervlakte - Inhoud 1 Een optische illusie? Welk gebied heeft de grootste oppervlakte: het gele of het donkergroene? Doe eerst een schatting en maak daarna de nodige
Computerrekenpakket Maple zesde jaar
 Computerrekenpakket Maple zesde jaar M CREATIVE COMMONS Naamsvermelding-NietCommercieel-GelijkDelen 3.0 (CC BY-NC-SA) Dit is de vereenvoudigde (human-readable) versie van de volledige licentie. De volledige
Computerrekenpakket Maple zesde jaar M CREATIVE COMMONS Naamsvermelding-NietCommercieel-GelijkDelen 3.0 (CC BY-NC-SA) Dit is de vereenvoudigde (human-readable) versie van de volledige licentie. De volledige
De tekst staat nu aan de linkerkant. De tekst staat nu aan de rechterkant. De tekst staat nu in het midden.
 1. Uitlijnen Uitlijnen: De manier waarop een regel wordt getoond. Dit kan op vier verschillende manieren. We geven hieronder vier voorbeelden. A. Links uitlijnen De tekst staat nu aan de linkerkant. B.
1. Uitlijnen Uitlijnen: De manier waarop een regel wordt getoond. Dit kan op vier verschillende manieren. We geven hieronder vier voorbeelden. A. Links uitlijnen De tekst staat nu aan de linkerkant. B.
Afsluitende Opdrachten
 Afsluitende Opdrachten A Scheve lijnen We weten hoe we het perspectiefbeeld op het tafereel moeten tekenen van een horizontale lijn. Hoe zit dat als de lijn niet horizontaal is? Daarover gaat deze opdracht.
Afsluitende Opdrachten A Scheve lijnen We weten hoe we het perspectiefbeeld op het tafereel moeten tekenen van een horizontale lijn. Hoe zit dat als de lijn niet horizontaal is? Daarover gaat deze opdracht.
Examen VWO. wiskunde B1,2. tijdvak 1 dinsdag 2 juni uur. Bij dit examen hoort een uitwerkbijlage.
 amen VWO 2009 tijdvak dinsdag 2 juni 3.30-6.30 uur wiskunde B,2 Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 9 vragen. Voor dit eamen zijn maimaal 80 punten te behalen. Voor elk vraagnummer
amen VWO 2009 tijdvak dinsdag 2 juni 3.30-6.30 uur wiskunde B,2 Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 9 vragen. Voor dit eamen zijn maimaal 80 punten te behalen. Voor elk vraagnummer
Opgave 1 Bestudeer de Uitleg, pagina 1. Laat zien dat ook voor punten buiten lijnstuk AB maar wel op lijn AB geldt: x + 3y = 5
 2 Vergelijkingen Verkennen Meetkunde Vergelijkingen Inleiding Verkennen Beantwoord de vragen bij Verkennen. Uitleg Meetkunde Vergelijkingen Uitleg Opgave Bestudeer de Uitleg, pagina. Laat zien dat ook
2 Vergelijkingen Verkennen Meetkunde Vergelijkingen Inleiding Verkennen Beantwoord de vragen bij Verkennen. Uitleg Meetkunde Vergelijkingen Uitleg Opgave Bestudeer de Uitleg, pagina. Laat zien dat ook
8.1 Rekenen met complexe getallen [1]
![8.1 Rekenen met complexe getallen [1] 8.1 Rekenen met complexe getallen [1]](/thumbs/57/40136599.jpg) 8.1 Rekenen met complexe getallen [1] Natuurlijke getallen: Dit zijn alle positieve gehele getallen en nul. 0, 1, 2, 3, 4, 5, 6,... Het symbool voor de natuurlijke getallen is Gehele getallen: Dit zijn
8.1 Rekenen met complexe getallen [1] Natuurlijke getallen: Dit zijn alle positieve gehele getallen en nul. 0, 1, 2, 3, 4, 5, 6,... Het symbool voor de natuurlijke getallen is Gehele getallen: Dit zijn
Eindexamen wiskunde B havo II
 Tonregel van Kepler In het verleden gebruikte men vaak een ton voor het opslaan en vervoeren van goederen. Tonnen worden ook nu nog gebruikt voor bijvoorbeeld de opslag van wijn. Zie de foto. foto Voor
Tonregel van Kepler In het verleden gebruikte men vaak een ton voor het opslaan en vervoeren van goederen. Tonnen worden ook nu nog gebruikt voor bijvoorbeeld de opslag van wijn. Zie de foto. foto Voor
Oefentoets Versie A. Vak: Wiskunde Onderwerp: Meetkunde Leerjaar: 1 (2017/2018) Periode: 3
 Oefentoets Versie A Vak: Wiskunde Onderwerp: Meetkunde Leerjaar: 1 (017/018) Periode: 3 Opmerkingen vooraf: Het gebruik van een rekenmachine en een tabellenboekje is toegestaan. Geef je antwoord alljd
Oefentoets Versie A Vak: Wiskunde Onderwerp: Meetkunde Leerjaar: 1 (017/018) Periode: 3 Opmerkingen vooraf: Het gebruik van een rekenmachine en een tabellenboekje is toegestaan. Geef je antwoord alljd
F3 Formules: Formule rechte lijn opstellen 1/3
 F3 Formules: Formule rechte lijn opstellen 1/3 Inleiding Bij Module F1 heb je geleerd dat Formule, Verhaal, Tabel, Grafiek en Vergelijking altijd bij elkaar horen. Bij Module F2 heb je geleerd wat een
F3 Formules: Formule rechte lijn opstellen 1/3 Inleiding Bij Module F1 heb je geleerd dat Formule, Verhaal, Tabel, Grafiek en Vergelijking altijd bij elkaar horen. Bij Module F2 heb je geleerd wat een
Uitwerkingen oefeningen hoofdstuk 4
 Uitwerkingen oefeningen hoofdstuk 4 4.4.1 Basis Lijnen en hoeken 1 Het assenstelsel met genoemde lijnen ziet er als volgt uit: 4 3 2 1 l k -4-3 -2-1 0 1 2 3 4-1 -2-3 n m -4 - Hieruit volgt: a Lijn k en
Uitwerkingen oefeningen hoofdstuk 4 4.4.1 Basis Lijnen en hoeken 1 Het assenstelsel met genoemde lijnen ziet er als volgt uit: 4 3 2 1 l k -4-3 -2-1 0 1 2 3 4-1 -2-3 n m -4 - Hieruit volgt: a Lijn k en
