Minima en maxima van functies
|
|
|
- David Brabander
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Les 3 Minima en maxima van functies Een reden waarom we de afgeleide van een functie bekijken is dat we iets over het stijgen of dalen van de functie willen weten. Als we met een differentieerbare functie te maken hebben, is de functie stijgend als de afgeleide positief is en dalend als de afgeleide negatief is. Maar soms zijn we ook geïnteresseerd in de verandering van het stijgen en dalen van een functie. Bijvoorbeeld gaat het er in de economie vaak niet om of een bedrijf een groei in de omzet heeft, maar alleen maar of de groei groter is dan de afgelopen jaren. De groei wordt beschreven door de afgeleide van de omzet-functie, de verandering van de groei door de afgeleide van de groei-functie, dus door de tweede afgeleide van de omzet-functie. We kijken dus voor een functie f(x) niet alleen maar naar de eerste afgeleide f (x) maar ook naar de tweede afgeleide f (x) := (f (x)) en ook naar hogere afgeleiden f (x) enz. Omdat het onhandig wordt, meer en meer streepjes te schrijven, gebruiken we een nieuwe notatie: We schrijven f (3) (x) voor f (x) en in het algemeen f (n) (x) voor de n-de afgeleide. Merk op: Hogere afgeleiden hoeven niet altijd te bestaan, zelfs als de functie f(x) differentieerbaar is. Bijvoorbeeld heeft de functie { x 2 als x < 0 f(x) := x 2 als x 0 de afgeleide f (x) = 2 x en is dus een differentieerbare functie, maar de tweede afgeleide bestaat voor x = 0 niet. Men zegt soms dat een functie bijvoorbeeld drievoudig differentieerbaar is, om aan te duiden dat de derde afgeleide f (x) bestaat. De beste functies (d.w.z. de meest gladde functies) zijn functies die willekeurig vaak differentieerbaar zijn. Hierbij is het toegestaan dat de n-de afgeleiden f (n) (x) vanaf een zekere n alle gelijk aan de constante 0-functie zijn. Dit is bijvoorbeeld bij veeltermfuncties van graad n het geval. Een belangrrijke toepassing van de hogere afgeleiden is de karakterisering van minima en maxima van functies. Dit zullen we in deze les uitvoerig bekijken. 3. Minima en maxima van gewone functies In veel toepassingen komt een probleem er op neer een waarde x te bepalen zo dat een functie f(x) een minimale (of maximale) waarde aanneemt. Bijvoorbeeld wordt er in de productie van blikken naar gekeken, een zo klein mogelijke hoeveelheid materiaal voor een gegeven volume te gebruiken. In de economie hangt de vraag naar een object natuurlijk ook van de prijs af. Die wordt dus zo gekozen dat het product van de prijs en het (verwachte) aantal verkochte objecten maximaal wordt. De definitie van (absolute) minima en maxima van een functie in zijn domein is heel voor de hand liggend: 30
2 A.5 Definitie Een functie f : D R heeft in a een absoluut minimum als f(a) f(x) voor alle x D. Analoog heeft een functie een absoluut maximum als f(a) f(x) voor alle x D. Soms is het ook interessant om naar lokale minima en maxima te kijken. Dat zijn punten a D zo dat f voor een klein interval om a heen een absoluut minimum/maximum in a heeft. Preciezer zeggen we: A.6 Definitie Een functie f heeft in a D een lokaal (of relatief) minimum als er een δ > 0 bestaat zo dat f(a) f(x) voor alle x (a δ, a + δ). Een functie heeft een lokaal maximum als er een δ > 0 bestaat zo dat f(a) f(x) voor alle x (a δ, a + δ). Voor willekeurige functies f kunnen we niet veel verder dan deze definities, maar als f een differentieerbare functie is, zegt de afgeleide inderdaad iets over minima en maxima. Stel dat f in a een lokaal minimum heeft en differentieerbaar in a is. Dan geldt voor kleine h < 0 dat f(a + h) f(a) en dus is f(a+h) f(a) h 0. Maar ook voor kleine h > 0 is f(a + h) f(a) en dus f(a+h) f(a) h 0. Omdat de afgeleide f f(a+h) f(a) (a) alleen maar bestaat als de limiet lim h 0 h voor h < 0 en h > 0 bestaat en dezelfde waarde heeft, is noodzakelijk f (a) = 0. Dezelfde redenering geeft ook voor een lokaal maximum dat f (a) = 0 is. We hebben dus gezien: A.7 Stelling Voor een functie f : D R, die in a D differentieerbaar is en een lokaal minimum/maximum in a heeft, geldt f (a) = 0. Helaas geldt de omkering van deze stelling niet: Bijvoorbeeld is voor f(x) = x 3 de afgeleide f (x) = 3x 2 en dus is f (0) = 0, maar 0 is geen lokaal minimum of maximum, omdat f(x) < 0 voor x < 0 en f(x) > 0 voor x > 0. Maar tenminste kunnen we met behulp van deze stelling vaak een lijstje van kandidaten x maken, waar een functie mogelijk een minimum/maximum heeft, namelijk de punten x waarvoor f (x) = 0 is en we noemen zo n punt een kritiek punt. Andere kandidaten waar een functie een lokaal minimum/maximum kan hebben maar waar we dat niet met behulp van de afgeleide kunnen zien, zijn punten waar f(x) niet differentieerbaar is. Bijvoorbeeld is f(x) = x in x = 0 niet differentieerbaar, maar zijn (absoluut) minimum zit in x = 0. Ook punten die op randpunten van het domein D liggen, moeten we apart onderzoeken. Hierbij noemen we een punt een randpunt als in een klein interval links of rechts van a geen verdere punten van D liggen, dus als [a δ, a) D = of (a, a + δ] D =. A.8 Definitie Voor een functie f(x) : D R noemen we a D een kritiek punt van f(x) als: (i) f(x) in a differentieerbaar en f (a) = 0; (ii) f(x) in a niet differentieerbaar is; 3
3 (iii) a een randpunt van D is. De kritieke punten zijn de kandidaten voor lokale minima of maxima van f(x). Hoe kunnen we nu aflezen of een functie in een punt echt een lokaal minimum of maximum heeft? Voor een lokaal minimum weten we al dat f (a) = 0 moet zijn. Verder weten we dat f(x) dalend is als f (x) 0 en stijgend als f (x) 0. Als we dus zien dat f (x) 0 voor x < a en f (x) 0 voor x > a, heeft f(x) inderdaad in a een lokaal minimum. Omgekeerd heeft f(x) een lokaal maximum in a als f (a) = 0, f (x) 0 voor x < a en f (x) 0 voor x > a. Kort gezegd heeft een functie f(x) een lokaal minimum of maximum in het punt a als het teken van de afgeleide f (x) in a verandert. Merk op dat we de ongelijkheden f (x) 0 en f (x) 0 slechts in een klein interval rond a hoeven te bekijken. Om een lokaal minimum te identificeren, kunnen we soms ook de tweede afgeleide gebruiken: Als f (a) = 0 en f (x) > 0 voor x (a δ, a + δ), dan is f (x) een op dit interval strikt stijgende functie en dus is f (x) < 0 voor x < a en f (x) > 0 voor x > a. Net zo vinden we een lokaal maximum door f (a) = 0 en f (x) < 0 op (a δ, a + δ). Dit houden we in de volgende stelling vast: A.9 Stelling Een differentieerbare functie f(x) heeft een lokaal minimum in a als er een δ > 0 bestaat zo dat f (a) = 0, f (x) 0 voor x (a δ, a) en f (x) 0 voor x (a, a + δ). Dit geldt in het bijzonder als f (a) = 0 en f (x) > 0 voor x (a δ, a + δ). Een differentieerbare functie f(x) heeft een lokaal maximum in a als er een δ > 0 bestaat zo dat f (a) = 0, f (x) 0 voor x (a δ, a) en f (x) 0 voor x (a, a + δ). Dit geldt in het bijzonder als f (a) = 0 en f (x) < 0 voor x (a δ, a + δ). Voorbeeld We gaan na hoe we de hoogte van een (gesloten) blik moeten kiezen zo dat het gebruikte materiaal (de oppervlakte) minimaal wordt. Een blik nemen we aan als een cilinder van hoogte h met als grondvlak een cirkel van straal r. Dan is het volume V van de cilinder gegeven door V = πr 2 h en de oppervlakte O door O = 2πr 2 + 2πrh = 2πr(r + h). Bij een gegeven volume willen we nu de minimale oppervlakte vinden. Uit de vergelijking voor het volume vinden we h = V π r 2, dus kunnen we O schrijven als een functie van r door O(r) = 2πr(r + V π r 2 ) = 2πr 2 + 2V r. Voor de afgeleide van O(r) geldt O (r) = 4πr 2V r 2 en we hebben O (r) = 0 4πr = 2V r 2 2πr 3 = V = πr 2 h. 32
4 r Figuur A.20: Oppervlakte van een blik van 850ml afhankelijk van de straal van het grondvlak Het geval r = 0 kunnen we rustig negeren (dan is het volume V = 0), dus volgt dat 2r = h en dus is de straal van de cirkel half zo groot als de hoogte van de blik.voor een blik met een typisch volume van 850ml vinden we dus r = 3 V 2π 5.3cm en h 0.27cm. Dit zijn inderdaad ongeveer de afmetingen van een standaardblik van dit volume. Voorbeeld 2 De kosten van een auto zijn bepaald door de kosten van de benzine en de vaste kosten die alleen maar afhankelijk zijn van de tijd die de auto rijdt. Neem aan dat de kosten voor de benzine met het kwadraat van de snelheid stijgen. Wat is dan de optimale snelheid om een gegeven afstand zo goedkoop mogelijk af te leggen? Als in de tijd t de afstand s met snelheid v gereden wordt, dan geldt v = s t. De kosten voor de benzine op een afstand s zijn dus k b = cv 2 t = cv 2 s v = csv (waarbij c de benzineprijs aangeeft) en de vaste kosten voor dezelfde afstand zijn k v = dt = d s v (voor een constante d). De totale kosten afhankelijk van de snelheid v zijn dus k(v) = csv + dsv en de afgeleide hiervan is k (v) = cs dsv 2. We hebben k (v) = 0 voor v 2 = d c, dus is de meest economische snelheid v = d c. Dit kunnen we ook kwalitatief bevestigen, want als de vaste kosten relatief hoger worden, is het goedkoper om sneller te rijden. 33
5 Voorbeeld 3 We hebben n punten a,..., a n op de x-as gegeven en willen een punt x bepalen zo dat de som f(x) := (x a ) (x a n ) 2 van de kwadratische afstanden van x van de gegeven punten minimaal wordt. Voor de afgeleide f (x) geldt f (x) = 2(x a ) (x a n ) = 2nx 2(a +... a n ). We hebben dus f (x) = 0 als x = n (a +..., a n ), dus als x het rekenkundig gemiddelde van de a i is. 3.2 Functies van meerdere variabelen en de partiële afgeleide Tot nu toe hebben we alleen maar naar functies gekeken die van één variabel afhangen. Maar in de praktijk komen we vaak functies tegen die van een aantal parameters afhangen. Bijvoorbeeld is de afstand van de oorsprong van een punt (x, y, z) in de 3-dimensionale ruimte gegeven door de functie f(x, y, z) = x 2 + y 2 + z 2 die drie variabelen heeft. Het is nu niet meer onmiddellijk duidelijk, hoe we een afgeleide van zo n functie moeten definiëren. Het zou handig zijn als de afgeleide weer de richtingscoëfficient van de raaklijn aan de grafiek van de functie is, maar het probleem is dat er in één punt raaklijnen voor elke mogelijke richting zijn. We moeten dus ook de richting aangeven in die we de raaklijn aan de grafiek willen leggen. Het belangrijkste zijn de afgeleiden in de richtingen van de coördinatenassen. Deze vinden we door alle variabelen tot op één na als constant op te vatten. Dan is de functie slechts nog een functie van de overgebleven variabel en die kunnen we met de gewone regels afleiden. Voor een functie van twee variabelen kunnen we dit ook grafisch interpreteren: De grafiek van zo n functie kunnen we zien als de verzameling van punten (x, y, f(x, y)) in de 3-dimensionale ruimte, net zo als we de grafiek van een gewone functie als de verzameling van punten (x, f(x)) in het 2-dimensionale vlak bekijken. Als we nu y tot een constante y 0 verklaren, dan kijken we naar de doorsnede van de grafiek (x, y, f(x, y)) met het vlak dat bepaald is door de vergelijking y = y 0, dus naar de punten (x, y 0, z) met z = f(x, y 0 ). Dit is een gewone grafiek van een functie in één variabel zo als in de plaatjes in Figuur A.2 te zien. Maar voor zo n doorsnede kunnen we natuurlijk zeggen wat de afgeleide zou zijn, namelijk de richtingscoëfficiënt van de raaklijn aan deze gewone grafiek. Deze afgeleide noemen we de partiële afgeleide naar x. Als we nu terug gaan naar de definitie van de gewone afgeleide, zien we dat de partiële afgeleide naar x in dit geval gegeven is door de limiet lim h 0 f(x + h, y) f(x, y). h Omdat we voor de partiële afgeleide naar x alleen maar naar de verandering van f(x, y) in de richting van x kijken, noemen we dit ook de richtingsafgeleide in de richting van x. 34
6 x x 0 y Figuur A.2: Functie f(x, y) en snede door deze functie voor y = 0.5 Analoog definiëren we nu de partiële afgeleide van een algemene functie f(x,..., x n ) van n variabelen. Voor de partiële afgeleide naar x i behandelen we de variabelen x,..., x i, x i+,..., x n als constanten (d.w.z. net zo als de constanten 5 of π) en interpreteren f zodanig als een functie van één variabel (namelijk x i ). Als we op de zo geïnterpreteerde functie de definitie van de gewone afgeleide toepassen krijgen we de volgende algemene derinitie voor de partiële afgeleide: A.0 Definitie Voor een functie f(x, x 2,..., x n ) van n variabelen heet f(x,..., x i + h,..., x n ) f(x,..., x n ) := lim x i h 0 h de partiële afgeleide van f naar x i, als deze limiet bestaat. Vaak wordt de partiële afgeleide x i ook kort als f xi geschreven. Natuurlijk gebruiken we nooit deze limiet-definitie om een partiële afgeleide te berekenen, maar passen de gewone regels voor functies van één variabel toe (waarbij we gewoon een paar constanten meer in de functie hebben). Voorbeeld: Zij f(x, y, z) de functie van drie variabelen, gegeven door f(x, y, z) := x log(yz), dan geldt: x = log(yz), y = x(yz) z = x y, z = x(yz) y = x z. Merk op dat we ook partiële afgeleide kunnen itereren, dus we kunnen x = log(yz) weer partieel afleiden. Als we dit bijvoorbeeld partieel naar y afleiden, schrijven we dit als y ( x ) = 2 f y x = (yz) z = y. 35
7 Omgekeerd kunnen we ook y partieel naar x afleiden, dit geeft y ) = x y = y. We zien dus dat het geen verschil maakt of we eerst partieel naar x en dan naar y afleiden, of andersom. y x = 2 f x ( Merk op: Het is helemaal niet vanzelfsprekend dat x y geldt, maar dit is inderdaad altijd (behalve in kunstmatig geconstrueerde gevallen) zo en heet de Stelling van Schwarz. We hoeven dus bij het achter elkaar uitvoeren van meerdere partiële afgeleiden niet op de volgorde te letten. Notatie: We hebben al gezien dat we een tweede partiële afgeleide y ( schrijven als y x. afgekort met 2 f x 2 x ) Als we twee keer in dezelfde richting afleiden, wordt dit := 2 f x x. In de vorige les hebben we gezien, dat sommige belangrijke functies door relaties met hun afgeleiden gekarakteriseerd kunnen worden. Zo is de exponentiële functie een oplossing van de differentiaalvergelijking f (x) = f(x) en de sinus en cosinus zijn oplossingen van de vergelijking f(x) + f (x) = 0. Dit soort vergelijkingen bestaat ook voor de partiële afgeleiden, we noemen zo n vergelijking een partiële differentiaalvergelijking. Als voorbeeld kijken we naar de vergelijking: x 2 2 f x 2 + 2xy 2 f x y + y2 2 f y 2 = 0. We laten zien dat de functie f(x, y) := xy x y We hebben x = y(x y) xy (x y) = y2 2 (x y) 2 Hieruit volgt 2 f y 2 = 2x2 (x y) 3 voldoet. x = 2y2 2 (x y), 3 en y een oplossing hiervan is: = x(x y)+xy (x y) 2 = x2 (x y) 2. x y = 2x(x y)2 x 2 2(x y) (x y) = 2xy 4 (x y) en 3 en we zien dat f(x, y) inderdaad aan de vergelijking In het algemeen is het oplossen van partiële differentiaalvergelijkingen een ingewikkeld probleem, meestal laten zich oplossingen alleen maar door numerieke benaderingsmethoden vinden. Soms spelen bij de beschrijving van problemen verschillende soorten van variabelen een rol, bijvoorbeeld ruimtelijke coördinaten en tijd of temperatuur en druk. Als voorbeeld hiervoor bekijken we de functie Hiervoor geldt: x 2 t f(x, y, t) := exp( t)(sin(x) + cos(y)). x = exp( t) cos(x), y = exp( t) sin(y), dus hebben we = exp( t) sin(x) en 2 f = exp( t) cos(y). Aan de andere kant geldt y 2 = exp( t)(sin(x) + cos(y)), dus voldoet de functie aan de vergelijking x f y 2 = t. Deze vergelijking beschrijft de uitbreiding van de hitte (de parameter t) op een gegeven oppervlak (met coördinaten x en y) en heet de hittevergelijking. 36
8 3.3 Minima en maxima van functies van meerdere variabelen Ook bij functies van meerdere variabelen kunnen we ons natuurlijk afvragen hoe we minima en maxima kunnen vinden. Door de interpretatie van de partiële afgeleide als richtingscoëfficient van de raaklijn parallel met een van de coördinatenassen zien we, dat in een lokaal minimum alle partiële afgeleiden gelijk aan 0 moeten zijn. Net als bij de functies van één variabel is dit alleen maar een noodzakelijke voorwaarde, maar geeft toch kandidaten voor minima en maxima. A. Stelling Een noodzakelijke voorwaarde dat een functie f(x, x 2,..., x n ) van n variabelen in een punt een lokaal minimum of maximum heeft, is dat in dit punt de partiële afgeleiden naar alle variabelen gelijk aan 0 zijn. Met behulp van deze stelling kunnen we bijvoorbeeld na gaan dat een kubus de (gesloten) doos met minimale oppervlakte voor gegeven volume is. Het volume van een doos met zijden x, y, z is geven als V = xyz de oppervlakte als O(x, y, z) = 2(xy +yz +zx). We kunnen de derde coördinaat z uitdrukken door z = V xy, dan wordt O = O(x, y) = 2(xy + V x + V y ). We hebben O x = 2(y V x 2 ) en O y = 2(x V y 2 ). Uit O x = O y = 0 volgt dus x 2 y = V en xy 2 = V. Als we deze twee vergelijkingen van elkaar aftrekken vinden we xy(x y) = 0 en hieruit volgt x = y, want voor x = 0 of y = 0 is V = 0. Dan geldt V = x 2 y = x 3 en dus is z = V xy = x y x Figuur A.22: Oppervlakte van een (gesloten) doos van volume afhankelijk van de lengten van de x- en y-zijden Hoe zou dit (niet onverwachte) resultaat veranderen als we naar een open doos zonder deksel kijken? We kunnen deze vraag ook zo interpreteren, dat het 37
9 materiaal voor bodem en deksel van een gesloten doos slechts half zo duur is als het materiaal voor de zijvlakken. Dan zouden we verwachten dat het goedkoper wordt, als we bodem en deksel iets groter en de zijvlakken iets kleiner maken. Het volume van een open doos is nog steeds V = xyz, maar de oppervlakte wordt nu O(x, y, z) = xy + 2yz + 2zx (als de z-as de verticale as is). Door weer z door V xy te vervangen krijgen we deze keer O(x, y) = xy + 2V x + 2V y. Voor de partiële afgeleiden geldt O x = y 2V x 2 uit O x en O y = x 2V y 2, dus krijgen we = 0 en O y = 0 de noodzakelijke voorwaarden x2 y = 2V en xy 2 = 2V. Deze vergelijkingen trekken we weer van elkaar af, dan volgt xy(x y) = 0 en dus x = y en dus x 3 = 2V. We hebben dus x = y = 3 2V en hieruit volgt z = 3 4 V. Tegenover de gesloten doos met x = y = z = 3 V zijn dus x en y een factor groter en de hoogte z is een factor 3 Coëfficiënten van een regressielijn kleiner. Een verdere toepassing voor het vinden van minima van een functie van meerdere variabelen ligt in het vinden van een regressielijn door een aantal gegeven punten. De regressielijn door de punten is bepaald door de eigenschap dat de som van de kwadraten van de verticale afstanden tussen de punten en de lijn minimaal wordt. Stel we hebben punten (x, y ),..., (x n, y n ) gegeven. Als we door deze punten de lijn y = ax + b leggen, wordt de som van de kwadratische afstanden gelijk aan f(a, b) := (ax + b y ) (ax n + b y n ) 2 = n (ax i + b y i ) 2. i= De partiële afgeleiden van f naar a en b zijn gegeven door a = 2(ax + b y )x (ax n + b y n )x n = b = 2(ax + b y ) (ax n + b y n ) = n 2(ax i + b y i )x i ; i= n 2(ax i + b y i ). De voorwaarden a = 0 en b = 0 kunnen we nu schrijven als een stelsel lineaire vergelijkingen voor a en b. Hiervoor is het handig een notatie van Gauss te gebruiken, namelijk een som n i= z i af te korten als [z]. Hiermee worden de partiële afgeleiden a en b herschreven tot a = 2(a[x2 ] + b[x] [yx]) en b i= = 2(a[x] + nb [y]) 38
10 en na schrappen van de 2 worden de vergelijkingen a = 0 en b = 0: a[x 2 ] + b[x] = [xy] en a[x] + nb = [y]. Uit de tweede vergelijking krijgen we b = ([y] a[x]) n en invullen hiervan in de eerste vergelijking geeft a[x 2 ] + ([y] a[x])[x] = [xy]. n Vermenigvuldigen met n en oplossen naar a geeft na[x 2 ] + [x][y] a[x] 2 = n[xy] a = n[xy] [x][y] n[x 2 ] [x] 2. Ten slotte moeten we dit resultaat nog in de vergelijking voor b invullen, dit geeft: b = n ([y] a[x]) = (n[xy] [x][y])[x] ([y] n n[x 2 ] [x] 2 ) = n n[x 2 ][y] [x] 2 [y] n[x][xy] + [x] 2 [y] n[x 2 ] [x] 2 b = [x2 ][y] [x][xy] n[x 2 ] [x] 2 = ( = [x2 ][y] [x][xy] n[x 2 ] [x] 2. Samengevat hebben we aangetoond dat de coëfficiënten van de regressielijn ax + b door de punten (x, y ),..., (x n, y n ) gegeven zijn door: n[xy] [x][y] a = n[x 2 ] [x] 2 = n( n i= x iy i ) ( n i= x i)( n i= y i) n( n i= x2 i ) ( n i= x i) 2 ; n i= x2 i )( n i= y i) ( n i= x i)( n i= x iy i ) n( n i= x2 i ) ( n i= x i) 2. Belangrijke begrippen in deze les hogere afgeleide lokaal (absoluut) minimum/maximum kritieke waarden functies van meerdere variabelen partiële afgeleide regressielijn 39
11 Opgaven 4. Bepaal voor de functie f : R R, x x 2 exp(x) de lokale minima en maxima. 5. Bepaal voor ieder van de volgende functies de lokale minima en maxima op het gegeven domein (let ook op de randpunten). (i) f : [ 2, 2 ] R, x 3x4 8x 3 + 6x 2, (ii) f : [ 2, ] R, x x 5 +x+, (iii) f : [, x+ 2 ] R, x x 2 +, (iv) f : [0, 5] \ {} R, x x x Vind lokale en globale minima en maxima voor de volgende functies (die op R met uitzondering van eventuele nulpunten van de noemer gedefinieerd zijn): (i) f(x) := x 3 x, (ii) f(x) := x 4 2x 2, (iii) f(x) := x2 2x + 2, x (iv) f(x) := x 3 x 2 8x +, (v) f(x) := x 5 + x +, (vi) f(x) := 2 + x 2 3, (vii) f(x) := x 4 3 ( x) 3, (viii) f(x) := x x, 7. Zij a > 0 en f : R R gegeven door f(x) := + x + + x a. Bepaal het absolute maximum van f. (Hint: Bepaal de afgeleide apart op de deelintervallen (, 0), (0, a) en (a, ). 8. Iemand wil van een punt A aan de oever van een 2km breed kanaal naar een punt B aan de andere oever van het kanaal. Het punt A rechtstreeks tegenover A aan het andere oever heeft een afstand van 3km van het punt B. Op het kanaal kan hij met een snelheid van 3km/h roeien, aan land loopt hij met een snelheid van 6km/h. Wat is de snelste weg om van A naar B te komen? A 2km 3km B A 9. Bepaal de hoogte en het volume van de grootste cilinder (qua volume) die in een kogel van straal r past. 20. Een ellips wordt beschreven door de vergelijking x2 a + y2 2 b =. De parameters a en 2 b geven de lengten van de twee halfassen van de ellips. Voor a = b = is de ellips een cirkel. We bekijken rechthoeken met zijden evenwijdig aan de x- en y-assen, die in de ellips liggen. Bepaal de afmetingen van de rechthoeken: (a) met maximale oppervlakte, (b) met maximale omvang, die in de ellips passen. 2. Een bal wordt uit een hoogte h 0 met snelheid v 0 verticaal omhoog of omlaag gegooid (als v 0 > 0 wordt hij omhoog gegooid, als v 0 < 0 omlaag). De hoogte van de bal wordt (afhankelijk van de tijd) door een functie h(t) beschreven, voor de snelheid v(t) geldt v(t) = h (t) en de acceleratie a(t) = v (t) = g is constant (we nemen de acceleratie met een minteken, omdat deze omlaag gericht is, de waarde van g is ongeveer 9.8m/s 2 ). 40
12 (i) Toon aan dat h(t) = 2 gt2 + v 0 t + h 0. (ii) Wat is de maximale hoogte die de bal bereikt? (iii) Wat is de snelheid waarmee de bal de grond raakt? 22. Baron Münchhausen wordt op zijn kogel met een hoek van α tegen de grond en een snelheid van v afgevuurd. Zijn traject wordt beschreven door (x, y) = (v cos(α)t, v sin(α)t g 2 t2 ), waarbij g de acceleratie door de aantrekking van de aarde is (dus ongeveer 9.8 m s 2 ). (i) Na welke tijd t komt de Baron weer naar de grond? (ii) Bepaal de hoek α zo dat de Baron zo ver als mogelijk op zijn kogel kan rijden. (iii) Als de Baron van een hogere punt (bijvoorbeeld zijn dakterras) wordt afgevuurd, moet de optimale hoek α dan groter of kleiner gekozen worden? 23. Bepaal voor elk van de volgende functies de partiële afgeleiden x naar y: (i) f(x, y) := x2 y + y2 x, (ii) f(x, y) := sin(2x + 3y), (iii) f(x, y) := arctan(x 2 y) + arctan(xy 2 ), (iv) f(x, y) := exp(x 2 + xy). en y naar x en 24. Een ellipsoïd is gegeven door de vergelijking x2 a + y2 2 b + z2 2 c = (voor a = b = c = r 2 geeft dit een kogel van straal r). Bepaal het maximale volume van een doos die in het ellipsoïd past. 4
(x x 1 ) + y 1. x x 1 x k x x x k 1
 Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Extrema van functies van meerdere variabelen
 Wiskunde voor kunstmatige intelligentie, 005 Les 3 Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde 1 de vraag behandeld hoe we minima en maxima van
Wiskunde voor kunstmatige intelligentie, 005 Les 3 Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde 1 de vraag behandeld hoe we minima en maxima van
(x x 1 ) + y 1. x x k+1 x k x k+1
 Les Talor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Les Talor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
3.2 Kritieke punten van functies van meerdere variabelen
 Wiskunde voor kunstmatige intelligentie, 007/008 Als in een kritiek punt x 0 ook de tweede afgeleide f (x 0 ) = 0 is, kunnen we nog steeds niet beslissen of de functie een minimum, maximum of een zadelpunt
Wiskunde voor kunstmatige intelligentie, 007/008 Als in een kritiek punt x 0 ook de tweede afgeleide f (x 0 ) = 0 is, kunnen we nog steeds niet beslissen of de functie een minimum, maximum of een zadelpunt
Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt. x 1 Domein(f) als voor alle x Domein(f) geldt:
 Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt x 0 Domein(f) als voor alle x Domein(f) geldt: f(x) f(x 0 ). Een functie f heeft een absoluut minimum f(x 1 ) in het punt x 1 Domein(f)
Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt x 0 Domein(f) als voor alle x Domein(f) geldt: f(x) f(x 0 ). Een functie f heeft een absoluut minimum f(x 1 ) in het punt x 1 Domein(f)
Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen):
 Deel I Voortgezette Analyse Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen): Robert C. Wrede, Murray Spiegel: (Schaum s Outline of Theory and Problems of) Advanced Calculus. McGraw-Hill
Deel I Voortgezette Analyse Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen): Robert C. Wrede, Murray Spiegel: (Schaum s Outline of Theory and Problems of) Advanced Calculus. McGraw-Hill
3. Bepaal de convergentie-eigenschappen (absoluut convergent, voorwaardelijk convergent, divergent) van de volgende reeksen: n=1. ( 1) n (n + 1)x 2n.
 Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Gaap, ja, nog een keer. In één variabele hebben we deze formule nu al een paar keer gezien:
 Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
5.7. Boekverslag door P woorden 11 januari keer beoordeeld. Wiskunde B
 Boekverslag door P. 1778 woorden 11 januari 2012 5.7 103 keer beoordeeld Vak Methode Wiskunde B Getal en ruimte Wiskunde Hoofdstuk 1 Formules en Grafieken 1.1 Lineaire verbanden Van de lijn y=ax+b is de
Boekverslag door P. 1778 woorden 11 januari 2012 5.7 103 keer beoordeeld Vak Methode Wiskunde B Getal en ruimte Wiskunde Hoofdstuk 1 Formules en Grafieken 1.1 Lineaire verbanden Van de lijn y=ax+b is de
TECHNISCHE UNIVERSITEIT EINDHOVEN
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit der Wiskunde en Informatica Tentamen van Calculus voor het schakelprogramma van B (XB03) op woensdag 0 april 03, 9:00-:00 uur De uitwerkingen van de opgaven
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit der Wiskunde en Informatica Tentamen van Calculus voor het schakelprogramma van B (XB03) op woensdag 0 april 03, 9:00-:00 uur De uitwerkingen van de opgaven
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
WI1708TH Analyse 3. College 2 12 februari Challenge the future
 WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
1. (a) Gegeven z = 2 2i, w = 1 i 3. Bereken z w. (b) Bepaal alle complexe getallen z die voldoen aan z 3 8i = 0.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
De parabool en de cirkel raken elkaar in de oorsprong; bepaal ook de coördinaten van de overige snijpunten A 1 en A 2.
 BURGERLIJK INGENIEUR-ARCHITECT - 5 SEPTEMBER 2002 BLZ 1/10 1. We beschouwen de cirkel met vergelijking x 2 + y 2 2ry = 0 en de parabool met vergelijking y = ax 2. Hierbij zijn r en a parameters waarvoor
BURGERLIJK INGENIEUR-ARCHITECT - 5 SEPTEMBER 2002 BLZ 1/10 1. We beschouwen de cirkel met vergelijking x 2 + y 2 2ry = 0 en de parabool met vergelijking y = ax 2. Hierbij zijn r en a parameters waarvoor
x a k of.x 1 a 1 / 2 + ::+.x n a n / 2 k 2 bol om a, straal k
 Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
ax + 2 dx con- vergent? n ln(n) ln(ln(n)), n=3 (d) y(x) = e 1 2 x2 e 1 2 t2 +t dt + 2
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NPB 8 januari 3, 8.3.3 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden. Maak uw redenering
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NPB 8 januari 3, 8.3.3 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden. Maak uw redenering
Machtsfuncties al dan niet samengesteld in de vorm van een polynoom- of veeltermfunctie
 Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen 0
Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen 0
1 Continuïteit en differentieerbaarheid.
 1 1 Continuïteit en differentieerbaarheid. In dit hoofdstuk bekijken we continuiteit en differentieerbaarheid voor functies van meerdere variabelen. Ter orientatie repeteren we eerst hoe het zat met functies
1 1 Continuïteit en differentieerbaarheid. In dit hoofdstuk bekijken we continuiteit en differentieerbaarheid voor functies van meerdere variabelen. Ter orientatie repeteren we eerst hoe het zat met functies
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 2008 Minimum-Maimumproblemen (versie 11 augustus 2008) Inleiding In heel wat vraagstukken gaan we op zoek naar het maimum of het minimum van een zekere grootheid.
Katholieke Universiteit Leuven September 2008 Minimum-Maimumproblemen (versie 11 augustus 2008) Inleiding In heel wat vraagstukken gaan we op zoek naar het maimum of het minimum van een zekere grootheid.
Verbanden en functies
 Verbanden en functies 0. voorkennis Stelsels vergelijkingen Je kunt een stelsel van twee lineaire vergelijkingen met twee variabelen oplossen. De oplossing van het stelsel is het snijpunt van twee lijnen.
Verbanden en functies 0. voorkennis Stelsels vergelijkingen Je kunt een stelsel van twee lineaire vergelijkingen met twee variabelen oplossen. De oplossing van het stelsel is het snijpunt van twee lijnen.
Centrale Commissie Voortentamen Wiskunde Uitwerkingen Voortentamen Wiskunde B 11 juni 2012
 Centrale Commissie Voortentamen Wiskunde Uitwerkingen Voortentamen Wiskunde B juni 22 Voorlopige versie 6 juni 22 Opgave a f (x) = x2 x 5, dus f (x) = 2 2 x 5x. Dit geeft f (x) = 2 2 2x3. f (x) = 2 2 2x3
Centrale Commissie Voortentamen Wiskunde Uitwerkingen Voortentamen Wiskunde B juni 22 Voorlopige versie 6 juni 22 Opgave a f (x) = x2 x 5, dus f (x) = 2 2 x 5x. Dit geeft f (x) = 2 2 2x3. f (x) = 2 2 2x3
Checklist Wiskunde B HAVO HML
 Checklist Wiskunde B HAVO 4 2014-2015 HML 1 Hoofdstuk 1 Lineaire vergelijkingen en lineaire ongelijkheden oplossen. Wanneer klapt het teken om? Haakjes en breuken wegwerken. Ontbinden in factoren: x buiten
Checklist Wiskunde B HAVO 4 2014-2015 HML 1 Hoofdstuk 1 Lineaire vergelijkingen en lineaire ongelijkheden oplossen. Wanneer klapt het teken om? Haakjes en breuken wegwerken. Ontbinden in factoren: x buiten
(g 0 en n een heel getal) Voor het rekenen met machten geldt ook - (p q) a = p a q a
 Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: functieverloop. 13 september 2017 dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: functieverloop 13 september 2017 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating) 1. Inleiding
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: functieverloop 13 september 2017 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating) 1. Inleiding
Functies van één veranderlijke
 Functies van één veranderlijke 191512600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl 1/43 Elektrotechniek, Wiskunde en Informatica EWI Maxima en minima Gegeven een functie f met domein
Functies van één veranderlijke 191512600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl 1/43 Elektrotechniek, Wiskunde en Informatica EWI Maxima en minima Gegeven een functie f met domein
Machtsfuncties al dan niet samengesteld in de vorm van een polynoom- of veeltermfunctie. 1) Met een positief exponent in de term(en) ( )
 Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen ).
Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen ).
P is nu het punt waarvan de x-coördinaat gelijk is aan die van het punt X en waarvan de y-coördinaat gelijk is aan AB (inclusief het teken).
 Inhoud 1. Sinus-functie 1 2. Cosinus-functie 3 3. Tangens-functie 5 4. Eigenschappen 4.1. Verband tussen goniometrische verhoudingen en goniometrische functies 8 4.2. Enkele eigenschappen van de sinus-functie
Inhoud 1. Sinus-functie 1 2. Cosinus-functie 3 3. Tangens-functie 5 4. Eigenschappen 4.1. Verband tussen goniometrische verhoudingen en goniometrische functies 8 4.2. Enkele eigenschappen van de sinus-functie
Complexe functies. 2.1 Benadering door veeltermen
 Wiskunde voor kunstmatige intelligentie, Les Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen ook functies
Wiskunde voor kunstmatige intelligentie, Les Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen ook functies
Samenvatting wiskunde havo 4 hoofdstuk 5,7,8 en vaardigheden 3 en 4 en havo 5 hoofdstuk 3 en 5 Hoofdstuk 5 afstanden en hoeken Voorkennis Stelling van
 Samenvatting wiskunde havo 4 hoofdstuk 5,7,8 en vaardigheden 3 en 4 en havo 5 hoofdstuk 3 en 5 Hoofdstuk 5 afstanden en hoeken Stelling van Kan alleen bij rechthoekige driehoeken pythagoras a 2 + b 2 =
Samenvatting wiskunde havo 4 hoofdstuk 5,7,8 en vaardigheden 3 en 4 en havo 5 hoofdstuk 3 en 5 Hoofdstuk 5 afstanden en hoeken Stelling van Kan alleen bij rechthoekige driehoeken pythagoras a 2 + b 2 =
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
Vectoranalyse voor TG
 college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
1.1 Differentiëren, geknipt voor jou
 1.1 Differentiëren, geknipt voor jou Je hebt leren omgaan met hellings of, wat hetzelfde is: s. We frissen de begrippen en rekenmethoden die hierbij horen nu wat op. Stel dat je met een (gewone) schaar
1.1 Differentiëren, geknipt voor jou Je hebt leren omgaan met hellings of, wat hetzelfde is: s. We frissen de begrippen en rekenmethoden die hierbij horen nu wat op. Stel dat je met een (gewone) schaar
V.2 Limieten van functies
 V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
V.4 Eigenschappen van continue functies
 V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
Samenvatting wiskunde B
 Samenvatting wiskunde B Dit is een samenvatting van het tweede deel van Getal en Ruimte VWO wiskunde B. In deze samenvatting worden hoofdstuk 5, 6 en 7 behandeld. Ik hoop dat deze samenvatting je zal helpen!
Samenvatting wiskunde B Dit is een samenvatting van het tweede deel van Getal en Ruimte VWO wiskunde B. In deze samenvatting worden hoofdstuk 5, 6 en 7 behandeld. Ik hoop dat deze samenvatting je zal helpen!
Uitgewerkte oefeningen
 Uitgewerkte oefeningen Algebra Oefening 1 Gegeven is de ongelijkheid: 4 x. Welke waarden voor x voldoen aan deze ongelijkheid? A) x B) x [ ] 4 C) x, [ ] D) x, Oplossing We werken de ongelijkheid uit: 4
Uitgewerkte oefeningen Algebra Oefening 1 Gegeven is de ongelijkheid: 4 x. Welke waarden voor x voldoen aan deze ongelijkheid? A) x B) x [ ] 4 C) x, [ ] D) x, Oplossing We werken de ongelijkheid uit: 4
More points, lines, and planes
 More points, lines, and planes Make your own pictures! 1. Lengtes en hoeken In het vorige college hebben we het inwendig product (inproduct) gedefinieerd. Aan de hand daarvan hebben we ook de norm (lengte)
More points, lines, and planes Make your own pictures! 1. Lengtes en hoeken In het vorige college hebben we het inwendig product (inproduct) gedefinieerd. Aan de hand daarvan hebben we ook de norm (lengte)
III.2 De ordening op R en ongelijkheden
 III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
IJkingstoets Wiskunde-Informatica-Fysica 29 juni Nummer vragenreeks: 1
 IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
De Afgeleide. ) = 2y. 2 = 4y = 4.(2x+1)
 De Afgeleide DE AFGELEIDE FUNCTIE VAN EEN GEGEVEN FUNCTIE y = f(x) = u is een andere functie genoteerd met y' die uit f'(x) wordt verkregen door toepassing van enkele basisformules. Zo is (u n ) =n.u n-1.u,
De Afgeleide DE AFGELEIDE FUNCTIE VAN EEN GEGEVEN FUNCTIE y = f(x) = u is een andere functie genoteerd met y' die uit f'(x) wordt verkregen door toepassing van enkele basisformules. Zo is (u n ) =n.u n-1.u,
3.1 Negatieve getallen vermenigvuldigen [1]
![3.1 Negatieve getallen vermenigvuldigen [1] 3.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/101/149931282.jpg) 3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
Per nieuwe hoofdvraag een nieuwe bladzijde gebruiken. De vragen hoeven niet in de juiste volgorde te worden opgelost.
 SBC AMDG Ma 13/12/04 klas : 5WEWI8 5GRWI8 Van Hijfte D. toegelaten : grafisch rekentoestel Examen Wiskunde deel I (90p) Per nieuwe hoofdvraag een nieuwe bladzijde gebruiken. De vragen hoeven niet in de
SBC AMDG Ma 13/12/04 klas : 5WEWI8 5GRWI8 Van Hijfte D. toegelaten : grafisch rekentoestel Examen Wiskunde deel I (90p) Per nieuwe hoofdvraag een nieuwe bladzijde gebruiken. De vragen hoeven niet in de
Zomercursus Wiskunde. Module 11 Minimum-Maximumproblemen (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 2011 Module 11 Minimum-Maimumproblemen (versie 22 augustus 2011) Inhoudsopgave 1 Theoretische achtergrond 1 2 Oefeningen 7 2.1 Basis (A- en B-programma)........................
Katholieke Universiteit Leuven September 2011 Module 11 Minimum-Maimumproblemen (versie 22 augustus 2011) Inhoudsopgave 1 Theoretische achtergrond 1 2 Oefeningen 7 2.1 Basis (A- en B-programma)........................
1.1 Lineaire vergelijkingen [1]
![1.1 Lineaire vergelijkingen [1] 1.1 Lineaire vergelijkingen [1]](/thumbs/62/47724253.jpg) 1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
 2004 Gemeenschappelijke proef Algebra - Analyse - Meetkunde - Driehoeksmeting 14 vragen - 2:30 uur Reeks 1 Notatie: tan x is de tangens van de hoek x, cot x is de cotangens van de hoek x Vraag 1 In een
2004 Gemeenschappelijke proef Algebra - Analyse - Meetkunde - Driehoeksmeting 14 vragen - 2:30 uur Reeks 1 Notatie: tan x is de tangens van de hoek x, cot x is de cotangens van de hoek x Vraag 1 In een
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: functieverloop. 22 juli 2015. dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: functieverloop 22 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: functieverloop 22 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
12. Uitwerkingen van de opgaven
 12. Uitwerkingen van de opgaven 12.1. Uitwerkingen opgaven van hoofdstuk 3 Opgave 3.1 3,87 0,152 641, 2 Bereken met behulp van Maxima: 2,13 7,29 78 0,62 45 (%i1) 3.87*0.152*641.2/(2.13*7.29*78*0.62*45);
12. Uitwerkingen van de opgaven 12.1. Uitwerkingen opgaven van hoofdstuk 3 Opgave 3.1 3,87 0,152 641, 2 Bereken met behulp van Maxima: 2,13 7,29 78 0,62 45 (%i1) 3.87*0.152*641.2/(2.13*7.29*78*0.62*45);
Topologie in R n 10.1
 Topologie in R n 10.1 Lengte x = (x 1,..., x n ) = x 2 1 + x2 2 + + x2 n Bol B(x 0, r) = {x : x x 0 < r} x 0 r p 1 p 3 p 1 p 2 S p 1 heet uitwendig punt p 2 heet inwendig punt p 3 heet randpunt p 1 p 3
Topologie in R n 10.1 Lengte x = (x 1,..., x n ) = x 2 1 + x2 2 + + x2 n Bol B(x 0, r) = {x : x x 0 < r} x 0 r p 1 p 3 p 1 p 2 S p 1 heet uitwendig punt p 2 heet inwendig punt p 3 heet randpunt p 1 p 3
Inhoud college 6 Basiswiskunde
 Inhoud college 6 Basiswiskunde 4.0 Taylorpolynomen (slot) Zie college 5: Vanaf 4.0 Voorbeeld 4 3. Inverse functies 3.2 Exponentiële en logaritmische functies 3.3 De natuurlijke logaritme en de exponentiële
Inhoud college 6 Basiswiskunde 4.0 Taylorpolynomen (slot) Zie college 5: Vanaf 4.0 Voorbeeld 4 3. Inverse functies 3.2 Exponentiële en logaritmische functies 3.3 De natuurlijke logaritme en de exponentiële
(iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1},
![(iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1}, (iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1},](/thumbs/58/42223000.jpg) Hoofdstuk II Calculus Les Differentiatie van functies Waarscijnlijk eeft iedereen wel een idee ervan wat een functie is, maar voor de duidelijkeid zal et andig zijn om de meest belangrijke begrippen na
Hoofdstuk II Calculus Les Differentiatie van functies Waarscijnlijk eeft iedereen wel een idee ervan wat een functie is, maar voor de duidelijkeid zal et andig zijn om de meest belangrijke begrippen na
3 Bijzondere functies
 3 Bijzondere functies Verkennen grafieken Bijzondere functies Inleiding Verkennen Probeer de drie vragen te beantwoorden. Uitleg grafieken Bijzondere functies Uitleg Opgave 1 Bekijk de eerste pagina van
3 Bijzondere functies Verkennen grafieken Bijzondere functies Inleiding Verkennen Probeer de drie vragen te beantwoorden. Uitleg grafieken Bijzondere functies Uitleg Opgave 1 Bekijk de eerste pagina van
Examen Wiskundige Basistechniek 15 oktober 2011
 Examen Wiskundige Basistechniek 15 oktober 2011 vraag 1: Gegeven is het complex getal ω = exp(i π 5 ). vraag 1.1: Als we in het complexe vlak het punt P met cartesiaanse coördinaten (x, y) vereenzelvigen
Examen Wiskundige Basistechniek 15 oktober 2011 vraag 1: Gegeven is het complex getal ω = exp(i π 5 ). vraag 1.1: Als we in het complexe vlak het punt P met cartesiaanse coördinaten (x, y) vereenzelvigen
== Tentamen Analyse 1 == Maandag 12 januari 2009, u
 == Tentamen Analyse == Maandag januari 009, 400-700u Schrijf op ieder vel je naam en studentnummer, de naam van de docent (S Hille of O van Gaans) en je studierichting Elk antwoord dient gemotiveerd te
== Tentamen Analyse == Maandag januari 009, 400-700u Schrijf op ieder vel je naam en studentnummer, de naam van de docent (S Hille of O van Gaans) en je studierichting Elk antwoord dient gemotiveerd te
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 24 oktober 22, 3.45 6.45 uur De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 24 oktober 22, 3.45 6.45 uur De uitwerkingen van de opgaven
Speciale functies. 2.1 Exponentiële functie en natuurlijke logaritme
 Wiskunde voor kunstmatige intelligentie, 006 Les Speciale functies We ebben in de vorige les een aantal elementaire functies bekeken en iervoor gezien oe we deze functies kunnen afleiden. In wezen waren
Wiskunde voor kunstmatige intelligentie, 006 Les Speciale functies We ebben in de vorige les een aantal elementaire functies bekeken en iervoor gezien oe we deze functies kunnen afleiden. In wezen waren
2.1 Lineaire functies [1]
![2.1 Lineaire functies [1] 2.1 Lineaire functies [1]](/thumbs/65/53276356.jpg) 2.1 Lineaire functies [1] De lijn heeft een helling (richtingscoëfficiënt) van 1; De lijn gaat in het punt (0,2) door de y-as; In het plaatje is de lijn y = x + 2 getekend. Omdat de grafiek een rechte
2.1 Lineaire functies [1] De lijn heeft een helling (richtingscoëfficiënt) van 1; De lijn gaat in het punt (0,2) door de y-as; In het plaatje is de lijn y = x + 2 getekend. Omdat de grafiek een rechte
Vergelijkingen van cirkels en lijnen
 Vergelijkingen van cirkels en lijnen Rechthoekig coördinatenstelsel! Cartesisch coördinatenstelsel! René Descartes (1596-1650) Van hem is de uitspraak: Ik denk, dus ik besta! September 12, 2009 1 Vergelijkingen
Vergelijkingen van cirkels en lijnen Rechthoekig coördinatenstelsel! Cartesisch coördinatenstelsel! René Descartes (1596-1650) Van hem is de uitspraak: Ik denk, dus ik besta! September 12, 2009 1 Vergelijkingen
1.0 Voorkennis. Voorbeeld 1: Los op: 6x + 28 = 30 10x.
 1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
Uitwerkingen Mei 2012. Eindexamen VWO Wiskunde B. Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek
 Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
Imaginary - singulariteiten
 Imaginary - singulariteiten Gommaar Maes en Tania Van Damme SLO Wiskunde - Universiteit Gent en Atheneum Mariakerke Inleiding Een regulier punt van een vlakke kromme is een punt waar de kromme vloeiend
Imaginary - singulariteiten Gommaar Maes en Tania Van Damme SLO Wiskunde - Universiteit Gent en Atheneum Mariakerke Inleiding Een regulier punt van een vlakke kromme is een punt waar de kromme vloeiend
Opgave a. We berekenen eerst een normaal v van V en een normaal w van W. v = (b a) (c a) = ((2)(1) ( 2)( 2), ( 2)( 1) ( 1)(1), ( 1)( 2) (2)( 1))
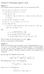 Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Opgaven voor Calculus - Oplossingen
 Wiskunde voor kunstmatie intellientie Opaven voor Calculus - Opave Bepaal de afeleiden van de volende functies: (i) f() := sin( + 2 ), (ii) f() := sin() + sin( 2 ), (iii) f() := sin(cos()), ( ) cos() (iv)
Wiskunde voor kunstmatie intellientie Opaven voor Calculus - Opave Bepaal de afeleiden van de volende functies: (i) f() := sin( + 2 ), (ii) f() := sin() + sin( 2 ), (iii) f() := sin(cos()), ( ) cos() (iv)
Vectoranalyse voor TG
 college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
Examenvragen Hogere Wiskunde I
 1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
Wiskunde 2 voor kunstmatige intelligentie (BKI 316) Bernd Souvignier
 Wiskunde voor kunstmatige intelligentie (BKI 36) Bernd Souvignier najaar 6 Inhoud I Voortgezette Analyse Les Functies van meerdere variabelen.................. 3. Continuïteit..........................
Wiskunde voor kunstmatige intelligentie (BKI 36) Bernd Souvignier najaar 6 Inhoud I Voortgezette Analyse Les Functies van meerdere variabelen.................. 3. Continuïteit..........................
Tentamen Functies en Reeksen
 Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
1 Vlaamse Wiskunde Olympiade : Eerste ronde.
 1 Vlaamse Wiskunde Olympiade 1998-1999: Eerste ronde De eerste ronde bestaat uit 30 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
1 Vlaamse Wiskunde Olympiade 1998-1999: Eerste ronde De eerste ronde bestaat uit 30 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
Relevante examenvragen , eerste examenperiode
 Relevante examenvragen 2007 2008, eerste examenperiode WAAR/VALS Zijn de volgende uitspraken waar of vals? Geef een korte argumentatie (bewijs) of een tegenvoorbeeld, eventueel aangevuld met een figuur.
Relevante examenvragen 2007 2008, eerste examenperiode WAAR/VALS Zijn de volgende uitspraken waar of vals? Geef een korte argumentatie (bewijs) of een tegenvoorbeeld, eventueel aangevuld met een figuur.
Modelvragen ijkingstoets. 1 Redeneren
 Modelvragen ijkingtoets - KU Leuven, Groep W&T - versie 26 juni 2012 1 Modelvragen ijkingstoets Onderstaande vragen staan model voor de ijkingstoets georganiseerd door de groep wetenschap en technologie
Modelvragen ijkingtoets - KU Leuven, Groep W&T - versie 26 juni 2012 1 Modelvragen ijkingstoets Onderstaande vragen staan model voor de ijkingstoets georganiseerd door de groep wetenschap en technologie
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar ste semester 10 januari 2008
 ste Bachelor Ingenieurswetenschappen Academiejaar 007-008 ste semester 0 januari 008 Analyse I. Bewijs de stelling van Bolzano-Weierstrass: elke oneindige begrensde deelverzameling van R heeft minstens
ste Bachelor Ingenieurswetenschappen Academiejaar 007-008 ste semester 0 januari 008 Analyse I. Bewijs de stelling van Bolzano-Weierstrass: elke oneindige begrensde deelverzameling van R heeft minstens
WI1708TH Analyse 3. College 5 23 februari Challenge the future
 WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
Voorbereiding toelatingsexamen arts/tandarts
 Voorbereiding toelatingsexamen artstandarts Wiskunde: oppervlakteberekening 307 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http:users.telenet.betoelating) . Inleiding Dit oefeningenoverzicht
Voorbereiding toelatingsexamen artstandarts Wiskunde: oppervlakteberekening 307 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http:users.telenet.betoelating) . Inleiding Dit oefeningenoverzicht
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 2 oktober 200, 3.45 6.45 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 2 oktober 200, 3.45 6.45 uur. De uitwerkingen van de opgaven
Primitieve functie Als f : R --> R continu is op een interval, dan noemt men F : R --> R een primiteive functie of
 Enkelvoudige integralen Kernbegrippen Onbepaalde integralen Van onbepaalde naar bepaalde integraal Bepaalde integralen Integratiemethoden Standaardintegralen Integratie door splitsing Integratie door substitutie
Enkelvoudige integralen Kernbegrippen Onbepaalde integralen Van onbepaalde naar bepaalde integraal Bepaalde integralen Integratiemethoden Standaardintegralen Integratie door splitsing Integratie door substitutie
IJkingstoets Wiskunde-Informatica-Fysica september 2018: algemene feedback
 IJkingstoets wiskunde-informatica-fysica september 8 - reeks - p. IJkingstoets Wiskunde-Informatica-Fysica september 8: algemene feedback Positionering ten opzichte van andere deelnemers In totaal namen
IJkingstoets wiskunde-informatica-fysica september 8 - reeks - p. IJkingstoets Wiskunde-Informatica-Fysica september 8: algemene feedback Positionering ten opzichte van andere deelnemers In totaal namen
d. Met de dy/dx knop vind je dat op tijdstip t =2π 6,28 het water daalt met snelheid van 0,55 m/uur. Dat is hetzelfde als 0,917 cm per minuut.
 Hoofdstuk A: Goniometrische functies. I-. a. De grafiek staat hiernaast. De periode is ongeveer,6 uur. b. De grafiek snijden met y = levert bijvoorbeeld x,00 en x,8. Het verschil is ongeveer,7 uur en dat
Hoofdstuk A: Goniometrische functies. I-. a. De grafiek staat hiernaast. De periode is ongeveer,6 uur. b. De grafiek snijden met y = levert bijvoorbeeld x,00 en x,8. Het verschil is ongeveer,7 uur en dat
INLEIDING FUNCTIES 1. COÖRDINATEN
 INLEIDING FUNCTIES 1. COÖRDINATEN...1 2. FUNCTIES...2 3. ARGUMENT EN BEELD...3 4. HET FUNCTIEVOORSCHRIFT...4 5. DE FUNCTIEWAARDETABEL...5 6. DE GRAFIEK...6 7. FUNCTIES HERKENNEN...7 8. OPLOSSINGEN...9
INLEIDING FUNCTIES 1. COÖRDINATEN...1 2. FUNCTIES...2 3. ARGUMENT EN BEELD...3 4. HET FUNCTIEVOORSCHRIFT...4 5. DE FUNCTIEWAARDETABEL...5 6. DE GRAFIEK...6 7. FUNCTIES HERKENNEN...7 8. OPLOSSINGEN...9
Uitwerkingen Mei 2012. Eindexamen HAVO Wiskunde B. Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek
 Uitwerkingen Mei 2012 Eindexamen HAVO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Vliegende parkieten Opgave 1. Het energieverbruik van de parkiet als deze vliegt met
Uitwerkingen Mei 2012 Eindexamen HAVO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Vliegende parkieten Opgave 1. Het energieverbruik van de parkiet als deze vliegt met
Eindexamen havo wiskunde B pilot 2013-I
 Beoordelingsmodel Tornadoschalen maximumscore 80 km/u komt overeen met 77,8 m/s v = 77,8 invullen in de formule geeft F, Dus de intensiteit op de Fujita-schaal is maximumscore 4 De waarde van F is dan
Beoordelingsmodel Tornadoschalen maximumscore 80 km/u komt overeen met 77,8 m/s v = 77,8 invullen in de formule geeft F, Dus de intensiteit op de Fujita-schaal is maximumscore 4 De waarde van F is dan
Lineaire afbeeldingen
 Les 2 Lineaire afbeeldingen Als een robot bij de robocup (het voetbaltoernooi voor robots een doelpunt wil maken moet hij eerst in de goede positie komen, d.w.z. geschikt achter de bal staan. Hiervoor
Les 2 Lineaire afbeeldingen Als een robot bij de robocup (het voetbaltoernooi voor robots een doelpunt wil maken moet hij eerst in de goede positie komen, d.w.z. geschikt achter de bal staan. Hiervoor
Uitwerkingen huiswerk week 4
 Calculus/analyse najaar 007 Uitwerkinen huiswerk week 4 Opave 1. Bepaal de hoote en het volume van de rootste cilinder qua volume) die in een koel van straal r past. Oplossin. We noemen de hoote van de
Calculus/analyse najaar 007 Uitwerkinen huiswerk week 4 Opave 1. Bepaal de hoote en het volume van de rootste cilinder qua volume) die in een koel van straal r past. Oplossin. We noemen de hoote van de
OEFENOPGAVEN BIJ HET TENTAMEN ANALYSE 1 (COLLEGE NAJAAR 2006). (z + 2i) 4 = 16. y 4y + 5y = 0 y(0) = 1, y (0) = 2. { 1 + xc 1 voor x > 0.
 OEFENOPGAVEN BIJ HET TENTAMEN ANALYSE (COLLEGE NAJAAR 6).. Bepaal alle oplossingen van de vergelijking (z + i) 4 = 6 in het complee vlak. a. Schrijf het getal i in poolcoördinaten. b. Bereken de rechthoekige
OEFENOPGAVEN BIJ HET TENTAMEN ANALYSE (COLLEGE NAJAAR 6).. Bepaal alle oplossingen van de vergelijking (z + i) 4 = 6 in het complee vlak. a. Schrijf het getal i in poolcoördinaten. b. Bereken de rechthoekige
15.0 Voorkennis. Herhaling rekenregels voor differentiëren: (somregel) (productregel) (quotiëntregel) n( x) ( n( x))
 5.0 Voorkennis Herhaling rekenregels voor differentiëren: f ( x) a f '( x) 0 n f ( x) ax f '( x) nax n f ( x) c g( x) f '( x) c g'( x) f ( x) g( x) h( x) f '( x) g'( x) h'( x) p( x) f ( x) g( x) p'( x)
5.0 Voorkennis Herhaling rekenregels voor differentiëren: f ( x) a f '( x) 0 n f ( x) ax f '( x) nax n f ( x) c g( x) f '( x) c g'( x) f ( x) g( x) h( x) f '( x) g'( x) h'( x) p( x) f ( x) g( x) p'( x)
Uitwerkingen tentamen Wiskunde B 16 januari 2015
 CENTRALE COMMISSIE VOORTENTAMEN WISKUNDE Uitwerkingen tentamen Wiskunde B 6 januari 5 Vraag a f(x) = (x ) f (x) = (x ) = 6 (x ) Dit geeft f () = 6 = 6. y = ax + b met y =, a = 6 en x = geeft = 6 + b b
CENTRALE COMMISSIE VOORTENTAMEN WISKUNDE Uitwerkingen tentamen Wiskunde B 6 januari 5 Vraag a f(x) = (x ) f (x) = (x ) = 6 (x ) Dit geeft f () = 6 = 6. y = ax + b met y =, a = 6 en x = geeft = 6 + b b
Lineaire algebra 1 najaar Complexe getallen
 Lineaire algebra 1 najaar 2008 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 + 1 steeds
Lineaire algebra 1 najaar 2008 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 + 1 steeds
Hints en uitwerkingen huiswerk 2013 Analyse 1 H18
 Hints en uitwerkingen huiswerk 2013 Analyse 1 H18 Rocco van Vreumingen 29 augustus 2014 1 Inhoudsopgave 1 Hints 1 3 2 Hints 2 4 3 Hints 3 5 4 Hints 4 5 5 Hints 5 6 6 Hints 6 6 7 Hints 7 6 8 Antwoorden
Hints en uitwerkingen huiswerk 2013 Analyse 1 H18 Rocco van Vreumingen 29 augustus 2014 1 Inhoudsopgave 1 Hints 1 3 2 Hints 2 4 3 Hints 3 5 4 Hints 4 5 5 Hints 5 6 6 Hints 6 6 7 Hints 7 6 8 Antwoorden
wiskunde B pilot vwo 2017-II
 Twee machten van maimumscore 5 f' ( ) = ln() + ln() Uit f' ( ) = volgt dat = Dus + = ( = ) Hieruit volgt = a+ a, met a =, moet minimaal zijn De vergelijking a = moet worden opgelost Dit geeft Hieruit volgt
Twee machten van maimumscore 5 f' ( ) = ln() + ln() Uit f' ( ) = volgt dat = Dus + = ( = ) Hieruit volgt = a+ a, met a =, moet minimaal zijn De vergelijking a = moet worden opgelost Dit geeft Hieruit volgt
Antwoorden Wiskunde B Hoofdstuk 1 boek 2
 Antwoorden Wiskunde B Hoofdstuk 1 boek 2 Antwoorden door een scholier 7212 woorden 16 maart 2005 4,6 58 keer beoordeeld Vak Wiskunde B uitwerking Havo NG/NT 2 Hoofdstuk 1 De afgeleide functie 1.1 Differentiaalquotient
Antwoorden Wiskunde B Hoofdstuk 1 boek 2 Antwoorden door een scholier 7212 woorden 16 maart 2005 4,6 58 keer beoordeeld Vak Wiskunde B uitwerking Havo NG/NT 2 Hoofdstuk 1 De afgeleide functie 1.1 Differentiaalquotient
TENTAMEN ANALYSE 1. dinsdag 3 april 2007,
 TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
IJkingstoets september 2015: statistisch rapport
 IJkingstoets burgerlijk ingenieur 4 september 05 - reeks - p. IJkingstoets september 05: statistisch rapport In totaal namen studenten deel aan deze toets. Hiervan waren er 06 geslaagd. Verdeling van de
IJkingstoets burgerlijk ingenieur 4 september 05 - reeks - p. IJkingstoets september 05: statistisch rapport In totaal namen studenten deel aan deze toets. Hiervan waren er 06 geslaagd. Verdeling van de
Wiskunde Vraag 1. Vraag 2. Vraag 3. Vraag 4 21/12/2008
 Wiskunde 007- //008 Vraag Veronderstel dat de concentraties in het bloed van stof A en van stof B omgekeerd evenredig zijn en positief. Als de concentratie van stof A met p % toeneemt, dan zal de concentratie
Wiskunde 007- //008 Vraag Veronderstel dat de concentraties in het bloed van stof A en van stof B omgekeerd evenredig zijn en positief. Als de concentratie van stof A met p % toeneemt, dan zal de concentratie
Uitwerkingen bij 1_0 Voorkennis: Vergelijkingen oplossen
 Toets om inhoudsopgave (bladwijzers) wel/niet te tonen Uitwerkingen bij 1_0 Voorkennis: Vergelijkingen oplossen! " #$ % & '&() '*& ) '#! " #" ),-. % / ---.01 2 3 ---. - / %3 -.1-01 2 4 & * 5 5 & %
Toets om inhoudsopgave (bladwijzers) wel/niet te tonen Uitwerkingen bij 1_0 Voorkennis: Vergelijkingen oplossen! " #$ % & '&() '*& ) '#! " #" ),-. % / ---.01 2 3 ---. - / %3 -.1-01 2 4 & * 5 5 & %
dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π
![dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π](/thumbs/59/43623915.jpg) Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Leerplandoelstelling Delta Nova 4 hoofdstukken en paragrafen. I Meetkunde. M1 B Bewijzen dat door drie niet-collineaire punten juist één cirkel gaat.
 Het gevolgde leerplan is D/2002/0279/047. In de onderstaande tabel vind je een overzicht van de doelstellingen en waar ze in Delta Nova 4a en 4b (leerweg 5) terug te vinden zijn. B = basisdoelstelling
Het gevolgde leerplan is D/2002/0279/047. In de onderstaande tabel vind je een overzicht van de doelstellingen en waar ze in Delta Nova 4a en 4b (leerweg 5) terug te vinden zijn. B = basisdoelstelling
Eindexamen wiskunde B1-2 havo 2002-I
 Functies In figuur 1 zijn de grafieken getekend van de functies f ( x) = 2x + 12 en g(x) = x 1. figuur 1 P f g O x 4p 1 Los op: f(x) g(x). Rond de getallen in je antwoord die niet geheel zijn af op twee
Functies In figuur 1 zijn de grafieken getekend van de functies f ( x) = 2x + 12 en g(x) = x 1. figuur 1 P f g O x 4p 1 Los op: f(x) g(x). Rond de getallen in je antwoord die niet geheel zijn af op twee
(10 pnt) Bepaal alle punten waar deze functie een relatief extreem of een zadelpunt heeft. Opgave 3. Zij D het gebied gegeven door
 Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
