(x x 1 ) + y 1. x x 1 x k x x x k 1
|
|
|
- Herman Meyer
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen van deze functies aangegeven, bijvoorbeeld dat exp(x) gekarakteriseerd is door exp(x) = exp(x) en exp() = Maar hoe we de waarde van zo n functie echt kunnen berekenen, of hoe een zakrekenmachine, GRM of computer de waarden van zo n functie berekent, hebben we toen niet gezien De methode die hiervoor (met zekere variaties) wordt gebruikt, is een functie te benaderen door een veelterm Dit lijkt op het eerste gezicht te eenvoudig om efficiënt te kunnen werken, maar men kan bewijzen dat op een begrensd gebied een continue functie door veeltermen willekeurig goed benaderd kan worden Naarmate de gewenste nauwkeurigheid toeneemt zijn hiervoor echter veeltermen van hogere graad nodig Interpolatie Eén mogelijkheid om een benaderende veelterm te vinden, gebruikt de methode van interpolatie We weten dat door punten (x, y ) en (x, y ) met verschillende x-coördinaten x x een eenduidige lineaire functie vastgelegd is, met als grafiek de lijn door deze twee punten, te weten l(x) = y y x x (x x ) + y Net zo leggen punten (weer met verschillende x-waarden) in het x y- vlak eenduidig een parabool, dus een kwadratische functie vast Op een analoge manier laat zich aantonen dat door n + punten met verschillende x-waarden een eenduidige veelterm van graad n vastgelegd is De punten x i waarop de waarden gegeven zijn noemt men ook basispunten of roosterpunten De veelterm door de punten laat zich met behulp van de Lagrange interpolatie zelfs expliciet aangeven: Stelling: De eenduidige veelterm p(x) van graad n die door de n + punten (x, y ), (x, y ),, (x n, y n ) met verschillende x-coördinaten x i loopt, is gegeven door p(x) := y L (x) + y L (x) + + y n L n (x), waarbij L k (x) := x x x k x x x x k x x x k x k x k x x k+ x k x k+ x x n x k x n De grap bij deze stelling ligt in het feit dat de hulpfuncties L k (x) juist zo gemaakt zijn dat L k (x k ) = en L k (x i ) = voor i k In Figuur I5 zien we dat de sinus functie goed door een derdegraads interpolatie p(x) benaderd wordt, die door de vier basispunten,, en loopt en 5
2 gegeven is door: p(x) = sin() x(x )(x ) sin() = ( sin() sin() + ( sin() sin() + sin() ) x + ( 5 sin() 6 + sin() ) x 4 x 556 x + 75 x x(x )(x ) + sin() x(x )(x ) 6 + sin() sin() ) x x 5 Figuur I5: Benadering van sin(x) met behulp van de Lagrange interpolatie door de punten met x-waarden,, en De interpolatie laat zich op een enigszins voor de hand liggende manier ook op functies van meerdere variabelen veralgemenen Dit heeft in het bijzonder voor punten in de -dimensionale ruimte veel toepassingen Zo worden bijvoorbeeld voor oppervlakken (zo als gezichten) alleen maar een aantal roosterpunten opgeslagen en de punten ertussen door interpolatie berekend om een glad oppervlak te krijgen Op deze manier laat zich de beweging van een computer animated figuur in de virtual reality reconstrueren uit gemeten bewegingen van een echte figuur, waarbij alleen maar op enkele punten sensoren zitten Er zijn echter ook een paar problemen als we de interpolatie willen gebruiken om een functie te benaderen: 6
3 (i) Omdat we een functie f(x) door een veelterm willen benaderen, moeten we de y k in principe al als functiewaarden y k = f(x k ) kennen, terwijl we eigenlijk de veelterm juist bepalen om de functiewaarden te kunnen benaderen (ii) Afhankelijk van hoe we de x k kiezen, kan de veelterm p(x) sterk van de functie f(x) afwijkingen, bijvoorbeeld als de x k te grote afstanden van elkaar hebben Het laatste punt is in Figuur I6 geïllustreerd: We benaderen de functie f(x) := + x op het interval [, ] door interpolaties van graad en van graad 5 In het linkerplaatje is de interpolatie met de vier basispunten,,, te zien, in het rechterplaatje de interpolatie met de zes basispunten,,,,, In beide gevallen wijkt f(x) sterk van de interpolatie af, alleen maar op het interval [, 5] is de benadering enigszins redelijk x x Figuur I6: Interpolatie van +x met 4 en 6 basispunten In principe zouden we op intervallen waar de functie f(x) heel sterk verandert veel basispunten x k willen hebben, terwijl op stukken waar de functie bijna lineair is niet zo veel basispunten nodig zijn Om hierover te kunnen beslissen moeten we naar de hogere afgeleiden van f(x) kijken en dit idee geeft aanleiding tot een andere manier om een benaderende veelterm te bepalen Deze gebruikt inderdaad de hogere afgeleiden van f(x), maar slechts in een enkele punt Taylor veeltermen Het idee bij de Taylor veelterm is, een functie f(x) in de omgeving van één punt x te benaderen Hiervoor wordt een veelterm geconstrueerd die in het punt x 7
4 niet alleen maar dezelfde functiewaarde als f(x) heeft, maar ook dezelfde eerste afgeleide, dezelfde tweede afgeleide, enzovoorts Definitie: De Taylor veelterm p(x) := p f,n,x (x) van graad n in het punt x is voor een in x (minstens) n keer differentieerbare functie f(x) vastgelegd door de eigenschappen: p(x ) = f(x ), p (x ) = f (x ), p (x ) = f (x ),, p (n) (x ) = f (n) (x ), de Taylor veelterm p(x) heeft in het punt x dus precies dezelfde afleidingen (tot orde n) als f(x) Men gaat na dat deze eigenschappen inderdaad een eenduidige veelterm van graad n bepalen, namelijk de veelterm met coëfficiënten p(x) = c n (x x ) n + c n (x x ) n + + c (x x ) + c c = f(x ), c = f (x ), c = f (x )!, c n = f (n) (x ) n! Dat dit inderdaad de coëfficiënten zijn, ziet men door het uitschrijven van de afgeleiden van p(x), invullen van x en vergelijken met f (n) (x ): p(x) = c n (x x ) n + + c (x x ) + c (x x ) + c (x x ) + c p(x ) = c, uit f(x ) = p(x ) = c volgt dan c = f(x ) p (x) = n c n (x x ) n + + c (x x ) + c (x x ) + c p (x ) = c, uit f (x ) = p (x ) = c volgt dan c = f (x ) p (x) = n(n ) c n (x x ) n + + c (x x ) + c p (x ) = c, uit f (x ) = p (x ) = c volgt dan c = f (x ) p (x) = n(n )(n ) c n (x x ) n + + c p (x ) = c c = f (x )! enzovoorts Het idee achter de geëiste eigenschappen is, dat het overeenstemmen van de hogere afgeleiden ervoor zorgt dat de grafiek van de Taylor veelterm zich rond het punt x steeds beter aan de grafiek van f(x) vlijt In Figuur I7 zien we het effect van Taylor veeltermen van verschillende graad Terwijl de veelterm van graad de grafiek van sin(x) alleen maar raakt (omdat sin(x) geen rechte stukken heeft), is de veelterm van graad al een redelijke benadering tussen ongeveer 5 en 5, voordat hij naar beneden wegduikt Met de veelterm van graad 5 gaat het iets langer goed, maar dan loopt deze naar boven weg Meestal wordt de Taylor veelterm niet in de boven aangegeven volgorde van de termen geschreven (dus beginnend met de hoogste), maar andersom Verder wordt het feit dat de Taylor veelterm de functie slechts in een kleine omgeving 8
5 5 5 y x Figuur I7: Benadering van sin(x) door de Taylor veeltermen van graad, en 5 in het punt x = π 4 van x goed benadert weergegeven door x in de vorm x = x + h te schrijven (waarbij men stiekem verondersteld dat h klein is) Dit geeft de volgende vorm van de Taylor veelterm: p(x + h) = f(x ) + f (x ) h + f (x ) h + + f (n) (x ) n! h n Opdracht 8 Bepaal voor f(x) := x de Taylor veelterm van graad 4 in het punt x = Over het verband tussen de benaderde functie f(x) en de Taylor veelterm p(x) valt echter nog veel meer te zeggen, in het bijzonder laat zich expliciet een afschatting voor de fout f(x + h) p(x + h) aangeven (die natuurlijk van h afhangt) We definiëren hiervoor de n-de foutterm R n (h) door f(x + h) = p(x + h) + R n (h) of R n (h) = f(x + h) p(x + h) Er zijn verschillende manieren om de foutterm R n (h) aan te geven, de drie 9
6 meest belangrijke zijn de volgende: R n (h) = (n + )! f (n+) (t) h n+ voor een t [, h] (Lagrange vorm) R n (h) = n! f (n+) (t) (h t) n h voor een t [, h] R n (h) = n! h f (n+) (t) (h t) n dt (Cauchy vorm) (integraal vorm) Het bewijs dat de foutterm op deze manieren geschreven kan worden is niet eens zo moeilijk Bijvoorbeeld berust de Lagrange vorm op de middelwaardestelling, die zegt, dat er voor een (differentieerbare) functie f(x) op een interval [a, b] een punt c [a, b] in het interval ligt waar de raaklijn aan f(x) dezelfde stijging heeft als de gemiddelde stijging f(b) f(a) b a van f(x) op het interval [a, b], dwz waar geldt dat f(b) f(a) = f (c)(b a) Dit klopt omdat de raaklijn niet overal een grotere of overal een kleinere stijging dan de gemiddelde stijging kan hebben Vooral de Lagrange vorm van de foutterm is vaak geschikt om de fout bij de benadering door de Taylor veelterm af te schatten Dit lukt in het bijzonder als zich makkelijk een grens voor de (n + )-de afgeleide van f(x) op het interval [, h] laat aangeven Bijvoorbeeld geldt voor f(x) = sin(x) dat f (n+) (t) voor alle t, omdat de afgeleiden ± sin(t) of ± cos(t) zijn en deze functies alleen maar waarden tussen en hebben Net zo goed ziet men in dat voor f(x) = exp(x) voor t [, h] (met h > ) geldt dat f (n+) (t) e h omdat de afgeleiden de exponentiële functie reproduceren en de exponentiële functie monotoon stijgend is Voorbeelden: () Voor f(x) := sin(x) en x = hebben we f(x ) = sin() =, f (x ) = cos() =, f (x ) = sin() =, f (x ) = cos() = en f (4) (x ) = sin() = De Taylor veelterm van graad 4 van sin(x) rond x = is dus p(x) = + x 6 x + = x 6 x Als we nu bijvoorbeeld de waarde van sin( π ) willen bepalen, krijgen we de benadering sin( π ) π 6 ( π ) = π π De fout kunnen we afschatten met R 4 ( π ) < 5! ( π )5 < 6 5 = 6, dus hebben we aangetoond dat 896 < sin( π ) < 9 () We kunnen het Euler getal e benaderen met behulp van de Taylor ontwikkeling van f(x) := exp(x) in x = Omdat f (n) (x) = exp(x), geldt f (n) () = voor alle n We krijgen daarom de n-de Taylor veelterm p(h) = + h + h + h! + + hn n!
7 Als benadering van e = f() krijgen we met n = 6 bijvoorbeeld p() = De fout kunnen we afschatten met (n+)! et n+ voor een t [, ], maar omdat we e juist willen berekenen, moeten we hier een grove afschatting voor e nemen, bijvoorbeeld e t e < Hieruit volgt dat R n () < 7! = 6, dus hebben we aangetoond dat 774 < e < Opdracht 9 Bepaal met behulp van een Taylor veelterm de waarde van sin() op 8 decimalen, dwz met een fout van hoogstens 8 Taylor reeksen Door de graad van de Taylor veelterm te laten groeien, krijgen we (in goedaardige gevallen) een steeds betere benadering van een functie, en meestal ook op een groter interval In Figuur I8 zien we bijvoorbeeld, dat de Taylor veelterm van graad (deze keer in het punt x = berekend) tussen π en π bijna niet van de functie sin(x) te onderscheiden is y - x Figuur I8: Benadering van sin(x) door de Taylor veelterm van graad in het punt x = Men krijgt dus het idee dat de benadering steeds beter wordt als we de graad verhogen, en het beste zou zijn, helemaal niet te stoppen maar oneindig door te gaan Dit doen we dus! Hier wordt nu duidelijk waarom het nuttig is de Taylor veelterm niet met de hoogste term f (n) (x ) n! h n te beginnen, maar met de laagste term f(x ), want
8 op deze manier kunnen we op een geschikte plek enzovoorts zeggen om aan te duiden, dat de veelterm met hogere termen door gaat Machtreeksen Als men een algemene veeltermen met opstijgende termen schrijft, krijgt men iets als p(x) = a + a x + a x + + a n x n = a i x i Als we nu niet met een term a n x n stoppen, maar ook voor een willekeurig hoge graad i steeds nog een coëfficiënt a i van x i definiëren (die weliswaar mag zijn), noemen we dit geen veelterm meer, maar een reeks, soms voor alle duidelijkheid zelfs een oneindige reeks Een reeks is dus een uitdrukking van de vorm r(x) = a + a x + a x + + a n x n + = i= a n x n Veeltermen zijn nu een speciale vorm van reeksen, een veelterm van graad n is namelijk een reeks waarbij vanaf i = n + geldt dat a i = is n= Er zijn twee verschillende manieren hoe men tegen een oneindige reeks aan kan kijken, van een meer algebraïsch standpunt of van een meer analytisch standpunt Algebraïsch kan men een reeks zien als een abstracte uitdrukking die gerepresenteerd is door de oneindige rij (a, a, a, ) van coëfficiënten Twee reeksen laten zich net zo optellen als men veeltermen optelt, namelijk door de coëfficiënten van iedere term x n bij elkaar op te tellen Desnoods laten zich twee reeksen ook met elkaar vermenigvuldigen, dit geeft het zogeheten convolutieproduct of Cauchy product waarbij men in het product van de twee reeksen weer de coëfficiënten van de termen x n bepaald Dit gebeurt in principe ook hetzelfde als bij veeltermen, omdat alleen maar de termen tot graad n in de twee reeksen een bijdrage aan de term x n in het product kunnen leveren Er geldt ( a n x n ) ( b n x n ) = c n x n met c n = n= n= n= a i b n i, bijvoorbeeld is c = a b + a b + a b + a b Analytisch zien we f(x) = n= a nx n als functie, waarbij we voor de functiewaarde in het punt x een limiet moeten bekijken, namelijk de limiet f(x) = lim n i= a i x i Deze limiet hoeft niet voor iedere x te bestaan, dus hebben we het alleen maar voor degene waarden x echt met een functie te maken, waar deze limiet inderdaad bestaat i=
9 Voorbeeld: Als we een voorbeeld van een reeks willen bekijken die geen veelterm is, schiet misschien als eerste de reeks door het hoofd waarbij alle coëfficiënten a n = zijn, dus de reeks r(x) = + x + x + = x n Deze reeks heet de meetkundige reeks en heeft de mooie eigenschap dat voor x < geldt dat x n = x n= n= Dit gaat men na, door het product ( + x + + x n )( x) uit te schrijven als ( + x + + x n )( x) = ( + x + + x n ) (x + x + + x n+ ) = x n+ Voor x < is lim n x n+ =, dus gaat ( + x + + x n )( x) en we moeten alleen nog door ( x) delen om de boven aangegeven formule te krijgen De Taylor reeks van een functie We gaan nu van de Taylor veeltermen een reeks maken door de graad van de veeltermen naar oneindig te laten gaan De reeks die we zo krijgen noemen we natuurlijk Taylor reeks Definitie: De oneindige reeks T (x) := T f,x (x) gedefinieerd door T (x) := lim n p f,n,x (x) = f(x ) + f (x )(x x ) + + f (n) (x ) (x x ) n + n! f (n) (x ) = (x x ) n n! n= heet de Taylor reeks van f(x) in het punt x Over de Taylor reeks als limiet van de Taylor veeltermen moeten we een paar belangrijke opmerkingen kwijt: () Natuurlijk geldt T (x ) = f(x ), omdat alle termen in de som voor n > wegvallen Maar het kan zijn dat de reeks T (x) voor geen enkele x x convergeert, dus een limiet heeft Voor goedaardige functies (zo als we die in de praktijk kunnen verwachten) geldt dit wel, tenminste in een (voldoende klein) interval rond x De vraag of en waar de Taylor reeks van een functie convergeert, geeft aanleiding tot belangrijke en diepe stellingen in de wiskunde, maar is in deze cursus een minder belangrijke vraagstelling, omdat we veronderstellen dat we het met voldoende gladde functies te maken hebben
10 () Zelfs als de Taylor reeks T (x) voor een zekere waarde x convergeert, hoeft de limiet niet de juiste functiewaarde f(x) te zijn Een afschrikkend voorbeeld hiervoor is de functie f(x) := e x die door f() := continu naar voortgezet wordt Deze functie is zelfs willekeurig vaak differentieerbaar, en er geldt f (n) () = voor alle n Dit betekent, dat de coëfficiënten van de Taylor reeks van f(x) in het punt x = alle zijn en dus de Taylor reeks T (x) = is Aan de andere kant is f(x) voor x, dus geeft de Taylor reeks de functie alleen maar in het nulpunt x = weer () De grootste afstand r zo dat T (x) voor alle x met x x < r naar de goede waarde f(x) convergeert, noemt men de convergentiestraal van T (x) Als we bij een functie f(x) ervan uit gaan dat de Taylor reeks T (x) in de punten waar hij convergeert ook naar de goede waarde f(x) convergeert, schrijven we gewoon f(x) in plaats van T (x) Net als bij de Taylor veeltermen is het ook hier gebruikelijk, duidelijk te maken dat x dicht bij het punt x ligt door x = x + h te schrijven Op deze manier krijgt men de volgende vorm van de Taylor reeks: f (n) (x ) f(x + h) = h n n! Voorbeelden: n= () exp(x): We bekijken de Taylor reeks in het punt x =, daar geldt exp (n) (x ) = exp() = voor alle n N De Taylor veelterm van graad n voor exp(x) in het punt is dus +! x +! x + + n! xn = en de Taylor reeks in het punt is de limiet n van deze veeltermen, dus x n T (x) = n! = + x + x + x 6 + x4 4 + n= Er laat zich aantonen dat deze Taylor reeks convergentiestraal heeft, dwz dat T (x) voor elke x R naar exp(x) convergeert Omdat de noemers met n! heel snel groeien, is de convergentie erg goed en kunnen we de exponentiële functie al met weinig termen goed benaderen () sin(x): Ook voor de sinus functie bepalen we de Taylor reeks in x = Merk op dat sin (x) = sin(x), sin (x) = sin (x) en sin (4) (x) = sin(x), hieruit 4 i= x i i!
11 volgt dat de afgeleiden (beginnend met de -de afgeleide sin() = ) van sin(x) in het punt x = periodiek,,,,,,,, enz zijn Dit betekent voor algemene n dat sin (n) () = en sin (n+) () = ( ) n De Taylor reeks van sin(x) in het punt is dus T (x) = ( ) n xn+ (n + )! = x x 6 + x5 x n= () cos(x): Analoog met de sinus geldt voor de cosinus dat cos (x) = cos(x), cos (x) = cos (x) en cos (4) (x) = cos(x), dus zijn hier de afgeleiden in het punt x = periodiek,,,,,,,, enz We hebben dus cos (n) () = ( ) n en cos (n+) () = De Taylor reeks van cos(x) in het punt is dus T (x) = n= ( ) n xn (n)! = x + x4 4 x6 7 + Net als bij de exponentiële functie is de convergentiestraal ook bij de Taylor reeks van de sinus en cosinus functies oneindig Verder is ook hier de convergentie van de Taylor reeks erg goed, zo dat we snel een goede benadering van sin(x) of cos(x) vinden (4) log(x): Omdat de logaritme voor x = niet gedefinieerd is, moeten we hier de Taylor reeks in een andere punt bepalen, en we kiezen hiervoor x = Maar omdat het uiteindelijk toch prettiger is om een reeks met termen x n en niet (x ) n te hebben, gebruiken we een klein trucje: In plaats van log(x) kijken we naar de functie f(x) := log(x + ) en bepalen hiervoor de Taylor reeks in het punt x = Er geldt f (x) = x+ = (x + ), f (x) = ( ) (x + ), f (x) = ( )( ) (x + ), f (4) (x) = ( )( )( ) (x + ) 4 en algemeen f (n) (x) = ( )( ) ( (n )) (x + ) n = ( ) n (n )! (x + ) n In het bijzonder is f (n) () = ( ) n (n )! en dus f (n) () Taylor reeks van log(x + ) in het punt is dus T (x) = ( ) n= n xn n! = ( )n n n = x x + x x4 4 + De Merk op dat deze Taylor reeks hoogstens convergentiestraal kan hebben, omdat de logaritme in niet gedefinieerd is Dit is echter ook de convergentiestraal, we kunnen met deze reeks dus alleen maar waarden in het 5
12 interval (, ) bepalen Maar dit stelt geen probleem voor het berekenen van log(x) voor, want voor x is x en dit ligt wel in het interval [, ] en we berekenen log(x) met behulp van de relatie log(x) = log( x ) Er valt wel nog op te merken, dat de convergentie van de reeks voor de logaritme veel slechter is dan die voor exp(x), sin(x) of cos(x), omdat de noemers met n en niet met n! groeien Opdracht Bepaal de Taylor reeks van f(x) := x + in het punt x = 4 Taylor reeksen voor functies van meerdere variabelen Tot nu toe hebben we in deze les erna gekeken hoe we een gewone functie van één variabel door een oneindige reeks kunnen beschrijven of door een veelterm kunnen benaderen die we door afbreken van de Taylor reeks krijgen De benadering van een functie f(x) door de Taylor veelterm van graad n wordt vaak ook kort de n-de benadering van f(x) genoemd De meest belangrijke van deze benaderingen zijn de de (ook al lijkt het flauw), de ste of lineaire en de de of kwadratische benadering We zullen nu kijken, hoe we Taylor veeltermen op functies van meerdere veranderlijken kunnen veralgemenen Het idee dat we hierbij hanteren is hetzelfde: We benaderen een functie f(x) : R n R door een veelterm p(x) in de n variabelen die in een vaste punt x dezelfde functiewaarde heeft als f(x) en ook dezelfde eerste, tweede enz partiële afgeleiden Om de notatie overzichtelijk te houden, zullen we weer vooral naar functies van twee variabelen kijken, de resultaten laten zich dan makkelijk ook voor n variabelen formuleren Om te beginnen moeten we afspreken wat een veelterm van meerdere variabelen is, en wat de graad daarvan is Een veelterm in de twee variabelen x en y is een (eindige) som van termen van de vorm c x i y j, waarbij we c de coëfficiënt van x i y j noemen Een zuiver product x i y j van machten van de variabelen noemt men ook en monoom De graad van een term c x i y j is de som i + j van de machten van de variabelen De graad van een veelterm is het maximum van de graden van de termen Een veelterm van graad heet een constante functie, een veelterm van graad een lineaire veelterm of lineaire functie en een veelterm van graad een kwadratische veelterm of kwadratische functie Voorbeeld: De algemene kwadratische veelterm van twee variabelen is van de vorm p(x, y) = a + b x + b y + c x + c xy + c y We zullen nu de algemene definitie van de begrippen veelterm en graad voor n variabelen geven Dit vergt enigszins veel indices en ingewikkelde notaties, maar met het geval van twee variabelen voor ogen zal het geen probleem zijn 6
13 Definitie: Een veelterm in de n variabelen x,, x n is een eindige som van termen van de vorm c x i x in n De graad van een term c x i x in n is de som i + + i n van de machten van de variabelen De graad van een veelterm is het maximum van de graden van de termen in de veelterm Voorbeelden: () De algemene lineaire veelterm in x = (x,, x n ) is p(x) = a + b x + + b n x n = a + () De algemene kwadratische veelterm is van de vorm Lineaire benadering p(x) = a + b i x i + i= i= j=i b i x i i= c ij x i x j Als we een functie f(x, y) door een lineaire veelterm p(x, y) willen benaderen, kunnen we eisen dat p(x, y ) = f(x, y ) voor een vast gekozen punt (x, y ) en dat de eerste partiële afgeleiden van p(x, y) overeenkomen met de eerste partiële afgeleiden van f(x, y) in het punt (x, y ) Voor het gemak nemen we nu nog aan, dat het vast gekozen punt (x, y ) het nulpunt (, ) is, we komen naar een algemeen punt terug door x door h := x x en y door h := y y te vervangen geldt Voor de algemene lineaire veelterm Hieruit volgt en om te bereiken dat p(, ) = a, p(, ) = f(, ), moet dus gelden dat p(x, y) = a + b x + b y p x = b en p x (, ) = b, p y = b p f p (, ) = (, ), x x p y (, ) = b f (, ) = (, ) y y a = f(, ), b = f (, ), x b 7 = f (, ) y
14 Voor de lineaire benadering van f(x, y) in het punt (x, y) = (, ) krijgen we dus de lineaire veelterm p(x, y) = f(, ) + f f (, ) x + (, ) y x y Omdat p(x, y) zo is gekozen dat de functiewaarde en de eerste partiële afgeleiden met f(x, y) overeenkomen, geeft p(x, y) juist het raakvlak aan de grafiek van f(x, y) in het punt (x, y ) aan Met behulp van de gradiënt kunnen we( de ) lineaire benadering ( ) nog iets eenvoudiger schrijven: Met de notaties x = en h = geldt: x y p(x + h) = f(x ) + f(x ) h Met deze notatie hebben we inderdaad de algemene vorm van de Taylor veelterm van graad gevonden: Stelling: Voor een functie f(x) : R n R van n variabelen is de Taylor veelterm van graad in het punt x gegeven door p(x + h) = f(x ) + f(x ) h = f(x ) + waarbij h i de i-de component van de vector h is, dus h = Kwadratische benadering Voor de algemene kwadratische veelterm geldt i= f x i (x ) h i p(x, y) = a + b x + b y + c x + c xy + c y p x = b + c x + c y en h h n p y = b + c x + c y Om naar de Taylor veelterm van graad te komen, moeten we ervoor zorgen dat naast de eerste partiële afgeleiden ook de tweede partiële afgeleiden van de algemene kwadratische veelterm p(x, y) = a + b x + b y + c x + c xy + c y in het punt (, ) met de tweede partiële afgeleiden van f(x, y) in dit punt overeenkomen Voor de eerste partiële afgeleiden geldt p x = b + c x + c y en 8 p y = b + c x + c y
15 en net als boven volgt uit p x a = f(, ), (, ) = f x b = f (, ), x b (, ) en p y Voor de tweede partiële van p(x, y) krijgen we: p x = c, p x y = p y x = c, f (, ) = y (, ) dat = f (, ) y p y = c en gelijk zetten met de tweede partiële afgeleiden van f(x, y) in het punt (, ) geeft: c = f x (, ), c = f x y (, ), c = f (, ) y Voor de kwadratische benadering van f(x, y) in het punt (x, y) = (, ) krijgen we dus de kwadratische veelterm p(x, y) = f(, ) + f f (, ) x + (, ) y x y + f x (, ) x + f x y (, ) xy + = f(, ) + f f (, ) x + (, ) y x y + ( f x (, ) x + f x y (, ) xy + f f (, ) y y y x (, ) yx + f (, ) y y ) Het opsplitsen van de term f x y (, ) xy in de som ( f x y (, ) xy + f y x (, ) yx) lijkt niet echt een vereenvoudiging, maar we zullen nu zien dat we hier wel iets aan hebben Net zo als we de eerste partiële afgeleiden in een vector, die we de gradiënt noemen, samengevat hebben, kunnen we de tweede partiële afgeleiden in een matrix samenvatten Voor een functie f(x, y) van twee variabelen geeft dit de -matrix ) H := H f := ( f x f x y f y x f y Deze matrix heet de Hesse matrix van f Voor een algemene functie f(x) van n variabelen is de Hesse matrix een n n-matrix met in de i-de rij de partiële afgeleiden naar de i-de variabel x i en in de j-de kolom de partiële afgeleiden naar x j, dus op positie (i, j) staat de tweede partiële afgeleide naar x i en x j Definitie: Voor een functie f(x) : R n R heet de matrix f x x f H := H f := f x f x x n f x x n 9 x n x f x n
16 met H ij = f x j x i de Hesse matrix van f(x) Omdat volgens de Stelling van Schwarz geldt dat Hesse matrix een symmetrische matrix, dwz er geldt H = H tr f x j x i = f x i x j, is de We noteren met H(x ) (of H(x, y) in het geval van twee variabelen) de Hesse matrix waarvoor de partiële afgeleiden in het punt x (of het punt (x, y)) geëvalueerd zijn ( ) x Voor een vector h = geldt dan: y h tr H(x ) h = f x (x ) x + f y x (x ) xy + f x y (x ) yx + f y (x ) y = f x (x ) x + f y x (x ) xy + f y (x ) y Met behulp van de Hesse matrix kunnen we Taylor veelterm van graad daarom als volgt herschrijven: p(x + h) = f(x ) + f(x ) h + htr H(x ) h Ook hier hebben we met deze notatie de algemene vorm van de Taylor veelterm van graad gevonden, er geldt: Stelling: Voor een functie f(x) : R n R van n variabelen is de Taylor veelterm van graad in het punt x gegeven door p(x + h) = f(x ) + f(x ) h + htr H(x ) h waarbij h i de i-de component van de vector h is Voorbeeld : We bekijken de functie in het punt (x, y ) = (, ) Er geldt f(x, y) := e x cos(y) f x = ex cos(y), en dus geldt voor de gradiënt ( e f = x ) cos(y) e x sin(y) f y = ex sin(y), en f(, ) = ( ) Voor de tweede partiële afgeleiden geldt f x = ex cos(y), f y x = ex sin(y), en dus krijgen we de Hesse matrix ( e H = x cos(y) e x ) sin(y) e x sin(y) e x cos(y) 4 f y = ex cos(y), met H(, ) = ( )
17 Omdat f(, ) =, zijn de Taylor veeltermen van graad en van f(x, y) gegeven door p (x, y) = + x en p (x, y) = + x + x y In Figuur I9 zijn de grafiek van de functie en de grafieken van de benadering door de Taylor veeltermen van graad en te zien Het is duidelijk dat de lineaire benadering het raakvlak aan de grafiek geeft en men ziet goed dat de kwadratische benadering in een omgeving van (, ) al redelijk goed is y 5 y 5 5 x 5 x Figuur I9: Benadering van e x cos(y) door Taylor veeltermen van graad en Voorbeeld : We bekijken de functie in het punt (x, y ) = (, π ) Er geldt f x = y cos(xy), en dus geldt voor de gradiënt ( ) y cos(xy) f = x cos(xy) f(x, y) := sin(xy) f y = x cos(xy), en f(, π ( ) ) = De lineaire benadering van f(x, y) is dus de constante f(, ) = Voor de tweede partiële afgeleiden geldt f x = y sin(xy), en dus krijgen we de Hesse matrix ( y H = sin(xy) cos(xy) xy sin(xy) f y x = cos(xy) xy sin(xy), f y = x sin(xy), 4 ) cos(xy) xy sin(xy) x sin(xy)
18 en dus H(, π ) = ( π 4 π π De Taylor veeltermen van graad van f(x, y) is dus gegeven door p(x, y) = + ( π 4 (x ) π (x )(y π ) (y π ) ) ) = π 8 (x ) π (x )(y π ) (y π ) ) In Figuur I zijn boven de grafiek van de functie en de (constante) lineaire benadering te zien, beneden de grafiek van de kwadratische benadering apart en de kwadratische benadering samen met de grafiek van de functie x y 5 x y x y x y Figuur I: Benadering van sin(xy) door Taylor veeltermen van graad (boven) en (beneden) in het punt (x, y ) = (, π ) Opdracht Bepaal voor f(x, y) := e x +y punt (, ) de Taylor veelterm van graad in het 4
19 Algemene vorm van de Taylor reeks Als we tot Taylor veeltermen van hogere graden dan en misschien zelfs tot Taylor reeksen voor functies van meerdere variabelen willen komen, wordt het vergelijken van de partiële afgeleiden van een veelterm met algemene coëfficiënten met de partiële afgeleiden van f(x) snel erg onhandig Maar gelukkig kunnen we de Taylor veeltermen en Taylor reeks voor functies van meerdere variabelen met een klein trucje ook afleiden uit de Taylor reeks voor een functie van één variabel Als we een functie f(x) in een kleine omgeving van een vast gekozen punt x bekijken, kunnen we dit schrijven als f(x + h) voor een (korte) vector h Hieruit maken we nu (kunstmatig) een nieuwe functie g(t) van een enkele variabel t, namelijk g(t) := f(x + t h) We krijgen de Taylor reeks van f(x) in het punt x door g(t) rond t = in een Taylor reeks te ontwikkelen en vinden f(x + h) door t = in deze Taylor reeks in te vullen, want f(x + h) = g() Op deze manier berekenen we f(x + h) door: f(x + h) = g() = g() + g () + g () + + n! g(n) () n + = n= n! g(n) () Voor de Taylor reeks van f(x) moeten we dus alleen maar de afgeleiden van g(t) in het punt t = bepalen De cruciale waarneming is nu als volgt: Merk op: De gewone afgeleide g (t) komt precies overeen met de definitie van de richtingsafgeleide van f(x) in de richting van h Voor een vector h = g (t) = j= i= i= h h n met componenten h i geldt daarom f x i (x + th) h i en dus g () = i= f x i (x ) h i Voor de tweede afgeleide g (t) moeten we weer de richtingsafgeleide in de richting van h nemen, dit geeft g f (t) = (x + th) h i h j en g f () = (x ) h i h j x j x i x j x i j= i= Op een soortgelijke manier krijgen we voor de derde afgeleide g f (t) = (x + th) h i h j h k, x k x j x i g () = k= j= i= k= j= i= f x k x j x i (x ) h i h j h k 4
20 en we kunnen in principe zo doorgaan tot hogere afgeleiden, de n-de term is dan een n-voudige som van de n-de partiële afgeleiden van f(x) Maar ook deze sommen zijn nog niet echt prettig om op te schrijven, daarom zullen we nu nog naar een veel gebruikte notatie kijken, waarmee de Taylor reeks voor meerdere variabelen bijna net zo eenvoudig wordt als de Taylor reeks voor functies van één variabel Het idee is, de partiële afgeleide als een soort bewerkingsvoorschrift te beschouwen, die we op een functie toepassen en die we een operator noemen In principe is dit niets nieuws, want ook de gewone afgeleide kunnen we zien als een operator die uit een functie f(x) een andere functie f (x) maakt Net zo interpreteren we nu de partiële afgeleide als een operator x f(x) de nieuwe functie x f = f x maakt die uit de functie Met deze operatoren kunnen we nu op een voor de hand liggende manier rekenen, voor de som van twee operatoren moeten we hiervoor aan- x + y x + geven, welke nieuwe functie de toepassing van y op een functie f(x) geeft Als verdere bewerkingen definiëren we ook de vermenigvuldiging van twee operatoren en het vermenigvuldigen van een operator met een constante: (c )f := c f x i x i ( + )f := f + f x i x j x i x j ( x i Hiermee krijgen we bijvoorbeeld ( x + y ) = x + y x + x j )f := f x i x j x y + y = x + y x + y Merk op: Dit is in principe dezelfde formule als de binomische formule (a + b) = a + ab + b en dit betekent dat we met de partiële afgeleiden als operatoren juist zo rekenen als met gewone variabelen h = Met behulp van de operatoren kunnen we het inproduct van een vector h h n met de gradiënt f herschrijven als f(x ) h = (h + + h n )f(x ) x x n waarbij het invullen van x aan de rechterkant natuurlijk na het toepassen van de operatoren gebeurt 44
21 Net zo krijgen we voor het product met de Hesse matrix h tr H(x ) h = (h + + h n ) f(x ) x x n De Taylor reeks voor een functie van n variabelen laat zich nu schrijven als: f(x + h) = n= n! (h x + + h n x n ) n f(x ) Voorbeeld: We berekenen de derdegraads term van de Taylor reeks voor een functie f(x, y) van twee variabelen Er geldt (a+b) = a +a b+ab +b, hieruit volgt (h x + h y ) = h x + h h y x + h h y x + h y dus is de derdegraads term van de Taylor reeks ( ) f! x (x ) h + f y x (x ) h h + f y x (x ) h h + f y (x ) h Belangrijke begrippen in deze les Lagrange interpolatie Taylor veelterm foutterm oneindige reeksen Taylor reeks lineaire/kwadratische benadering Hesse matrix partiële afgeleide als operator Opgaven Bepaal voor f(x) := ( + x) a met a R de Taylor veelterm van graad in x = Bepaal voor de volgende functies de Taylor veelterm van graad 5 in x = : (i) f(x) := + x = ( + x) ; (ii) f(x) := +x ; (iii) f(x) := x ; 45
22 (iv) f(x) := +x ; (v) f(x) := sin(x ); (vi) f(x) := e x 4 Zij f(x) := 8 + x = (8 + x) (i) Bepaal voor f(x) de Taylor veelterm van graad 4 in x = (ii) Vind met behulp van de Taylor veelterm in (i) een benadering voor 9 (iii) Geef met behulp van de Lagrange vorm van de foutterm een afschatting voor de mogelijke fout van de benadering in (ii) 5 Bepaal voor de volgende functies de Taylor reeksen in de aangeven punten: (i) f(x) := x in x = ; (ii) f(x) := e x in x = ; (iii) f(x) := sin(x + ) in x = ; (iv) f(x) := log(x) in x = 6 Vind de Taylor reeks voor f(x) := arctan(x) in x = (Hint: Er geldt arctan (x) = +x en dit laat zich voor x < schrijven als meetkundige reeks +x = x + x 4 x 6 + = n= ( )n x n ) 7 Bepaal voor de functie f(x, y) := x + y de Taylor veelterm van graad in het punt (, ) Gebruik de Taylor veelterm om de waarde van + 97 te benaderen en vergelijk het resultaat met de juiste waarde (volgens een rekenmachine) 8 Bepaal voor de volgende functies de Taylor veelterm van graad in het punt (x, y ) = (, ): (i) f(x, y) := +x +y ; (ii) f(x, y) := e x+y ; (iii) f(x, y) := e x y cos(xy); (iv) f(x, y) := sin(xy) + cos(xy) 9 Bepaal voor de volgende functies de Taylor veelterm van graad in de aangegeven punten (x, y ): (i) f(x, y) := +xy in (, ); (ii) f(x, y) := log( + x + y + xy) in (, ); (iii) f(x, y) := arctan(x + xy) in (, ); (iv) f(x, y) := x + xy + y in (, ); (v) f(x, y) := sin(x + y) in (, ); (vi) f(x, y) := sin(x) y in ( π, ); (vii) f(x, y) := +x +x +y 4 in (, ); (viii) f(x, y) := e (x ) cos(y) in (, ) Bepaal voor de volgende functies de Taylor veelterm van graad in de aangegeven punten (x, y ): (i) f(x, y) := +x y in (, ); (ii) f(x, y) := log(x + y ) in (, ); (iii) f(x, y) := cos(x + sin(y)) in (, ) 46
23 Les Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde de vraag behandeld hoe we minima en maxima van een functie kunnen vinden Het belangrijkste criterium was dat een differentieerbare functie in een lokaal extremum (minimum of maximum) een horizontale raaklijn heeft, de afgeleide van de functie in een extremum is dus noodzakelijk nul Punten met deze eigenschap hebben we kritieke punten genoemd, naast de speciale punten waar de functie niet differentieerbaar is en de randpunten van het interval waarop we de functie bekijken Classificatie van kritieke punten Het kan zijn dat een functie in een punt een horizontale raaklijn heeft, zonder in dit punt een extremum te hebben Dit is bijvoorbeeld het geval voor de functie f(x) = x in het punt x = Zo n punt noemt men ook een zadelpunt Het verschil tussen een zadelpunt en een echt extremum laat zich aan de hand van de tweede afgeleide f (x) beschrijven: Bij een minimum in het punt x is de functie links van x (dus voor x < x ) dalend en rechts van x stijgend, dus is de eerste afgeleide f (x) links van x negatief en rechts van x positief Dit betekent dat f (x) rond x stijgend is en dus geldt f (x ) > Net zo volgt uit f (x ) = en f (x ) <, dat de functie f(x) in het punt x een maximum heeft Met onze kennis van Taylor reeksen kunnen we dit nu ook van een andere kant bekijken We ontwikkelen f(x) rond een kritiek punt x met f (x ) = in een Taylor reeks, dit geeft: f(x + h) = f(x ) + f (x ) h + In een kleine omgeving van x (dus voor kleine waarden van h) kunnen we de hogere termen h, h 4, enz tegenover h verwaarlozen en we kunnen f(x) door de kwadratische functie g(h) := f(x ) + f (x ) h benaderen Omdat het bestaan van een lokaal extremum in x alleen maar van een kleine omgeving van x afhangt, heeft f(x) in x een maximum/minimum dan en slechts dan als g(h) in een maximum/minimum heeft Maar de vergelijking van g(h) beschrijft juist een parabool met toppunt (, f(x )) en deze parabool is naar boven geopend als f (x ) > en naar beneden geopend als f (x ) < De volgende twee gevallen zijn dus duidelijk: () Voor f (x ) > heeft g(h) in h = een minimum, dus heeft ook f(x) een minimum in x () Voor f (x ) < heeft g(h) in h = een maximum, dus heeft ook f(x) een maximum in x 47
(x x 1 ) + y 1. x x k+1 x k x k+1
 Les Talor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Les Talor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Complexe functies. 2.1 Benadering door veeltermen
 Wiskunde voor kunstmatige intelligentie, Les Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen ook functies
Wiskunde voor kunstmatige intelligentie, Les Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen ook functies
Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen):
 Deel I Voortgezette Analyse Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen): Robert C. Wrede, Murray Spiegel: (Schaum s Outline of Theory and Problems of) Advanced Calculus. McGraw-Hill
Deel I Voortgezette Analyse Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen): Robert C. Wrede, Murray Spiegel: (Schaum s Outline of Theory and Problems of) Advanced Calculus. McGraw-Hill
Extrema van functies van meerdere variabelen
 Wiskunde voor kunstmatige intelligentie, 005 Les 3 Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde 1 de vraag behandeld hoe we minima en maxima van
Wiskunde voor kunstmatige intelligentie, 005 Les 3 Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde 1 de vraag behandeld hoe we minima en maxima van
3.2 Kritieke punten van functies van meerdere variabelen
 Wiskunde voor kunstmatige intelligentie, 007/008 Als in een kritiek punt x 0 ook de tweede afgeleide f (x 0 ) = 0 is, kunnen we nog steeds niet beslissen of de functie een minimum, maximum of een zadelpunt
Wiskunde voor kunstmatige intelligentie, 007/008 Als in een kritiek punt x 0 ook de tweede afgeleide f (x 0 ) = 0 is, kunnen we nog steeds niet beslissen of de functie een minimum, maximum of een zadelpunt
Inhoud college 5 Basiswiskunde Taylorpolynomen
 Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Minima en maxima van functies
 Les 3 Minima en maxima van functies Een reden waarom we de afgeleide van een functie bekijken is dat we iets over het stijgen of dalen van de functie willen weten. Als we met een differentieerbare functie
Les 3 Minima en maxima van functies Een reden waarom we de afgeleide van een functie bekijken is dat we iets over het stijgen of dalen van de functie willen weten. Als we met een differentieerbare functie
Wiskunde 2 voor kunstmatige intelligentie (BKI 316) Bernd Souvignier
 Wiskunde voor kunstmatige intelligentie (BKI 36) Bernd Souvignier najaar 6 Inhoud I Voortgezette Analyse Les Functies van meerdere variabelen.................. 3. Continuïteit..........................
Wiskunde voor kunstmatige intelligentie (BKI 36) Bernd Souvignier najaar 6 Inhoud I Voortgezette Analyse Les Functies van meerdere variabelen.................. 3. Continuïteit..........................
Tentamen Functies en Reeksen
 Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Inhoud college 4 Basiswiskunde. 2.6 Hogere afgeleiden 2.8 Middelwaardestelling 2.9 Impliciet differentiëren 4.9 Linearisatie
 Inhoud college 4 Basiswiskunde 2.6 Hogere afgeleiden 2.8 Middelwaardestelling 2.9 Impliciet differentiëren 4.9 Linearisatie 2 Basiswiskunde_College_4.nb 2.6 Hogere afgeleiden De afgeleide f beschrijft
Inhoud college 4 Basiswiskunde 2.6 Hogere afgeleiden 2.8 Middelwaardestelling 2.9 Impliciet differentiëren 4.9 Linearisatie 2 Basiswiskunde_College_4.nb 2.6 Hogere afgeleiden De afgeleide f beschrijft
Opgaven Functies en Reeksen. E.P. van den Ban
 Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
1 Continuïteit en differentieerbaarheid.
 1 1 Continuïteit en differentieerbaarheid. In dit hoofdstuk bekijken we continuiteit en differentieerbaarheid voor functies van meerdere variabelen. Ter orientatie repeteren we eerst hoe het zat met functies
1 1 Continuïteit en differentieerbaarheid. In dit hoofdstuk bekijken we continuiteit en differentieerbaarheid voor functies van meerdere variabelen. Ter orientatie repeteren we eerst hoe het zat met functies
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.1, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 21 april, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 32 Outline 1 K. P. Hart TW2040: Complexe Functietheorie
TW2040: Complexe Functietheorie week 4.1, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 21 april, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 32 Outline 1 K. P. Hart TW2040: Complexe Functietheorie
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt. x 1 Domein(f) als voor alle x Domein(f) geldt:
 Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt x 0 Domein(f) als voor alle x Domein(f) geldt: f(x) f(x 0 ). Een functie f heeft een absoluut minimum f(x 1 ) in het punt x 1 Domein(f)
Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt x 0 Domein(f) als voor alle x Domein(f) geldt: f(x) f(x 0 ). Een functie f heeft een absoluut minimum f(x 1 ) in het punt x 1 Domein(f)
V.2 Limieten van functies
 V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
Technische Universiteit Delft Tentamen Calculus TI1106M - Uitwerkingen. 2. Geef berekeningen en beargumenteer je antwoorden.
 Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
3. Bepaal de convergentie-eigenschappen (absoluut convergent, voorwaardelijk convergent, divergent) van de volgende reeksen: n=1. ( 1) n (n + 1)x 2n.
 Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Functies van één veranderlijke
 Functies van één veranderlijke 191512600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl 1/43 Elektrotechniek, Wiskunde en Informatica EWI Maxima en minima Gegeven een functie f met domein
Functies van één veranderlijke 191512600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl 1/43 Elektrotechniek, Wiskunde en Informatica EWI Maxima en minima Gegeven een functie f met domein
Overzicht Fourier-theorie
 B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
Examenvragen Hogere Wiskunde I
 1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
ax + 2 dx con- vergent? n ln(n) ln(ln(n)), n=3 (d) y(x) = e 1 2 x2 e 1 2 t2 +t dt + 2
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NPB 8 januari 3, 8.3.3 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden. Maak uw redenering
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NPB 8 januari 3, 8.3.3 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden. Maak uw redenering
Primitieve functie Als f : R --> R continu is op een interval, dan noemt men F : R --> R een primiteive functie of
 Enkelvoudige integralen Kernbegrippen Onbepaalde integralen Van onbepaalde naar bepaalde integraal Bepaalde integralen Integratiemethoden Standaardintegralen Integratie door splitsing Integratie door substitutie
Enkelvoudige integralen Kernbegrippen Onbepaalde integralen Van onbepaalde naar bepaalde integraal Bepaalde integralen Integratiemethoden Standaardintegralen Integratie door splitsing Integratie door substitutie
Vectoranalyse voor TG
 college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
Functieonderzoek. f(x) = x2 4 x 4 + 2. Igor Voulis. 9 december 2009. 1 De functie en haar definitiegebied 2. 2 Het tekenverloop van de functie 2
 Functieonderzoek f(x) = x2 4 x 4 + 2 Igor Voulis 9 december 2009 Inhoudsopgave 1 De functie en haar definitiegebied 2 2 Het tekenverloop van de functie 2 3 De asymptoten 3 4 De eerste afgeleide 3 5 De
Functieonderzoek f(x) = x2 4 x 4 + 2 Igor Voulis 9 december 2009 Inhoudsopgave 1 De functie en haar definitiegebied 2 2 Het tekenverloop van de functie 2 3 De asymptoten 3 4 De eerste afgeleide 3 5 De
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
1. Orthogonale Hyperbolen
 . Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
. Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
TRILLINGEN EN GOLVEN HANDOUT FOURIER
 TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 2 oktober 200, 3.45 6.45 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 2 oktober 200, 3.45 6.45 uur. De uitwerkingen van de opgaven
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Lineaire algebra 1 najaar Complexe getallen
 Lineaire algebra 1 najaar 2008 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 + 1 steeds
Lineaire algebra 1 najaar 2008 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 + 1 steeds
Opgaven Inleiding Analyse
 Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van limiet dat lim y 0 y = 0. (b) Bewijs lim y 0 y 3 = 0 uit de definitie van limiet. (c)
Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van limiet dat lim y 0 y = 0. (b) Bewijs lim y 0 y 3 = 0 uit de definitie van limiet. (c)
8. Differentiaal- en integraalrekening
 Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Speciale functies. 2.1 Exponentiële functie en natuurlijke logaritme
 Wiskunde voor kunstmatige intelligentie, 006 Les Speciale functies We ebben in de vorige les een aantal elementaire functies bekeken en iervoor gezien oe we deze functies kunnen afleiden. In wezen waren
Wiskunde voor kunstmatige intelligentie, 006 Les Speciale functies We ebben in de vorige les een aantal elementaire functies bekeken en iervoor gezien oe we deze functies kunnen afleiden. In wezen waren
Inleiding Analyse. Opgaven. E.P. van den Ban. c Mathematisch Instituut Universiteit Utrecht Voorjaar 2003, herzien
 Inleiding Analyse Opgaven E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Voorjaar 2003, herzien 0 1 1 Limieten en continuïteit Opgave 1.1 (a) Bewijs direct uit de definitie van limiet dat
Inleiding Analyse Opgaven E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Voorjaar 2003, herzien 0 1 1 Limieten en continuïteit Opgave 1.1 (a) Bewijs direct uit de definitie van limiet dat
TECHNISCHE UNIVERSITEIT EINDHOVEN
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit der Wiskunde en Informatica Tentamen van Calculus voor het schakelprogramma van B (XB03) op woensdag 0 april 03, 9:00-:00 uur De uitwerkingen van de opgaven
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit der Wiskunde en Informatica Tentamen van Calculus voor het schakelprogramma van B (XB03) op woensdag 0 april 03, 9:00-:00 uur De uitwerkingen van de opgaven
V.4 Eigenschappen van continue functies
 V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde
 Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde 3 voor B. Functies van twee variabelen.. Een functie fx, y) van twee variabelen kan analoog aan een functie van één variabele in Maple
Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde 3 voor B. Functies van twee variabelen.. Een functie fx, y) van twee variabelen kan analoog aan een functie van één variabele in Maple
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op maandag 4 januari 2, 8.45.45 uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op maandag 4 januari 2, 8.45.45 uur. De uitwerkingen van de opgaven dienen
Hints en uitwerkingen huiswerk 2013 Analyse 1 H18
 Hints en uitwerkingen huiswerk 2013 Analyse 1 H18 Rocco van Vreumingen 29 augustus 2014 1 Inhoudsopgave 1 Hints 1 3 2 Hints 2 4 3 Hints 3 5 4 Hints 4 5 5 Hints 5 6 6 Hints 6 6 7 Hints 7 6 8 Antwoorden
Hints en uitwerkingen huiswerk 2013 Analyse 1 H18 Rocco van Vreumingen 29 augustus 2014 1 Inhoudsopgave 1 Hints 1 3 2 Hints 2 4 3 Hints 3 5 4 Hints 4 5 5 Hints 5 6 6 Hints 6 6 7 Hints 7 6 8 Antwoorden
dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π
![dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π](/thumbs/59/43623915.jpg) Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
12. Uitwerkingen van de opgaven
 12. Uitwerkingen van de opgaven 12.1. Uitwerkingen opgaven van hoofdstuk 3 Opgave 3.1 3,87 0,152 641, 2 Bereken met behulp van Maxima: 2,13 7,29 78 0,62 45 (%i1) 3.87*0.152*641.2/(2.13*7.29*78*0.62*45);
12. Uitwerkingen van de opgaven 12.1. Uitwerkingen opgaven van hoofdstuk 3 Opgave 3.1 3,87 0,152 641, 2 Bereken met behulp van Maxima: 2,13 7,29 78 0,62 45 (%i1) 3.87*0.152*641.2/(2.13*7.29*78*0.62*45);
Analyse I. 2. Formuleer en bewijs de formule van Taylor voor een functie f : R R. Stel de formules op voor de resttermen van Lagrange en Liouville.
 Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
1. (a) Formuleer het Cauchy criterium voor de convergentie van een reeks
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 7 augustus 2015, 16:30 19:30 (20:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 7 augustus 2015, 16:30 19:30 (20:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek
(iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1},
![(iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1}, (iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1},](/thumbs/58/42223000.jpg) Hoofdstuk II Calculus Les Differentiatie van functies Waarscijnlijk eeft iedereen wel een idee ervan wat een functie is, maar voor de duidelijkeid zal et andig zijn om de meest belangrijke begrippen na
Hoofdstuk II Calculus Les Differentiatie van functies Waarscijnlijk eeft iedereen wel een idee ervan wat een functie is, maar voor de duidelijkeid zal et andig zijn om de meest belangrijke begrippen na
Gaap, ja, nog een keer. In één variabele hebben we deze formule nu al een paar keer gezien:
 Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking Tentamen Calculus, 2DM10, maandag 22 januari 2007
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
Technische Universiteit Delft. ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW2030 Vrijdag 30 januari 2015,
 Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
1. (a) Gegeven z = 2 2i, w = 1 i 3. Bereken z w. (b) Bepaal alle complexe getallen z die voldoen aan z 3 8i = 0.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
5.1 Constructie van de complexe getallen
 Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Het oplossen van vergelijkingen Voor het benaderen van oplossingen van vergelijkingen van de vorm F(x)=0 bespreken we een aantal methoden:
 Hoofdstuk 4 Programmeren met de GR Toevoegen: een inleiding op het programmeren met de GR Hoofdstuk 5 - Numerieke methoden Numerieke wiskunde is een deelgebied van de wiskunde waarin algoritmes voor problemen
Hoofdstuk 4 Programmeren met de GR Toevoegen: een inleiding op het programmeren met de GR Hoofdstuk 5 - Numerieke methoden Numerieke wiskunde is een deelgebied van de wiskunde waarin algoritmes voor problemen
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie
 FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Analyse A, deeltentamen Uitwerkingen maandag 1 november 2010, 9 11 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Analyse A, deeltentamen Uitwerkingen maandag 1 november 2010, 9 11 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan
Wiskunde met (bedrijfs)economische toepassingen
 FACULTEIT TEW Wiskunde met (bedrijfs)economische toepassingen Oefenexamens 1ste Bachelor TEW Eerste deel (januari) Academiejaar 2013-2014 Het examen vindt voor iedereen plaats in twee delen : het eerste
FACULTEIT TEW Wiskunde met (bedrijfs)economische toepassingen Oefenexamens 1ste Bachelor TEW Eerste deel (januari) Academiejaar 2013-2014 Het examen vindt voor iedereen plaats in twee delen : het eerste
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (15126) op dinsdag 4 januari 211, 8.45 11.45 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (15126) op dinsdag 4 januari 211, 8.45 11.45 uur. De uitwerkingen van de opgaven
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
== Hertentamen Analyse 1 == Dinsdag 25 maart 2008, u
 == Hertentamen Analyse == Dinsdag 5 maart 8, 4-7u Schrijf op ieder vel je naam en studentnummer, de naam van de docent (S Hille, O van Gaans) en je studierichting Geef niet alleen antwoorden, leg elke
== Hertentamen Analyse == Dinsdag 5 maart 8, 4-7u Schrijf op ieder vel je naam en studentnummer, de naam van de docent (S Hille, O van Gaans) en je studierichting Geef niet alleen antwoorden, leg elke
Complexe getallen. 5.1 Constructie van de complexe getallen
 Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Dit is in feite de ongelijkheid van Cauchy Schwarz voor het standaardinproduct in R s van de vectoren
 Dit is in feite de ongelijkheid van Cauchy Schwarz voor het standaardinproduct in R s van de vectoren a = (a 1,..., a s ) en b = (b 1,..., b s ). Toepassing van deze Cauchy Schwarz-ongelijkheid levert
Dit is in feite de ongelijkheid van Cauchy Schwarz voor het standaardinproduct in R s van de vectoren a = (a 1,..., a s ) en b = (b 1,..., b s ). Toepassing van deze Cauchy Schwarz-ongelijkheid levert
Doe de noodzakelijke berekeningen met de hand; gebruik Maple ter controle.
 De n-de term van de numerieke rij (t n ) (met n = 0,, 2,...) is het rekenkundig gemiddelde van zijn twee voorgangers. (a) Bepaal het Z-beeld F van deze numerieke rij en het bijhorende convergentiegebied.
De n-de term van de numerieke rij (t n ) (met n = 0,, 2,...) is het rekenkundig gemiddelde van zijn twee voorgangers. (a) Bepaal het Z-beeld F van deze numerieke rij en het bijhorende convergentiegebied.
== Uitwerkingen Tentamen Analyse 1, WI1600 == Maandag 10 januari 2011, u
 == en Tentamen Analyse, WI6 == Maandag januari, 4.-7.u Technische Universiteit Delft, Faculteit EWI. Gegeven is de functie + e + e arctan,, f = +, >. a Beargumenteer dat f continu is op R. b Bepaal de
== en Tentamen Analyse, WI6 == Maandag januari, 4.-7.u Technische Universiteit Delft, Faculteit EWI. Gegeven is de functie + e + e arctan,, f = +, >. a Beargumenteer dat f continu is op R. b Bepaal de
(g 0 en n een heel getal) Voor het rekenen met machten geldt ook - (p q) a = p a q a
 Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
Wiskundige Technieken 1 Uitwerkingen Tentamen 3 november 2014
 Wiskundige Technieken Uitwerkingen Tentamen 3 november 0 Normering voor pt vragen andere vragen naar rato): pt 3pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met enkele onbelangrijke rekenfoutjes
Wiskundige Technieken Uitwerkingen Tentamen 3 november 0 Normering voor pt vragen andere vragen naar rato): pt 3pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met enkele onbelangrijke rekenfoutjes
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 24 oktober 22, 3.45 6.45 uur De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 24 oktober 22, 3.45 6.45 uur De uitwerkingen van de opgaven
Wiskunde 2 voor kunstmatige intelligentie (BKI 316) Bernd Souvignier
 Wiskunde 2 voor kunstmatige intelligentie (BKI 316) Bernd Souvignier najaar 2004 Deel I Voortgezette Analyse Les 1 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat
Wiskunde 2 voor kunstmatige intelligentie (BKI 316) Bernd Souvignier najaar 2004 Deel I Voortgezette Analyse Les 1 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat
Infi A oefententamen ψ
 Infi A oefententamen ψ Aanwijzingen Motiveer alle antwoorden. Werk rustig, netjes en duidelijk. Zorg dat je uitwerking maar één interpretatie toelaat. Alle informatie op dit opgavenblad mag bij alle (deel)opgaven
Infi A oefententamen ψ Aanwijzingen Motiveer alle antwoorden. Werk rustig, netjes en duidelijk. Zorg dat je uitwerking maar één interpretatie toelaat. Alle informatie op dit opgavenblad mag bij alle (deel)opgaven
WI1708TH Analyse 3. College 2 12 februari Challenge the future
 WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
Inleiding Analyse 2009
 Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Het uitwendig product van twee vectoren
 Het uitwendig product van twee vectoren Als u, v R 3, u = u 1, u 2, u 3 en v = v 1, v 2, v 3 dan is het uitwendig product van u en v gelijk aan een vector in R 3 en wel u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3,
Het uitwendig product van twee vectoren Als u, v R 3, u = u 1, u 2, u 3 en v = v 1, v 2, v 3 dan is het uitwendig product van u en v gelijk aan een vector in R 3 en wel u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3,
Inhoud college 6 Basiswiskunde
 Inhoud college 6 Basiswiskunde 4.0 Taylorpolynomen (slot) Zie college 5: Vanaf 4.0 Voorbeeld 4 3. Inverse functies 3.2 Exponentiële en logaritmische functies 3.3 De natuurlijke logaritme en de exponentiële
Inhoud college 6 Basiswiskunde 4.0 Taylorpolynomen (slot) Zie college 5: Vanaf 4.0 Voorbeeld 4 3. Inverse functies 3.2 Exponentiële en logaritmische functies 3.3 De natuurlijke logaritme en de exponentiële
Inverse functies en limieten
 Inverse functies en limieten Inverse functies We nemen aan dat A en B deelverzamelingen zijn van R. Een functie f : A B heet één-één duidig of injectief als f (x 1 ) f (x 2 ) voor alle x 1 x 2, x 1, x
Inverse functies en limieten Inverse functies We nemen aan dat A en B deelverzamelingen zijn van R. Een functie f : A B heet één-één duidig of injectief als f (x 1 ) f (x 2 ) voor alle x 1 x 2, x 1, x
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Ter Leering ende Vermaeck
 Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Opgaven Inleiding Analyse
 Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
WI1708TH Analyse 3. College 5 23 februari Challenge the future
 WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
Complexe functies. f(z) = z 3 + z 2. zien. Invullen van z = x + iy geeft
 Wiskunde voor kunstmatige intelligentie, 7/8 Les 6 Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen
Wiskunde voor kunstmatige intelligentie, 7/8 Les 6 Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen
168 HOOFDSTUK 5. REEKSONTWIKKELINGEN
 168 HOOFDSTUK 5. REEKSONTWIKKELINGEN 5.7 Vraagstukken Vraagstuk 5.7.1 Beschouw de differentiaalvergelijking d2 y d 2 = 2 y. (i) Schrijf y = a k k. Geef een recurrente betrekking voor de coëfficienten a
168 HOOFDSTUK 5. REEKSONTWIKKELINGEN 5.7 Vraagstukken Vraagstuk 5.7.1 Beschouw de differentiaalvergelijking d2 y d 2 = 2 y. (i) Schrijf y = a k k. Geef een recurrente betrekking voor de coëfficienten a
Reeksnr.: Naam: t 2. arcsin x f(t) = 2 dx. 1 x
 Calculus, 4//4. Gegeven de reële functie ft) met als voorschrift t arcsin x ft) = dx x a) Geef het domein van de functie ft). Op dit domein, bespreek waar de functie stijgt, daalt en bepaal de lokale extrema.
Calculus, 4//4. Gegeven de reële functie ft) met als voorschrift t arcsin x ft) = dx x a) Geef het domein van de functie ft). Op dit domein, bespreek waar de functie stijgt, daalt en bepaal de lokale extrema.
x a k of.x 1 a 1 / 2 + ::+.x n a n / 2 k 2 bol om a, straal k
 Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam and Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott.htm Overzicht Boek: Optimization: Insights and Applications,
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam and Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott.htm Overzicht Boek: Optimization: Insights and Applications,
III.2 De ordening op R en ongelijkheden
 III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
Wiskundige Technieken 1 Uitwerkingen Tentamen 4 november 2013
 Wiskundige Technieken Uitwerkingen Tentamen 4 november 0 Normering voor 4 pt vragen andere vragen naar rato): 4pt pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
Wiskundige Technieken Uitwerkingen Tentamen 4 november 0 Normering voor 4 pt vragen andere vragen naar rato): 4pt pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
Analyse 1 Handout limieten en continuïteit
 Analyse Handout ieten en continuïteit Rogier Bos Inhoudsopgave Limieten 2. Intuïtief ieten bepalen........................ 2.2 Rekenen aan ieten........................... 4.3 Limieten als spel.............................
Analyse Handout ieten en continuïteit Rogier Bos Inhoudsopgave Limieten 2. Intuïtief ieten bepalen........................ 2.2 Rekenen aan ieten........................... 4.3 Limieten als spel.............................
I.3 Functies. I.3.2 Voorbeeld. De afbeeldingen f: R R, x x 2 en g: R R, x x 2 zijn dus gelijk, ook al zijn ze gegeven door verschillende formules.
 I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
Centrale Commissie Voortentamen Wiskunde Uitwerkingen Voortentamen Wiskunde B 11 juni 2012
 Centrale Commissie Voortentamen Wiskunde Uitwerkingen Voortentamen Wiskunde B juni 22 Voorlopige versie 6 juni 22 Opgave a f (x) = x2 x 5, dus f (x) = 2 2 x 5x. Dit geeft f (x) = 2 2 2x3. f (x) = 2 2 2x3
Centrale Commissie Voortentamen Wiskunde Uitwerkingen Voortentamen Wiskunde B juni 22 Voorlopige versie 6 juni 22 Opgave a f (x) = x2 x 5, dus f (x) = 2 2 x 5x. Dit geeft f (x) = 2 2 2x3. f (x) = 2 2 2x3
Complexe functies. Omdat we weten hoe we complexe getallen optellen en vermenigvuldigen, hebben we met complexe functies die door een veelterm
 Wiskunde voor kunstmatige intelligentie, 5 Les 6 Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen ook
Wiskunde voor kunstmatige intelligentie, 5 Les 6 Complexe functies Nadat we de complexe getallen hebben leren kennen, is het een voor de hand liggende vraag of hiervoor net als voor de reële getallen ook
De partitieformule van Euler
 De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
en-splitsingen: een aantal alternatieven worden parallel toegepast, of-splitsingen: van een aantal alternatieven wordt er één toegepast,
 Kansrekening voor Informatiekunde, 25 Les 8 Proces analyse Veel processen laten zich door netwerken beschrijven, waarin knopen acties aangeven en opdrachten langs verbindingen tussen de knopen verwerkt
Kansrekening voor Informatiekunde, 25 Les 8 Proces analyse Veel processen laten zich door netwerken beschrijven, waarin knopen acties aangeven en opdrachten langs verbindingen tussen de knopen verwerkt
TENTAMEN ANALYSE 1. dinsdag 3 april 2007,
 TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
Hoofdstuk 3 - Transformaties
 Hoofdstuk - Transformaties Voorkennis: Standaardfuncties bladzijde 70 V-a f () = g () = sin h () = k () = log m () = n () = p () = b D f = [0, en B f = [0, ; D g = en B g =[, ] ; D h = en B h = 0, ; D
Hoofdstuk - Transformaties Voorkennis: Standaardfuncties bladzijde 70 V-a f () = g () = sin h () = k () = log m () = n () = p () = b D f = [0, en B f = [0, ; D g = en B g =[, ] ; D h = en B h = 0, ; D
Tussentoets Analyse 2. Natuur- en sterrenkunde.
 Tussentoets Analyse 2. Natuur- en sterrenkunde. Dinsdag 9 maart 2010, 9.00-11.00. Het gebruik van een rekenmachine is toegestaan. Motiveer elk antwoord dat je geeft d.m.v. een berekening of redenering.
Tussentoets Analyse 2. Natuur- en sterrenkunde. Dinsdag 9 maart 2010, 9.00-11.00. Het gebruik van een rekenmachine is toegestaan. Motiveer elk antwoord dat je geeft d.m.v. een berekening of redenering.
Standaardafgeleiden. Wisnet-HBO. update maart 2011
 Standaardafgeleiden Wisnet-HBO update maart 2011 1 Inleiding Als je nog niets over differentiëren weet, kun je beter eerst naar de les Wat is Differentiëren gaan in Wisnet Verder zijn er Maplets om de
Standaardafgeleiden Wisnet-HBO update maart 2011 1 Inleiding Als je nog niets over differentiëren weet, kun je beter eerst naar de les Wat is Differentiëren gaan in Wisnet Verder zijn er Maplets om de
Examen Complexe Analyse (September 2008)
 Examen Complexe Analyse (September 2008) De examenvragen vind je op het einde van dit documentje. Omdat het hier over weinig studenten gaat, heb ik geen puntenverdeling meegegeven. Vraag. Je had eerst
Examen Complexe Analyse (September 2008) De examenvragen vind je op het einde van dit documentje. Omdat het hier over weinig studenten gaat, heb ik geen puntenverdeling meegegeven. Vraag. Je had eerst
Voorkennis wiskunde voor Biologie, Chemie, Geografie
 Onderstaand overzicht volgt de structuur van het boek Wiskundige basisvaardigheden met bijhorende website. Per hoofdstuk wordt de strikt noodzakelijke voorkennis opgelijst: dit is leerstof die gekend wordt
Onderstaand overzicht volgt de structuur van het boek Wiskundige basisvaardigheden met bijhorende website. Per hoofdstuk wordt de strikt noodzakelijke voorkennis opgelijst: dit is leerstof die gekend wordt
Opgave a. We berekenen eerst een normaal v van V en een normaal w van W. v = (b a) (c a) = ((2)(1) ( 2)( 2), ( 2)( 1) ( 1)(1), ( 1)( 2) (2)( 1))
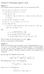 Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Functies van meer variabelen voor dummy s
 Functies van meer variabelen voor dummy s Dit is een 'praktische gids voor dummy s'. Hieronder kun je een aantal voorbeelden met uitleg vinden, oefeningen en uitwerkingen. De voorbeelden komen deels uit
Functies van meer variabelen voor dummy s Dit is een 'praktische gids voor dummy s'. Hieronder kun je een aantal voorbeelden met uitleg vinden, oefeningen en uitwerkingen. De voorbeelden komen deels uit
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 2008 Limieten en asymptoten van rationale functies (versie juli 2008) Rationale functies. Inleiding Functies als f : 5 5, f 2 : 2 3 + 2 f 3 : 32 + 7 4 en f 4 :
Katholieke Universiteit Leuven September 2008 Limieten en asymptoten van rationale functies (versie juli 2008) Rationale functies. Inleiding Functies als f : 5 5, f 2 : 2 3 + 2 f 3 : 32 + 7 4 en f 4 :
Studiewijzer Wiskunde 1 voor B(2DB00, 2DB30), cursus 2005/2006
 Studiewijzer Wiskunde 1 voor B(2DB00, 2DB30), cursus 2005/2006 Inleiding In de cursus Wiskunde 1 voor B (2DB00) wordt gebruikt het boek Calculus, Robert T. Smith, Roland B. Minton, second edition, Mc Graw
Studiewijzer Wiskunde 1 voor B(2DB00, 2DB30), cursus 2005/2006 Inleiding In de cursus Wiskunde 1 voor B (2DB00) wordt gebruikt het boek Calculus, Robert T. Smith, Roland B. Minton, second edition, Mc Graw
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 23 oktober 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 23 oktober 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
