Je draai vinden in een grote groep Rubik s Cube & Wiskunde. Prof.dr. Marko van Eekelen
|
|
|
- Brigitta van den Velde
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Je draai vinden in een grote groep Rubik s Cube & Wiskunde Prof.dr. Marko van Eekelen 22e Nationale Wiskunde Dagen, 5-6 februari /30
2 Who s that guy? Marko van Eekelen, marko.vaneekelen@ou.nl, marko@cs.ru.nl n 1981: Afgestudeerd als student KUN-Wiskunde n 2015: Nu hoogleraar Software Technologie, n Open Universiteit Nederland, Voorzitter vakgroep Informatica & Radboud Universiteit, Digital Security groep n Onderzoek: analyse van IT met wiskundige methoden n correctheid, security en energieverbruikanalyse n Maeslantkering n Slimme meters n Sovereign project n Verificatie van safety-critical software n Rijkswaterstaat, Nuclear Research Group n met Herman Geuvers, Freek Wiedijk, Sjaak Smetsers, n Maar vandaag gaat het over een andere, oude hobby van mij
3 3/ e Nationale Wiskunde Dagen, 5-6 februari /30
4 4/ e Nationale Wiskunde Dagen, 5-6 februari /30
5 5/ e Nationale Wiskunde Dagen, 5-6 februari /30
6 6/ e Nationale Wiskunde Dagen, 5-6 februari /30
7 Geschiedenis Ernö Rubik, Department of Interior Design, Academy of Applied Arts and Crafts, Boedapest n Magic Cube, eerste idee 1974, patent 1975, eerste exemplaren 1977 n Rubiks Cube, eerste industrieel export uit Hongarije, mei 1980 n 1981, David Singmaster s Cube Notes n 1981, Scientific American, D. Hofstadter n 1981, Museum of modern art, New York n 1981, Nederlandse Kubus Club (NKC) n 1982, Oxford English Dictionary n : 100 miljoen exemplaren verkocht; t/m 2008: 350 miljoen Ook in Nederland was het dé hit van 1981! De kubus komt al snel in beeld als het gaat om het jaar n Triviant (TROS), Het gevoel van (KRO), De tijd van ons leven (KRO), De televisiejaren (NCRV) 7/30
8 Wat is er zo spannend aan? n Leuke kleurtjes n Lijkt eenvoudig: beetje draaien n Binnen de kortste keren zit ie totaal in de war en kom je er niet makkelijk verder mee omdat je het effect van het draaien niet meer overziet n Maar als je goed kijkt, logisch nadenkt en gericht op zoek gaat naar manieren om kleine veranderingen te creëren, dan komt het goed. n Als je het kunt, zijn anderen onder de indruk n Je hebt dan wat om handen.. n En je kunt jezelf blijven verbeteren, n Mooie figuren, minder slagen, sneller, met je ogen dicht, met je voeten, achter je rug, en zelfs jonglerend 8/30
9 Mijn persoonlijke ervaringen n een weekend in oktober, een vakantie in december 1980, en daarna een aantal maanden erg fanatiek n 2 e bij het 1e open Draaikubuskampioenschap van Zuid-Holland, 11 juli 1981 n 1 e bij De Eerste de Beste en wereldrecord in het Guinness Book of Records (35.48 seconden), 21 aug 1981 n De huidige recordhouder lost de kubus op in minder dan 10 seconden gemiddeld! n Het wereldrecord staat nu op seconden (hyperlink). voor mensen en n iets meer dan 1 seconde (hyperlink) voor IT gestuurde apparaten n 1 e bij de Open Nederlandse Kubus Kampioenschappen, 28 aug 1981 n TV: De eerste de beste (TROS), TV-verslag van Radiokampioenschap (KRO), MIES (AVRO) 9/30
10 Kubusgekte 22e Nationale Wiskunde Dagen, 5-6 februari / /30
11 Tetraeder n Afstudeerscriptie Wiskunde 1981 n Samen met Bernard van Houtum n Op papier uitgezocht n aantal standen ( ) n oplossingsmethode n ordes (max 90), aantal standen per orde n karakterisatie van de groepsstructuur n gebruik makend van duale karakter n Geen fysieke vorm en geen computersimulatie n Geen Patent. 11/30
12 Net geen patent 12/30
13 Groepentheorie, de wiskunde van de Rubik s cube Een groep is een wiskundige structuur over objecten en bewerkingen daarop Voorbeelden van groepselementen: - Symmetrieën, spiegelingen, draaiingen (rotaties), verwisselingen (permutaties), modulo rekenen, getallen optellen Groepentheorie wordt gebruikt in: - Quantummechanica, cryptografie, kristallografie, De groep van de Rubik s Cube is heel groot. Deze groep heeft meer dan 43 triljoen elementen: /30
14 Groepen (wiskundige definitie) Zij G een verzameling met een afbeelding (de groepsoperatie) * : G x G x G (g1,g2) g1 * g2 Dan is G een groep met als groepsoperatie * d.e.s.d.a. 1. G is gesloten onder * g, h G [ g * h G ] 2. * is associatief g,h,k G [ ( g * h) * k = g * (h * k) ] 3. Er is een eenheidselement (Identiteit) Id G g G [ Id * g = g * Id = g ] 4. Elk element heeft een inverse g g g -1 G [ g * g -1 = g -1 * g = Id ] Een groep kan eindig veel elementen of oneindig veel elementen hebben 22 e Nationale Wiskunde 14/3 Dagen, 5-6 februari /30
15 Rubik s groep R (Right),L (Left),U (Up),D (Down),F (Front),B (Back) zijn draaiingen (met de klok mee als je er tegen aan kijkt) Dan is Rubik s groep, de eindige groep van alle elementen gegenereerd door combinaties van {R,L,U,D,F,B} De groepsoperatie is dan het samenstellen van (reeksen) draaiingen aan de kubus n draaiingen vormen een reeks die je in de tijd na elkaar uit kunt voeren = associatief n eenheidselement = beginstand, geen actie uitvoeren n vinden van een inverse = oplossen van een in de war gedraaide kubus n reeks draaiingen = effect op beginstand = bepaalde stand van de kubus n een aantal verwisselingen en draaiingen van blokjes 15/30
16 Even wat notatie Eerste observatie: n alles draait om de centra van de vlakken n de centra veranderen niet ten opzichte van elkaar n elk blokje heeft een eigen positie ten opzichte van de centra Notatie van de draaiingen: n Met de klok mee (als je tegen het desbetreffende centrum aankijkt) n U (up), D (down), L (left), R (right), F (front), B (back) n Tegen de klok in: n U,D,L,R,F,B n Halve slagen: n U 2,D 2,L 2,R 2,F 2,B 2 n Slices (schijven): n RL, R L, FB, 16/30
17 Een uitstapje naar slices n Slices (schijven): n R L, R L, F B, n Slices draaien is aan twee tegenoverliggende kanten voor je gevoel hetzelfde doen) n RL is hetzelfde als de middelste schijf naar voren draaien (aan beide kanten van je af) n speedcubers doen dit met 1 vinger met een gesmeerde kubus n Slices vormen een deelgroep n Met slices alleen kun je al mooie figuren maken n RL FB UD RL bijvoorbeeld levert: 17/30
18 Groepen (inverse) Inverse = het omgekeerde effect Het oplossen van de kubus komt dus eigenlijk neer op het vinden van een methode om een inverse te construeren voor een willekeurig element Stel dat je weet welke draaiingen er geweest zijn, dan is de inverse n dezelfde reeks draaiingen, in omgekeerde volgorde, elk de andere kant op draaiend n OF een andere reeks die hetzelfde effect heeft. Een notatievoorbeeld: n U -1 = U n (U 2 ) -1 = U 2 want U U = U U = Id want U 2 U 2 = Id n (L U) -1 L U want L U L U Id n (LU) -1 = U L want L U U L = L Id L = L L = Id 18/30
19 Groepen (commuteren) Commuteren = wisselen t.o.v. elkaar n Twee elementen g en h commuteren desda g * h = h * g n De commutator van g en h is g * h * g -1 * h -1 (geeft min of meer aan waarin ze niet commuteren) Als voor alle elementen van een groep geldt dat g * h = h * g dan heet de groep commutatief of abels. Je kunt dan de volgorde van de elementen van de groep omdraaien zonder dat er iets verandert n Optellen van getallen commuteert maar delen niet. n Elk groepselement commuteert met zijn inverse De groep van Rubik is niet abels. n L U U L Zomaar een commutator in de Rubik groep: L U L U 19/30
20 Eindige groepen (orde) n Elk element g uit een groep heeft een orde n waarvoor geldt: g n = 1 n Als je een reeks draaiingen maar steeds blijft herhalen kom je dus altijd weer bij de beginstand uit! n De orde van een element is altijd een deler van het aantal elementen van de groep n Orde van Rubik s groep n 8 hoekblokjes, in drie standen elk; 12 randblokjes in 2 standen elk n Met invarianten kan bewezen worden dat n randblokjes met twee tegelijk draaien, n hoekblokjes met drie tegelijk draaien (of met twee maar dan tegengesteld), n als je twee hoekblokjes verwisselt van plaats, verwisselen er ook twee randblokjes mee n De groep heeft dus (8!*3 8 *12!*2 12 )/(2*3*2) = elementen n Voorbeelden van ordes van elementen: n De orde van U is 4 want U 4 = UUUU = Id n De orde van U 2 is 2 want (U 2 ) 2 = U 2 U 2 = UUUU = Id n Er is geen element van orde 13; Max orde is 1260 (bv. R U 2 D B D ) 20/30
21 Groepen (conjugeren) Conjugeren (verbinden met, koppelen met) n De geconjugeerde van g door h is h * g * h -1 n Alle geconjugeerden van g vormen samen een equivalentieklasse (in zekere zin hebben ze allemaal hetzelfde effect) Conjugeren in de Rubik s groep is handig als je een basis operatie hebt die weinig aan de kubus verandert. Die operatie voer je ergens anders uit door te conjugeren. Bekijk in de Rubik groep (L 2 U 2 ) 3 = L 2 U 2 L 2 U 2 L 2 U 2 n (L 2 U 2 ) 3 verwisselt gelijktijdig twee randblokjes in het linkervlak (middelste laag) en in het bovenvlak (voor-achter). Dit kun je uitvoeren met de Singmaster greep: dan houd je de blokjes die verwisselen, vast tijdens het draaien. Als je nu bijvoorbeeld gelijktijdig twee randblokjes in het linkervlak (middelste laag) gelijktijdig wilt verwisselen met in het bovenvlak niet (voor-achter) maar (links-rechts) dan kun je conjugeren: n Zet de blokjes van links en rechts uit het bovenvlak zó dat ze voor en achter zitten: U n Voor de conjugatieoperatie uit: (L 2 U 2 ) 3 n Zet de blokjes in het bovenvlak weer terug: U De door U geconjugeerde van (L 2 U 2 ) 3 is daarmee dus U(L 2 U 2 ) 3 U. 21/30
22 Samenvatting van groepen n Elk element g uit een eindige groep heeft een orde n waarvoor geldt: g n = Id n is dan altijd een deler van het aantal elementen van de groep Als je een draaireeks consequent blijft herhalen komt de kubus vanzelf weer in de stand waarin je begon (na maximaal 1260 keer) n Twee elementen g en h commuteren desda g * h = h * g n De commutator van g en h is g * h * g -1 * h -1 (geeft min of meer aan waarin ze niet commuteren) n De geconjugeerde van g door h is h -1 * g * h Alle geconjugeerden van g vormen samen een equivalentieklasse (ze hebben allemaal een vergelijkbaar effect) n De kubus oplossen is het inverteren van wat iemand ermee gedaan heeft. 22/30
23 Zelf vinden van een oplossing? Combineren, Roteren, Spiegelen, Conjugeren, Commuteren, Inverteren, Orde gebruiken en misschien Demonteren. De combinatie van de twee commutatoren R U R U en U 2 R U 2 R verandert alleen iets in het bovenvlak. Met R U R U U 2 R U 2 R gecombineerd met diens gespiegelde L U L U U 2 L U 2 L heb je in het bovenvlak 2 hoeken gedraaid terwijl de rest van de kubus helemaal gelijk blijft De andere kant op draaien? n Nog een keer n Na drie keer draaien ben je weer bij het begin. n Alle draaiingen achterstevoren en de andere kant op uitvoeren 23/30
24 Verdraaid? Demonteren! Wat als je helemaal vast zit? De kubus kan uit elkaar! Draai 1 vlak zó dat het precies halverwege staat Klik met een platte schroevedraaier of beter nog: met de achterkant van een lepeltje een randblokje eruit. Peuter vervolgens een voor een de blokjes er tussen uit. Je houdt een karkas met alleen de centra over Zet alles er op de juiste plaats (!) weer terug in. Klik als laatste het randblokje er met de hand weer in Pas op: doe dit niet te vaak. Hij slijt er wel een beetje van. 24/30
25 Centrum van een groep Het centrum van een groep G is de subgroep Centrum(G) die bestaat uit die elementen van G die met alle elementen van G commuteren m.a.w: Centrum(G) = { z G z * g = g * z, g G} Een viertal eigenschappen: 1. z Centrum (G) g G [ g * z * g -1 = z ] 2. G [Id Centrum(G)] 3. Centrum (G) = G G is commutatief 4. Centrum (Rubik) = {Id, Superflip} Superflip = de operatie die elk randblokje op zijn eigen plaats draait R L U 2 F U D F 2 R 2 B 2 L U 2 F B U R 2 D F 2 U R 2 U 25/30
26 Diameter van de groep (GOD s Number) n Diameter is de langste afstand die je eventueel af zou moeten leggen als je altijd de kortste weg zou weten n met het algoritme van een alwetende god.. n Diameter tussen 18 en 52 n David Singmaster, ondergrens 18 (kwartslagen) n Morwen Thistlethwaite, bovengrens 52 n Door subgroepen heen met steeds meer halve slagen n 2010 n Diameter = 20 (met kwart en halve slagen) n Tomas Rokicki, Herbert Kociemba, Morley Davidson, and John Dethridge n 300 miljoen verste standen: bv. de superflip. n 2014 Tomas Rokicki, Morley Davidson n Diameter = 26 (alleen kwartslagen) n 29 jaar CPU-tijd, Ohio Supercomputing Centre n 1 verste stand: superflip met 4-spot 26/30
27 Wiskunde en de groep van Rubik s cube 27/2 51 n Het is een voorbeeld van een hele grote groep n Je kunt er je hele leven lang mee blijven spelen n Als je genoeg van de kubus hebt, zijn er nog heel veel varianten n In 26 kwartslagen is het theoretisch altijd te doen om de kubus weer goed te krijgen n Als je een draaireeks steeds maar herhaalt, komt alles altijd weer in orde (na maximaal 1260 keer) n Met conjugeren en commuteren kun je leren inverteren n Wiskunde helpt. (niet alleen bij de Rubik s cube) 27/30
28 28/2 51 Zelf aan de slag? Met dank aan Jumbo! 28/30
Workshop Rubik s Cube & Wiskunde
 Workshop Rubik s Cube & Wiskunde Een kleurrijke workshop 6 vierkanten voor wiskunde Vierkant voor Wiskunde Kamp B, woensdag 15 augustus 2012 Prof.dr. Marko van Eekelen, marko@cs.ru.nl 1981: Afgestudeerd
Workshop Rubik s Cube & Wiskunde Een kleurrijke workshop 6 vierkanten voor wiskunde Vierkant voor Wiskunde Kamp B, woensdag 15 augustus 2012 Prof.dr. Marko van Eekelen, marko@cs.ru.nl 1981: Afgestudeerd
De Hongaarse kubus ontward
 De Hongaarse kubus ontward door Dick Grune, Aug. 1981 herzien Febr. 2007 Er zijn vele manieren om een in de war geraakte kubus weer te ontwarren. De bekendste worden gegeven door David Singmaster en Donald
De Hongaarse kubus ontward door Dick Grune, Aug. 1981 herzien Febr. 2007 Er zijn vele manieren om een in de war geraakte kubus weer te ontwarren. De bekendste worden gegeven door David Singmaster en Donald
Uitwerkingen van geselecteerde opgaven (laatste update 4 Januari 2018) Zebra 50. De Wiskunde van Rubik s Kubus.
 Uitwerkingen van geselecteerde opgaven (laatste update 4 Januari 2018) Zebra 50. De Wiskunde van Rubik s Kubus. Opgave 1. Niet alle mogelijke posities zijn door middel van draaien te bereiken. Het is bijvoorbeeld
Uitwerkingen van geselecteerde opgaven (laatste update 4 Januari 2018) Zebra 50. De Wiskunde van Rubik s Kubus. Opgave 1. Niet alle mogelijke posities zijn door middel van draaien te bereiken. Het is bijvoorbeeld
Errata: Opgave 80: [[R,U2],D ] ipv [[R,U2],D] Opgave 87. Dit is een herhaling van opgave Deze kan geschrapt worden.
![Errata: Opgave 80: [[R,U2],D ] ipv [[R,U2],D] Opgave 87. Dit is een herhaling van opgave Deze kan geschrapt worden. Errata: Opgave 80: [[R,U2],D ] ipv [[R,U2],D] Opgave 87. Dit is een herhaling van opgave Deze kan geschrapt worden.](/thumbs/88/116941228.jpg) Errata: Opgave 80: [[R,U2],D ] ipv [[R,U2],D] Opgave 87. Dit is een herhaling van opgave 79-82. Deze kan geschrapt worden. UITWERKINGEN VAN GESELECTEERDE OPGAVEN. Opgave 1. Niet alle mogelijke posities
Errata: Opgave 80: [[R,U2],D ] ipv [[R,U2],D] Opgave 87. Dit is een herhaling van opgave 79-82. Deze kan geschrapt worden. UITWERKINGEN VAN GESELECTEERDE OPGAVEN. Opgave 1. Niet alle mogelijke posities
TIPS: PAG. 3 DES CONSEILS: PAGE 16 HINWEISE: SEITE 29
 TIPS: PAG. 3 DES CONSEILS: PAGE 16 HINWEISE: SEITE 29 00728 NL MILJARDEN COMBINATIES, EN MAAR ÉÉN OPLOSSING. Rubik s Cube is een verschrikkelijk verslavende, meerdimensionale uitdaging die puzzelfanaten
TIPS: PAG. 3 DES CONSEILS: PAGE 16 HINWEISE: SEITE 29 00728 NL MILJARDEN COMBINATIES, EN MAAR ÉÉN OPLOSSING. Rubik s Cube is een verschrikkelijk verslavende, meerdimensionale uitdaging die puzzelfanaten
Eindwerk wiskunde: De wiskunde achter de Rubik s kubus. Laurens Vanden Eynde 6 e jaar Latijn - Wiskunde
 Eindwerk wiskunde: De wiskunde achter de Rubik s kubus Laurens Vanden Eynde 6 e jaar Latijn - Wiskunde Schooljaar 2010-2011 Inhoudsopgave 1 Inleiding 2 2 Kubusnotatie 3 2.1 Design...............................
Eindwerk wiskunde: De wiskunde achter de Rubik s kubus Laurens Vanden Eynde 6 e jaar Latijn - Wiskunde Schooljaar 2010-2011 Inhoudsopgave 1 Inleiding 2 2 Kubusnotatie 3 2.1 Design...............................
Rubik s Kubus, Invarianten en bijna commuteren.
 Rubik s Kubus, Invarianten en bijna commuteren. Rubik s Kubus ziet er in de winkel uit als een kubus die verdeeld is in 27 kleine kubusjes waar gekleurde plakkertjes op zitten en wel zo dat de negen plakkertjes
Rubik s Kubus, Invarianten en bijna commuteren. Rubik s Kubus ziet er in de winkel uit als een kubus die verdeeld is in 27 kleine kubusjes waar gekleurde plakkertjes op zitten en wel zo dat de negen plakkertjes
SYMMETRIEËN VAN RUIMTELIJKE FIGUREN. Prof. dr. Ronald Meester
 SYMMETRIEËN VAN RUIMTELIJKE FIGUREN Prof. dr. Ronald Meester Inleiding In dit college onderzoeken we symmetrie-eigenschappen van ruimtelijke figuren zoals driehoeken, vierkanten, kubussen en andere veelvlakken
SYMMETRIEËN VAN RUIMTELIJKE FIGUREN Prof. dr. Ronald Meester Inleiding In dit college onderzoeken we symmetrie-eigenschappen van ruimtelijke figuren zoals driehoeken, vierkanten, kubussen en andere veelvlakken
5 Inleiding tot de groepentheorie
 5 Inleiding tot de groepentheorie Oefening 5.1. Stel de Cayleytabel op voor de groep van de symmetrieën van een vierkant. Bewijs dat deze groep de viergroep van Klein bezit als deelgroep van index 2. Oplossing
5 Inleiding tot de groepentheorie Oefening 5.1. Stel de Cayleytabel op voor de groep van de symmetrieën van een vierkant. Bewijs dat deze groep de viergroep van Klein bezit als deelgroep van index 2. Oplossing
Revenge De ultieme uitdaging 2. Even voorstellen: Revenge 3. Algemene tips 8. Draaipatronen bij Revenge 19. Oplossen van Rubik s Revenge 28
 Rubik s Revenge Revenge De ultieme uitdaging 2 Even voorstellen: Revenge 3 Draaitips 5 Algemene tips 8 Notatiesysteem 12 Draaipatronen bij Revenge 19 Oplossen van Rubik s Revenge 28 Er is meer Revenge
Rubik s Revenge Revenge De ultieme uitdaging 2 Even voorstellen: Revenge 3 Draaitips 5 Algemene tips 8 Notatiesysteem 12 Draaipatronen bij Revenge 19 Oplossen van Rubik s Revenge 28 Er is meer Revenge
De algemeen gebruikte notatie:
 Makkelijke oplossing voor Rubik's Kubus Deze oplossing vergt niet zoveel leeswerk. Kijk bij elke stap wat het doel is, en welke algoritmes er gebruikt worden om dat doel te bereiken. Soms moet je een algoritme
Makkelijke oplossing voor Rubik's Kubus Deze oplossing vergt niet zoveel leeswerk. Kijk bij elke stap wat het doel is, en welke algoritmes er gebruikt worden om dat doel te bereiken. Soms moet je een algoritme
De draaikubus van Rubik Joost Hulshof
 De draaikubus van Rubik Joost Hulshof 20-4-2007 Er zijn vele variaties van de draaikubus van Rubik, maar de eerste blijft de mooiste. De 3x3x3 kubus kwam op de markt toen ik derdejaarsstudent was in Leiden.
De draaikubus van Rubik Joost Hulshof 20-4-2007 Er zijn vele variaties van de draaikubus van Rubik, maar de eerste blijft de mooiste. De 3x3x3 kubus kwam op de markt toen ik derdejaarsstudent was in Leiden.
Local Moufang sets. Erik Rijcken. Promotor: Prof. Dr. Tom De Medts. Faculteit Wetenschappen Universiteit Gent 14 juni 2017
 µ xµy M(U, τ) Local Moufang sets x Erik Rijcken Promotor: Prof. Dr. Tom De Medts U HτU Faculteit Wetenschappen Universiteit Gent 4 juni 207 Overzicht Groepsacties: symmetrie gebruiken 2 Moufang sets Velden
µ xµy M(U, τ) Local Moufang sets x Erik Rijcken Promotor: Prof. Dr. Tom De Medts U HτU Faculteit Wetenschappen Universiteit Gent 4 juni 207 Overzicht Groepsacties: symmetrie gebruiken 2 Moufang sets Velden
Werkwinkel Permutatiepuzzels
 Werkwinkel Permutatiepuzzels Karsten Naert UGent Vakgroep Wiskunde 6 november 2013 1 / 33 Over mij... Assistent en doctoraatsstudent Taken: Onderzoek Onderwijs Dienstverlening Karsten.Naert@UGent.be http:
Werkwinkel Permutatiepuzzels Karsten Naert UGent Vakgroep Wiskunde 6 november 2013 1 / 33 Over mij... Assistent en doctoraatsstudent Taken: Onderzoek Onderwijs Dienstverlening Karsten.Naert@UGent.be http:
Morenaments Ornamenten met symmetrie. Werkblad vooraf met begeleidende tekst en oplossingen
 Morenaments Ornamenten met symmetrie Fien Aelter, Liesje Knaepen en Kristien Vanhuyse, studenten SLO wiskunde KU Leuven Werkblad vooraf met begeleidende tekst en oplossingen Dit werklad is een voorbereiding
Morenaments Ornamenten met symmetrie Fien Aelter, Liesje Knaepen en Kristien Vanhuyse, studenten SLO wiskunde KU Leuven Werkblad vooraf met begeleidende tekst en oplossingen Dit werklad is een voorbereiding
Workshop Permutatiepuzzels
 Workshop Permutatiepuzzels Karsten Naert UGent Vakgroep Wiskunde January 26, 2012 Wiskunde is: Abstractie maken van de werkelijkheid Redeneren met deze abstracte gegevens (Zie ook: http://www.wiskunde.ugent.be/kiezen/wat.php)
Workshop Permutatiepuzzels Karsten Naert UGent Vakgroep Wiskunde January 26, 2012 Wiskunde is: Abstractie maken van de werkelijkheid Redeneren met deze abstracte gegevens (Zie ook: http://www.wiskunde.ugent.be/kiezen/wat.php)
De Wiskunde van de Rubik s Kubus
 De Wiskunde van de Rubik s Kubus door Leroy Soesman Copyright 2015 Leroy Soesman ! 2 De Wiskunde van De Rubik s Kubus Geschreven door Leroy Soesman Docent Wiskunde aan het ROC Nova College te Haarlem en
De Wiskunde van de Rubik s Kubus door Leroy Soesman Copyright 2015 Leroy Soesman ! 2 De Wiskunde van De Rubik s Kubus Geschreven door Leroy Soesman Docent Wiskunde aan het ROC Nova College te Haarlem en
Tentamen algebra 1 Woensdag 24 juni 2015, 10:00 13:00 Snelliusgebouw B1 (extra tijd), B2, B3, 312
 Tentamen algebra 1 Woensdag 24 juni 2015, 10:00 13:00 Snelliusgebouw B1 (extra tijd), B2, B3, 312 Je mag de syllabus en aantekeningen gebruiken, maar geen rekenmachine. Je mag opgaven 2.46, 2.49 en 8.13
Tentamen algebra 1 Woensdag 24 juni 2015, 10:00 13:00 Snelliusgebouw B1 (extra tijd), B2, B3, 312 Je mag de syllabus en aantekeningen gebruiken, maar geen rekenmachine. Je mag opgaven 2.46, 2.49 en 8.13
Polyatheorie. Erik Verraedt 2011-2012
 2011-2012 Inhoudsopgave 1 Inleiding 4 2 Enkele telproblemen 5 2.1 Probleem 1........................................ 5 2.2 Probleem 2........................................ 5 2.3 Probleem 3........................................
2011-2012 Inhoudsopgave 1 Inleiding 4 2 Enkele telproblemen 5 2.1 Probleem 1........................................ 5 2.2 Probleem 2........................................ 5 2.3 Probleem 3........................................
Deelgroepen en normaaldelers
 Hoofdstuk 2 Deelgroepen en normaaldelers 2.1 Wat is een deelgroep? Definitie 2.1. Een deelverzameling H van een groep G, is een deelgroep van G als en slechts als H niet leeg is en H, zelf een groep is.
Hoofdstuk 2 Deelgroepen en normaaldelers 2.1 Wat is een deelgroep? Definitie 2.1. Een deelverzameling H van een groep G, is een deelgroep van G als en slechts als H niet leeg is en H, zelf een groep is.
Hoofdstuk 1. Inleiding. Lichamen
 Hoofdstuk 1 Lichamen Inleiding In Lineaire Algebra 1 en 2 heb je al kennis gemaakt met de twee belangrijkste begrippen uit de lineaire algebra: vectorruimte en lineaire afbeelding. In dit hoofdstuk gaan
Hoofdstuk 1 Lichamen Inleiding In Lineaire Algebra 1 en 2 heb je al kennis gemaakt met de twee belangrijkste begrippen uit de lineaire algebra: vectorruimte en lineaire afbeelding. In dit hoofdstuk gaan
De WrapSlide-puzzel algebraïsch bekeken. Dimitri Geelhoed en Lotte Meester 2013
 De WrapSlide-puzzel algebraïsch bekeken Dimitri Geelhoed en Lotte Meester 2013 1 Inleiding Al snel nadat we besloten om onderzoek te doen naar een wiskundig vraagstuk, kregen we het idee om een puzzel
De WrapSlide-puzzel algebraïsch bekeken Dimitri Geelhoed en Lotte Meester 2013 1 Inleiding Al snel nadat we besloten om onderzoek te doen naar een wiskundig vraagstuk, kregen we het idee om een puzzel
Ziet uw kubus er op dit moment niet zo uit? Maar wilt u hem wel zo krijgen? Dan zit u hier goed!
 Ziet uw kubus er op dit moment niet zo uit? Maar wilt u hem wel zo krijgen? Dan zit u hier goed! Stap voor stap uitgelegd hoe u uw kubus van Rubik weer goed krijgt. Orginele versie http://rubik.tormentil.nl/
Ziet uw kubus er op dit moment niet zo uit? Maar wilt u hem wel zo krijgen? Dan zit u hier goed! Stap voor stap uitgelegd hoe u uw kubus van Rubik weer goed krijgt. Orginele versie http://rubik.tormentil.nl/
Universiteit Gent. Academiejaar Discrete Wiskunde. 1ste kandidatuur Informatica. Collegenota s. Prof. Dr.
 Universiteit Gent Academiejaar 2001 2002 Discrete Wiskunde 1ste kandidatuur Informatica Collegenota s Prof. Dr. Frank De Clerck Herhalingsoefeningen 1. Bepaal het quotiënt en de rest van de deling van
Universiteit Gent Academiejaar 2001 2002 Discrete Wiskunde 1ste kandidatuur Informatica Collegenota s Prof. Dr. Frank De Clerck Herhalingsoefeningen 1. Bepaal het quotiënt en de rest van de deling van
Ter Leering ende Vermaeck
 Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Algebra. Oefeningen op hoofdstuk Groepentheorie Cayleytabellen van groepen van orde Cyclische groepen
 Oefeningen op hoofdstuk 5 Algebra 5.2 Groepentheorie 5.2.1 Cayleytabellen van groepen van orde 8 Oefening 5.1. Stel de Cayleytabel op voor de groep van de symmetrieën van een vierkant. Bewijs dat deze
Oefeningen op hoofdstuk 5 Algebra 5.2 Groepentheorie 5.2.1 Cayleytabellen van groepen van orde 8 Oefening 5.1. Stel de Cayleytabel op voor de groep van de symmetrieën van een vierkant. Bewijs dat deze
Lineaire afbeeldingen
 Les 2 Lineaire afbeeldingen Als een robot bij de robocup (het voetbaltoernooi voor robots een doelpunt wil maken moet hij eerst in de goede positie komen, d.w.z. geschikt achter de bal staan. Hiervoor
Les 2 Lineaire afbeeldingen Als een robot bij de robocup (het voetbaltoernooi voor robots een doelpunt wil maken moet hij eerst in de goede positie komen, d.w.z. geschikt achter de bal staan. Hiervoor
Public Key Cryptography. Wieb Bosma
 Public Key Cryptography de wiskunde van het perfecte kopje koffie Wieb Bosma Radboud Universiteit Nijmegen Bachelordag 2 april 2011 Nijmegen, 6 november 2010 0 Nijmegen, 6 november 2010 1 cryptografie
Public Key Cryptography de wiskunde van het perfecte kopje koffie Wieb Bosma Radboud Universiteit Nijmegen Bachelordag 2 april 2011 Nijmegen, 6 november 2010 0 Nijmegen, 6 november 2010 1 cryptografie
Van groepentheorie tot Rubiks kubus
 Van groepentheorie tot Rubiks kubus Inneke Van Gelder ivgelder@vub.ac.be Inleiding We zullen volgende notaties gebruiken: N de verzameling van natuurlijke getallen, Z de verzameling van gehele getallen,
Van groepentheorie tot Rubiks kubus Inneke Van Gelder ivgelder@vub.ac.be Inleiding We zullen volgende notaties gebruiken: N de verzameling van natuurlijke getallen, Z de verzameling van gehele getallen,
Definitie 4.1. Als H en K normaaldelers zijn van een groep G en H K = {e} en HK = G dan noemt men G het direct product van
 Hoofdstuk 4 Groepsconstructies 4.1 Direct product We gaan nu bestuderen hoe we van 2 groepen een nieuwe groep kunnen maken of hoe we een groep kunnen schrijven als een product van 2 groepen met kleinere
Hoofdstuk 4 Groepsconstructies 4.1 Direct product We gaan nu bestuderen hoe we van 2 groepen een nieuwe groep kunnen maken of hoe we een groep kunnen schrijven als een product van 2 groepen met kleinere
Transformaties van grafieken HAVO wiskunde B deel 2. Willem van Ravenstein Haags Montessori Lyceum (c) 2016
 Transformaties van grafieken HAVO wiskunde B deel Willem van Ravenstein 50075005 Haags Montessori Lyceum (c) 0 Inleiding In deze leerroute gaan we kijken naar goniometrische functies: De eenheidscirkel
Transformaties van grafieken HAVO wiskunde B deel Willem van Ravenstein 50075005 Haags Montessori Lyceum (c) 0 Inleiding In deze leerroute gaan we kijken naar goniometrische functies: De eenheidscirkel
Opgave 1 Bepaal welke van de volgende beweringen juist zijn: = Z2 Z 6 (R >0, ) = (R, +) (Z, +) = (Q, +)
 Deeltentamen Groepentheorie (WISB221). A. Henriques, Nov 2012. Geef niet alleen anwoorden, maar bewijs al je beweringen. Opgave 1 Bepaal welke van de volgende beweringen juist zijn: [5pt] Z 5 = Z 4, Z
Deeltentamen Groepentheorie (WISB221). A. Henriques, Nov 2012. Geef niet alleen anwoorden, maar bewijs al je beweringen. Opgave 1 Bepaal welke van de volgende beweringen juist zijn: [5pt] Z 5 = Z 4, Z
Definitie 1.1. Een groep is een verzameling G, uitgerust met een bewerking waarvoor geldt dat:
 Hoofdstuk 1 Eerste begrippen 1.1 Wat is een groep? Definitie 1.1. Een groep is een verzameling G, uitgerust met een bewerking waarvoor geldt dat: 1. a, b G : a b G 2. a, b, c G : a (b c) = (a b) c = a
Hoofdstuk 1 Eerste begrippen 1.1 Wat is een groep? Definitie 1.1. Een groep is een verzameling G, uitgerust met een bewerking waarvoor geldt dat: 1. a, b G : a b G 2. a, b, c G : a (b c) = (a b) c = a
Verzamelingen deel 3. Derde college
 1 Verzamelingen deel 3 Derde college rekenregels Een bewerking op A heet commutatief als voor alle x en y in A geldt dat x y = y x. Een bewerking op A heet associatief als voor alle x, y en z in A geldt
1 Verzamelingen deel 3 Derde college rekenregels Een bewerking op A heet commutatief als voor alle x en y in A geldt dat x y = y x. Een bewerking op A heet associatief als voor alle x, y en z in A geldt
2008 1 e ronde Klas 3 4
 2008 1 e ronde Klas 3 4 Html Vraag Scoretype A Ondeugende bevers Beverpaden Beverpod Drie werkers Letters wisselen Auto's Kortste pad Hoeveel studenten A A A A B B B B Tafel dekken B Stapels kaarten splitsen
2008 1 e ronde Klas 3 4 Html Vraag Scoretype A Ondeugende bevers Beverpaden Beverpod Drie werkers Letters wisselen Auto's Kortste pad Hoeveel studenten A A A A B B B B Tafel dekken B Stapels kaarten splitsen
5.2.4 Varia in groepentheorie
 Oefeningen op hoofdstuk 5 Algebra 5.2 Groepentheorie 5.2.1 Cayleytabellen van groepen van orde 8 Oefening 5.1. Stel de Cayleytabel op voor de groep van de symmetrieën van een vierkant. Bewijs dat deze
Oefeningen op hoofdstuk 5 Algebra 5.2 Groepentheorie 5.2.1 Cayleytabellen van groepen van orde 8 Oefening 5.1. Stel de Cayleytabel op voor de groep van de symmetrieën van een vierkant. Bewijs dat deze
HOEKENWERK WISKUNDE GEHELE GETALLEN
 Hoekenwerk NAAM: NR:. KLAS: 1A HOEKENWERK WISKUNDE GEHELE GETALLEN Bij dit hoekenwerk doorloop je in een bepaalde volgorde de volgende hoeken: 1. Bewerkingen met gehele getallen 2. Getallenlijn en coördinaten
Hoekenwerk NAAM: NR:. KLAS: 1A HOEKENWERK WISKUNDE GEHELE GETALLEN Bij dit hoekenwerk doorloop je in een bepaalde volgorde de volgende hoeken: 1. Bewerkingen met gehele getallen 2. Getallenlijn en coördinaten
Gehelen van Gauss. Hector Mommaerts
 Gehelen van Gauss Hector Mommaerts 2 Hoofdstuk 1 Definities Gehelen van Gauss zijn complexe getallen van de vorm a + bi waarbij a, b Z. De verzameling van alle gehelen van Gauss noteren we met Z(i). Dus
Gehelen van Gauss Hector Mommaerts 2 Hoofdstuk 1 Definities Gehelen van Gauss zijn complexe getallen van de vorm a + bi waarbij a, b Z. De verzameling van alle gehelen van Gauss noteren we met Z(i). Dus
Het eenzame vierkant van Khajuraho!
 Het eenzame vierkant van Khajuraho! Stephan Berendonk 19-12-2006 ii Contents 1 De Lo Shu vii 2 Het vierkant van Khajuraho xi iv Contents Voorwoord Het stuk is vooral gericht op middelbare scholieren, die
Het eenzame vierkant van Khajuraho! Stephan Berendonk 19-12-2006 ii Contents 1 De Lo Shu vii 2 Het vierkant van Khajuraho xi iv Contents Voorwoord Het stuk is vooral gericht op middelbare scholieren, die
Cryptografie met krommen. Reinier Bröker. Universiteit Leiden
 Cryptografie met krommen Reinier Bröker Universiteit Leiden Nationale Wiskundedagen Februari 2006 Cryptografie Cryptografie gaat over geheimschriften en het versleutelen van informatie. Voorbeelden. Klassieke
Cryptografie met krommen Reinier Bröker Universiteit Leiden Nationale Wiskundedagen Februari 2006 Cryptografie Cryptografie gaat over geheimschriften en het versleutelen van informatie. Voorbeelden. Klassieke
Groepen, ringen en velden
 Groepen, ringen en velden Groep Een groep G is een verzameling van elementen en een binaire operator met volgende eigenschappen: 1. closure (gesloten): als a en b tot G behoren, doet a b dat ook. 2. associativiteit:
Groepen, ringen en velden Groep Een groep G is een verzameling van elementen en een binaire operator met volgende eigenschappen: 1. closure (gesloten): als a en b tot G behoren, doet a b dat ook. 2. associativiteit:
Inleiding tot groepentheorie
 Hoofdstuk Inleiding tot groepentheorie 1 Basisdefinities Een algebraïsche structuur bestaat meestal uit een verzameling waarop één of meerdere bewerkingen gedefinieerd zijn. Definitie Een inwendige bewerking
Hoofdstuk Inleiding tot groepentheorie 1 Basisdefinities Een algebraïsche structuur bestaat meestal uit een verzameling waarop één of meerdere bewerkingen gedefinieerd zijn. Definitie Een inwendige bewerking
We beginnen met de eigenschappen van de gehele getallen.
 II.2 Gehele getallen We beginnen met de eigenschappen van de gehele getallen. Axioma s voor Z De gegevens zijn: (a) een verzameling Z; (b) elementen 0 en 1 in Z; (c) een afbeelding +: Z Z Z, de optelling;
II.2 Gehele getallen We beginnen met de eigenschappen van de gehele getallen. Axioma s voor Z De gegevens zijn: (a) een verzameling Z; (b) elementen 0 en 1 in Z; (c) een afbeelding +: Z Z Z, de optelling;
Bruno Ernst Symposium
 Bruno Ernst Symposium Betegelingen en behanggroepen symmetrie in wiskundige termen Jeanine Daems Universiteit Leiden Voorbeelden van symmetrische figuren: wat is symmetrie in de wiskunde? symmetrie
Bruno Ernst Symposium Betegelingen en behanggroepen symmetrie in wiskundige termen Jeanine Daems Universiteit Leiden Voorbeelden van symmetrische figuren: wat is symmetrie in de wiskunde? symmetrie
Stratifications on moduli spaces of abelian varieties and Deligne-Lusztig varieties
 UvA-DARE (Digital Academic Repository) Stratifications on moduli spaces of abelian varieties and Deligne-Lusztig varieties Hoeve, M.C. Link to publication Citation for published version (APA): Hoeve, M.
UvA-DARE (Digital Academic Repository) Stratifications on moduli spaces of abelian varieties and Deligne-Lusztig varieties Hoeve, M.C. Link to publication Citation for published version (APA): Hoeve, M.
ALGEBRA I. P. Stevenhagen
 ALGEBRA I P. Stevenhagen 2015 INHOUDSOPGAVE ALGEBRA I 1. Wat is algebra? 7 Groepen, ringen en lichamen Symmetrieën van de ruit Rekenen modulo 8 Symmetrieën van het vierkant Permutaties van 4 elementen
ALGEBRA I P. Stevenhagen 2015 INHOUDSOPGAVE ALGEBRA I 1. Wat is algebra? 7 Groepen, ringen en lichamen Symmetrieën van de ruit Rekenen modulo 8 Symmetrieën van het vierkant Permutaties van 4 elementen
Het karakteristieke polynoom
 Hoofdstuk 6 Het karakteristieke polynoom We herhalen eerst kort de definities van eigenwaarde en eigenvector, nu in een algemene vectorruimte Definitie 6 Een eigenvector voor een lineaire transformatie
Hoofdstuk 6 Het karakteristieke polynoom We herhalen eerst kort de definities van eigenwaarde en eigenvector, nu in een algemene vectorruimte Definitie 6 Een eigenvector voor een lineaire transformatie
Samenvatting in het nederlands
 Samenvatting in het nederlands Wat voorkennis Stel dat van een oppervlak in de ruimte een golffront komt - het kan om licht gaan, of om geluid. Is het oppervlak een ellipsoide en breidt de golf zich uit
Samenvatting in het nederlands Wat voorkennis Stel dat van een oppervlak in de ruimte een golffront komt - het kan om licht gaan, of om geluid. Is het oppervlak een ellipsoide en breidt de golf zich uit
Uitwerking vierde serie inleveropgaven
 Uitwerking vierde serie inleveropgaven Opgave 1. Gegeven is dat G een permutatiegroep is; a is een willekeurig element. St(a) is de deelverzameling van G die alle permutaties π bevat waarvoor geldt π(a)
Uitwerking vierde serie inleveropgaven Opgave 1. Gegeven is dat G een permutatiegroep is; a is een willekeurig element. St(a) is de deelverzameling van G die alle permutaties π bevat waarvoor geldt π(a)
RSA. F.A. Grootjen. 8 maart 2002
 RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
Rekenen: Meten groep 4 en hoger. Het leren van simpele weegopdrachten.
 Activiteit 7 Lichtste en zwaarste Sorteer algoritmes Samenvatting Computers worden vaak gebruikt om lijsten in een bepaalde volgorde te zetten, bijvoorbeeld namen in alfabetische volgorde, e-mails of afspraken
Activiteit 7 Lichtste en zwaarste Sorteer algoritmes Samenvatting Computers worden vaak gebruikt om lijsten in een bepaalde volgorde te zetten, bijvoorbeeld namen in alfabetische volgorde, e-mails of afspraken
Definitie 5.1. Cyclische groepen zijn groepen voortgebracht door 1 element.
 Hoofdstuk 5 Cyclische groepen 5.1 Definitie Definitie 5.1. Cyclische groepen zijn groepen voortgebracht door 1 element. Als G wordt voortgebracht door a en a n = e, dan noteren we de groep als C n = a.
Hoofdstuk 5 Cyclische groepen 5.1 Definitie Definitie 5.1. Cyclische groepen zijn groepen voortgebracht door 1 element. Als G wordt voortgebracht door a en a n = e, dan noteren we de groep als C n = a.
II.3 Equivalentierelaties en quotiënten
 II.3 Equivalentierelaties en quotiënten Een belangrijk begrip in de wiskunde is het begrip relatie. Een relatie op een verzameling is een verband tussen twee elementen uit die verzameling waarbij de volgorde
II.3 Equivalentierelaties en quotiënten Een belangrijk begrip in de wiskunde is het begrip relatie. Een relatie op een verzameling is een verband tussen twee elementen uit die verzameling waarbij de volgorde
College WisCKI. Albert Visser. 10 oktober, Department of Philosophy, Faculty Humanities, Utrecht University. Equivalentierelaties.
 College WisCKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 10 oktober, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Wat is een equivalentierelatie? Een equivalentie
College WisCKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 10 oktober, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Wat is een equivalentierelatie? Een equivalentie
Hoofdstuk 6. Dihedrale groepen. 6.1 Definitie
 Hoofdstuk 6 Dihedrale groepen 6.1 Definitie Definitie 6.1. De dihaeder groep is de symmetriegroep van een regelmatige n-hoek. Dit is de verzameling van alle transformaties in het vlak die de regelmatige
Hoofdstuk 6 Dihedrale groepen 6.1 Definitie Definitie 6.1. De dihaeder groep is de symmetriegroep van een regelmatige n-hoek. Dit is de verzameling van alle transformaties in het vlak die de regelmatige
Platonische transformatiegroepen
 Platonische transformatiegroepen Luc Van den Broeck 8 augustus 2015 Samenvatting In dit document worden de transformatiegroepen van de platonische lichamen bestudeerd. Zonder te vervallen in algebraïsche
Platonische transformatiegroepen Luc Van den Broeck 8 augustus 2015 Samenvatting In dit document worden de transformatiegroepen van de platonische lichamen bestudeerd. Zonder te vervallen in algebraïsche
te vermenigvuldigen, waarbij N het aantal geslagen Nederlandse munten en B het aantal geslagen buitenlandse munten zijn. Het resultaat is de vector
 Les 3 Matrix product We hebben gezien hoe we matrices kunnen gebruiken om lineaire afbeeldingen te beschrijven. Om het beeld van een vector onder een afbeelding te bepalen hebben we al een soort product
Les 3 Matrix product We hebben gezien hoe we matrices kunnen gebruiken om lineaire afbeeldingen te beschrijven. Om het beeld van een vector onder een afbeelding te bepalen hebben we al een soort product
Algoritmes en Priemgetallen. Hoe maak je een sleutelpaar voor RSA?
 Algoritmes en Priemgetallen Hoe maak je een sleutelpaar voor RSA? Het recept van RSA Kies p q priemgetallen en bepaal N = pq Kies e Z N (publieke sleutel) Bepaal d e 1 mod φ N (privésleutel) x ed x kφ
Algoritmes en Priemgetallen Hoe maak je een sleutelpaar voor RSA? Het recept van RSA Kies p q priemgetallen en bepaal N = pq Kies e Z N (publieke sleutel) Bepaal d e 1 mod φ N (privésleutel) x ed x kφ
Algoritmes in ons dagelijks leven. Leve de Wiskunde! 7 April 2017 Jacobien Carstens
 Algoritmes in ons dagelijks leven Leve de Wiskunde! 7 April 2017 Jacobien Carstens Wat is een algoritme? Een algoritme is een eindige reeks instructies die vanuit een gegeven begintoestand naar een beoogd
Algoritmes in ons dagelijks leven Leve de Wiskunde! 7 April 2017 Jacobien Carstens Wat is een algoritme? Een algoritme is een eindige reeks instructies die vanuit een gegeven begintoestand naar een beoogd
Origami Meetkunde. Peter Lombaers en Jan-Willem Tel 26 mei 2011
 Origami Meetkunde Peter Lombaers en Jan-Willem Tel 26 mei 2011 Samenvatting In dit dictaat beschouwen we een manier om hoeken en afstanden te construeren: origami. We vergelijken het met het construeren
Origami Meetkunde Peter Lombaers en Jan-Willem Tel 26 mei 2011 Samenvatting In dit dictaat beschouwen we een manier om hoeken en afstanden te construeren: origami. We vergelijken het met het construeren
Sterrenwerk. Rekenen. voor 9-11 jaar. combineren en visualiseren 2
 Sterrenwerk Rekenen voor 9-11 jaar combineren en visualiseren 2 2 Hexomino s 1 Die dekselse figuren van zes! Deze figuren bestaan uit zes vierkanten die elkaar met ten minste een zijde raken. Ze heten
Sterrenwerk Rekenen voor 9-11 jaar combineren en visualiseren 2 2 Hexomino s 1 Die dekselse figuren van zes! Deze figuren bestaan uit zes vierkanten die elkaar met ten minste een zijde raken. Ze heten
Wisknutselen in de klas: creatief met wiskunde
 Wisknutselen in de klas: creatief met wiskunde Florine Meijer, Wisknutsels Inleiding Creativiteit en wiskunde, gaat dat samen? Kan je wiskunde doen en tegelijk knippen en plakken, of haken, breien en borduren?
Wisknutselen in de klas: creatief met wiskunde Florine Meijer, Wisknutsels Inleiding Creativiteit en wiskunde, gaat dat samen? Kan je wiskunde doen en tegelijk knippen en plakken, of haken, breien en borduren?
1 Symmetrieën van figuren
 1 Symmetrieën van figuren 1.1 Het mysterie van de hoge eik Als je door een met water gevulde reageerbuis heen de woorden DIE HOHE EICHE FÄLLT LANGSAM UM leest, waarbij de eerste drie woorden rood en de
1 Symmetrieën van figuren 1.1 Het mysterie van de hoge eik Als je door een met water gevulde reageerbuis heen de woorden DIE HOHE EICHE FÄLLT LANGSAM UM leest, waarbij de eerste drie woorden rood en de
D-dag 2014 Vrijeschool Zutphen VO. D -DAG 13 februari 2014: 1+ 1 = 2. (en hoe nu verder?) 1 = 2en hoe nu verder?
 D -DAG 13 februari 2014: 1+ 1 = 2 (en hoe nu verder?) 1 = 2en hoe nu verder? 1 Inleiding Snel machtsverheffen Stel je voor dat je 7 25 moet uitrekenen. Je weet dat machtsverheffen herhaald vermenigvuldigen
D -DAG 13 februari 2014: 1+ 1 = 2 (en hoe nu verder?) 1 = 2en hoe nu verder? 1 Inleiding Snel machtsverheffen Stel je voor dat je 7 25 moet uitrekenen. Je weet dat machtsverheffen herhaald vermenigvuldigen
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dystra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 12 februari 2008 INLEIDING Discrete Structuren Wee1: Inleiding Onderwerpen
Discrete Structuren Piter Dystra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 12 februari 2008 INLEIDING Discrete Structuren Wee1: Inleiding Onderwerpen
Uitleg. Welkom bij de Beverwedstrijd 2006. Je krijgt 15 vragen, die je in maximaal 45 minuten moet beantwoorden.
 Uitleg Welkom bij de Beverwedstrijd 2006 Je krijgt 15 vragen, die je in maximaal 45 minuten moet beantwoorden. Je krijgt 5 vragen van niveau A, 5 vragen van niveau B en 5 vragen van niveau C. Wij denken
Uitleg Welkom bij de Beverwedstrijd 2006 Je krijgt 15 vragen, die je in maximaal 45 minuten moet beantwoorden. Je krijgt 5 vragen van niveau A, 5 vragen van niveau B en 5 vragen van niveau C. Wij denken
WISKUNDE B -DAG 2002 1+ 1 = 2. maar en hoe nu verder? 29 november 2002
 - 0 - WISKUNDE B -DAG 2002 1+ 1 = 2 maar en hoe nu verder? 29 november 2002 De Wiskunde B-dag wordt gesponsord door Texas Instruments - 1 - Inleiding Snel machtverheffen Stel je voor dat je 7 25 moet uitrekenen.
- 0 - WISKUNDE B -DAG 2002 1+ 1 = 2 maar en hoe nu verder? 29 november 2002 De Wiskunde B-dag wordt gesponsord door Texas Instruments - 1 - Inleiding Snel machtverheffen Stel je voor dat je 7 25 moet uitrekenen.
Nu een leuk stukje wiskunde ter vermaak (hoop ik dan maar). Optellen van oneindig veel getallen
 Nu een leuk stukje wiskunde ter vermaak (hoop ik dan maar). Optellen van oneindig veel getallen Ter inleiding: tellen Turven, maar: onhandig bij grote aantallen. Romeinse cijfers: speciale symbolen voor
Nu een leuk stukje wiskunde ter vermaak (hoop ik dan maar). Optellen van oneindig veel getallen Ter inleiding: tellen Turven, maar: onhandig bij grote aantallen. Romeinse cijfers: speciale symbolen voor
Wiskunde voor relativiteitstheorie
 Wiskunde voor relativiteitstheorie HOVO Utrecht Les 1: Goniometrie en vectoren Dr. Harm van der Lek vdlek@vdlek.nl Natuurkunde hobbyist Overzicht colleges 1. College 1 1. Goniometrie 2. Vectoren 2. College
Wiskunde voor relativiteitstheorie HOVO Utrecht Les 1: Goniometrie en vectoren Dr. Harm van der Lek vdlek@vdlek.nl Natuurkunde hobbyist Overzicht colleges 1. College 1 1. Goniometrie 2. Vectoren 2. College
College WisCKI. Albert Visser. 16 januari, Department of Philosophy, Faculty Humanities, Utrecht University. Loodrechte Projectie
 College WisCKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 16 januari, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Zij V een deelruimte met basis v 1,..., v k.
College WisCKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 16 januari, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Zij V een deelruimte met basis v 1,..., v k.
14 Slotopdrachten dimensionale partities Priempartities Gekleurde partities n-gonale getallen
 4 Slotopdrachten Voor de afronding van de lessen reeks Combinatoriek en Partities is het de bedoeling dat jullie in groepjes van twee een werkstuk maken over één van de onderwerpen die in dit hoofdstuk
4 Slotopdrachten Voor de afronding van de lessen reeks Combinatoriek en Partities is het de bedoeling dat jullie in groepjes van twee een werkstuk maken over één van de onderwerpen die in dit hoofdstuk
Rekentijger - Groep 7 Tips bij werkboekje A
 Rekentijger - Groep 7 Tips bij werkboekje A Omtrek en oppervlakte (1) Werkblad 1 Van een rechthoek die mooi in het rooster past zijn lengte en breedte hele getallen. Lengte en breedte zijn samen gelijk
Rekentijger - Groep 7 Tips bij werkboekje A Omtrek en oppervlakte (1) Werkblad 1 Van een rechthoek die mooi in het rooster past zijn lengte en breedte hele getallen. Lengte en breedte zijn samen gelijk
Herhaling. Individuele Oefening. Individuele oefening. Tips en technieken in Alice. Vis in de zee Houdt van zeewier
 Herhaling Individuele Oefening Klasseniveaumethode Voorbeeld Overerving Object erft methodes van eerder gedefinieerd object Voorbeeld Object opslaan onder nieuwe naam. Latere instantie kunnen vroeger gedefinieerde
Herhaling Individuele Oefening Klasseniveaumethode Voorbeeld Overerving Object erft methodes van eerder gedefinieerd object Voorbeeld Object opslaan onder nieuwe naam. Latere instantie kunnen vroeger gedefinieerde
Magidoku s en verborgen symmetrieën
 Uitwerking Puzzel 92-6 Magidoku s en verborgen symmetrieën Wobien Doyer Lieke de Rooij Een Latijns vierkant van orde n, is een vierkante matrix, gevuld met n verschillende symbolen waarvan elk precies
Uitwerking Puzzel 92-6 Magidoku s en verborgen symmetrieën Wobien Doyer Lieke de Rooij Een Latijns vierkant van orde n, is een vierkante matrix, gevuld met n verschillende symbolen waarvan elk precies
a a Hoe hoog is de kleinste toren op het plaatje? 97 m b d Hoe oud zijn de Martinitoren en de Eiffeltoren? De Martinitoren is meer dan
 les 14 59 Aan welke keersommen uit de tafels tot 10 denk je? b 9 70 = 630 6 80 = 480 9 7 en 6 8 a a 4 30 = 120 4 50 = 200 4 3 en 4 5 c 8 80 = 640 7 60 = 420 8 8 en 7 6 b d = 5600 = 7200 Meer antwoorden.
les 14 59 Aan welke keersommen uit de tafels tot 10 denk je? b 9 70 = 630 6 80 = 480 9 7 en 6 8 a a 4 30 = 120 4 50 = 200 4 3 en 4 5 c 8 80 = 640 7 60 = 420 8 8 en 7 6 b d = 5600 = 7200 Meer antwoorden.
Uitleg. Welkom bij de Beverwedstrijd 2006. Je krijgt 15 vragen, die je in maximaal 45 minuten moet beantwoorden.
 Uitleg Welkom bij de Beverwedstrijd 2006 Je krijgt 15 vragen, die je in maximaal 45 minuten moet beantwoorden. Je krijgt 5 vragen van niveau A, 5 vragen van niveau B en 5 vragen van niveau C. Wij denken
Uitleg Welkom bij de Beverwedstrijd 2006 Je krijgt 15 vragen, die je in maximaal 45 minuten moet beantwoorden. Je krijgt 5 vragen van niveau A, 5 vragen van niveau B en 5 vragen van niveau C. Wij denken
Antwoorden. Magische vierkanten Vierkant voor Wiskunde Doeboek 8
 Antwoorden Magische vierkanten Vierkant voor Wiskunde Doeboek 8 1 6 1 8 7 5 3 2 9 4 2 De getallen 1 tot en met 9. 3 15. 15 en 15. De som van de getallen van elke rij is 15. 4 15. De som van de getallen
Antwoorden Magische vierkanten Vierkant voor Wiskunde Doeboek 8 1 6 1 8 7 5 3 2 9 4 2 De getallen 1 tot en met 9. 3 15. 15 en 15. De som van de getallen van elke rij is 15. 4 15. De som van de getallen
2 n 1. OPGAVEN 1 Hoeveel cijfers heeft het grootste bekende Mersenne-priemgetal? Met dit getal vult men 320 krantenpagina s.
 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Figuur 124: De mayadiagrammen van enkele partities Opgaven hoofdstuk 8: Partities en andere afbeeldingen
 Hoofdstuk 16 Antwoorden of oplossingsrichtingen bij geselecteerde opgaven Opgave 8.1 a Het eerste voorbeeld van figuur 47 is het zelfde als figuur 48, dus dit hoort bij de lege partitie. Met behulp van
Hoofdstuk 16 Antwoorden of oplossingsrichtingen bij geselecteerde opgaven Opgave 8.1 a Het eerste voorbeeld van figuur 47 is het zelfde als figuur 48, dus dit hoort bij de lege partitie. Met behulp van
8. Complexiteit van algoritmen:
 8. Complexiteit van algoritmen: Voorbeeld: Een gevaarlijk spel 1 Spelboom voor het wespenspel 2 8.1 Complexiteit 4 8.2 NP-problemen 6 8.3 De oplossing 7 8.4 Een vuistregel 8 In dit hoofdstuk wordt het
8. Complexiteit van algoritmen: Voorbeeld: Een gevaarlijk spel 1 Spelboom voor het wespenspel 2 8.1 Complexiteit 4 8.2 NP-problemen 6 8.3 De oplossing 7 8.4 Een vuistregel 8 In dit hoofdstuk wordt het
44. De trapkogelbaan (AL)
 44. De trapkogelbaan (AL) Activiteit In deze activiteit onderzoekt het kind de werking van de trapkogelbaan. Dit is een type knikkerbaan waar de knikkers, door te draaien aan een hendeltje, naar boven
44. De trapkogelbaan (AL) Activiteit In deze activiteit onderzoekt het kind de werking van de trapkogelbaan. Dit is een type knikkerbaan waar de knikkers, door te draaien aan een hendeltje, naar boven
Rationale Punten op Elliptische Krommen
 Rationale Punten op Elliptische Krommen Bart Sevenster 20 juli 2011 Bachelorscriptie Begeleiding: Prof. Dr. G. van der Geer 2 P 1 Q P Q 2 1 1 2 1 P Q 2 3 KdV Instituut voor wiskunde Faculteit der Natuurwetenschappen,
Rationale Punten op Elliptische Krommen Bart Sevenster 20 juli 2011 Bachelorscriptie Begeleiding: Prof. Dr. G. van der Geer 2 P 1 Q P Q 2 1 1 2 1 P Q 2 3 KdV Instituut voor wiskunde Faculteit der Natuurwetenschappen,
Naam:... Datum:... 36 + 12 =. 2 x 15 =. 47 + 43 =. 4 x 12 =. 25 + 11 =. 6 x 7 =. 38-16 =. 100 : 4 =. 17-6 =. 36 : 6 =.
 Opvraging Wiskunde W1 36 + 12 =. 2 x 15 =. 47 + 43 =. 4 x 12 =. 25 + 11 =. 6 x 7 =. 38-16 =. 100 : 4 =. 17-6 =. 36 : 6 =. 2 Goed lezen en oplossen. Ik koop in de supermarkt een krant (80 cent), een brood
Opvraging Wiskunde W1 36 + 12 =. 2 x 15 =. 47 + 43 =. 4 x 12 =. 25 + 11 =. 6 x 7 =. 38-16 =. 100 : 4 =. 17-6 =. 36 : 6 =. 2 Goed lezen en oplossen. Ik koop in de supermarkt een krant (80 cent), een brood
Bewerkingen met krachten
 21 Bewerkingen met krachten Opgeloste Vraagstukken 2.1. Bepaal het moment van de kracht van 2N uir Fig. 2-3 rond het punt O. Laat de loodrechte OD neer vanuit O op de rechte waarlangs de kracht van 2N
21 Bewerkingen met krachten Opgeloste Vraagstukken 2.1. Bepaal het moment van de kracht van 2N uir Fig. 2-3 rond het punt O. Laat de loodrechte OD neer vanuit O op de rechte waarlangs de kracht van 2N
Getallenleer Inleiding op codeertheorie. Cursus voor de vrije ruimte
 Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
Aan de gang. Wiskunde B-dag 2015, vrijdag 13 november, 9:00u-16:00u
 Aan de gang Wiskunde B-dag 2015, vrijdag 13 november, 9:00u-16:00u Verkenning 1 (Piano) Je moet een zware piano verschuiven door een 1 meter brede gang met een rechte hoek er in. In de figuur hierboven
Aan de gang Wiskunde B-dag 2015, vrijdag 13 november, 9:00u-16:00u Verkenning 1 (Piano) Je moet een zware piano verschuiven door een 1 meter brede gang met een rechte hoek er in. In de figuur hierboven
Bijzondere kettingbreuken
 Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
Cursus KeyCreator. Tekenen van een ratel
 Cursus KeyCreator Tekenen van een ratel Maken van een ratel. Bij deze oefening gaat men gebruik maken van verschillende onderdelen van KeyCreator. Der tekening bestaat uit volgende onderdelen: Een blok
Cursus KeyCreator Tekenen van een ratel Maken van een ratel. Bij deze oefening gaat men gebruik maken van verschillende onderdelen van KeyCreator. Der tekening bestaat uit volgende onderdelen: Een blok
I.3 Functies. I.3.2 Voorbeeld. De afbeeldingen f: R R, x x 2 en g: R R, x x 2 zijn dus gelijk, ook al zijn ze gegeven door verschillende formules.
 I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
Foto s bewerken. deel 8. Roteer, verbeter, rode ogen en snij bij. ipad OMA. ipadoma.nl
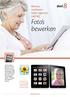 Roteer, verbeter, rode ogen en snij bij Foto s bewerken deel 8 Zonder aparte apps aan te schaffen kunt u al een aantal eenvoudige bewerkingen doen. De standaard app Foto s biedt 4 bewerkingen: Roteer,
Roteer, verbeter, rode ogen en snij bij Foto s bewerken deel 8 Zonder aparte apps aan te schaffen kunt u al een aantal eenvoudige bewerkingen doen. De standaard app Foto s biedt 4 bewerkingen: Roteer,
Rotaties in de ruimte, de ruimte van rotaties
 Rotaties in de ruimte, de ruimte van rotaties Roland van der Veen (UvA) Dit is een hands-on inleiding in de wiskunde achter rotaties. De bedoeling is om aan hand van opgaven en puzzels zelf aan de slag
Rotaties in de ruimte, de ruimte van rotaties Roland van der Veen (UvA) Dit is een hands-on inleiding in de wiskunde achter rotaties. De bedoeling is om aan hand van opgaven en puzzels zelf aan de slag
Elliptische krommen en digitale handtekeningen in Bitcoin
 Elliptische krommen en digitale handtekeningen in Bitcoin Bas Edixhoven Universiteit Leiden KNAW Bitcoin symposium Deze aantekeningen zal ik op mijn homepage plaatsen. Bas Edixhoven (Universiteit Leiden)
Elliptische krommen en digitale handtekeningen in Bitcoin Bas Edixhoven Universiteit Leiden KNAW Bitcoin symposium Deze aantekeningen zal ik op mijn homepage plaatsen. Bas Edixhoven (Universiteit Leiden)
http://www.kidzlab.nl/index2.php?option=com_content&task=vi...
 Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Apps in de wiskundeles
 Annegreet Poelman en Silke Vangheluwe Apps in de wiskundeles Nascholing over het gebruik van ipads tijdens de lessen wiskunde in het secundair onderwijs UGent - Onderwijstechnologie INLEIDING Technologie
Annegreet Poelman en Silke Vangheluwe Apps in de wiskundeles Nascholing over het gebruik van ipads tijdens de lessen wiskunde in het secundair onderwijs UGent - Onderwijstechnologie INLEIDING Technologie
Onafhankelijke verzamelingen en Gewogen Oplossingen, door Donald E. Knuth, The Art of Computer Programming, Volume 4, Combinatorial Algorithms
 Onafhankelijke verzamelingen en Gewogen Oplossingen, door Donald E. Knuth, The Art of Computer Programming, Volume 4, Combinatorial Algorithms Giso Dal (0752975) Pagina s 5 7 1 Deelverzameling Representatie
Onafhankelijke verzamelingen en Gewogen Oplossingen, door Donald E. Knuth, The Art of Computer Programming, Volume 4, Combinatorial Algorithms Giso Dal (0752975) Pagina s 5 7 1 Deelverzameling Representatie
Simon de schildpad. 2012 J van Weert 1
 Programmeren met Simon Simon de schildpad 2012 J van Weert 1 Inleiding: Wat is programmeren eigenlijk? Een computer doet niets zonder een programma. Die programma s worden geschreven door mensen: programmeurs.
Programmeren met Simon Simon de schildpad 2012 J van Weert 1 Inleiding: Wat is programmeren eigenlijk? Een computer doet niets zonder een programma. Die programma s worden geschreven door mensen: programmeurs.
Projectieve Vlakken en Codes
 Projectieve Vlakken en Codes 1. De Fanocode Foutdetecterende en foutverbeterende codes. Anna en Bart doen mee aan een spelprogramma voor koppels. De ene helft van de deelnemers krijgt elk een kaart waarop
Projectieve Vlakken en Codes 1. De Fanocode Foutdetecterende en foutverbeterende codes. Anna en Bart doen mee aan een spelprogramma voor koppels. De ene helft van de deelnemers krijgt elk een kaart waarop
Geldwisselprobleem van Frobenius
 Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Lineaire Algebra C 2WF09
 Lineaire Algebra C 2WF09 College: Instructie: L. Habets HG 8.09, Tel. 4230, Email: l.c.g.j.m.habets@tue.nl H. Wilbrink HG 9.49, Tel. 2783, E-mail: h.a.wilbrink@tue.nl http://www.win.tue.nl/wsk/onderwijs/2wf09
Lineaire Algebra C 2WF09 College: Instructie: L. Habets HG 8.09, Tel. 4230, Email: l.c.g.j.m.habets@tue.nl H. Wilbrink HG 9.49, Tel. 2783, E-mail: h.a.wilbrink@tue.nl http://www.win.tue.nl/wsk/onderwijs/2wf09
Mogelijke Onderwerpen Projectwerk Bachelor 3 Wiskunde
 Mogelijke Onderwerpen Projectwerk Bachelor 3 Wiskunde E. Jespers Departement of Mathematics Vrije Universiteit Brussel 2 Voorbeelden van algebra s van kleine dimensie Een theorie steunt steeds op het goed
Mogelijke Onderwerpen Projectwerk Bachelor 3 Wiskunde E. Jespers Departement of Mathematics Vrije Universiteit Brussel 2 Voorbeelden van algebra s van kleine dimensie Een theorie steunt steeds op het goed
