Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie
|
|
|
- Erik ter Linde
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: Datum: 25 oktober 2005 Anvang: 8:45 Tijdsduur: 2 uur Opmerkingen:. Dit tentamen telt in totaal pagina s. 2. Bij de beantwoording van de vragen moet er voldoende toelichting of uitwerking worden gegeven. Alleen een uitkomst is niet voldoende.. Dit tentamen zal behoudens calamiteiten op 9 november 2005 zijn nagekeken. Op 4 november 2005 zal van uur gelegenheid tot inzage worden gegeven. 4. De normering van de vragen is als volgt: opgave a b c 2a 2b 4a 4b 5 punten
2 Opgave (a) Zij A R. Geef een wiskundige definitie van de uitdrukking inf(a). (b) Is er een verschil tussen sup(a) = max(a)? Verandert dit als A N? (c) De rij {x n } voldoet aan lim sup x n 2 en lim inf x n 2. Wat is dan bekend over lim n x n? Antwoord: (a) inf(a) voldoet aan x A : inf(a) x (inf(a) is ondergrens) en ɛ > 0 x A : inf(a) + ɛ > x (het is de kleinste ondergrens). Voor ieder x A geldt x sup(a). Verder bestaat voor ieder ɛ > 0 een ɛ zó dat x ɛ + ɛ > sup(a). (b) Zij A = {x < } dan bestaat het maximum van A niet en het supremum wél (het supremum bestaat altijd). Voor A zij voor eindige verzamelingen sup(a) = max(a). Anders is sup(a) = en het maximum bestaat niet. (c) Uit de definitie volgt Onder de voorwaarden in (c) geldt dus De limiet bestaat dus en is gelijk aan 2. lim inf x n lim sup x n. lim inf x n = lim sup x n. Opgave 2 De functie f op IR is gedefinieerd door f(x, y, z) = x 2 + 2y 2 + z 2 + 2xy + 2xz. 2
3 (a) Bepaal de extrema van f en bepaal tevens de aard van de extrema via de tweede orde voorwaarden. (b) Bepaal de extrema van f en bepaal tevens de aard van de extrema met de vier stappen methode. Antwoord: (a) De partieële afgeleiden zijn f x f y f z = 2x + 2y + 2z = 4y + 2x = 6z + 2z. De gradient is de afgeleide omdat de gradient op IR continu is. De einige stationaire punt is (0, 0, 0). De Hesse matrix van f is H f = en hangt niet van (x, y, z) af. Voor de aard van het extremum berekenen we x (x, y, z) H f y z (x, y, z) 2x + 2y + 2z 2x + 4y 2x + 6z = 2x 2 + 2xy + 2xz + 2xy + 4y 2 + 2xz + 6z 2 = (x 2 + 4xy + 4y 2 ) + (x 2 + 4xz + 4z 2 ) + 2z 2 = (x + 2y) 2 + (x + 2z) 2 + 2z 2. Deze uitdrukking is positief voor x, y, z > 0 en wordt 0 voor x = y = z. H f is dus positief semi-definiet en (0, 0, 0) is een minimumlokatie. (b) Voor grote waarden van (x, y, z) geldt dat f(x, y, z) naar gaat de functie is dus coercief voor minimaliseering. Omdat f continu is heeft f een globaal
4 minimum (Corollary ). Stationaire punten kunnen zo als in (a) berekend worden. Omdat f(0, 0, 0) = 0 en bijvoorbeeld f(,, ) > 0 is het stationair punt een minimum. We hebben hetzelfde resultaat zo als onder (a) (uiteraard zonder berekening van de Hesse matrix. Opgave Bepaal de extrema van onder de nevenvoorwaarden f 0 (x, y, z) = x + 2z f (x) = x + y + z = en f 2 (x) = x 2 + y 2 + z = 2. Antwoord: () f 0 is continu en f () f2 (2) is niet leeg ((,, 0) is toegestaan punt), afgesloten (inverse van een afgesloten verzameling onder een continu afbeelding). Wij tonen aan dat f () f2 (2) begrensd is. Uit f = en f 2 = 2 volgt x 2 + y 2 + x y = 2 x 2 x y2 y + 4 = 2 (x 2 )2 + (y 2 )2 = 5 2 Omdat de kwadratische termen altijd positief zijn volgt hieruit ( x ) 2 5 ( en y ) Hieruit volgt, bijvoorbeeld, dat 5 x, y 5 en uit x + y + z = volgt dat z ook begrensd is. Omdat f () f2 (2) begrensd is, bestaan er dus extrema (Weierstrass). (2) De Lagrange-functie wordt en L(x, y,, zλ) = λ 0 (x + 2z) + λ (x + y + z ) + λ 2 (x 2 + y 2 + z 2) x L(x, y, z, λ) = λ 0 + λ + 2λ 2 x y L(x, y, z, λ) = λ + 2λ 2 y z L(x, y, z, λ) = 2λ 0 + λ + λ 2 4
5 2) (a) Stel λ 0 = 0, dan volgt uit L x = 0 en λ 0 : 2λ 2 x = 2λ 2 y = λ 2 x = y = 2 en met f volgt z = 0. Maar f (/2, /2, 0) = / (b) Zij λ 0 =, dan Invullen na λ 2 oplossen geeft + λ + 2λ 2 x = 0 λ + 2λ 2 y = λ + λ 2 = 0 λ = λ λ 2 + 2λ 2 x = 0 + (2x )λ 2 = 0 2 λ 2 + 2λ 2 y = (2y )λ 2 = 0 λ 2 = 2x en λ 2 = 2 2y. Uit volgt 2x = 2 2y y = 2x 2. Uit de nevenvoorwaarden volgt x 2 x + y 2 y = en invullen van de uitdrukking voor y geeft ( x 2 x + 2x ) 2 2x = x 2 x + 4x 2 2x + 4 2x + 2 = 5x 2 5x = 4 5
6 oftewel x 2 x + 4 = ( x ) 2 = = 0 x = 2 + x 2 = De bijbehorende waarde voor y, y 2 en z, z 2 zijn Dus y = z = 0 f 0 (x, y, z ) = y 2 = f 0 (x 2, y 2, z 2 ) = z 2 = 0. Het punt (x, y, z ) is een minimumlokatie een het punt (x 2, y 2, z 2 ) is een maximumlokatie. Opgave 4 Gegeven zij de functie f 0 (x, y) = x 2 y 4 (a) Onderzoek f 0 op S = {(x, y) : x > 0, y > 0} op convexiteit resp. concaviteit. (b) Bepaal de maximale waarde van f 0 (x, y) onder de nevenvoorwaarden x + y 4 en y 2 0. en Uitwerking Deel (a): Er geldt: ( Hf = 4 x 2 y 4 8 x 2 y 4 8 x 2 y 4 x 2 y x Hfx = 6 x 2 y 9 8 < 0. ) 6
7 Dus Hf is negatief semi-definiet en het volgt met Theorem 9 (d) dat f concaaf is. Uitwerking Deel (b): Uit deel (a) weten wij dat f concaaf is. Wij bestuderen het volgende probleem: onder f 0 (x, y) = x 2 y 4 min f (x, y) = x + y = 4 en f 2 (x, y) = y 2 = 0. Het probleem is convex. 2) (0, 0) is een Slaterpunt. ) De Lagrange-functie wordt met L(x, y, λ) = x 2 y 4 + λ (x + y 4) + λ 2 (y 2 ) L x (x, y, λ) = 2 x 2 y 4 + λ L y (x, y, λ) = 4 x 2 y 4 + λ + 2λ 2 y. Case I: f = 0 en f 2 < 0 (λ 0 en λ 2 = 0). 0 = 2 x 2 y 4 + λ 0 = 4 x 2 y 4 + λ 0 = x + y 4. Hieruit volgt 2 x 2 y 4 = 4 x 2 y 4 en dat geeft 2y = x. Dus y = 4/ en x = 8/. Check geeft λ > 0. Het punt (8/, 4/) is het globaal minimum van de hulpfunctie f 0. De functie f 0 heeft dus een globaal maximum bij (8/, 4/). Let op: bij f = 0 en f 2 = 0 vindt men de oplossing x = en y = maar hiervoor geldt λ < 0 en dat is geen toegestaan oplossing. Opgave 5 Bepaal met behulp van Karush-Kuhn-Tucker methode de minimale waarde van f 0 (x, y) = (x 2) 4 + (y ) 7
8 onder de nevenvoorwaarden x + y en y 2 0. Het mag hierbij veronderstelt worden dat het probleem convex is. Antwoord: ) Het probleem is convex. 2) (0, 0) is een Slaterpunt. ) De Lagrangefunctie wordt met L(x, y, λ) = (x 2) 4 + (y ) + λ (x + y ) + λ 2 (y 2 ) Case I: f < 0 en f 2 = 0. L x (x, y, λ) = 4(x 2) + λ L y (x, y, λ) = (y ) 2 + λ + 2λ 2 y. 0 = 4(x 2) 0 = (y ) 2 + 2λ 2 y 0 = y 2. Dus y = ± en x = 2. Zij y = dan volgt λ 2 = 0. Omdat f (2, ) = 0 (en wij verondersteld hebben dat f < 0) is dit geen toegestaan oplossing. Zij y = dan volgt λ 2 = 6 en f (2, ) < 0. De lokatie van het globaal minimum van f 0 is dus (2, ) en f 0 (2, ) = 8. In het oorspronkelijke probleem is (2, ) die locatie van het globaal maximum. Let op: f < 0 en f 2 < 0 geeft y = ± en x = 2. Maar f (2, ) = 0 en f 2 (2, ) = 0 en dit is tegenspraak met de veronderstelling dat f, f 2 < 0. 8
Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie
 Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: 64200 Datum:
Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: 64200 Datum:
Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie
 Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: 64200 Datum:
Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: 64200 Datum:
Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie
 Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: 611010 Datum:
Vrije Universiteit Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Convexe Analyse en Optimalisering Opleiding: Bacheloropleiding Econometrie Vakcode: 611010 Datum:
Afdeling Kwantitatieve Economie
 Afdeling Kwantitatieve Economie Wiskunde AEO V Uitwerking tentamen 1 november 2005 1. De tekenschema s in opgave 1a 1e zijn de voortekens van vermenigvuldigers en de laatste leidende hoofdminoren in een
Afdeling Kwantitatieve Economie Wiskunde AEO V Uitwerking tentamen 1 november 2005 1. De tekenschema s in opgave 1a 1e zijn de voortekens van vermenigvuldigers en de laatste leidende hoofdminoren in een
(b) Formuleer het verband tussen f en U(P, f), en tussen f en L(P, f). Bewijs de eerste. (c) Geef de definitie van Riemann integreerbaarheid van f.
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 2 juli 2015, 08:30 11:30 (12:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek Analysis
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 2 juli 2015, 08:30 11:30 (12:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek Analysis
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam and Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Boek: Optimization: Insights and Applications,
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam and Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Boek: Optimization: Insights and Applications,
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Literatuur Optimization: Insights and Applications,
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Literatuur Optimization: Insights and Applications,
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Literatuur Calculus, a complete course, Robert
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Literatuur Calculus, a complete course, Robert
4.1 College Week 4. Probleem (P 3.1 ) Zij f : D IR, met D IR n :
 4.1 College Week 4 Probleem (P 3.1 ) Zij f : D IR, met D IR n : f 0 (x) extr, f i (x) = 0, 1 i m, noemen wij een n-dimensionaal optimaliseringsprobleem met nevenvoorwaarden in vorm van een stelsel bestaande
4.1 College Week 4 Probleem (P 3.1 ) Zij f : D IR, met D IR n : f 0 (x) extr, f i (x) = 0, 1 i m, noemen wij een n-dimensionaal optimaliseringsprobleem met nevenvoorwaarden in vorm van een stelsel bestaande
Oefenexamen Wiskunde Semester
 Oefenexamen Wiskunde Semester 1 2017-2018 De cursusdienst van de faculteit Toegepaste Economische Wetenschappen aan de Universiteit Antwerpen. Op het Weduc forum vind je een groot aanbod van samenvattingen,
Oefenexamen Wiskunde Semester 1 2017-2018 De cursusdienst van de faculteit Toegepaste Economische Wetenschappen aan de Universiteit Antwerpen. Op het Weduc forum vind je een groot aanbod van samenvattingen,
III.3 Supremum en infimum
 III.3 Supremum en infimum Zowel de reële getallen als de rationale getallen vormen geordende lichamen. Deze geordende lichamen zijn echter principieel verschillend. De verzameling R is bijvoorbeeld aanzienlijk
III.3 Supremum en infimum Zowel de reële getallen als de rationale getallen vormen geordende lichamen. Deze geordende lichamen zijn echter principieel verschillend. De verzameling R is bijvoorbeeld aanzienlijk
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 26 augustus 2010, , Examenzaal
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 26 augustus 2010, 14.00 17.00, Examenzaal Het gebruik van een rekenmachine en/of telefoon is niet toegestaan. U mag geen gebruik maken van het boek
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 26 augustus 2010, 14.00 17.00, Examenzaal Het gebruik van een rekenmachine en/of telefoon is niet toegestaan. U mag geen gebruik maken van het boek
Tentamen: Kwantitatieve methoden 1.2(wiskundige methoden) Opleiding: Bacheloropleiding Economie Vakcode: 60121110
 Vrije Universiteit Amsterdam Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Kwantitatieve methoden.2(wiskundige methoden) Opleiding: Bacheloropleiding Economie
Vrije Universiteit Amsterdam Faculteit der Economische Wetenschappen en Bedrijfskunde Afdeling Econometrie Tentamen: Kwantitatieve methoden.2(wiskundige methoden) Opleiding: Bacheloropleiding Economie
Opgaven Functies en Reeksen. E.P. van den Ban
 Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam and Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott.htm Overzicht Boek: Optimization: Insights and Applications,
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam and Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott.htm Overzicht Boek: Optimization: Insights and Applications,
(10 pnt) Bepaal alle punten waar deze functie een relatief extreem of een zadelpunt heeft. Opgave 3. Zij D het gebied gegeven door
 Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
Technische Universiteit Delft Tentamen Calculus TI1106M - Uitwerkingen. 2. Geef berekeningen en beargumenteer je antwoorden.
 Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Literatuur Calculus, a complete course, Robert
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott Overzicht Literatuur Calculus, a complete course, Robert
Z.O.Z. Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 16 juni 2016, 12:30 15:30 (16:30)
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 16 juni 016, 1:30 15:30 (16:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van aantekeningen
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 16 juni 016, 1:30 15:30 (16:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van aantekeningen
Tussentoets Analyse 1
 Tussentoets Analyse Maandag 0 oktober 008, 0.00 -.00u Schrijf op ieder vel je naam en studentnummer, de naam van de docent S. Hille, O. van Gaans en je studierichting. Geef niet alleen antwoorden, leg
Tussentoets Analyse Maandag 0 oktober 008, 0.00 -.00u Schrijf op ieder vel je naam en studentnummer, de naam van de docent S. Hille, O. van Gaans en je studierichting. Geef niet alleen antwoorden, leg
Convexe Analyse en Optimalisering
 Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott college conopt docent week 6 6 De Lagrange Methode 6.1 Interpretatie
Convexe Analyse en Optimalisering Bernd Heidergott Vrije Universiteit Amsterdam en Tinbergen Institute WEB: http://staff.feweb.vu.nl/bheidergott college conopt docent week 6 6 De Lagrange Methode 6.1 Interpretatie
EERSTE DEELTENTAMEN ANALYSE C
 EERSTE DEELTENTAMEN ANALYSE C 0 november 990 9.30.30 uur Zet uw naam op elk blad dat u inlevert en uw naam en adres op de enveloppe. De verschillende onderdelen van de vraagstukken zijn zoveel als mogelijk
EERSTE DEELTENTAMEN ANALYSE C 0 november 990 9.30.30 uur Zet uw naam op elk blad dat u inlevert en uw naam en adres op de enveloppe. De verschillende onderdelen van de vraagstukken zijn zoveel als mogelijk
x a k of.x 1 a 1 / 2 + ::+.x n a n / 2 k 2 bol om a, straal k
 Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Oplossingen Oefeningen Bewijzen en Redeneren
 Oplossingen Oefeningen Bewijzen en Redeneren Goeroen Maaruf 20 augustus 202 Hoofdstuk 3: Relaties. Oefening 3..2 (a) Persoon p is grootouder van persoon q. (b) (p, q) O o O r P : [ (p, r) O (r, q) O ]
Oplossingen Oefeningen Bewijzen en Redeneren Goeroen Maaruf 20 augustus 202 Hoofdstuk 3: Relaties. Oefening 3..2 (a) Persoon p is grootouder van persoon q. (b) (p, q) O o O r P : [ (p, r) O (r, q) O ]
Examenvragen Hogere Wiskunde I
 1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
Wiskunde AEO V. Afdeling Kwantitatieve Economie. Uitwerking tentamen 6 januari 2010
 Afeling Kwantitatieve Economie Wiskune AEO V Uitwerking tentamen 6 januari 00 Een stelling ( punten) Laat c een ifferentieerbare kromme zijn, ie op een niveauverzameling van een ifferentieerbare functie
Afeling Kwantitatieve Economie Wiskune AEO V Uitwerking tentamen 6 januari 00 Een stelling ( punten) Laat c een ifferentieerbare kromme zijn, ie op een niveauverzameling van een ifferentieerbare functie
1. (a) Gegeven z = 2 2i, w = 1 i 3. Bereken z w. (b) Bepaal alle complexe getallen z die voldoen aan z 3 8i = 0.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Wiskundige Technieken 1 Uitwerkingen Tentamen 4 november 2013
 Wiskundige Technieken Uitwerkingen Tentamen 4 november 0 Normering voor 4 pt vragen andere vragen naar rato): 4pt pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
Wiskundige Technieken Uitwerkingen Tentamen 4 november 0 Normering voor 4 pt vragen andere vragen naar rato): 4pt pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
n=0 en ( f(y n ) ) ) n=0 equivalente rijen zijn.
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 8 juli 2011, 14.00 17.00 Het gebruik van een rekenmachine en/of telefoon is niet toegestaan. U mag geen gebruik maken van het boek Analysis I. Geef
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 8 juli 2011, 14.00 17.00 Het gebruik van een rekenmachine en/of telefoon is niet toegestaan. U mag geen gebruik maken van het boek Analysis I. Geef
Hints en uitwerkingen huiswerk 2013 Analyse 1 H18
 Hints en uitwerkingen huiswerk 2013 Analyse 1 H18 Rocco van Vreumingen 29 augustus 2014 1 Inhoudsopgave 1 Hints 1 3 2 Hints 2 4 3 Hints 3 5 4 Hints 4 5 5 Hints 5 6 6 Hints 6 6 7 Hints 7 6 8 Antwoorden
Hints en uitwerkingen huiswerk 2013 Analyse 1 H18 Rocco van Vreumingen 29 augustus 2014 1 Inhoudsopgave 1 Hints 1 3 2 Hints 2 4 3 Hints 3 5 4 Hints 4 5 5 Hints 5 6 6 Hints 6 6 7 Hints 7 6 8 Antwoorden
TECHNISCHE UNIVERSITEIT EINDHOVEN
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit der Wiskunde en Informatica Tentamen van Calculus voor het schakelprogramma van B (XB03) op woensdag 0 april 03, 9:00-:00 uur De uitwerkingen van de opgaven
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit der Wiskunde en Informatica Tentamen van Calculus voor het schakelprogramma van B (XB03) op woensdag 0 april 03, 9:00-:00 uur De uitwerkingen van de opgaven
Examen G0U13 Bewijzen en Redeneren Bachelor 1ste fase Wiskunde. vrijdag 31 januari 2014, 8:30 12:30. Auditorium L.00.07
 Examen G0U13 Bewijzen en Redeneren Bachelor 1ste fase Wiskunde vrijdag 31 januari 2014, 8:30 12:30 Auditorium L.00.07 Geef uw antwoorden in volledige, goed lopende zinnen. Het examen bestaat uit 5 vragen.
Examen G0U13 Bewijzen en Redeneren Bachelor 1ste fase Wiskunde vrijdag 31 januari 2014, 8:30 12:30 Auditorium L.00.07 Geef uw antwoorden in volledige, goed lopende zinnen. Het examen bestaat uit 5 vragen.
Concave programmeringsproblemen
 Concave programmeringsproblemen leren omgaan met de Stelling van Karush-Kuhn-Tucker Pierre v. Mouche Juni 2007 Verbeterde versie 0.8359 (maart 2008) Inhoudsopgave 1 Inleiding 4 1.1 Maximalisatie- en minimalisatieterminologie......................
Concave programmeringsproblemen leren omgaan met de Stelling van Karush-Kuhn-Tucker Pierre v. Mouche Juni 2007 Verbeterde versie 0.8359 (maart 2008) Inhoudsopgave 1 Inleiding 4 1.1 Maximalisatie- en minimalisatieterminologie......................
b) Uit Bayes volgt, gebruik makend van onderdeel a) P (T V )P (V ) P (T ) = (0.09)(0.07)
 Uitwerkingen tentamen 6 juli 22. We stellen T de gebeurtenis test geeft positief resultaat, F de gebeurtenis, chauffeur heeft gefraudeerd, V de gebeurtenis, chauffeur heeft vergissing gemaakt C de gebeurtenis,
Uitwerkingen tentamen 6 juli 22. We stellen T de gebeurtenis test geeft positief resultaat, F de gebeurtenis, chauffeur heeft gefraudeerd, V de gebeurtenis, chauffeur heeft vergissing gemaakt C de gebeurtenis,
Machtsfuncties al dan niet samengesteld in de vorm van een polynoom- of veeltermfunctie
 Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen 0
Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen 0
Opgaven Inleiding Analyse
 Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking Tentamen Calculus, 2DM10, maandag 22 januari 2007
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
Inleiding Wiskundige Economie (Volledig tentamen incl. Deel 2) Dr. Rene van den Brink en Dr. Harold Houba
 Inleiding Wiskundige Economie (Volledig tentamen incl. Deel 2) Dr. Rene van den Brink en Dr. Harold Houba Belangrijk Deelnemers die een vrijstelling voor Deel 1 hebben, kunnen volstaan met het maken van
Inleiding Wiskundige Economie (Volledig tentamen incl. Deel 2) Dr. Rene van den Brink en Dr. Harold Houba Belangrijk Deelnemers die een vrijstelling voor Deel 1 hebben, kunnen volstaan met het maken van
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Verbanden en functies
 Verbanden en functies 0. voorkennis Stelsels vergelijkingen Je kunt een stelsel van twee lineaire vergelijkingen met twee variabelen oplossen. De oplossing van het stelsel is het snijpunt van twee lijnen.
Verbanden en functies 0. voorkennis Stelsels vergelijkingen Je kunt een stelsel van twee lineaire vergelijkingen met twee variabelen oplossen. De oplossing van het stelsel is het snijpunt van twee lijnen.
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie
 FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Analyse A, deeltentamen Uitwerkingen maandag 1 november 2010, 9 11 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Analyse A, deeltentamen Uitwerkingen maandag 1 november 2010, 9 11 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan
V.2 Limieten van functies
 V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
Eigenschappen van de gradiënt
 Eigenschappen van de gradiënt De functie f stijgt in (a, b) het snelst in de richting van f(a, b) en daalt het snelst in tegenovergestelde richting. April 19, 2007 6 Eigenschappen van de gradiënt De functie
Eigenschappen van de gradiënt De functie f stijgt in (a, b) het snelst in de richting van f(a, b) en daalt het snelst in tegenovergestelde richting. April 19, 2007 6 Eigenschappen van de gradiënt De functie
Week 2_2. 1.2 Limieten 1.4 Continuïteit 2.2 De afgeleide 2.3 Differentiatieregels
 Week 2_2 1.2 Limieten 1.4 Continuïteit 2.2 De afgeleide 2.3 Differentiatieregels 2 Basiswiskunde_Week_2_2.nb 1.2 Voorbeeld Beschouw de uitdrukking x2 +3 x in de buurt van x = 2. x-4 Als x op 2 lijkt, dan
Week 2_2 1.2 Limieten 1.4 Continuïteit 2.2 De afgeleide 2.3 Differentiatieregels 2 Basiswiskunde_Week_2_2.nb 1.2 Voorbeeld Beschouw de uitdrukking x2 +3 x in de buurt van x = 2. x-4 Als x op 2 lijkt, dan
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
Tentamen lineaire algebra voor BWI maandag 15 december 2008, uur.
 Vrije Universiteit Amsterdam Faculteit der Exacte Wetenschappen Afdeling Wiskunde Tentamen lineaire algebra voor BWI maandag 5 december 8, 5.5-8. uur. ELK ANTWOORD DIENT TE WORDEN BEARGUMENTEERD. Er mogen
Vrije Universiteit Amsterdam Faculteit der Exacte Wetenschappen Afdeling Wiskunde Tentamen lineaire algebra voor BWI maandag 5 december 8, 5.5-8. uur. ELK ANTWOORD DIENT TE WORDEN BEARGUMENTEERD. Er mogen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
2E HUISWERKOPDRACHT CONTINUE WISKUNDE 2
 2E HUISWERKOPDRACHT CONTINUE WISKUNDE 2 Inleverdatum 30 maart 207, uiterlijk :5 uur Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je mag de theorie gebruiken die op het college
2E HUISWERKOPDRACHT CONTINUE WISKUNDE 2 Inleverdatum 30 maart 207, uiterlijk :5 uur Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je mag de theorie gebruiken die op het college
1. (a) Formuleer het Cauchy criterium voor de convergentie van een reeks
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 7 augustus 2015, 16:30 19:30 (20:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 7 augustus 2015, 16:30 19:30 (20:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek
6.0 Differentiëren Met het differentiequotiënt bereken je de gemiddelde verandering per tijdseenheid.
 6.0 Differentiëren Met het differentiequotiënt bereken je de gemiddelde verandering per tijdseenheid. f(x) = x x Differentiequotiënt van f(x) op [0, 3] = y f (3) f (0) 60 x 30 30 y x 1 Algemeen: Het differentiequotiënt
6.0 Differentiëren Met het differentiequotiënt bereken je de gemiddelde verandering per tijdseenheid. f(x) = x x Differentiequotiënt van f(x) op [0, 3] = y f (3) f (0) 60 x 30 30 y x 1 Algemeen: Het differentiequotiënt
V.4 Eigenschappen van continue functies
 V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op maandag 4 januari 2, 8.45.45 uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op maandag 4 januari 2, 8.45.45 uur. De uitwerkingen van de opgaven dienen
Inleiding Analyse 2009
 Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Je mag Zorich deel I en II gebruiken, maar geen ander hulpmiddelen (zoals andere boeken, aantekeningen, rekenmachine etc.)!
 Tentamen Analyse II. Najaar 6 (.1.7) Toelicting: Je mag Zoric deel I en II gebruiken, maar geen ander ulpmiddelen (zoals andere boeken, aantekeningen, rekenmacine etc.)! Als je bekende stellingen gebruikt
Tentamen Analyse II. Najaar 6 (.1.7) Toelicting: Je mag Zoric deel I en II gebruiken, maar geen ander ulpmiddelen (zoals andere boeken, aantekeningen, rekenmacine etc.)! Als je bekende stellingen gebruikt
3. Bepaal de convergentie-eigenschappen (absoluut convergent, voorwaardelijk convergent, divergent) van de volgende reeksen: n=1. ( 1) n (n + 1)x 2n.
 Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie
 FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Lineaire Algebra, tentamen Uitwerkingen vrijdag 4 januari 0, 9 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan. De
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Lineaire Algebra, tentamen Uitwerkingen vrijdag 4 januari 0, 9 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan. De
Vectoranalyse voor TG
 college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
Extrema van functies van meerdere variabelen
 Wiskunde voor kunstmatige intelligentie, 005 Les 3 Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde 1 de vraag behandeld hoe we minima en maxima van
Wiskunde voor kunstmatige intelligentie, 005 Les 3 Extrema van functies van meerdere variabelen Bij gewone functies van één variabel hebben we in Wiskunde 1 de vraag behandeld hoe we minima en maxima van
Uitwerking tentamen Analyse B
 Uitwerking tentamen Analyse B 30 juni 20, 7:00 20:00 uur De hieronder gegeven uitwerkingen moeten worden opgevat als voorbeelden van correcte oplossingen. In veel gevallen zijn andere correcte oplossingen
Uitwerking tentamen Analyse B 30 juni 20, 7:00 20:00 uur De hieronder gegeven uitwerkingen moeten worden opgevat als voorbeelden van correcte oplossingen. In veel gevallen zijn andere correcte oplossingen
Tentamen lineaire algebra 2 18 januari 2019, 10:00 13:00 Uitwerkingen (schets)
 Tentamen lineaire algebra 8 januari 9, : : Uitwerkingen (schets) Opgave. ( + punten) Gegeven is de matrix ( ) A =. (a) Bepaal een diagonaliseerbare matrix D en een nilpotente matrix N zodanig dat A = N
Tentamen lineaire algebra 8 januari 9, : : Uitwerkingen (schets) Opgave. ( + punten) Gegeven is de matrix ( ) A =. (a) Bepaal een diagonaliseerbare matrix D en een nilpotente matrix N zodanig dat A = N
Analyse I. 2. Formuleer en bewijs de formule van Taylor voor een functie f : R R. Stel de formules op voor de resttermen van Lagrange en Liouville.
 Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D00. Datum: Vrijdag 1 maart 003. Tijd: 14.00 17.00 uur. Plaats: VRT 03H04. Lees dit vóórdat je begint! Maak iedere ogave o een aart vel. Schrijf
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D00. Datum: Vrijdag 1 maart 003. Tijd: 14.00 17.00 uur. Plaats: VRT 03H04. Lees dit vóórdat je begint! Maak iedere ogave o een aart vel. Schrijf
Technische Universiteit Delft. ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW2030 Vrijdag 30 januari 2015,
 Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen
 Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen Maandag 4 januari 216, 1: - 13: uur 1. Beschouw voor t > de inhomogene singuliere tweede orde vergelijking, t 2 ẍ + 4tẋ + 2x = f(t, (1 waarin f
Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen Maandag 4 januari 216, 1: - 13: uur 1. Beschouw voor t > de inhomogene singuliere tweede orde vergelijking, t 2 ẍ + 4tẋ + 2x = f(t, (1 waarin f
Reeksnr.: Naam: t 2. arcsin x f(t) = 2 dx. 1 x
 Calculus, 4//4. Gegeven de reële functie ft) met als voorschrift t arcsin x ft) = dx x a) Geef het domein van de functie ft). Op dit domein, bespreek waar de functie stijgt, daalt en bepaal de lokale extrema.
Calculus, 4//4. Gegeven de reële functie ft) met als voorschrift t arcsin x ft) = dx x a) Geef het domein van de functie ft). Op dit domein, bespreek waar de functie stijgt, daalt en bepaal de lokale extrema.
Uitwerkingen tentamen Lineaire Algebra 2 16 januari, en B =
 Uitwerkingen tentamen Lineaire Algebra 2 16 januari, 215 Deze uitwerkingen zijn niet volledig, maar geven het idee van elke opgave aan. Voor een volledige oplossing moet alles ook nog duidelijk uitgewerkt
Uitwerkingen tentamen Lineaire Algebra 2 16 januari, 215 Deze uitwerkingen zijn niet volledig, maar geven het idee van elke opgave aan. Voor een volledige oplossing moet alles ook nog duidelijk uitgewerkt
Wiskunde met (bedrijfs)economische toepassingen
 FACULTEIT TEW Wiskunde met (bedrijfs)economische toepassingen Oefenexamens 1ste Bachelor TEW Eerste deel (januari) Academiejaar 2013-2014 Het examen vindt voor iedereen plaats in twee delen : het eerste
FACULTEIT TEW Wiskunde met (bedrijfs)economische toepassingen Oefenexamens 1ste Bachelor TEW Eerste deel (januari) Academiejaar 2013-2014 Het examen vindt voor iedereen plaats in twee delen : het eerste
III.2 De ordening op R en ongelijkheden
 III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Lineaire Algebra voor ST (DS6) op -4-, 4.-7. uur. Opgave Gegeven is het volgende stelsel lineaire vergelijkingen met parameters
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Lineaire Algebra voor ST (DS6) op -4-, 4.-7. uur. Opgave Gegeven is het volgende stelsel lineaire vergelijkingen met parameters
Functies van meer variabelen voor dummy s
 Functies van meer variabelen voor dummy s Dit is een 'praktische gids voor dummy s'. Hieronder kun je een aantal voorbeelden met uitleg vinden, oefeningen en uitwerkingen. De voorbeelden komen deels uit
Functies van meer variabelen voor dummy s Dit is een 'praktische gids voor dummy s'. Hieronder kun je een aantal voorbeelden met uitleg vinden, oefeningen en uitwerkingen. De voorbeelden komen deels uit
Gaap, ja, nog een keer. In één variabele hebben we deze formule nu al een paar keer gezien:
 Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Ter Leering ende Vermaeck
 Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Oefeningen Analyse I
 Oefeningen Analyse I Hoofdstuk 2: Rijen en Reeksen Inleiding Opmerking: In deze tekst kunnen fouten staan. Het zijn meestal oefeningen opgeschreven vanuit de lest, met eventueel zelf gemaakte oefeningen
Oefeningen Analyse I Hoofdstuk 2: Rijen en Reeksen Inleiding Opmerking: In deze tekst kunnen fouten staan. Het zijn meestal oefeningen opgeschreven vanuit de lest, met eventueel zelf gemaakte oefeningen
WI1708TH Analyse 3. College 5 23 februari Challenge the future
 WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
Relevante examenvragen , eerste examenperiode
 Relevante examenvragen 2007 2008, eerste examenperiode WAAR/VALS Zijn de volgende uitspraken waar of vals? Geef een korte argumentatie (bewijs) of een tegenvoorbeeld, eventueel aangevuld met een figuur.
Relevante examenvragen 2007 2008, eerste examenperiode WAAR/VALS Zijn de volgende uitspraken waar of vals? Geef een korte argumentatie (bewijs) of een tegenvoorbeeld, eventueel aangevuld met een figuur.
Functies van één veranderlijke
 Functies van één veranderlijke 952600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl /29 Elektrotechniek, Wiskunde en Informatica EWI UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde
Functies van één veranderlijke 952600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl /29 Elektrotechniek, Wiskunde en Informatica EWI UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde
Opgaven Inleiding Analyse
 Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van limiet dat lim y 0 y = 0. (b) Bewijs lim y 0 y 3 = 0 uit de definitie van limiet. (c)
Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van limiet dat lim y 0 y = 0. (b) Bewijs lim y 0 y 3 = 0 uit de definitie van limiet. (c)
WI1708TH Analyse 3. College 2 12 februari Challenge the future
 WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D2. Datum: dinsdag 29 april 28. Tijd: 14: 17:. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D2. Datum: dinsdag 29 april 28. Tijd: 14: 17:. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
Machtsfuncties al dan niet samengesteld in de vorm van een polynoom- of veeltermfunctie. 1) Met een positief exponent in de term(en) ( )
 Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen ).
Het volgende onderwerp is functie-onderzoek Dit is herhaling VWO-stof + nieuwe begrippen uit Kaper hfst 3 We bekijken de functies wiskundig en soms vanuit economisch oogpunt ( begrenzingen variabelen ).
Examen G0U13 Bewijzen en Redeneren Bachelor of Science Fysica en Wiskunde. vrijdag 3 februari 2012, 8:30 12:30
 Examen G0U13 Bewijzen en Redeneren Bachelor of Science Fysica en Wiskunde vrijdag 3 februari 2012, 8:30 12:30 Naam: Geef uw antwoorden in volledige, goed lopende zinnen. Het examen bestaat uit 5 vragen.
Examen G0U13 Bewijzen en Redeneren Bachelor of Science Fysica en Wiskunde vrijdag 3 februari 2012, 8:30 12:30 Naam: Geef uw antwoorden in volledige, goed lopende zinnen. Het examen bestaat uit 5 vragen.
Functies van één veranderlijke
 Functies van één veranderlijke 191512600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl 1/43 Elektrotechniek, Wiskunde en Informatica EWI Maxima en minima Gegeven een functie f met domein
Functies van één veranderlijke 191512600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl 1/43 Elektrotechniek, Wiskunde en Informatica EWI Maxima en minima Gegeven een functie f met domein
Inleiding Analyse. Opgaven. E.P. van den Ban. c Mathematisch Instituut Universiteit Utrecht Voorjaar 2003, herzien
 Inleiding Analyse Opgaven E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Voorjaar 2003, herzien 0 1 1 Limieten en continuïteit Opgave 1.1 (a) Bewijs direct uit de definitie van limiet dat
Inleiding Analyse Opgaven E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Voorjaar 2003, herzien 0 1 1 Limieten en continuïteit Opgave 1.1 (a) Bewijs direct uit de definitie van limiet dat
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 2 oktober 200, 3.45 6.45 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 2 oktober 200, 3.45 6.45 uur. De uitwerkingen van de opgaven
Biofysische Scheikunde: Statistische Mechanica
 Biofysische Scheikunde: Statistische Mechanica Vrije Universiteit Brussel 27 november Outline 1 Statistische Definitie van 2 Statistische Definitie van Outline 1 Statistische Definitie van 2 Statistische
Biofysische Scheikunde: Statistische Mechanica Vrije Universiteit Brussel 27 november Outline 1 Statistische Definitie van 2 Statistische Definitie van Outline 1 Statistische Definitie van 2 Statistische
8. Differentiaal- en integraalrekening
 Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Wiskunde 2 september 2008 versie 1-1 - Dit is een greep (combinatie) van 3 uit 32. De volgorde is niet van belang omdat de drie
 Wiskunde 2 september 2008 versie 1-1 - Op hoeveel verschillende manieren kun je drie zwarte pionnen verdelen over de 32 zwarte velden van een schaakbord? (Neem aan dat op elk veld hooguit één pion staat.)
Wiskunde 2 september 2008 versie 1-1 - Op hoeveel verschillende manieren kun je drie zwarte pionnen verdelen over de 32 zwarte velden van een schaakbord? (Neem aan dat op elk veld hooguit één pion staat.)
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
(x x 1 ) + y 1. x x 1 x k x x x k 1
 Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
3.2 Kritieke punten van functies van meerdere variabelen
 Wiskunde voor kunstmatige intelligentie, 007/008 Als in een kritiek punt x 0 ook de tweede afgeleide f (x 0 ) = 0 is, kunnen we nog steeds niet beslissen of de functie een minimum, maximum of een zadelpunt
Wiskunde voor kunstmatige intelligentie, 007/008 Als in een kritiek punt x 0 ook de tweede afgeleide f (x 0 ) = 0 is, kunnen we nog steeds niet beslissen of de functie een minimum, maximum of een zadelpunt
Tentamen Mathematische Statistiek (2WS05), dinsdag 3 november 2009, van uur.
 Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Tentamen Mathematische Statistiek (2WS05), dinsdag 3 november 2009, van 4.00 7.00 uur. Dit is een tentamen met gesloten boek. De uitwerkingen
Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Tentamen Mathematische Statistiek (2WS05), dinsdag 3 november 2009, van 4.00 7.00 uur. Dit is een tentamen met gesloten boek. De uitwerkingen
Uitwerkingen tentamen Lineaire Algebra 2 16 januari, en B =
 Uitwerkingen tentamen Lineaire Algebra 2 16 januari, 2015 Deze uitwerkingen zijn niet volledig, maar geven het idee van elke opgave aan Voor een volledige oplossing moet alles ook nog duidelijk uitgewerkt
Uitwerkingen tentamen Lineaire Algebra 2 16 januari, 2015 Deze uitwerkingen zijn niet volledig, maar geven het idee van elke opgave aan Voor een volledige oplossing moet alles ook nog duidelijk uitgewerkt
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Lineaire Algebra voor BMT (2DM20) op vrijdag 12 juni 2009, 9.00 Dit tentamen bestaat uit 5 open vragen, en 4 kort-antwoord vragen.
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Lineaire Algebra voor BMT (2DM20) op vrijdag 12 juni 2009, 9.00 Dit tentamen bestaat uit 5 open vragen, en 4 kort-antwoord vragen.
is de uitspraak dat als A waar is B ook waar is, A B staat voor A en B zijn equivalent: A B en B A, A staat voor de logische ontkenning van A,
 Dit college wordt gegeven aan de hand van het boek The Way of Analysis van Robert S. Strichartz (Jones and Bartlett, ISBN 0-7637-1497-6), dat ook gebruikt wordt bij het vervolgcollege in het tweede jaar
Dit college wordt gegeven aan de hand van het boek The Way of Analysis van Robert S. Strichartz (Jones and Bartlett, ISBN 0-7637-1497-6), dat ook gebruikt wordt bij het vervolgcollege in het tweede jaar
TECHNISCHE UNIVERSITEIT EINDHOVEN. Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Kansrekening (2WS2, Vrijdag 23 januari 25, om 9:-2:. Dit is een tentamen met gesloten boek. De uitwerkingen van de opgaven dienen
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Kansrekening (2WS2, Vrijdag 23 januari 25, om 9:-2:. Dit is een tentamen met gesloten boek. De uitwerkingen van de opgaven dienen
Opgave a. We berekenen eerst een normaal v van V en een normaal w van W. v = (b a) (c a) = ((2)(1) ( 2)( 2), ( 2)( 1) ( 1)(1), ( 1)( 2) (2)( 1))
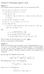 Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Lineaire algebra I (wiskundigen)
 Lineaire algebra I (wiskundigen) Voorbeelden van toetsopgaven, 011 en (1) (a) Bepaal de afstand van het punt Q = (1,, ) R 3 tot het vlak gegeven door x + y z = 1. (b) Bepaal de hoek tussen de vectoren
Lineaire algebra I (wiskundigen) Voorbeelden van toetsopgaven, 011 en (1) (a) Bepaal de afstand van het punt Q = (1,, ) R 3 tot het vlak gegeven door x + y z = 1. (b) Bepaal de hoek tussen de vectoren
2E HUISWERKOPDRACHT CONTINUE WISKUNDE
 2E HUISWERKOPDRACHT CONTINUE WISKUNDE Inleverdatum maandag 8 oktober 2017 voor het college Niet losse velletjes aan elkaar vast. Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven.
2E HUISWERKOPDRACHT CONTINUE WISKUNDE Inleverdatum maandag 8 oktober 2017 voor het college Niet losse velletjes aan elkaar vast. Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven.
