Overzicht. Inleiding. Modellering. Insertie heuristieken. Voorbeeld: CVV. Local Search. Meta heuristieken. Vehicle Routing Problem 1
|
|
|
- Evelien Baert
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Overzicht Inleiding Modellering Insertie heuristieken Voorbeeld: CVV Local Search Meta heuristieken Vehicle Routing Problem 1
2 Inleiding Gegeven Depot-knoop 0 Klant-knopen i met vraag q i, i = 1,..., n Kosten c ij tussen knoop i en knoop j, 0 i, j n Wagens k met capaciteit Q k, k = 1,... m. Gevraagd Welke routes moeten de wagens rijden, beginnend en eindigend op het depot, zodat aan de vraag van alle klanten is voldaan, terwijl de reiskosten geminimaliseerd worden. Mogelijke uitbreidingen Tijdvensters Laad, los en lunchtijden Goederen ophalen en wegbrengen (met eventuele precedentie relaties) Stochastische elementen Meerdere depots/goederen/doelstellingen Vehicle Routing Problem 2
3 Modellering I: Fisher & Jaikumar Hieronder geldt: y ik = 1 als klant i bezocht wordt door wagen k en y ik = 0 anders. Tevens geldt x ijk = 1 als klant j direct na klant i door wagen k bezocht wordt en x ijk = 0 anders. m k=1 m k=1 n i=1 n j=0 n i=0 i S j S min n n m c ij x ijk i=0 j=0 k=1 y ik = 1 1 i n y ik = m i = 0 q i y ik Q k 1 k m x ijk = y ik 0 i n, 1 k m x ijk = y jk 0 j n, 1 k m x ijk S 1 S {1,... n}, S =,1 k m Vehicle Routing Problem 3
4 Modelering II: Christofides, Mingozzi & Toth Vind alle routes r = 1,..., R voor wagen 1. V r de vracht corresponderend met r c r de kosten van route r N i de routes die klant i bevatten Nummer de routes zdd: V 1 V 2... V R. Zij r k = min {r V r Q k }. Zij r m+1 = R + 1. Stel y r = 1 als route r gebruikt wordt en y r = 0 anders. min R r=1 c r y r r N i y r = 1 1 i n r k+1 1 r=1 y r k r k r k+1, 1 k m Rr=1 y r = m Vehicle Routing Problem 4
5 Modelering III: Christofides, Mingozzi & Toth Dynamische programmerings-formulering. N = {1,2,..., n} de verzameling klanten. f(k, T ) de minimale kosten voor bedienen v.d. klanten T N door wagen 1,..., k. v(t ) de oplossing van TSP op T {0}. q(t ) = i T q i. Initialisatie: f(1, T ) = v(t ), T. Recursie voor k 2: f(k, T ) = min(f(k 1, T \S) + v(s)) S T Inperken van de zoekactie: q(t ) k 1 i=1 Q i q(s) Q k 1 m k q(n \T ) q(s) 1 k q(t ) q(n) m i=k+1 Q i q(t ) k i=1 Q i Vehicle Routing Problem 5
6 Savingsalgoritme (Clark & Wright) 1. Bereken besparingen s ij = c i0 + c 0j c ij van route 0 i j 0 t.o.v. de twee routes 0 i 0 en 0 j Orden s ij in afnemende volgorde. 3. Startend aan de top van de lijst: Parallelle versie (a) Breidt zo mogelijk een bestaande route uit, of verwerp deze tak. (b) Herhaal stap 3a voor heel de lijst. Sequentiële versie (a) Breidt zo mogelijk de huidige route uit. (b) Als de huidige route vol is, begin met de (nu) bovenste tak uit de lijst als nieuwe route. (c) Herhaal 3a en 3b tot er geen takken meer kunnen worden toegevoegd. Vehicle Routing Problem 6
7 Sweep algoritme (Gillet & Miller) Dit is een zogenaamde 2 fase methode (eerst clusteren en dan routeren). Gegeven is een Euclidisch VRP met polaire coördinaten (r i, θ i ), waarbij r i de afstand tot het depot is. Orden de klanten zodanig dat θ 1 θ 2... θ n. 1. Fase I Kies een ongebruikte wagen k. 2. Kies de onbediende klant i met de kleinste θ i. Voeg daar de klanten i + 1, i + 2,... aan toe, tot de capaciteit van wagen k bereikt is. 3. Als alle klanten zijn toegekend aan een wagen ga dan naar stap 4, herhaal anders stap Fase II Los het TSP op voor elke verzameling klanten die is toegekend aan een wagen. Vehicle Routing Problem 7
8 Christofides, Mingozzi & Toth 1. Fase IA: Sequentieel Kies kiemklant i en wagen k. 2. Bereken insertiekosten δ j = c 0j +λc ji voor alle klanten j. Voeg klanten toe in volgorde van δ j tot de route vol is. 3. Herhaal stap 1 tot dat alle klanten geclusterd zijn. 4. Fase IB: Parallel Bewaar alleen de kiemklanten. 5. Bereken insertie kosten voor de overige klanten m.b.t. alle kiemklanten. Kies de laagste insertiekosten; voeg de betreffende klant aan het bijbehorende cluster toe. 6. Herhaal stap 5 totdat er geen inserties meer mogelijk zijn. 7. Fase II: Los de TSP s op voor zowel Fase IA en IB; kies de beste. Vehicle Routing Problem 8
9 Fisher & Jaikumar 1. Fase I: Clusteren Kies voor elke wagen k een kiemklant. 2. Bereken insertiekosten δ ik voor alle klanten i m.b.t. de kiemklant van k, 1 k m. 3. Los gegeneraliseerd toewijzingsprobleem op: m k=1 n i=1 min y ik = 4. Fase II: Routeren Los TSP op voor elk cluster. m n k=1 i=0 δ ik y ik { 1, 1 i n m, i = 0 q i y ik Q k, 1 k m Vehicle Routing Problem 9
10 Collectief Vraagafhankelijk Vervoer Je huurt een zitplaats, in plaats van een hele wagen. Vertrek en bestemming zijn vrij. Er is sprake van een vooraanmeldtijd. Er zijn bepaalde spelregels per contract. Het is goedkoop vervoer. Contract Tijdvenster Maximale omrijtijd Opbrengst Combinatie-mogelijkheden Vehicle Routing Problem 10
11 Ritten en wagens Rit Gewenste tijd (vertrek- of aankomsttijd) Vertrek- en bestemmingsadres Zitplaatsen/rolstoelen In- en uitstaptijd Contract/uitzonderingen Wagen Capaciteit (zitplaatsen/rolstoelen) Werkgebied Werktijden Contracten Kosten Vehicle Routing Problem 11
12 Insertie heuristiek Gegeven: N ritten en M wagens. Zij i = Zij v = Bepaal alle toelaatbare inserties van rit i in de route van wagen v. Noteer de kosten van de goedkoopste van deze inserties als COST v. 3. Zet v v + 1. Als v M ga dan naar Wijs rit i aan wagen v toe, waarvoor geldt: COST v COST v, v. 5. Zet i i + 1. Als i N ga dan naar 1. Implementatie vraagstukken Wanneer is een insertie toelaatbaar? Wat zijn de kosten van een insertie? Hoe maak je het algoritme real-time? Vehicle Routing Problem 12
13 Notatie Tijdvensters (EPT, LPT) (EDT, LDT) DRT MRT vertrek aankomst directe rijtijd a DRT + b DRT MRT EPT LPT EDT LDT Actieve periode tijd p k + m + m n + k n q + act. per. rust actieve periode rust actieve periode Vehicle Routing Problem 13
14 Schuifvariabelen UP α = min [ min 1 j α ( ATj ET j ), WTp ] DOWN α = min [ min α j d ( LTj AT j ), WTq ] WT p wachttijd voor de actieve periode WT q d wachttijd volgend op actieve periode aantal locaties in de actieve periode Vehicle Routing Problem 14
15 Snelle test op toelaatbaarheid i + insertie? i insertie? k + m + m k rust actieve periode rust Insertie van i + : Detour = T m +,i + + T i +,m T m +,m Detour UP 2 + DOWN 3 Definitieve controle Wanneer aan de snelle test op toelaatbaarheid is voldaan, moet het volgende nog gecontroleerd worden op: Omrijtijd Capaciteit Combinaties Vehicle Routing Problem 15
16 Kosten van een insertie De kosten bestaan uit de volgende aspecten: Kosten voor de rijtijd Kosten voor de afgelegde kilometers Kosten voor de wachttijd Service kosten voor de afwijking van de gewenste tijd Service kosten voor de omrijtijd Zij W de wachttijd die voorafgaat aan de actieve periode. De kosten met betrekking op rijtijd, afstand en de service kosten m.b.t. de omrijtijd zijn vast voor elke W. De kosten voor de wachttijd is een lineaire functie in W, terwijl de (service) kosten m.b.t. de gewenste tijd kwadratisch zijn in W. Conclusie Het gebruik van actieve perioden maakt het mogelijk om een kwadratische functie in één variable te minimaliseren. Vehicle Routing Problem 16
17 Local Search 2-optimalisatie Or-optimalisatie Relocate Exchange Cross over Push route Allerlei combinaties hiervan Vehicle Routing Problem 17
18 Meta heuristieken Simulated Annealing Slechtere resultaten toestaan om te ontsnappen aan een lokaal optimum, gebaseerd op een fysisch proces. Tabu Search Met behulp van geheugen sommige iteraties verbieden om cycling te voorkomen. Genetische algoritmes Vanuit een populatie van oplossingen ontstaat een nieuwe generatie. Kinderen in deze generatie ondergaan meestal nog een mutatie. Ant systems Maakt gebruik van feromoon-sporen. Een vorm van geheugen waarbij goede oplossingen onthouden worden. Diversificatie Kleine verstoringen op het gevonden (lokale) optimum toestaan. Vehicle Routing Problem 18
INHOUDSOPGAVE 1 VOORWOORD 3 INLEIDING 4 1 BESCHRIJVING EXPERTPLANNER 5 2 LITERATUURONDERZOEK Classificatie problemen 9
 Inhoudsopgave INHOUDSOPGAVE VOORWOORD 3 INLEIDING 4 BESCHRIJVING EXPERTPLANNER 5. SAREX 6 2 LITERATUURONDERZOEK 7 2. STANDAARD VEHICLE ROUTING PROBLEM 7 2.. Classificatie problemen 9 2.2 BESTAANDE HEURISTIEKEN
Inhoudsopgave INHOUDSOPGAVE VOORWOORD 3 INLEIDING 4 BESCHRIJVING EXPERTPLANNER 5. SAREX 6 2 LITERATUURONDERZOEK 7 2. STANDAARD VEHICLE ROUTING PROBLEM 7 2.. Classificatie problemen 9 2.2 BESTAANDE HEURISTIEKEN
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2003 1 Docenten Onderdeel a Er zijn 6 vakken V 1, V 2,..., V 6. Vak V j heeft een vraag b j = 1, voor j = 1, 2,...,
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2003 1 Docenten Onderdeel a Er zijn 6 vakken V 1, V 2,..., V 6. Vak V j heeft een vraag b j = 1, voor j = 1, 2,...,
Optimalisering en Complexiteit, College 2. Han Hoogeveen, Utrecht University
 Optimalisering en Complexiteit, College 2 Han Hoogeveen, Utrecht University Inhoud vandaag Inhoud: Uitleg methode Bespreking oude opdracht: Bezorgen wenskaarten Slides staan al op het web www.cs.uu.nl/docs/vakken/opt/colleges.html
Optimalisering en Complexiteit, College 2 Han Hoogeveen, Utrecht University Inhoud vandaag Inhoud: Uitleg methode Bespreking oude opdracht: Bezorgen wenskaarten Slides staan al op het web www.cs.uu.nl/docs/vakken/opt/colleges.html
Overzicht. Inleiding. Toepassingen. Verwante problemen. Modellering. Exacte oplosmethode: B&B. Insertie heuristieken. Local Search
 Overzicht Inleiding Toepassingen Verwante problemen Modellering Exacte oplosmethode: B&B Insertie heuristieken Local Search Handelsreizigersprobleem 1 Cyclische permutatie van steden b 3 77 a 93 21 42
Overzicht Inleiding Toepassingen Verwante problemen Modellering Exacte oplosmethode: B&B Insertie heuristieken Local Search Handelsreizigersprobleem 1 Cyclische permutatie van steden b 3 77 a 93 21 42
Local search. Han Hoogeveen. 21 november, 2011
 1 Local search Han Hoogeveen 21 november, 2011 Inhoud vandaag 2 Inhoud: Uitleg methode Bespreking oude opdrachten: ˆ Bezorgen wenskaarten ˆ Roosteren tentamens Slides staan al op het web www.cs.uu.nl/docs/vakken/opt/colleges.html
1 Local search Han Hoogeveen 21 november, 2011 Inhoud vandaag 2 Inhoud: Uitleg methode Bespreking oude opdrachten: ˆ Bezorgen wenskaarten ˆ Roosteren tentamens Slides staan al op het web www.cs.uu.nl/docs/vakken/opt/colleges.html
1 Vervangingsstrategie auto
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2002 1 Vervangingsstrategie auto Onderdeel a Zij V = {0, 1, 2, 3, 4, 5, 6}, waarbij knoop i staat voor het einde
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2002 1 Vervangingsstrategie auto Onderdeel a Zij V = {0, 1, 2, 3, 4, 5, 6}, waarbij knoop i staat voor het einde
Optimalisatie van doelgroepenvervoer
 Optimalisatie van doelgroepenvervoer Richard J. Boucherie Hiska Boelema Jeroen de Cloet Léon van der Kaap Stefan Klootwijk Joram Span Bernard Hoeksma 19/09/2014 r.j.boucherie@utwente.nl / www.utwente.nl/choir
Optimalisatie van doelgroepenvervoer Richard J. Boucherie Hiska Boelema Jeroen de Cloet Léon van der Kaap Stefan Klootwijk Joram Span Bernard Hoeksma 19/09/2014 r.j.boucherie@utwente.nl / www.utwente.nl/choir
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen 08-04-2005
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Sociale Dilemma s en Speltheorie
 Sociale Dilemma s en Speltheorie Krzysztof R. Apt CWI, Amsterdam Prisoner s Dilemma C D C 2, 2 0, 3 D 3, 0 1, 1 Elke speler heeft twee strategieën: C ( cooperate ) and D ( defect ). Interpretatie: C: Je
Sociale Dilemma s en Speltheorie Krzysztof R. Apt CWI, Amsterdam Prisoner s Dilemma C D C 2, 2 0, 3 D 3, 0 1, 1 Elke speler heeft twee strategieën: C ( cooperate ) and D ( defect ). Interpretatie: C: Je
Inhoud. Introductie ORTEC TRP. Klant voorbeelden. Roadmap 3-11-2011 2
 Inhoud Introductie ORTEC TRP Klant voorbeelden Roadmap 3-11-2011 2 Introductie ORTEC TRP 3-11-2011 3 Wat is tactisch plannen? Voorbeelden Verdeling werk over medewerkers Bepaling belever-/bezoekdagen klanten
Inhoud Introductie ORTEC TRP Klant voorbeelden Roadmap 3-11-2011 2 Introductie ORTEC TRP 3-11-2011 3 Wat is tactisch plannen? Voorbeelden Verdeling werk over medewerkers Bepaling belever-/bezoekdagen klanten
Cover Page. Author: Zhiwei Yang Title: Meta-heuristics for vehicle routing and inventory routing problems Issue Date:
 Cover Page The handle http://hdl.handle.net/1887/43073 holds various files of this Leiden University dissertation Author: Zhiwei Yang Title: Meta-heuristics for vehicle routing and inventory routing problems
Cover Page The handle http://hdl.handle.net/1887/43073 holds various files of this Leiden University dissertation Author: Zhiwei Yang Title: Meta-heuristics for vehicle routing and inventory routing problems
1. Het Online platform
 www.festplanner.nl FEST is een route optimalisatie programma. Het helpt bij het weergeven van optimale routes over meerdere adressen en het neemt de planning uit handen. Inhoud 1. het Online platform...
www.festplanner.nl FEST is een route optimalisatie programma. Het helpt bij het weergeven van optimale routes over meerdere adressen en het neemt de planning uit handen. Inhoud 1. het Online platform...
Taxis Pitane Automaat. Censys BV Eindhoven
 Taxis Pitane Automaat Censys BV Eindhoven Wat is de 'automaat' van Taxis Pitane Een Taxis Pitane 'automaat' bestaat uit verschillende componenten: De belangrijkste Taxis Pitane component is wellicht het
Taxis Pitane Automaat Censys BV Eindhoven Wat is de 'automaat' van Taxis Pitane Een Taxis Pitane 'automaat' bestaat uit verschillende componenten: De belangrijkste Taxis Pitane component is wellicht het
Optimalisering en Complexiteit, College 14. Geheeltallige LPs en Planning bij Grolsch. Han Hoogeveen, Utrecht University
 Optimalisering en Complexiteit, College 14 Geheeltallige LPs en Planning bij Grolsch Han Hoogeveen, Utrecht University Branch-and-bound voor algemene ILPs (1) Neem even aan dat je een minimaliseringsprobleem
Optimalisering en Complexiteit, College 14 Geheeltallige LPs en Planning bij Grolsch Han Hoogeveen, Utrecht University Branch-and-bound voor algemene ILPs (1) Neem even aan dat je een minimaliseringsprobleem
Computationele Intelligentie
 Computationele Intelligentie Uitwerking werkcollege Representatie, Ongeïnformeerd zoeken, Heuristisch zoeken 1 lokkenwereld a. De zoekboom die door het dynamische breadth-first search algoritme wordt gegenereerd
Computationele Intelligentie Uitwerking werkcollege Representatie, Ongeïnformeerd zoeken, Heuristisch zoeken 1 lokkenwereld a. De zoekboom die door het dynamische breadth-first search algoritme wordt gegenereerd
Benaderingsalgoritmen
 Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Praktijkinstructie Externe transportplanning 3 (CLO12.3/CREBO:50196)
 instructie Externe transportplanning 3 (CLO12.3/CREBO:50196) pi.clo12.3.v2 ECABO, 1 september 2003 Alle rechten voorbehouden. Niets uit deze uitgave mag worden vermenigvuldigd, overgenomen, opgeslagen
instructie Externe transportplanning 3 (CLO12.3/CREBO:50196) pi.clo12.3.v2 ECABO, 1 september 2003 Alle rechten voorbehouden. Niets uit deze uitgave mag worden vermenigvuldigd, overgenomen, opgeslagen
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2008 2009, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Tweede bachelor Informatica Academiejaar 2008 2009, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Greedy algoritmes. Algoritmiek
 Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Netwerkstroming. Algoritmiek
 Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Transparanten bij het vak Inleiding Adaptieve Systemen: Evolutionary Computation. f(s max ) f(s) s
 Transparanten bij het vak Inleiding Adaptieve Systemen: Evolutionary Computation. M. Wiering f(s max ) f(s) s Evolutionary Computation (EC) Optimalisatie algoritmen geinspireerd door Darwin s evolutie
Transparanten bij het vak Inleiding Adaptieve Systemen: Evolutionary Computation. M. Wiering f(s max ) f(s) s Evolutionary Computation (EC) Optimalisatie algoritmen geinspireerd door Darwin s evolutie
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Twaalfde college algoritmiek. 12 mei Branch & Bound
 Twaalfde college algoritmiek 12 mei 2016 Branch & Bound 1 Branch and bound -1- Branch & bound is alleen toepasbaar op optimalisatieproblemen genereert oplossingen stap voor stap en houdt de tot dusver
Twaalfde college algoritmiek 12 mei 2016 Branch & Bound 1 Branch and bound -1- Branch & bound is alleen toepasbaar op optimalisatieproblemen genereert oplossingen stap voor stap en houdt de tot dusver
Filebestrijding middels Speltheorie
 Speltheorie p. 1/3 Filebestrijding middels Speltheorie Krzysztof R. Apt (dus niet Krzystof en zeker niet Krystof) CWI & Universiteit van Amsterdam DEPOT1 DEPOT2 Speltheorie p. 2/3 Voorbeeld 1: Kilometerheffing
Speltheorie p. 1/3 Filebestrijding middels Speltheorie Krzysztof R. Apt (dus niet Krzystof en zeker niet Krystof) CWI & Universiteit van Amsterdam DEPOT1 DEPOT2 Speltheorie p. 2/3 Voorbeeld 1: Kilometerheffing
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Verzamelingen:
Tweede bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Verzamelingen:
Examen H 111 Datum: vrijdag 9 juni 2000 Tijd: uur
 Examen H 111 Datum: vrijdag 9 juni 2000 Tijd: 10.00 13.00 uur Katholieke Universiteit Leuven Departement Burgerlijke Bouwkunde Instructies: Er zijn 5 vragen; Start de beantwoording van elk van de 5 vragen
Examen H 111 Datum: vrijdag 9 juni 2000 Tijd: 10.00 13.00 uur Katholieke Universiteit Leuven Departement Burgerlijke Bouwkunde Instructies: Er zijn 5 vragen; Start de beantwoording van elk van de 5 vragen
Optimalisatieplatform
 Personenvervoer Consultancy: analyses voor overheden en vervoerbedrijven Doelgroepenvervoer - Openbaar Vervoer Optimaliseren van bezettingsgraden en routes Anticiperen op verkeerssituatie; reistijdvoorspellingen
Personenvervoer Consultancy: analyses voor overheden en vervoerbedrijven Doelgroepenvervoer - Openbaar Vervoer Optimaliseren van bezettingsgraden en routes Anticiperen op verkeerssituatie; reistijdvoorspellingen
Heuristieken en benaderingsalgoritmen. Algoritmiek
 Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
1 In deze opgave wordt vijftien maal telkens drie beweringen gedaan waarvan er één juist is. Kruis de juiste bewering aan. (2pt. per juist antwoord).
 Tentamen Optimalisering (IN2805-I) Datum: 3 april 2008, 14.00 17.00. Docent: Dr. J.B.M. Melissen Naam: Studienummer: 1 In deze opgave wordt vijftien maal telkens drie beweringen gedaan waarvan er één juist
Tentamen Optimalisering (IN2805-I) Datum: 3 april 2008, 14.00 17.00. Docent: Dr. J.B.M. Melissen Naam: Studienummer: 1 In deze opgave wordt vijftien maal telkens drie beweringen gedaan waarvan er één juist
Tentamen Kunstmatige Intelligentie (INFOB2KI)
 Tentamen Kunstmatige Intelligentie (INFOB2KI) 30 januari 2014 10:30-12:30 Vooraf Mobiele telefoons dienen uitgeschakeld te zijn. Het tentamen bestaat uit 7 opgaven; in totaal kunnen er 100 punten behaald
Tentamen Kunstmatige Intelligentie (INFOB2KI) 30 januari 2014 10:30-12:30 Vooraf Mobiele telefoons dienen uitgeschakeld te zijn. Het tentamen bestaat uit 7 opgaven; in totaal kunnen er 100 punten behaald
Startersgids voor chauffeurs
 1 Algemeen Startersgids voor chauffeurs 1: Om de kaart in de tachograaf te steken moet men eerst op knop 1 duwen (bijrijder op knop 2) tot de lade opent. 2: Men kan nu de kaart met de chip naar boven in
1 Algemeen Startersgids voor chauffeurs 1: Om de kaart in de tachograaf te steken moet men eerst op knop 1 duwen (bijrijder op knop 2) tot de lade opent. 2: Men kan nu de kaart met de chip naar boven in
Programmeren. Inhoudsopgave
 Programmeren Inhoudsopgave Beginpunt 2 Implementatie Karhoo 3 ETA & Prijs principe 4 Implementatie prijsberekening en gegevens database 4 Het versturen, ontvangen en beantwoorden van ritaanvragen. 7 Weergeven
Programmeren Inhoudsopgave Beginpunt 2 Implementatie Karhoo 3 ETA & Prijs principe 4 Implementatie prijsberekening en gegevens database 4 Het versturen, ontvangen en beantwoorden van ritaanvragen. 7 Weergeven
Kortste Paden. Algoritmiek
 Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Optimalisatie van de logistieke processen van de bennewagens in ArcelorMittal Gent
 UNIVERSITEIT GENT FACULTEIT ECONOMIE EN BEDRIJFSKUNDE ACADEMIEJAAR 2008 2009 Optimalisatie van de logistieke processen van de bennewagens in ArcelorMittal Gent Masterproef voorgedragen tot het bekomen
UNIVERSITEIT GENT FACULTEIT ECONOMIE EN BEDRIJFSKUNDE ACADEMIEJAAR 2008 2009 Optimalisatie van de logistieke processen van de bennewagens in ArcelorMittal Gent Masterproef voorgedragen tot het bekomen
De praktijkstudie start met een korte uitleg over bestaande web- en mobiele applicaties. De stad Hasselt vormt het uitgangspunt voor de
 Woord vooraf Deze eindverhandeling vormt het sluitstuk van de gevolgde studie handelsingenieur. Bij het schrijven van deze eindverhandeling, heb ik mij kunnen verdiepen in een onderwerp dat berust op persoonlijke
Woord vooraf Deze eindverhandeling vormt het sluitstuk van de gevolgde studie handelsingenieur. Bij het schrijven van deze eindverhandeling, heb ik mij kunnen verdiepen in een onderwerp dat berust op persoonlijke
Bacheloropdracht Technische Wiskunde
 Bacheloropdracht Technische Wiskunde Optimalisatie van de planning in de thuiszorg Afspraken inplannen met behulp van Particle Swarm Optimization Marieke Dijkink Stefan Klootwijk Joram Span Begeleider:
Bacheloropdracht Technische Wiskunde Optimalisatie van de planning in de thuiszorg Afspraken inplannen met behulp van Particle Swarm Optimization Marieke Dijkink Stefan Klootwijk Joram Span Begeleider:
Vijfde college algoritmiek. 2/3 maart Exhaustive search
 Vijfde college algoritmiek 2/3 maart 2017 Exhaustive search 1 Voor- en nadelen Brute force: Voordelen: - algemeen toepasbaar - eenvoudig - levert voor een aantal belangrijke problemen (zoeken, patroonherkenning)
Vijfde college algoritmiek 2/3 maart 2017 Exhaustive search 1 Voor- en nadelen Brute force: Voordelen: - algemeen toepasbaar - eenvoudig - levert voor een aantal belangrijke problemen (zoeken, patroonherkenning)
Optimalisering en Complexiteit, College 1. Han Hoogeveen, Utrecht University
 Optimalisering en Complexiteit, College 1 Han Hoogeveen, Utrecht University Gegevens Docent : Han Hoogeveen : j.a.hoogeveen@uu.nl Vak website : http://www.cs.uu.nl/docs/vakken/opt/ Student assistenten
Optimalisering en Complexiteit, College 1 Han Hoogeveen, Utrecht University Gegevens Docent : Han Hoogeveen : j.a.hoogeveen@uu.nl Vak website : http://www.cs.uu.nl/docs/vakken/opt/ Student assistenten
Tie breaking in de simplex methode
 Tie breaking in de simplex methode Tijdens de Simplexmethode kan op een aantal momenten onduidelijk zijn wat je moet doen: 1. Variabele die de basis in gaat: Zoek de grootste coëfficiënt in de doelfunctie.
Tie breaking in de simplex methode Tijdens de Simplexmethode kan op een aantal momenten onduidelijk zijn wat je moet doen: 1. Variabele die de basis in gaat: Zoek de grootste coëfficiënt in de doelfunctie.
Optimalisatiealgoritmen voor distributieproblemen
 Vakgroep Toegepaste Wiskunde, Informatica en Statistiek Optimalisatiealgoritmen voor distributieproblemen Nathan Sinnesael Promotor: prof. dr. V. Fack Masterproef ingediend tot het behalen van de academische
Vakgroep Toegepaste Wiskunde, Informatica en Statistiek Optimalisatiealgoritmen voor distributieproblemen Nathan Sinnesael Promotor: prof. dr. V. Fack Masterproef ingediend tot het behalen van de academische
TU/e 2DD50: Wiskunde 2 (1)
 TU/e 2DD50: Wiskunde 2 () Tussentoets 26 november, tijdens de instructies Zaal: paviljoen (study hub) Time: 90min Tentamenstof: colleges 4 (LP; Simplex; dualiteit; complementaire slackness) Oude tentamens:
TU/e 2DD50: Wiskunde 2 () Tussentoets 26 november, tijdens de instructies Zaal: paviljoen (study hub) Time: 90min Tentamenstof: colleges 4 (LP; Simplex; dualiteit; complementaire slackness) Oude tentamens:
Optimaliseren in Netwerken
 Optimaliseren in Netwerken Kees Roos e-mail: C.Roos@tudelft.nl URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Optimaliseren in Netwerken Kees Roos e-mail: C.Roos@tudelft.nl URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Project Management (H 9.8 + H 22 op CD-ROM)
 Project Management (H 9.8 + H 22 op CD-ROM) CPM (Critical Path Method) Activiteiten met afhankelijkheden en vaste duur zijn gegeven. CPM bepaalt de minimale doorlooptijd van het project. PERT (Program
Project Management (H 9.8 + H 22 op CD-ROM) CPM (Critical Path Method) Activiteiten met afhankelijkheden en vaste duur zijn gegeven. CPM bepaalt de minimale doorlooptijd van het project. PERT (Program
Minimum Spanning Tree
 Minimum Spanning Tree Wat is MST? Minimum spanning tree De meest efficiënte manier vinden om een verbonden netwerk op te bouwen Wat is een tree/boom? Graaf G: een verzameling knopen (vertices): V een verzameling
Minimum Spanning Tree Wat is MST? Minimum spanning tree De meest efficiënte manier vinden om een verbonden netwerk op te bouwen Wat is een tree/boom? Graaf G: een verzameling knopen (vertices): V een verzameling
Periodieke rondritproblemen met meerdere depots
 UNIVERSITEIT GENT FACULTEIT ECONOMIE EN BEDRIJFSKUNDE ACADEMIEJAAR 2009 2010 Periodieke rondritproblemen met meerdere depots Masterproef voorgedragen tot het bekomen van de graad van Master in de Toegepaste
UNIVERSITEIT GENT FACULTEIT ECONOMIE EN BEDRIJFSKUNDE ACADEMIEJAAR 2009 2010 Periodieke rondritproblemen met meerdere depots Masterproef voorgedragen tot het bekomen van de graad van Master in de Toegepaste
Optimalisering en Complexiteit, College 10. Begrensde variabelen. Han Hoogeveen, Utrecht University
 Optimalisering en Complexiteit, College 10 Begrensde variabelen Han Hoogeveen, Utrecht University Begrensde variabelen (1) In veel toepassingen hebben variabelen zowel een ondergrens als een bovengrens:
Optimalisering en Complexiteit, College 10 Begrensde variabelen Han Hoogeveen, Utrecht University Begrensde variabelen (1) In veel toepassingen hebben variabelen zowel een ondergrens als een bovengrens:
Module 3. Maximale stromen
 Module In november 00 legde een stroomstoring een gedeelte van Europa plat. Overal moesten de kaarsen aan. oordat een gedeelte van het elektriciteitsnet uitviel, was er te weinig capaciteit om aan de vraag
Module In november 00 legde een stroomstoring een gedeelte van Europa plat. Overal moesten de kaarsen aan. oordat een gedeelte van het elektriciteitsnet uitviel, was er te weinig capaciteit om aan de vraag
Vectorruimten met inproduct
 Hoofdstuk 3 Vectorruimten met inproduct 3. Inleiding In R 2 en R 3 hebben we behalve de optelling en scalairvermenigvuldiging nog meer structuur ; bij een vector kun je spreken over zijn lengte en bij
Hoofdstuk 3 Vectorruimten met inproduct 3. Inleiding In R 2 en R 3 hebben we behalve de optelling en scalairvermenigvuldiging nog meer structuur ; bij een vector kun je spreken over zijn lengte en bij
Stochastische Modellen in Operations Management (153088)
 R1 L1 R2 S0 Stochastische Modellen in Operations Management (153088) 240 ms 10 ms Ack Internet Richard Boucherie Stochastische Operations Research TW, Ravelijn H 219 http://wwwhome.math.utwente.nl/~boucherierj/onderwijs/153088/153088.html
R1 L1 R2 S0 Stochastische Modellen in Operations Management (153088) 240 ms 10 ms Ack Internet Richard Boucherie Stochastische Operations Research TW, Ravelijn H 219 http://wwwhome.math.utwente.nl/~boucherierj/onderwijs/153088/153088.html
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
Uitwerking tentamen Algoritmiek 10 juni :00 13:00
 Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
Transport, Routing- en Schedulingproblemen. ir. H.N. Post
 Transport, Routing- en Schedulingproblemen ir. H.N. Post 1 mei 2006 Inhoudsopgave 1 Kortste pad probleem 7 1.1 Definities...................................... 7 1.2 Basisalgoritme...................................
Transport, Routing- en Schedulingproblemen ir. H.N. Post 1 mei 2006 Inhoudsopgave 1 Kortste pad probleem 7 1.1 Definities...................................... 7 1.2 Basisalgoritme...................................
Tactisch plannen Peter de Haan
 Tactisch plannen Peter de Haan Even voorstellen U Peter de Haan Universiteit Twente Toegepaste Wiskunde ORTEC Sen. Solution Architect 2 Agenda Wat is tactisch plannen Voorbeelden van tactisch plannen Hoe
Tactisch plannen Peter de Haan Even voorstellen U Peter de Haan Universiteit Twente Toegepaste Wiskunde ORTEC Sen. Solution Architect 2 Agenda Wat is tactisch plannen Voorbeelden van tactisch plannen Hoe
Figuur 1. Schematisch overzicht van de structuur van het twee-stadia recourse model.
 Samenvatting In dit proefschrift worden planningsproblemen op het gebied van routering en roostering bestudeerd met behulp van wiskundige modellen en (numerieke) optimalisatie. Kenmerkend voor de bestudeerde
Samenvatting In dit proefschrift worden planningsproblemen op het gebied van routering en roostering bestudeerd met behulp van wiskundige modellen en (numerieke) optimalisatie. Kenmerkend voor de bestudeerde
Doorzoeken van grafen. Algoritmiek
 Doorzoeken van grafen Algoritmiek Vandaag Methoden om door grafen te wandelen Depth First Search Breadth First Search Gerichte Acyclische Grafen en topologische sorteringen 2 Doolhof start eind 3 Depth
Doorzoeken van grafen Algoritmiek Vandaag Methoden om door grafen te wandelen Depth First Search Breadth First Search Gerichte Acyclische Grafen en topologische sorteringen 2 Doolhof start eind 3 Depth
Gas- en Elektrische Apparaten Service Opgericht in 1966 Klanttevredenheid v.s. Verlagen operationele kosten: Een dilemma?
 Gas- en Elektrische Apparaten Service Opgericht in 1966 Klanttevredenheid v.s. Verlagen operationele kosten: Een dilemma? John Huitink Manager IT Peter Noordanus Manager Planning Programma Geas Energiewacht
Gas- en Elektrische Apparaten Service Opgericht in 1966 Klanttevredenheid v.s. Verlagen operationele kosten: Een dilemma? John Huitink Manager IT Peter Noordanus Manager Planning Programma Geas Energiewacht
AGF Onderweg Besparingen in de routeplanning van Willem Dijk AGF B.V. Bacheloropdracht Willem Dijk AGF B.V.
 AGF Onderweg Besparingen in de routeplanning van Willem Dijk AGF B.V. Bacheloropdracht Willem Dijk AGF B.V. Auteur: Frank Gerritsen Studentnummer: s1010972 Onderwijsinstelling: Universiteit Twente Studierichting:
AGF Onderweg Besparingen in de routeplanning van Willem Dijk AGF B.V. Bacheloropdracht Willem Dijk AGF B.V. Auteur: Frank Gerritsen Studentnummer: s1010972 Onderwijsinstelling: Universiteit Twente Studierichting:
Tentamen Optimalisering (IN2520) Datum: 5 november 2004, Docent: Dr. J.B.M. Melissen
 Tentamen Optimalisering (IN2520) Datum: 5 november 2004, 14.00 17.00. Docent: Dr. J.B.M. Melissen Veel succes! 1 Deze opgave bestaat uit 15 tweekeuzevragen. Per goed antwoord krijg je 2 punten. a. Dynamisch
Tentamen Optimalisering (IN2520) Datum: 5 november 2004, 14.00 17.00. Docent: Dr. J.B.M. Melissen Veel succes! 1 Deze opgave bestaat uit 15 tweekeuzevragen. Per goed antwoord krijg je 2 punten. a. Dynamisch
Een gegeneraliseerde aanpak voor automatische foutlocalisatie. Sander Scholtus
 Een gegeneraliseerde aanpak voor automatische foutlocalisatie Sander Scholtus (s.scholtus@cbs.nl) Automatische controle en correctie Doel: geautomatiseerd verbeteren fouten in microdata Twee stappen: detecteren
Een gegeneraliseerde aanpak voor automatische foutlocalisatie Sander Scholtus (s.scholtus@cbs.nl) Automatische controle en correctie Doel: geautomatiseerd verbeteren fouten in microdata Twee stappen: detecteren
College WisCKI. Albert Visser. 16 januari, Department of Philosophy, Faculty Humanities, Utrecht University. Loodrechte Projectie
 College WisCKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 16 januari, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Zij V een deelruimte met basis v 1,..., v k.
College WisCKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 16 januari, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Zij V een deelruimte met basis v 1,..., v k.
Taxis Pitane Business Suite VERWERKING NOTEERRITTEN. Censys BV Eindhoven
 Taxis Pitane Business Suite VERWERKING NOTEERRITTEN Censys BV Eindhoven Inhoudsopgave Inleiding... 3 Karakter van een noteerrit... 4 Basis reizigers... 5 Soorten noteerritten... 6 Type noteerrit... 6 Standaard
Taxis Pitane Business Suite VERWERKING NOTEERRITTEN Censys BV Eindhoven Inhoudsopgave Inleiding... 3 Karakter van een noteerrit... 4 Basis reizigers... 5 Soorten noteerritten... 6 Type noteerrit... 6 Standaard
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 3 Leo van Iersel Technische Universiteit Delft 21 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 21 september 2016 1 / 36 LP: Lineair Programmeren min x 1 2
TW2020 Optimalisering Hoorcollege 3 Leo van Iersel Technische Universiteit Delft 21 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 21 september 2016 1 / 36 LP: Lineair Programmeren min x 1 2
Combinatoriek en rekenregels
 Combinatoriek en rekenregels Les 2: Roosters en ongeordende grepen (deze les sluit aan bij de paragrafen 3 en 4 van Hoofdstuk 1 Combinatoriek en Rekenregels van de Wageningse Methode, http://www.wageningsemethode.nl/methode/het-lesmateriaal/?s=y456v-d)
Combinatoriek en rekenregels Les 2: Roosters en ongeordende grepen (deze les sluit aan bij de paragrafen 3 en 4 van Hoofdstuk 1 Combinatoriek en Rekenregels van de Wageningse Methode, http://www.wageningsemethode.nl/methode/het-lesmateriaal/?s=y456v-d)
Datastructuren en Algoritmen III, 2010
 Datastructuren en Algoritmen III, 2010 Gunnar Brinkmann 27 september 2010 Inhoudsopgave 1 Introductie 2 2 Metaheuristieken 3 2.1 Local search............................ 5 2.1.1 Het belang van de buurfunctie..............
Datastructuren en Algoritmen III, 2010 Gunnar Brinkmann 27 september 2010 Inhoudsopgave 1 Introductie 2 2 Metaheuristieken 3 2.1 Local search............................ 5 2.1.1 Het belang van de buurfunctie..............
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
Maak Bezorging Op Dezelfde Dag Winstgevend Zodat U Kunt Concurreren Met De Besten
 Maak Bezorging Op Dezelfde Dag Winstgevend Zodat U Kunt Concurreren Met De Besten Copyright Route4Me Inc. Doen De Eisen Van Klanten Een Aanslag Op Uw Bedrijf Extreme Eisen: De eisen van klanten zijn uitgegroeid
Maak Bezorging Op Dezelfde Dag Winstgevend Zodat U Kunt Concurreren Met De Besten Copyright Route4Me Inc. Doen De Eisen Van Klanten Een Aanslag Op Uw Bedrijf Extreme Eisen: De eisen van klanten zijn uitgegroeid
Chapter 4: Continuous-time Markov Chains (Part I)
 Stochastic Operations Research I (2014/2015) Selection of exercises from book and previous exams. Chapter 4: Continuous-time Markov Chains (Part I) 1.1 Book pp 179 185 These are useful exercises to learn
Stochastic Operations Research I (2014/2015) Selection of exercises from book and previous exams. Chapter 4: Continuous-time Markov Chains (Part I) 1.1 Book pp 179 185 These are useful exercises to learn
OPERATIONS RESEARCH TECHNIEKEN L.C.M. KALLENBERG UNIVERSITEIT LEIDEN
 OPERATIONS RESEARCH TECHNIEKEN L.C.M. KALLENBERG UNIVERSITEIT LEIDEN VOORJAAR 2003 Inhoudsopgave 1 Inleiding 1 1.1 Wat is Operations Research?.............................. 1 1.2 Overzicht van de te behandelen
OPERATIONS RESEARCH TECHNIEKEN L.C.M. KALLENBERG UNIVERSITEIT LEIDEN VOORJAAR 2003 Inhoudsopgave 1 Inleiding 1 1.1 Wat is Operations Research?.............................. 1 1.2 Overzicht van de te behandelen
Hoofdstuk!7!Kortste!paden!
 oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
University of Groningen. Formulations and algorithms for rich routing problems Veenstra, Marjolein
 University of Groningen Formulations and algorithms for rich routing problems Veenstra, Marjolein IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite
University of Groningen Formulations and algorithms for rich routing problems Veenstra, Marjolein IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite
Kosten. Computationale Intelligentie. Een zoekprobleem met stapkosten. Een voorbeeld: het vinden van een route. Zoeken met kosten.
 Kosten omputationale Intelligentie Zoeken met kosten Veel zoekproblemen omvatten kosten: een afstand in kilometers; een geldbedrag; een hoeveelheid tijd;... Voorbeelden van dergelijke problemen zijn: het
Kosten omputationale Intelligentie Zoeken met kosten Veel zoekproblemen omvatten kosten: een afstand in kilometers; een geldbedrag; een hoeveelheid tijd;... Voorbeelden van dergelijke problemen zijn: het
Elfde college algoritmiek. 21 april Dijkstra en Branch & Bound
 Algoritmiek 011/11 College 11 Elfde college algoritmiek 1 april 011 Dijkstra en Branch & Bound 1 Algoritmiek 011/11 Kortste paden Gegeven een graaf G met gewichten op de takken, en een beginknoop s. We
Algoritmiek 011/11 College 11 Elfde college algoritmiek 1 april 011 Dijkstra en Branch & Bound 1 Algoritmiek 011/11 Kortste paden Gegeven een graaf G met gewichten op de takken, en een beginknoop s. We
Onderzoek naar de prijszetting van niet-dringend liggend ziekenvervoer
 Onderzoek naar de prijszetting van niet-dringend liggend ziekenvervoer 17-10-2018 1 1. Plan van Aanpak 2. AS IS 3. Respons en validiteit van het onderzoek 4. Opbouw kostenmodel 5. Analyse rit gerelateerde
Onderzoek naar de prijszetting van niet-dringend liggend ziekenvervoer 17-10-2018 1 1. Plan van Aanpak 2. AS IS 3. Respons en validiteit van het onderzoek 4. Opbouw kostenmodel 5. Analyse rit gerelateerde
Kosten. Zoekalgoritmen ( ) College 5: Zoeken met kosten. Een zoekprobleem met stapkosten. Een voorbeeld: het vinden van een route
 Kosten Zoekalgoritmen (00 00) ollege 5: Zoeken met kosten Peter de Waal, Tekst: Linda van der aag Veel zoekproblemen omvatten kosten: een afstand in kilometers; een geldbedrag; een hoeveelheid tijd; ongemak;...
Kosten Zoekalgoritmen (00 00) ollege 5: Zoeken met kosten Peter de Waal, Tekst: Linda van der aag Veel zoekproblemen omvatten kosten: een afstand in kilometers; een geldbedrag; een hoeveelheid tijd; ongemak;...
Verslimmen van event triggering
 Verslimmen van event triggering Zelflerende heuristieken Jasper Caerteling (Be-Mobile) Summit: Mobility, Safety and Smart Centres as a Service Datum: 3 november 2017 icentrale: Publiek-privaat initiatief
Verslimmen van event triggering Zelflerende heuristieken Jasper Caerteling (Be-Mobile) Summit: Mobility, Safety and Smart Centres as a Service Datum: 3 november 2017 icentrale: Publiek-privaat initiatief
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2014 2015, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2014 2015, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Tentamen combinatorische optimalisatie Tijd:
 Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
E-Global Nieuwe stadsdistributie planning 15 januari 2019 Jack Pool
 E-Global Nieuwe stadsdistributie planning 15 januari 2019 Jack Pool Districon investeert in nieuwe vormen van stadsdistributie planning Districon, jarenlange ervaring in retail, transport, ecommerce en
E-Global Nieuwe stadsdistributie planning 15 januari 2019 Jack Pool Districon investeert in nieuwe vormen van stadsdistributie planning Districon, jarenlange ervaring in retail, transport, ecommerce en
Kortste Paden. Algoritmiek
 Kortste Paden Vandaag Kortste Paden probleem All pairs / Single Source / Single Target versies DP algoritme voor All Pairs probleem (Floyd s algoritme) Dijkstra s algoritme voor Single Source Negatieve
Kortste Paden Vandaag Kortste Paden probleem All pairs / Single Source / Single Target versies DP algoritme voor All Pairs probleem (Floyd s algoritme) Dijkstra s algoritme voor Single Source Negatieve
CXEuro. De Gespecialiseerde Vrachtbeurs voor Koeriers en Expediteurs. / Een Virtuele Vloot Binnen Handbereik /
 CXEuro De Gespecialiseerde Vrachtbeurs voor Koeriers en Expediteurs k in o o Nu land! er Ned / Een Virtuele Vloot Binnen Handbereik / De oplossing voor al uw uitdagingen in de logistieke sector Koeriers:
CXEuro De Gespecialiseerde Vrachtbeurs voor Koeriers en Expediteurs k in o o Nu land! er Ned / Een Virtuele Vloot Binnen Handbereik / De oplossing voor al uw uitdagingen in de logistieke sector Koeriers:
Overzicht. 1. Definities. 2. Basisalgoritme. 3. Label setting methoden. 4. Label correcting methoden. 5. Ondergrenzen. 6.
 Overzicht 1. Definities 2. Basisalgoritme 3. Label setting methoden 4. Label correcting methoden 5. Ondergrenzen 6. Resultaten Kortste Pad Probleem 1 Definities Een graaf G = (V, E) bestaat uit een verzameling
Overzicht 1. Definities 2. Basisalgoritme 3. Label setting methoden 4. Label correcting methoden 5. Ondergrenzen 6. Resultaten Kortste Pad Probleem 1 Definities Een graaf G = (V, E) bestaat uit een verzameling
Miles handleiding. Koeriers. Android & ios.
 Miles handleiding Koeriers Android & ios www.miles.delivery Welkom bij Miles! Hoi, leuk dat je gebruik gaat maken van het meest moderne online koeriers platform van Nederland. Miles regelt koeriersopdrachten
Miles handleiding Koeriers Android & ios www.miles.delivery Welkom bij Miles! Hoi, leuk dat je gebruik gaat maken van het meest moderne online koeriers platform van Nederland. Miles regelt koeriersopdrachten
Elfde college algoritmiek. 16 mei Dijkstra, Gretige algoritmen en Branch & Bound
 Algoritmiek 013/11 College 11 Elfde college algoritmiek 1 mei 013 Dijkstra, Gretige algoritmen en Branch & Bound 1 Algoritmiek 013/11 Voorbeeld -1- A B C D E F G H 9 7 5 A B C D E F G H 0 9 9 7 5 A B C
Algoritmiek 013/11 College 11 Elfde college algoritmiek 1 mei 013 Dijkstra, Gretige algoritmen en Branch & Bound 1 Algoritmiek 013/11 Voorbeeld -1- A B C D E F G H 9 7 5 A B C D E F G H 0 9 9 7 5 A B C
Overzicht. Inleiding. Modellering. Duaal probleem. αβ-algoritme. Maximale stroom probleem. Voorbeeld. Transportprobleem 1
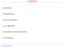 Overzicht Inleiding Modellering Duaal probleem αβ-algoritme Maximale stroom probleem Voorbeeld Transportprobleem 1 Inleiding W 1 b 1 a 1 D 1 W 2 b 2 a 2 D 2 a m Dm W n b n depots warenhuizen c ij zijn
Overzicht Inleiding Modellering Duaal probleem αβ-algoritme Maximale stroom probleem Voorbeeld Transportprobleem 1 Inleiding W 1 b 1 a 1 D 1 W 2 b 2 a 2 D 2 a m Dm W n b n depots warenhuizen c ij zijn
Tie breaking in de simplex methode
 Tie breaking in de simplex methode Tijdens de Simplexmethode kan op een aantal momenten onduidelijk zijn wat je moet doen: 1. Variabele die de basis in gaat: Zoek de grootste coëfficiënt in de doelfunctie.
Tie breaking in de simplex methode Tijdens de Simplexmethode kan op een aantal momenten onduidelijk zijn wat je moet doen: 1. Variabele die de basis in gaat: Zoek de grootste coëfficiënt in de doelfunctie.
Modeluitwerking Tentamen Computationele Intelligentie Universiteit Leiden Informatica Vrijdag 11 Januari 2013
 Modeluitwerking Tentamen Computationele Intelligentie Universiteit Leiden Informatica Vrijdag Januari 20 Opgave. Python Gegeven is de volgende (slechte) Python code:. def t(x): 2. def p(y):. return x*y
Modeluitwerking Tentamen Computationele Intelligentie Universiteit Leiden Informatica Vrijdag Januari 20 Opgave. Python Gegeven is de volgende (slechte) Python code:. def t(x): 2. def p(y):. return x*y
Computationale Intelligentie Dirk Thierens
 Computationale Intelligentie Dirk Thierens Organisatie Onderwijsvormen: Docent: Topic: Collegemateriaal: Boek: Beoordeling: hoorcollege, practicum, werkcollege Dirk Thierens Deel : Zoekalgoritmen Toets
Computationale Intelligentie Dirk Thierens Organisatie Onderwijsvormen: Docent: Topic: Collegemateriaal: Boek: Beoordeling: hoorcollege, practicum, werkcollege Dirk Thierens Deel : Zoekalgoritmen Toets
Handleiding Taxsys - Groepsvervoer
 Inleiding Taxsys Groepsvervoer: Aanmaken van routes en het beheer van routes, deelnemers gekoppeld aan instellingen en opdrachtgevers. Routes worden dynamisch opgebouwd. Mutaties op datum bepalen de samenstelling
Inleiding Taxsys Groepsvervoer: Aanmaken van routes en het beheer van routes, deelnemers gekoppeld aan instellingen en opdrachtgevers. Routes worden dynamisch opgebouwd. Mutaties op datum bepalen de samenstelling
In deze handleiding vindt u alle informatie terug die te maken heeft met gemaakte ritten. De onderstaande functies worden besproken:
 1. Ritgegevens In dit document vindt u alle opties terug die onder optie Rit details vallen in het hoofdmenu van Visego. De andere opties staan beschreven in de complete handleiding en in aparte handleidingen
1. Ritgegevens In dit document vindt u alle opties terug die onder optie Rit details vallen in het hoofdmenu van Visego. De andere opties staan beschreven in de complete handleiding en in aparte handleidingen
Computationele Intelligentie
 Computationele Intelligentie Uitwerking werkcollege Representatie, Ongeïnformeerd zoeken, Heuristisch zoeken 1 lokkenwereld a. De zoekboom die door het dynamische breadth-first search algoritme wordt gegenereerd
Computationele Intelligentie Uitwerking werkcollege Representatie, Ongeïnformeerd zoeken, Heuristisch zoeken 1 lokkenwereld a. De zoekboom die door het dynamische breadth-first search algoritme wordt gegenereerd
Algoritmiek. 8 uur college, zelfwerkzaamheid. Doel. Hoe te realiseren
 Algoritmiek Doel Gevoel en inzicht ontwikkelen voor het stapsgewijs, receptmatig oplossen van daartoe geëigende [biologische] probleemstellingen, en dat inzicht gebruiken in het vormgeven van een programmeerbare
Algoritmiek Doel Gevoel en inzicht ontwikkelen voor het stapsgewijs, receptmatig oplossen van daartoe geëigende [biologische] probleemstellingen, en dat inzicht gebruiken in het vormgeven van een programmeerbare
Elfde college algoritmiek. 29 april Algoritme van Dijkstra, Branch & Bound
 Algoritmiek 01/Algoritme van Dijkstra Elfde college algoritmiek 9 april 01 Algoritme van Dijkstra, Branch & Bound 1 Algoritmiek 01/Algoritme van Dijkstra College 10: Voorbeeld -1- A B C D E F G H 9 7 5
Algoritmiek 01/Algoritme van Dijkstra Elfde college algoritmiek 9 april 01 Algoritme van Dijkstra, Branch & Bound 1 Algoritmiek 01/Algoritme van Dijkstra College 10: Voorbeeld -1- A B C D E F G H 9 7 5
Universiteit Utrecht Faculteit Wiskunde en Informatica. Examen Optimalisering op maandag 18 april 2005, uur.
 Universiteit Utrecht Faculteit Wiskunde en Informatica Examen Optimalisering op maandag 18 april 2005, 9.00-12.00 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf
Universiteit Utrecht Faculteit Wiskunde en Informatica Examen Optimalisering op maandag 18 april 2005, 9.00-12.00 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf
Tiende college algoritmiek. 14 april Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS
 Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Infor LN Service Gebruikershandleiding Workbench Werklastverdeling
 Infor LN Service Gebruikershandleiding Workbench Werklastverdeling Publicatiegegevens Documentcode Release Aangemaakt op tsworkloaddiswbug (U9873) 10.4.x Cloud Edition (10.4.1) 18 maart 2016 Inhoudsopgave
Infor LN Service Gebruikershandleiding Workbench Werklastverdeling Publicatiegegevens Documentcode Release Aangemaakt op tsworkloaddiswbug (U9873) 10.4.x Cloud Edition (10.4.1) 18 maart 2016 Inhoudsopgave
Eindexamen wiskunde B 1-2 vwo 2002-II
 Eindexamen wiskunde B 1-2 vwo 2002-II ppervlakte Gegeven is de functie f ( x) = x 1. De lijn k raakt aan de grafiek van f in het punt (10, 3). Zie figuur 1. figuur 1 y k 1 1 f x 5p 1 Stel met behulp van
Eindexamen wiskunde B 1-2 vwo 2002-II ppervlakte Gegeven is de functie f ( x) = x 1. De lijn k raakt aan de grafiek van f in het punt (10, 3). Zie figuur 1. figuur 1 y k 1 1 f x 5p 1 Stel met behulp van
