Getaltheorie I. c = c 1 = 1 c (1)
|
|
|
- Jonathan Molenaar
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk onder de verzameling van de natuurlijke getallen te verstaan de verzameling N = {1, 2,...}, 0 wordt dan dus niet tot N gerekend. Voor de gehele getallen schrijven we: Z = {..., 2, 1, 0, 1, 2,...} 1 Priemgetallen Er zijn natuurlijke getallen die geschreven kunnen worden als product van twee of meer kleinere natuurlijke getallen, bijvoorbeeld 6 = 2 3 of 30 = 2 3 5, terwijl dit bij andere getallen, zoals 3, 13 of 29 niet mogelijk is. In het algemeen, als c = a b het product is van twee natuurlijke getallen a en b, heten a en b delers of factoren van c. Ook heet c dan een veelvoud van a (en van b). Elk natuurlijk getal heeft de volgende vanzelfsprekende ontbinding in factoren: c = c 1 = 1 c (1) Definitie 1.1 Een natuurlijk getal c > 1 dat slechts als in (1) in twee factoren ontbonden kan worden, heet een priemgetal. Elk natuurlijk getal c > 1 dat geen priemgetal is, heet een samengesteld getal. Het getal 1 is dus per definitie noch priemgetal noch samengesteld. 1.1 De zeef van Eratosthenes Om alle priemgetallen kleiner dan een gegeven getal N te bepalen, moet men uit de rij 2, 3,..., N alle samengestelde getallen verwijderen. Dit kan men systematisch doen door achtereenvolgens alle veelvouden van 2, van 3, enz. te schrappen. Hierbij kan men natuurlijk alle veelvouden van n overslaan zodra n zelf al geschrapt is (want dan zijn de veelvouden van n ook al geschrapt). Bovendien kan men bij het schrappen van de veelvouden van p beginnen bij p 2, omdat de kleinere veelvouden al eerder zijn geschrapt. De rij van getallen die niet geschrapt worden, is de rij van alle priemgetallen kleiner dan N: 2, 3, 4, 5, 6, 7, 8, 9,.... Deze methode is voor het eerst beschreven door de Griekse wiskundige Eratosthenes (±200 v. Chr.), en staat bekend als de zeef van Eratosthenes. Elke priemgetallentabel is op deze wijze gemaakt. De Griekse wiskundige Euclides (±300 v. Chr.) schreef een boek, Elementen, waarin hij op systematische wijze de gehele op dat moment bekende wiskunde behandelde. Dit boek bevat ook een gedeelte over getaltheorie. Hierin komt al de volgende stelling voor: 1
2 Stelling 1.2 Er zijn oneindig veel priemgetallen. Bewijs. Stel dat er slechts eindig veel priemgetallen waren: 2, 3, 5,..., p k. Vorm dan het product van alle priemgetallen: P = p k. Het getal P + 1 is groter dan elk van de priemgetallen, en moet dus een samengesteld getal zijn. P + 1 is echter niet deelbaar door 2, want het eerste getal na P dat door 2 deelbaar is, is P + 2. Om dezelfde reden is P + 1 niet deelbaar door 3, 5 of één van de andere priemgetallen. Tegenspraak. 1.2 De hoofdstelling van de rekenkunde Elk samengesteld getal kan geschreven worden als product van twee kleinere factoren. Als minstens één van beide samengesteld is, kan men die ook weer schrijven als product van kleinere factoren. Zo kan men doorgaan tot er slechts priemgetallen als factoren overblijven. Hieruit blijkt: elk getal groter dan 1 is een priemgetal of het product van priemgetallen. Men kan een samengesteld getal in het algemeen op verschillende manieren via een aantal tussenstappen in priemgetallen ontbinden. Iedereen weet echter dat het uiteindelijke resultaat, de ontbinding in priemfactoren, steeds hetzelfde is (afgezien van de volgorde). Deze bekende eigenschap van de natuurlijke getallen lijkt nauwelijks nadere beschouwing waard, totdat men ontdekt dat in vergelijkbare getalsystemen waarin men ook een ontbinding in priemfactoren kan definiëren de eenduidigheid van de ontbinding niet geldt. Voorbeeld: Beschouw de even getallen (2, 4, 6,...). Sommige ervan kan men schrijven als product van even factoren, bijvoorbeeld 20 = Bij andere is dit niet mogelijk. We noemen even getallen die niet het product zijn van even factoren even-priemgetallen. Dit zijn precies de even getallen die geen viervoud zijn. (Ga dit na.) Elk even getal is te schrijven als product van even-priemgetallen, maar zo n ontbinding hoeft niet eenduidig te zijn. Het getal 420 bijvoorbeeld heeft onder andere de ontbindingen 420 = 6 70 = Opgave 1.1 Bepaal alle even-priemontbindingen van 360. Opgave 1.2 Wanneer heeft een even getal een eenduidige ontbinding in evenpriemgetallen? Het feit dat de gewone ontbinding in priemfactoren wèl eenduidig is, is blijkbaar toch iets bijzonders. Het staat zelfs bekend als de hoofdstelling van de rekenkunde: Stelling 1.3 De ontbinding in priemfactoren van een natuurlijk getal is eenduidig bepaald. Bewijs. Stel dat de ontbinding niet voor alle natuurlijke getallen eenduidig is. Laat c het kleinste natuurlijke getal zijn dat op (minstens) twee verschillende manieren in priemfactoren kan worden ontbonden: c = p 1 p 2 p k = q 1 q 2 q l met p 1 p 2 p k en q 1 q 2 q k. Geen van de priemfactoren p i kan gelijk zijn aan een priemfactor q j, want dan zou men c door deze factor kunnen delen en zou er een kleiner natuurlijk getal zijn dan c met twee ontbindingen. Dit zou in tegenspraak zijn met de keuze van c. Men kan nu veronderstellen p 1 < q 1. Dan geldt 2
3 p 1 q 1 < q 1 q 1 q 1 q 2 q 1 q 2 q l = c. Het getal c = c p 1 q 1 = q 1 (q 2 q 3 q l p 1 ) heeft volgens de aannames een eenduidige priemontbinding. p 1 is een priemfactor van c en van p 1 q 1, dus ook van c. p 1 is echter geen factor van q 2 q 3 q l, dus ook niet van q 2 q 3 q l p 1. Tegenspraak. Opgave 1.3 Waarom is het bovenstaande bewijs niet overdraagbaar op het geval van de even-priemgetallen? Opgave 1.4 Gegeven is een positief geheel getal n, n > 2. V n is de verzameling getallen van de vorm kn + 1, waarin k een positief geheel getal is. Een getal m V n heet onontbindbaar in V n als er geen getallen p, q V n bestaan met m = pq. Bewijs dat er een getal in V n bestaat dat op meer dan één manier te schrijven is als het product van in V n onontbindbare elementen. (Schrijfwijzen die slechts in de volgorde van de factoren verschillen worden als gelijk beschouwd.) (IWO 1977) 2 Ggd s en kgv s Gegeven zijn twee natuurlijke getallen a en b. Het grootste natuurlijke getal dat zowel een deler is van a als van b heet de grootste gemene deler van a en b. Notatie: ggd(a, b) of kortweg (a, b). Het kleinste getal dat zowel een veelvoud van a als van b is, heet het kleinste gemene veelvoud van a en b. Notatie: (a, b) of kortweg [a, b]. a is een deler van b korten we af tot a b. Bewijs met behulp van de hoofdstelling van de rekenkunde: Opgave 2.1 Elke gemeenschappelijke deler van a en b is ook een deler van ggd(a, b). Opgave 2.2 Elk gemeenschappelijk veelvoud van a en b is ook een veelvoud van (a, b). Opgave 2.3 ggd(a, b) (a, b) = a b. Opgave 2.4 Als d = ggd(a, b) dan geldt ggd( a d, b d ) = 1. Stelling 2.1 Bij elk tweetal natuurlijke getallen a en b bestaan er gehele getallen q (voor quotiënt) en r (voor rest) zo, dat b = qa + r en 0 r < a. Bewijs. Noem het kleinste veelvoud van a dat groter is dan b (q + 1)a, en noem r = b qa. q en r voldoen dan aan de gevraagde eigenschappen. Men kan de ggd van twee getallen bepalen door beide in priemfactoren te ontbinden. Vooral bij grote getallen kan dit echter een omvangrijk werk zijn. Er is een veel snellere methode. Deze berust op het volgende feit: als b = qa + r, q Z, dan geldt ggd(a, b) = ggd(a, r). Elke deler van a en b is immers ook een deler van r = b qa en omgekeerd is elke deler van a en r een deler van b = qa + r. Om de ggd(a, b) te 3
4 bepalen kan men daarom het volgende algoritme gebruiken: b = q 1 a + r 1 (0 r 1 < a) a = q 2 r 1 + r 2 (0 r 2 < r 1 ) r 1 = q 3 r 2 + r 3 (0 r 3 < r 2 ) r 2 = q 4 r 3 + r 4 (0 r 4 < r 3 ).. r k 2 = q k r k 1 + r k (0 r k < r k 1 ) r k 1 = q k+1 r k + r k+1 (r k+1 = 0) We weten zeker dat er een k N is waarvoor r k+1 = 0, want anders zou de rij a, b, r 1, r 2,... een oneindige, strikt dalende rij natuurlijke getallen zijn, en zo n rij bestaat niet. (Bewijs dit.) Hieruit blijkt vervolgens dat r k = ggd(r k, r k 1 ) = ggd(r k 1, r k 2 ) = = ggd(r 1, a) = ggd(a, b). Een voorbeeld: bepaal ggd(1970, 1066) = = = = = = = = = = = De ggd van deze twee getallen is dus 2. Het bovenstaande algoritme voor het berekenen van ggd s staat al beschreven in Euclides Elementen en heet daarom het algoritme van Euclides. Opgave 2.5 Bepaal ggd(30444, 11868), ggd(16913, 16949) en ggd(9597, 4841). Opgave 2.6 Bewijs: als ggd(a, b) = 1, dan ggd(a + b, a b) {1, 2}. Opgave 2.7 Bewijs: als ggd(a, b) = 1, dan ggd(a + b, a 2 ab + b 2 ) {1, 3}. Opgave 2.8 Bewijs de volgende varianten van stelling 2.1: (1) als a en b gehele getallen zijn en a 0, bestaan er gehele getallen q en r met 0 r < a en b = qa + r. (2) als a en b gehele getallen zijn en a 0, bestaan er gehele getallen q en r met 1 2 a < r 1 2 a en b = qa + r. Opgave 2.9 Op variant (2) uit de vorige opgave kan men een algoritme baseren analoog aan het algoritme van Euclides. Omdat de hierbij optredende resten in het algemeen kleiner zijn dan bij Euclides algoritme, werkt dit algoritme meestal sneller. Ga dit na voor de ggd s uit opgave 2. Opgave 2.10 a is een natuurlijk getal met de volgende eigenschappen: (1) a 100 geeft bij deling door 73 rest 2. (2) a 101 geeft bij deling door 73 rest 69. Bepaal de rest bij deling van a door 73 Stelling 2.2 Bij elk tweetal natuurlijke getallen a en b zijn er gehele getallen m en n zo, dat ggd(a, b) = ma + nb. Bewijs. De verzameling S van alle getallen van de vorm xa + yb met x en y geheel heeft een kleinste positieve element. Stel dat dit ma + nb is. Elke deler van a en 4
5 b is ook een deler van ma + nb. In het bijzonder is dus ggd(a, b) een deler van ma + nb. Anderzijds is het voor zekere gehele q en r zo, dat a = q(ma + nb) + r met 0 r < ma + nb. Dit betekent dat r = (1 qm)a qnb, dus r behoort tot S. Maar ma + nb is het kleinste positieve element van S, dus r = 0. Bijgevolg is ma + nb een deler van a. Evenzo bewijst men dat ma + nb een deler is van b, dus ma + nb (a, b). Er was al bewezen dat ggd(a, b) een deler van ma + nb is, dus moet gelden ma + nb = ggd(a, b). Een ander bewijs van deze stelling kan men uit het algoritme van Euclides afleiden: kijk nog eens naar de algemene techniek en merk op dat ggd(a, b) = r k, dus dat uit de voorlaatste vergelijking volgt ggd(a, b) = r k 2 q k r k 1 en uit de vergelijking daarvoor ggd(a, b) = r k 2 q k (r k 3 q k 1 r k 2 ). Zo voortgaande kan men ggd(a, b) uitdrukken in r i s met steeds lagere rangnummers, en uiteindelijk in a en b. Dit geeft dus ook een methode om zulke getallen m en n daadwerkelijk te bepalen. Opgave 2.11 Bepaal getallen m en n als boven voor de getallenparen uit opgave 2. Opgave 2.12 Bepaal gehele getallen x en y zo, dat 91x + 221y = Opgave 2.13 Bewijs dat elk geheel getal n te schrijven is in de vorm n = 29x+13y waarbij x en y geheel zijn. Opgave 2.14 Bepaal het kleinste natuurlijke getal N zo, dat elk natuurlijk getal n > N geschreven kan worden als n = 29x + 13y met x en y natuurlijk. 3 Volledige Inductie Om de geldigheid te bewijzen van een uitspraak van de vorm Voor ieder natuurlijk getal n geldt P (n), waarbij P (n) staat voor een bewering (propositie) waarin n voorkomt, maakt men vaak gebruik van de volgende methode: 1. Men bewijst P (1). 2. Men bewijst dat als P (1), P (2),..., P (k) gelden, dan ook P (k + 1) geldt. Hieruit volgt de geldigheid van P (n) voor alle natuurlijke n. Immers, zou P (n) niet voor alle natuurlijke getallen n gelden, dan zou er een kleinste natuurlijke waarde n 0 zijn waarvoor P (n 0 ) niet geldt. n 0 is niet gelijk aan 1 wegens (1) en omdat P (1) tot en met P (n 0 1) wel gelden, geldt P (n 0 ) ook op grond van (2). Tegenspraak. Voorbeeld: voor elk natuurlijk getal n geldt n 2 = 1 6n(n + 1)(2n + 1). Bewijs. de geldigheid van de formule voor n = 1 is duidelijk. Stel dat de formule ook voor alle n k geldt. Dan volgt: k 2 +(k+1) 2 = ( k 2 )+ (k+1) 2 = 1 6 k(k+1)(2k+1)+(k+1)2 = 1 6 (k+1)(2k2 +7k+6) = 1 6 (k+1)(k+2)(2k+3) en dit is precies de formule voor n = k
6 Opgave 3.1 Bewijs de volgende beweringen met volledige inductie voor alle natuurlijke n: (1) (2n 1) = n 2 ; (2) n = 1 2n(n + 1); (3) n 3 = ( n) 2 ; (4) a n b n is deelbaar door a b; (5) 3 3n n 1 is deelbaar door 11. Opmerking: in plaats van f(1) + f(2) + + f(n) gebruikt men vaak de korte notatie n i=1 f(i). Zo kan men bijvoorbeeld de derde formule uit de vorige opgave schrijven als n i=1 i3 = ( n k=1 k) 2. 4 Gemengde opgaven Opgave 4.1 Bewijs dat men uit elke verzameling van 52 gehele getallen er twee kan kiezen waarvan de som of het verschil een veelvoud is van 100. Opgave 4.2 Er zijn paren priemgetallen die verschil twee hebben, zoals (5, 7) en (29, 31). Bestaan er ook priemgetallen p 1, p 2, p 3 zo, dat p 3 p 2 = p 2 p 1 = 2? Opgave 4.3 p 1 en p 2 zijn priemgetallen groter dan 3 met verschil 2. Bewijs dat p 1 + p 2 deelbaar is door 12. Opgave 4.4 Bewijs dat voor elk natuurlijk getal n, 9 n + 63 deelbaar is door 72. Opgave 4.5 Bewijs dat n 3 + n2 2 + n3 6 voor alle natuurlijke n een natuurlijk getal is. Opgave 4.6 Bepaal vier verschillende paren natuurlijke getallen zo, dat het verschil van hun kwadraten gelijk is aan 105. Opgave 4.7 Bewijs dat geen priemgetal is en geef minstens drie priemfactoren ervan. Opgave 4.8 Bewijs dat er precies één derdemacht van de vorm 2p + 1 is, waarin p priem is. Opgave 4.9 Bewijs dat ggd(n 3 + 2n, n 4 + 3n 2 + 1) = 1 voor elke n N. Opgave 4.10 Bewijs dat 3n 2 1 voor geen enkel natuurlijk getal n een kwadraat is. Opgave 4.11 Bepaal gehele x en y zo, dat 101x + 753y = Opgave 4.12 n wordt in het tientallig stelsel geschreven met 300 enen en een aantal nullen. Is n een kwadraat? 6
7 Lesbrief 2 Getaltheorie II 1 Lineaire vergelijkingen Een vergelijking van de vorm ax + by = c, a, b, c Z (1) heet een lineaire vergelijking. In de getaltheorie gaat het er slechts om gehele oplossingen te vinden, d.w.z. gehele getallen x en y die aan de vergelijking voldoen. Hierbij kunnen a en b beide niet-negatief worden verondersteld. (Substitueer anders x = x of y = y.) Als a = 0 of b = 0 is het onderzoek van (1) geen probleem. Stel daarom ax + by = c, a, b, c Z, a, b > 0. (2) Als d een gemeenschappelijke deler van a en b is, volgt uit (2) dat d ook een deler van c moet zijn. Stelling 1.1 (2) heeft geen gehele oplossingen als c geen veelvoud van ggd(a, b) is. In de eerste lesbrief over getaltheorie is al bewezen dat er gehele getallen m en n zijn zo, dat am + bn = ggd(a, b). Als dus c = k ggd(a, b) voor een zekere gehele k, dan is (x = km, y = kn) een oplossing van (2). Zijn er nog meer oplossingen? Stel dat (x 1, y 1 ) en (x 2, y 2 ) beide oplossingen zijn. Substitueer deze oplossingen in (2) en trek de vergelijkingen van elkaar af, dan ontstaat met de notatie u = x 1 x 2, v = y 1 y 2 de vergelijking au + bv = 0. (3) Deel deze vergelijking door ggd(a, b) en schrijf a = a ggd(a,b), b = b ggd(a,b), dan krijgen we: a u + b v = 0, ggd(a, b ) = 1. (4) Het getal A = a u = b v is een gemeenschappelijk veelvoud van a en b. Het is dus ook een veelvoud van (a, b ). We weten dat (a, b ) ggd(a, b ) = a b. Omdat ggd(a, b ) = 1 is het dus voor zekere gehele r waar dat A = ra b. Hieruit volgt: u = rb, v = ra. (5) Omgekeerd voldoet ook ieder paar (u, v) van de vorm (5) voor elke gehele r aan (4), dus ook aan (3), zodat (5) alle gehele oplossingen van (3) beschrijft. Stelling 1.2 De collectie van alle paren (u, v) van de vorm u = rb ggd(a, b), v = ra ggd(a, b), r Z is gelijk aan de collectie van alle gehele oplossingen van (3). 1
8 Het gevolg hiervan is: Stelling 1.3 Vergelijking (2) heeft slechts gehele oplossingen indien voor zekere gehele k geldt dat c = kggd(a, b). Als in dat geval (x 0, y 0 ) een gehele oplossing is, wordt de collectie van alle gehele oplossingen gegeven door: x = x 0 + rb ggd(a, b), y = y 0 + ra ggd(a, b), r Z. Opgave 1.1 Bepaal alle gehele oplossingen (indien aanwezig) van: (a) 3x 2y = 0 (e) 6x + 3y = 1 (b) 3x 2y = 2 (f) 23x + 59y = 2 (c) 6x 2y = 2 (g) 9x 51y = 7 (d) 4x + 3y = 1 (h) 14x 63y = 91 2 Congruenties en restklassen Definitie 2.1 Stel a, b, m Z, m > 1. Indien a en b bij deling door m dezelfde rest geven, d.w.z. indien a b = cm voor zekere c Z, heten a en b congruent modulo m. Notatie: a b mod m. Voorbeelden: 29 9 mod 10, 3 63 mod 5, 7 1 mod 8, mod 13. Stelling 2.2 Als a b mod m en b c mod m dan is a c mod m. Stelling 2.3 Als a b mod m en c d mod m dan is a + c b + d mod m. Stelling 2.4 Als a b mod m dan is voor elke gehele c ook ac bc mod m. Gevolg: als a b mod m en c d mod m dan is ac bd mod m. Opgave 2.1 Bewijs de vorige drie stellingen. Rekenen met congruenties lijkt dus erg op het rekenen met vergelijkingen. Er is echter een belangrijk verschil: uit ac bc mod m met c 0 mod m hoeft niet te volgen dat a b mod m. Voorbeeld: mod 10, maar 12 7 mod 10. In andere gevallen gaat het wel: mod 5 en 12 7 mod 5. Stelling 2.5 Als ac bc mod m en ggd(c, m) = 1, dan is a b mod m. Bewijs. ac bc mod m betekent dat voor zekere gehele k geldt (a b)c = km. Aangezien ggd(c, m) = 1 moet elke priemfactor van c in k bevat zijn, d.w.z. k = lc voor zekere gehele l, dus (a b)c = lcm. Omdat ggd(c, m) = 1 geldt zeker c 0 mod m (want ggd(0, m) = m voor alle gehele m), dus deze vergelijking kan door c gedeeld worden. 2
9 Rekent men modulo m, dan zijn er m verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door m. De verzameling van alle gehele getallen die éénzelfde rest geven heet een restklasse modulo m. Er zijn dus precies m verschillende restklassen modulo m. De restklasse die een getal a bevat, noteert men als a. Deze notatie is natuurlijk niet eenduidig bepaald, want als a b mod m, stellen a en b dezelfde restklasse modulo m voor en omgekeerd. Zo is bijvoorbeeld 8 gelijk aan 13 modulo 7. De keuze van precies één getal uit elk van de m restklassen modulo m geeft wat men noemt een volledig stel resten modulo m. 0, 1, 2, 3, 4 is bijvoorbeeld een volledig stel resten modulo 5, maar 11, 5, 9, 18, 3 ook. Opgave 2.2 Ga na of de volgende congruenties juist zijn: mod 11, mod 13, mod 8, mod 4. Opgave 2.3 Bewijs dat n 2 0 mod 4 of n 2 1 mod 4 voor alle gehele n. Opgave 2.4 Welke resten kan n 3 geven bij deling door 9 als n geheel is? Opgave 2.5 Bepaal de rest bij deling van 2 35 door 63, door 80 en 2 35 door 127. Opgave 2.6 Bepaal het kleinste getal n N zo, dat 2 46 n mod 47. Opgave 2.7 S(n) is de som van de cijfers van n in het tientallig stelsel. Bewijs dat S(n) n mod 9 en S(n) n mod 3. Opgave 2.8 Voor welke natuurlijke n geldt n = 144 S(n)? Opgave 2.9 Bewijs het volgende criterium voor deelbaarheid door 11: stel n = a 1 a 2 a k waarin a 1,..., a k de cijfers van n in het tientallig stelsel zijn. n is een elfvoud dan en slechts dan als de alternerende som a 1 a 2 + a 3 a 4 + ± a k een elfvoud is. Opgave 2.10 Bewijs: als ggd(m, n) = 1, a b mod m en a b mod n dan a b mod mn. (Omgekeerd geldt natuurlijk dat als a b mod mn dan a b mod m en a b mod n, ook als ggd(m, n) 1.) Opgave 2.11 Laat zien dat 0, 3 0, 3 1, 3 2,..., 3 15 een volledig stel resten modulo 17 vormen. Geldt dit ook voor 0, 2 0, 2 1, 2 2,..., 2 15? Opgave 2.12 Bewijs: als ggd(a, m) = 1 en a b mod m dan geldt ook ggd(b, m) = 1. Opgave 2.13 Op welke cijfers eindigen de getallen 6 811, en 3 999? Opgave 2.14 Bepaal de resten bij deling van door 3, 5, 11 en 13. Opgave 2.15 Bewijs dat voor alle oneven natuurlijke getallen m en k de som 1 k + 2 k + + (m 1) k deelbaar is door m. 3
10 3 De kleine stelling van Fermat De volgende stelling kan het rekenen modulo een priemgetal sterk vereenvoudigen. Stelling 3.1 (P. de Fermat, ) Als p een priemgetal is, en a is een geheel getal zo, dat ggd(a, p) = 1, dan geldt a p 1 1 mod p. Voorbeelden: mod 11, mod 37. Bewijs. Beschouw a, 2a,..., (p 1)a. Geen tweetal van deze getallen zit in dezelfde restklasse modulo p. Stel namelijk ia ja mod p met 1 j < i p 1, dan volgt op grond van stelling (2.5) dat i j mod p, een tegenspraak. Geen van de getallen a, 2a,..., (p 1)a zit in de restklasse 0, want geen van die getallen is een p-voud. Deze restklassen zijn dus precies de restklassen 1, 2,..., (p 1), eventueel in een andere volgorde. Uit het gevolg van stelling (2.4) volgt nu a 2a (p 1)a 1 2 (p 1) mod p. Omdat p een priemgetal is, mag op grond van stelling (2.5) deze congruentie worden gedeeld door 1 2 (p 1). Er staat dan a p 1 1 mod p. Opgave 3.1 p is een priemgetal. Bewijs dat n p n mod p voor alle gehele n. Opgave 3.2 Geldt mod 341? Opgave 3.3 Bepaal de kleinste n N zo, dat n mod 37, n 7 74 mod 37, n 7 12 mod Opgave 3.4 Bewijs dat 2730 een deler is van n 13 n voor alle gehele n. Opgave 3.5 Bewijs dat deelbaar is door 7. 4 De stelling van Euler Het bovenstaande bewijs van de kleine stelling van Fermat berust op twee feiten: 1. de restklassen van a, 2a,..., (p 1)a zijn allemaal verschillend (en dus de restklassen van 1, 2,..., (p 1) in zekere volgorde). 2. uit de congruentie a 2a (p 1)a 1 2 (p 1) mod p mogen we de factoren 1, 2,..., (p 1) wegdelen. Kan men dezelfde methode gebruiken bij het rekenen modulo m als m geen priemgetal is? Stel a is een natuurlijk getal met ggd(a, m) = 1. Beschouw a, 2a,..., (m 1)a. In verband met (2) en ook wegens stelling (2.5) schrappen we uit deze rij de veelvouden ka van a met ggd(k, m) 1. Er blijft een deelrij r 1 a, r 2 a,..., r k a = (m 1)a over. Als r i a en r j a (i j) in dezelfde restklasse zitten, dan geldt r i a r j a mod m en omdat ggd(a, m) = 1 impliceert dit r i r j mod m. 0 < r i en r j < m maken deze laatste congruentie echter onmogelijk. Alle r i a zitten dus in verschillende restklassen. Hetzelfde geldt natuurlijk ook voor de getallen r i zelf. Deze getallen zijn 4
11 de natuurlijke getallen kleiner dan m die met m onderling ondeelbaar zijn (d.w.z. ggd(r i, m) = 1). Er geldt echter ook voor alle i dat ggd(r i a, m) = 1. Stel immers r i a = qm + t met 0 t < m. Dan is ggd(m, t) = 1, want elke gemeenschappelijke priemfactor van m en t is ook een factor van r i a, dus van r i of van a. Maar ggd(r i, m) = 1 en ggd(a, m) = 1. Tegenspraak. De conclusie is dat de restklassen r 1, r 2,..., r k dezelfde zijn als r 1 a, r 2 a,..., r k a, eventueel in een andere volgorde. Gevolg: r 1 a r 2 a r k a r 1 r 2 r k mod m en omdat ggd(r i, m) = 1 voor alle i volgt hieruit a k 1 mod m. Het getal k, het aantal natuurlijke getallen kleiner dan m dat met m onderling ondeelbaar is, noteert men als ϕ(m). De functie ϕ heet de ϕ-functie van Euler, naar Leonhard Euler( ). We hebben nu bewezen: Stelling 4.1 Als ggd(a, m) = 1, dan geldt a ϕ(m) 1 mod m. Voor de ϕ-functie kunnen we een expliciete uitdrukking afleiden. Dit doen we met twee hulpstellingen. Stelling 4.2 Als p een priemgetal is, dan geldt voor ieder natuurlijk getal n dat ϕ(p n ) = p n 1 (p 1). Bewijs. Alleen de veelvouden van p zijn niet onderling ondeelbaar met p n. Daarvan zijn er p n 1 kleiner dan of gelijk aan p n, dus volgt ϕ(p n ) = p n p n 1. Stelling 4.3 Als ggd(m, n) = 1 dan geldt ϕ(mn) = ϕ(m)ϕ(n). Bewijs. Beschouw de mn getallen van de vorm xm + yn (0 x < n, 0 y < m). Deze zitten allemaal in verschillende restklassen modulo mn. Stel namelijk dat x 1 m + y 1 n x 2 m + y 2 n mod mn, dan geldt voor zekere gehele k dat (x 1 x 2 )m + (y 1 y 2 )n = kmn. Omdat ggd(m, n) = 1 is x 1 x 2 dan een veelvoud van n en y 1 y 2 een veelvoud van m, tegenspraak. Omdat ggd(m, n) = 1 geldt ggd(xm + yn, mn) = 1 dan en slechts dan als ggd(xm + yn, m) = 1 en ggd(xm + yn, n) = 1. Maar ggd(xm + yn, m) = ggd(yn, m) = ggd(y, m) omdat ggd(m, n) = 1 en evenzo ggd(xm + yn, n) = ggd(x, n). Het is duidelijk dat ggd(a, mn) = ggd(a + kmn, mn) voor alle gehele k. In plaats van het aantal getallen kleiner dan mn te tellen die met mn onderling ondeelbaar zijn, kan men dus net zo goed het aantal van deze getallen tellen in een willekeurig volledig stel resten modulo mn. Het stelsel {xm + yn} als boven is precies zo n volledig stel resten, en bewezen is dat ggd(xm + yn, mn) = 1 dan en slechts dan als ggd(x, n) = 1 en ggd(y, m) = 1. Hieruit volgt dat ϕ(mn) = ϕ(m)ϕ(n). Combinatie van de vorige twee stellingen levert waarin p 1, p 2,..., p r verschillende priemgetal- Stelling 4.4 Als m = p k1 1 pk2 2 pkr r len zijn, dan geldt ϕ(m) = m (p 1 1)(p 2 1) (p r 1) p 1 p 2 p r 5
12 Voorbeeld: m = 300 = , dus ϕ(300) = = 80. Bijgevolg is het voor iedere gehele a met ggd(a, 300) = 1 waar dat a 80 1 mod 300. Opgave 4.1 Bepaal ϕ(360). Opgave 4.2 Voor welke natuurlijke n geldt ϕ(n) = 2 7 n? Opgave 4.3 Bepaal de laatste twee cijfers van het getal Opgave 4.4 Bewijs dat er in de rij (2 k 3) k N oneindig veel getallen voorkomen die allemaal onderling ondeelbaar zijn. (IWO 1971) Opgave 4.5 m en n zijn verschillende positieve gehele getallen zo, dat de laatste drie cijfers van 1978 m en 1978 n overeenstemmen. Bepaal de minimale waarde van m + n. (IWO 1978) 5 Gemengde opgaven Opgave 5.1 n is een geheel getal groter dan 1. Bewijs dat n geen priemgetal is. Opgave 5.2 p n is het n-de priemgetal als we de priemgetallen van klein naar groot rangschikken. Bewijs dat p n < 2 2n. Opgave 5.3 Bewijs dat het getal 2 2n + 1 voor elke gehele n > 1 eindigt op een 7. Opgave 5.4 Bepaal a en b zo, dat a + b = 5432 en (a, b) = Opgave 5.5 Bepaal de laatste twee cijfers van Opgave 5.6 Bewijs dat voor elke natuurlijke n geldt dat 3 6n 2 6n mod 35. Opgave 5.7 Bepaal alle natuurlijke getallen die gelijk zijn aan het kwadraat van de som van hun cijfers. Opgave 5.8 Bewijs dat 2 4n voor geen enkel positief geheel getal n een priemgetal is. Opgave 5.9 Bewijs dat de som van de cijfers van elk veelvoud van 99 minstens 18 is. Opgave 5.10 Bewijs dat er geen derdemacht van de vorm 2 n + 1 bestaat. Opgave 5.11 Stel p is een priemgetal dat bij deling door 30 rest r geeft. Bewijs dat r dan een priemgetal is of gelijk is aan 1. Geldt hetzelfde bij deling door 60? Opgave 5.12 p is een priemgetal. Bewijs dat er bij elk natuurlijk getal a kleiner dan p precies één natuurlijk getal b kleiner dan p bestaat zo, dat ab 1 mod p. Opgave 5.13 p is een priemgetal. Bewijs de stelling van Wilson: (p 1)! 1 mod p. Bewijs ook het omgekeerde: als voor een natuurlijk getal m geldt dat 6
13 (m 1)! 1 mod m, dan is m een priemgetal. Opgave 5.14 Voor welke natuurlijke getallen n geldt 5 n 4 n mod 61? 7
14 Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P (x) = a n x n + a n 1 x n a 1 x + a 0, (a n 0), heet een polynoom of veelterm in de variabele x. Het getal n heet de graad van P (x), de constante getallen a n, a n 1,..., a 0 heten de coëfficiënten. Zijn P (x) en Q(x) polynomen van graad respectievelijk m en n dan is het mogelijk P (x) door Q(x) te delen, d.w.z. men kan polynomen S(x) (quotiënt) en R(x) (rest) bepalen zo, dat P (x) = Q(x)S(x) + R(x) (1) waarbij de graad r van de rest R(x) kleiner is dan de graad m van Q(x) (als m > n voldoen S(x) 0, P (x) = R(x)). Men kan S(x) en R(x) bepalen met een staartdeling. Hebben we bijvoorbeeld P (x) = 2x 3 3x 2 + 5x + 5 en Q(x) = 3x 2 2, dan geldt 3x 2 2 / 2x 3 3x x + 5 \ 3 x 1 = S(x) 2x x 3x x 3x x + 3 = R(x) In dit geval geldt dus 2x 3 3x 2 + 5x + 5 = (3x 2 2)( 2 3 x 1) + ( 19 3 x + 3). De deling eindigt altijd zodra de graad van de rest kleiner is dan de graad van de deler Q(x). Opgave 1.1 Bepaal quotiënt en rest bij deling van (a) 5x 7 3x 6 + x 2 door 3x 4 5. (c) x 10 1 door x 1. (b) 2x 3 + 4x 2 x 3 door x 3 + x. De coëfficiënten a i zijn in het algemeen reële getallen. Soms wordt ook gewerkt met polynomen met uitsluitend gehele coëfficiënten. Het is van belang op te merken dat als P (x) en Q(x) beide gehele coëfficiënten hebben en de coëfficiënt van de hoogste macht ±1 is, het quotiënt en de rest bij deling van P (x) door Q(x) weer polynomen met gehele coëfficiënten zijn. (Ga dit na.) Beschouw weer in het algemeen vergelijking (1). Stel nu Q(x) = x p. De rest is dan een polynoom van graad nul, dus een constante: P (x) = (x p)s(x) + R. Substitueer x = p, dan volgt R = P (p). De rest bij deling van P (x) door x p is dus P (p). Als in het bijzonder P (p) = 0, dan geldt P (x) = (x p)s(x). Van P (x) kan men dus een factor x p afsplitsen. Is q p een tweede nulpunt van P (x), dan is 0 = P (q) = (q p)s(q), dus ook S(q) = 0. Van S(x) is dus een factor x q af te splitsen. Als in het algemeen p 1, p 2,..., p k verschillende nulpunten van P (x) zijn, dan geldt P (x) = (x p 1 )(x p 2 ) (x p k )P (x). We vinden dus: 1
15 Stelling 1.1 Elk polynoom van graad n, n > 0, heeft ten hoogste n nulpunten. Er zijn polynomen zonder reële nulpunten, bijvoorbeeld P (x) = x Maar elk polynoom van oneven graad heeft minstens één reëel nulpunt. Stel namelijk x 0, dan geldt P (x) = a n x n +a n 1 x n 1 + +a 0 = x n (a n + an 1 a0 x + + x ) (n oneven en n a n 0). Als x voldoende groot is, is an 1 x + + a0 x < a n n, dus als x voldoende groot positief is, heeft P (x) hetzelfde teken als a n, en als x voldoende groot negatief is, heeft P (x) juist het tegengestelde teken. Omdat polynomen continue functies zijn, moet er dan ook minstens één nulpunt zijn. Stelling (1.1) kan men vaak op de volgende wijze gebruiken: weet men dat het polynoom P (x) van graad kleiner dan of gelijk aan n is en meer dan n nulpunten heeft, dan moet het van graad nul zijn. Maar een constante functie met een nulpunt moet identiek nul zijn, dus P (x) 0. Alle coëfficiënten zijn dan ook nul. Voorbeeld: Stel dat P (x) = a 2 x 2 + a 1 x + a 0 voldoet aan P (x) 1 voor alle x [ 1, 1]. Dan geldt a 2 2. Bewijs.Stel a 2 > 2. Noem Q(x) = 2x 2 1. Dan Q(±1) = 1, Q(0) = 1. Noem P (x) = 2 a 2 P (x) dan geldt P (x) < P (x) 1 op [ 1, 1]. Nu is R(x) = Q(x) P (x) een eerstegraads polynoom met R( 1) > 0, R(0) < 0 en R(1) > 0. R heeft dus minstens twee nulpunten, dus R is identiek nul, m.a.w. Q(x) P (x), in tegenspraak met P (x) < 1 op [ 1, 1]. De veronderstelling a 2 > 2 was dus onjuist Figuur 1: de grafiek van Q(x). Voorbeeld: Elk polynoom van positieve graad met gehele coëfficiënten geeft voor gehele x-waarden ook gehele functiewaarden. Kunnen die waarden allemaal priemgetallen zijn? Het antwoord is nee. Stel namelijk P (x) = a n x n + + a 0 en stel dat voor een zekere gehele k P (k) = p met p priem. Beschouw voor een gehele waarde van i P (k + ip) P (k) = a n ((k + ip) n k n ) + + a 1 ((k + ip) k). Voor iedere j is a j b j deelbaar door a b, dus P (k + ip) P (k) is deelbaar door k + ip k = ip. Voor elke gehele i is P (k + ip) dus deelbaar door p. Zouden al deze waarden priemgetallen zijn, dan zouden ze allemaal gelijk zijn aan p. Het polynoom P (x) p zou dan oneindig veel verschillende nulpunten hebben. Tegenspraak. Er is al aangetoond dat van P (x) een factor x a kan worden afgesplitst zodra P (a) = 0: P (x) = (x a)s(x). Geldt ook S(a) = 0, dan kan ook van S(x) een factor x a worden afgesplitst: P (x) = (x a) 2 T (x). Kan men zo doorgaande k maal een factor x a afsplitsen (P (x) = (x a) k U(x)) en geldt U(a) 0 (zodat er niet nog meer factoren x a afgesplitst kunnen worden) dan heet a een k-voudig nulpunt van P (x). Het getal k heet de multipliciteit van het nulpunt a. Een k- voudig nulpunt kan men opvatten als k samenvallende nulpunten. Stelling (1.1) is blijkbaar uit te breiden: Stelling 1.2 Het aantal nulpunten, elk geteld met zijn multipliciteit, van een polynoom van graad n > 0 bedraagt ten hoogste n. 2
16 Uit de regels voor differentiëren volgt: Stelling 1.3 Als a een k-voudig nulpunt van P (x) is (k > 1), dan is a een (k 1)- voudig nulpunt van P (x). Als a een enkelvoudig nulpunt van P (x) is, dan geldt P (a) 0. Stel dat het polynoom P (x) = a n x n + + a 0 (a n 0) precies n (niet noodzakelijk verschillende) nulpunten x 1, x 2,..., x n heeft. Dan is Q(x) = a n (x x 1 )(x x 2 ) (x x n ) een polynoom van dezelfde graad met ook x 1, x 2,..., x n als nulpunten. Het verschil is van graad kleiner dan n, heeft minstens n nulpunten, en is dus identiek nul. Na uitwerken van de haakjes in de uitdrukking voor Q(x) moet daarom de coëfficiënt van elke macht x k gelijk zijn aan a k. In het bijzonder is de constante term a 0 = ( 1) n a n x 1 x 2 x n, m.a.w. het product van alle nulpunten is ( 1) n a0 a n. Vergelijken van de coëfficiënten van x n 1 geeft a n 1 = a n (x 1 + x x n ), m.a.w. de som van alle nulpunten is an 1 a n. Vergelijken van de coëfficiënten van de andere machten geeft nog meer betrekkingen tussen de coëfficiënten en de nulpunten, maar de twee genoemde betrekkingen zijn de belangrijkste. Opgave 1.2 Stel P (x) = a 3 x 3 + a 2 x 2 + a 1 x + a 0 voldoet aan P (x) 1 als x [ 1, 1]. Bewijs a 3 4. (Men kan in het algemeen bewijzen dat als een n-de graads polynoom aan deze voorwaarde voldoet, dan a n 2 n 1.) Opgave 1.3 Bewijs stelling (1.3). Opgave 1.4 a en n zijn gehele getallen. De vergelijking x 3 x 2 + ax 2 n = 0 heeft drie gehele wortels. Bepaal a en n. (NWO 1970) Opgave 1.5 P (x) = (1 3x + 3x 2 ) 84 (1 + 3x 3x 2 ) 184 wordt uitgewerkt tot P (x) = a n x n + + a 0. Bepaal de som a n + a n a 0. Opgave 1.6 P (x) = a n x n + + a 0 voldoet aan P (x) = P ( x) voor alle x. Bewijs dat a i = 0 voor alle oneven i. Bewijs ook: als P (x) = P ( x) voor alle x, dan is a i = 0 voor alle even i. Opgave 1.7 Bewijs dat als men het product (1 x + x 2 x x 100 )(1 + x + x 2 + x x 100 ) uitwerkt, een polynoom ontstaat dat slechts even machten van x bevat. Opgave 1.8 Bepaal de rest na deling van x + x 3 + x 9 + x 27 + x 81 + x 243 door (a) x 1 (b) x 2 1. Opgave 1.9 Een onbekend polynoom geeft rest 2 na deling door x 1 en rest 1 na deling door x 2. Wat is de rest na deling door (x 1)(x 2)? Opgave 1.10 Uitwerken van (x 2 x + 1) n (x 2 x + 2) n + (1 + x) n + (2 x) n, n > 2, geeft a 2n 2 x 2n a 1 x + a 0. Bewijs dat a 2n 2 + a 2n a 2 = 0. (NWO 1963) Opgave 1.11 P (x) = x 2 + ax + 1 en Q(x) = x 2 + x + a. Bepaal alle waarden van a waarvoor P en Q een gemeenschappelijk nulpunt bezitten. Opgave 1.12 Bepaal alle mogelijke polynomen van de vorm P (x) = x(x a)(x b)(x c) + 1 met a, b en c positief geheel en onderling verschillend die geschreven 3
17 kunnen worden als product van twee polynomen van positieve graad met gehele coëfficiënten. Opgave 1.13 Bewijs dat een polynoom met gehele coëfficiënten de waarde 14 voor geen enkele gehele waarde van de variabele kan aannemen als het de waarde 7 voor vier gehele waarden van de variabele aanneemt. Opgave 1.14 P (x) is een polynoom met gehele coëfficiënten en positieve graad n. Er zijn precies k gehele getallen N waarvoor P (N) 2 = 1. Bewijs dat k n 2. 2 De interpolatieformule van Lagrange Door elk tweetal punten (x 0, y 0 ), (x 1, y 1 ) met x 0 < x 1 kan men de grafiek van een eerstegraads polynoom (een rechte lijn) trekken. Dit polynoom is te schrijven als P (x) = y 0 x x 1 x 0 x 1 + y 1 x x 0 x 1 x 0. Door elk drietal punten (x 0, y 0 ), (x 1, y 1 ), (x 2, y 2 ) met x 0 < x 1 < x 2 kan men de grafiek trekken van het tweedegraads polynoom (x x 1 )(x x 2 ) P (x) = y 0 (x 0 x 1 )(x 0 x 2 ) + y (x x 0 )(x x 2 ) 1 (x 1 x 0 )(x 1 x 2 ) + y (x x 0 )(x x 1 ) 2 (x 2 x 0 )(x 2 x 1 ). In het algemeen geldt: Stelling 2.1 Stel gegeven x 0 < x 1 < < x n en n + 1 getallen y 0, y 1,..., y n, dan voldoet het polynoom P (x) = n i=0 y i (x x 0 ) (x x i 1 )(x x i+1 ) (x x n ) (x i x 0 ) (x i x i 1 )(x i x i+1 ) (x i x n ) aan P (x i ) = y i voor i = 0, 1,..., n. Het is ook het enige polynoom van graad hooguit n met deze eigenschap. Bewijs. Door invullen controleert men dat inderdaad P (x i ) = y i voor alle i. Zou een tweede polynoom Q(x) van graad hooguit n dezelfde eigenschap hebben, dan zou P (x) Q(x) nul zijn in de n + 1 punten x 0, x 1,..., x n. Dit kan alleen als het verschil identiek nul is, dus als P en Q gelijk zijn. Het bepalen van een functie die in voorgeschreven punten voorgeschreven waarden aanneemt, heet interpoleren. De interpolatieformule uit bovenstaande stelling is afkomstig van de franse wiskundige J.L. Lagrange( ). Opgave 2.1 Bepaal het polynoom P van graad hooguit 2 dat voldoet aan (a) P (0) = 1, P (1) = 0 en P (2) = 0. (b) P (0) = 0, P (1) = 1 en P (2) = 0. (c) P (0) = 0, P (1) = 0 en P (2) = 1. Opgave 2.2 Gebruik opgave (2) om een polynoom van graad hooguit 2 te vinden dat voldoet aan P (0) = π, P (1) = e en P (2) = π e. 4
18 Opgave 2.3 Noem Q(x) = (x x 0 )(x x 1 ) (x x n ) en definieer voor i = 0, 1,..., n L i (x) = Q(x) (x x i )Q (x i ) als x x i en L i (x i ) = 1. Bewijs dat P (x) uit de stelling geschreven kan worden als P (x) = n y i L i (x). i=0 3 Polynomen in meer variabelen Elke eindige som van termen van de vorm c x k1 1 xk2 2 xkn n waarin de k i nietnegatieve gehele exponenten zijn, heet een polynoom in de variabelen x 1, x 2,..., x n. De getallen c heten de coëfficiënten van het polynoom. Neem aan dat gelijksoortige termen, d.w.z. termen met hetzelfde stel exponenten k 1, k 2,..., k n zijn samengenomen. Voorbeeld voor n = 3: 2x 2 1x 2 x 5 3+5x 1 x 6 1x 2 x 3 (In de tweede term geldt k 2 = k 3 = 0.) Vult men voor n 1 van de variabelen vaste waarden in, dan ontstaat een polynoom in de overblijvende variabele. De coëfficiënten van dit polynoom zijn zelf polynomen in de n 1 andere variabelen. Als P 1 (x 1 ), P 2 (x 2 ),..., P n (x n ) polynomen in respectievelijk x 1, x 2,..., x n zijn, dan is het product P 1 (x 1 )P 2 (x 2 ) P n (x n ) een polynoom in x 1, x 2,..., x n. Een voorbeeld is (x )(x 2 5)(3x 3 3 2x x 3 5). Het is echter niet waar dat elk polynoom in n variabelen ook geschreven kan worden als product van n polynomen in één variabele. Zo is het bijvoorbeeld duidelijk dat er geen polynomen P 1 (x 1 ) en P 2 (x 2 ) bestaan met P 1 (x 1 )P 2 (x 2 ) = x x 2 2. Een polynoom in meer dan één variabele kan oneindig veel nulpunten hebben. Zo geldt bijvoorbeeld x 2 1 x 2 2 = 0 voor alle punten (x 1, x 2 ) met x 1 = ±x 2. Stelling 3.1 Als het polynoom P (x 1, x 2,..., x n ) voor alle reële waarden van x 1, x 2,..., x n de waarde 0 aanneemt, dan zijn alle coëfficiënten van het polynoom nul. Bewijs. We passen volledige inductie naar n toe. Voor n = 1 hebben we de stelling al bewezen. Stel dat de stelling geldt voor elk polynoom van n variabelen en dat P (x 1, x 2,..., x n, x n+1 ) = 0 voor alle (x 1, x 2,..., x n, x n+1 ). P (x 1, x 2,..., x n, x n+1 ) = A 0 + A 1 x n+1 + A 2 x 2 n A k x k n+1, waarin de A i polynomen zijn in x 1, x 2,..., x n. Voor elk stel (x 1, x 2,..., x n ) is P een polynoom in x n+1 dat identiek nul is. Dit betekent dat de coëfficiënten A i allemaal nul zijn. Elke A i is dus nul voor elk stel waarden van de variabelen x 1, x 2,..., x n. Volgens de inductieveronderstelling zijn dan alle coëfficiënten van elke A i nul, m.a.w. alle coëfficiënten van P zijn nul. Men gebruikt vaak polynomen in n variabelen waarbij de som k 1 + k k n voor alle termen c x k1 1 xk2 2 xkn n hetzelfde is. Zulke polynomen heten homogeen. Voorbeelden voor n = 3: 7x 3 1x 2 x 1 x 2 x x 2 2x x 4 2, x x 4 1x 2 + x 2 2x 3 3 en (x 1 + 2x 2 x 3 ) 8. Als in elke term k 1 + k k n = r, dan heet het polynoom homogeen van graad r. De voorbeelden hierboven zijn homogeen van respectievelijk graad 4, graad 5 en 5
19 graad 8. Het is duidelijk dat als P homogeen van graad r is, voor iedere waarde van t de gelijkheid geldt. Het omgekeerde is ook waar: P (tx 1, tx 2,..., tx n ) = t r P (x 1, x 2,..., x n ) (2) Stelling 3.2 Voldoet het polynoom P voor iedere t en elk stel (x 1, x 2,..., x n ) aan (2), dan is P homogeen van graad r. Bewijs. Kies een vast stel waarden (x 1, x 2,..., x n ); P (tx 1, tx 2,..., tx n ) is dan een polynoom in t: P (tx 1, tx 2,..., tx n ) = A 0 + A 1 t + A 2 t 2 +. Hierbij is A i de som van alle termen c x k1 1 xk2 2 xkn n met k 1 + k k n = i. Het polynoom in t P (tx 1, tx 2,..., tx n ) t r P (x 1, x 2,..., x n ) = A 0 +A 1 t+a 2 t 2 + +A r 1 t r 1 +(A r P (x 1, x 2,..., x n ))t r + A r+1 t r+1 + is identiek nul, dus alle coëfficiënten zijn nul. Er geldt dus A i = 0 als i r, en dit geldt voor elk stel waarden (x 1, x 2,..., x n ). De coëfficiënten van alle polynomen A i (x 1, x 2,..., x n ) met i r zijn dus allemaal nul, dus P is homogeen van graad r. Opgave 3.1 P (x 1, x 2,..., x n ) en Q(x 1, x 2,..., x n ) zijn homogene polynomen van graad r respectievelijk s. Bewijs dat het product van P en Q homogeen van graad r + s is. Wanneer is de som van P en Q ook homogeen? Opgave 3.2 Voor welke waarden van k bestaat er een polynoom P (x, y, z) zo, dat x 3 + y 3 + z 3 + kxyz = (x + y + z)p (x, y, z). Opgave 3.3 Het polynoom P (x, y) voldoet aan P (x, x) = 0 voor alle x. Bewijs dat er een polynoom Q(x, y) bestaat zo, dat P (x, y) = (x y)q(x, y). Opgave 3.4 Vind alle polynomen P (x, y) die voldoen aan de volgende eigenschappen: (1) er is een n N zo, dat voor alle x, y, t R geldt P (tx, ty) = t n P (x, y); (2) voor alle a, b, c R geldt P (a + b, c) + P (b + c, a) + P (c + a, b) = 0; (3) P (1, 0) = 1. 4 Gemengde opgaven Opgave 4.1 P (x) = (x a)(x b) k(x c)(x d) met a < c < b. (a) Bewijs dat als k = 1, P voor elke waarde van d hooguit één nulpunt heeft. (b) Bewijs dat als k < 1, P voor elke waarde van d precies twee nulpunten heeft. (NWO 1 e ronde, 1969) Opgave 4.2 Bepaal alle polynomen P en Q zo, dat voor alle x P (x) 3 + Q(x)P (x) 2 + (x 4 + 1)P (x) + x 3 + x = 0. 6
20 Opgave 4.3 Bewijs dat 1 + x x x 9999 deelbaar is door 1 + x + x x 9. Opgave 4.4 Bepaal alle gehele getallen a zo, dat (x a)(x 10) + 1 geschreven kan worden als (x b)(x c) met b en c geheel. Opgave 4.5 P is een zevendegraads polynoom met gehele coëfficiënten en voor zeven verschillende gehele waarden van de variabele x geldt P (x) 2 = 1. Bewijs dat P niet geschreven kan worden als product van twee polynomen met gehele coëfficiënten en positieve graad. Opgave 4.6 Een polynoom met gehele coëfficiënten neemt oneven gehele waarden aan in 0 en in 1. Bewijs dat geen van zijn nulpunten geheel is. Opgave 4.7 Bewijs dat alle rationale nulpunten van het polynoom met gehele coëfficiënten x n + a n 1 x n 1 + a n 2 x n a 0 (a n = 1!) geheel zijn. Opgave 4.8 a en b zijn reële getallen zo, dat de vergelijking x 4 +ax 3 +bx 2 +ax+1 = 0 minstens één oplossing heeft. Bepaal de minimale waarde van a 2 + b 2. (IWO 1973) 7
21 Lesbrief 4 Binomiaalcoëfficiënten, Differentiequotiënten en Getallenrijen 1 Binomiaalcoëfficiënten Het is bekend dat (a + b) 2 = a 2 + 2ab + b 2 en dat (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3. In het algemeen geldt (a + b) n = a n + C 1 a n 1 b + + C n 1 ab n 1 + b n voor zekere gehele coëfficiënten C 1, C 2,..., C n. Deze zogenaamde binomiaalcoëfficiënten ( (binomium = tweeterm) hangen af van n. De notatie voor C k is meestal n ) ( k, spreek uit n boven k. Aangevuld met n ) ( 0 = n ) n = 1 geldt dus Omdat geldt (a + b) n = ( ) n a n + 0 ( ) n a n 1 b ( ) n b n = n (a + b) n = (a + b)(a + b) n 1 (( ) ( ) n 1 n 1 = (a + b) a n 1 + a n 2 b ( ) ( ) ( ) n 1 n 1 n 1 = a n + a n 1 b + + ab n n 1 ( ) ( ) n 1 n 1 + a n 1 b + + ab n n 2 n k=0 ( ) n a n k b k. (1) k ( ) n 1 )b n 1 n 1 ( ) n 1 b n n 1 kan men de n-de binomiaalcoëfficiënten uitdrukken in de n 1-ste: ( ) ( ) ( ) n n 1 n 1 = + k k k 1 (2) Hierbij wordt ( ( p q) = 0 gesteld als q < 0 of als q > p. Samen met 1 ( 0) = 1 1) = 1 legt (2) de binomiaalcoëfficiënten volledig vast. Men berekent ze gemakkelijk met behulp van de driehoek van Pascal, waarin elk getal behalve de bovenste twee de som is van de twee getallen er schuin boven: n = 0 n = 1 n = 2 n = 3 n = 4 n =
22 Omdat a en b in (a + b) n symmetrisch voorkomen, geldt ( ) ( ) n n = k n k (3) De getallen ( n k) kunnen ook als volgt berekend worden: (a + b) n = (a + b)(a + b) (a + b) }{{} n maal Een term a n k b k ontstaat bij het haakjes wegwerken telkens als men in k factoren een b neemt en in de overige n k een a. ( n k) is dus gelijk aan het aantal manieren waarop men uit n elementen k elementen kan kiezen. Voor het eerste element kan men kiezen uit n mogelijkheden, voor het tweede uit n 1, enzovoorts. Dit geeft n(n 1) (n k + 1) mogelijkheden. Maar omdat de volgorde waarin het keuzeresultaat tot stand is gekomen niet van belang is, moet nog gedeeld worden door het aantal mogelijke permutaties van de gekozen k elementen, dit is k!. Er geldt dus: ( ) n n(n 1) (n k + 1) n! = = k k! k!(n k)!. (4). Opgave 1.1 Bewijs (4) met volledige inductie naar n door formule (2) te gebruiken. Enige eenvoudige identiteiten: n ( ) n (i) Kies in (1) a = b = 1: 2 n =. k k=0 n ( ) n (ii) Kies in (1) a = 1, b = 1: 0 = ( 1) k. k k=0 k ( ) ( ) n + i n k ( ) ( ) n + i n + 1 k ( ) n + i (iii) = + = + = i 0 i 0 i i=0 i=1 i=1 ( ) n + 2 k ( ) ( ) n + i n + k = = door herhaald toepassen van (2). 1 i k i=2 Toepassing. Onder p personen moet men n guldens verdelen (n p) zo, dat elk minstens één gulden krijgt. Op hoeveel manieren is dit mogelijk? Oplossing. Leg de n guldens op een rij. Er zijn dan n 1 tussenruimten. Vult men hiervan n p tussenruimten door schakels op, dan ontstaat een rij van p kettingen, voor elk persoon één. Het aantal mogelijke verdelingen is dus gelijk aan het aantal mogelijkheden om uit de n 1 tussenruimten er n p te kiezen: ( ) ( n 1 n p = n 1 p 1). Toepassing. Bewijs dat voor geen enkel niet-negatief geheel getal n geldt dat n k=0 ( ) 2n k 2k + 1 een vijfvoud is. (IWO 1974) Oplossing. Reken modulo 5. Dan geldt 2 3k (2 3 ) k 3 k mod 5. We proberen de binomiaalcoëfficiënten met behulp van (2) af te breken. Pas (2) twee maal toe, dan volgt ( ) 2n + 1 = 2k + 1 ( ) 2n k + 1 ( 2n 1 2k ) + ( ) 2n 1. 2k 1 2
23 Noem S n = n ( 2n+1 ) k=0 2k+1 3 k en T n = n lagere S-en en T -en uitdrukken. S n = T n = n ( ( ) ( 2n 1 2n k + 1 2k k=0 ) + n ( ( ) ( ) 2n 1 2n k 2k 1 k=0 k=0 ( 2n+1 ) 2k 3 k, dan kan men S n en T n in de ( ) 2n 1 ) 3 k = S n 1 + 2T n 1 + 3S n 1. 2k 1 ( ) 2n 1 ) 3 k = T n 1 + 6S n 1 + 3T n 1. 2k 2 Er geldt dus S n = 4S n 1 + 2T n 1 en T n = 6S n 1 + 4T n 1. Er zijn twee manieren om het bewijs te voltooien. (a) Er zijn modulo 5 voor S n en T n elk vijf mogelijkheden, dus er zijn hoogstens vijfentwintig mogelijke paren (S n, T n ). (S 0, T 0 ) = (1, 1) en met de hierboven afgeleide formules kan men de volgende paren berekenen. Na hoogstens vijfentwintig stappen moet periodiciteit optreden. Geldt dus voor geen enkele n < 25 dat S n 0 mod 5, dan is het bewijs geleverd. (b) We rekenen steeds modulo 5: S n = 4S n 1 + 2T n 1 S n 1 + 2T n 1 en T n = 6S n 1 + 4T n 1 S n 1 T n 1. Daarom S n S n 1 + 2T n 1 S n 2 2T n 2 + 2S n 2 2T n 2 3S n 2 4T n 2 3S n 2 + T n 2 3S n 3 + 6T n 3 3S n 3 +6T n 3 +S n 3 T n 3 2S n 3. Men berekent dan S 0 = 1, S 1 1 mod 5, S 2 1 mod 5 en aangezien ( 2) k 0 mod 5 voor alle k, is ook S n 0 mod 5 voor alle k. 2 Differentiequotiënten Laat gegeven zijn het n-de graads polynoom P (x) = a n x n + + a 0, a n 0. Het differentiequotiënt h1 P (x) := P (x + h 1) P (x) h 1 = (a n(x + h 1 ) n + + a 0 ) (a n x n + + a 0 ) h 1 = a n nx n 1 + behorende bij een vaste toename h 1 0, is een (n 1) e -graads polynoom met a n n als coëfficiënt van de hoogste macht van x. (Verifieer dit door uitwerken.) Van dit polynoom vormt men het differentiequotiënt bij een toename h 2 0: h2 ( h1 P (x) = h 1 P (x + h 2 ) h1 P (x) h 2 = a n n(n 1)x n 2 +. Dit differentiequotiënt wordt genoteerd als h2h 1 P (x). Het is een polynoom van graad n 2 in x. In het algemeen wordt het k-de differentiequotiënt behorende bij de toenames h 1, h 2,..., h k gedefinieerd door hk h k 1 h 1 P (x) := h k 1 h 1 P (x + h k ) hk 1 h 1 P (x) h k. Het is een polynoom in x van de vorm a n n(n 1) (n k + 1)x n k +. In het bijzonder geldt voor k = n hn h 1 P (x) = a n n!. Dit is dus een constante, die afhankelijk is van de waarden van h 1, h 2,..., h n. Er geldt daarom 3
24 Stelling 2.1 Van een n-de graads polynoom met kopcoëfficiënt a n is het n-de differentiequotiënt gelijk aan a n n!. De hogere differentiequotiënten zijn nul. Kies h 1 = h 2 = = h n = 1 en schrijf i in plaats van 11 }{{ 1, dan volgt } i maal 1 P (x) = P (x + 1) P (x), 2 P (x) = P (x + 2) P (x + 1) (P (x + 1) P (x)) = P (x + 2) 2P (x + 1) + P (x), 3 ( ) 3 3 P (x) = P (x + 3) 3P (x + 2) + 3P (x + 1) P (x) = ( 1) k P (x + 3 k). k Zo voortgaande ontstaat ten slotte a n n! = n P (x) = k=0 k=0 n ( ) n ( 1) k P (x + n k). k Door de substitutie x = x + c ontstaat uit een polynoom in x a n x n + + a 0 = a n ( x + c) n + = a n x n + een polynoom in x van dezelfde graad en met dezelfde kopcoëfficiënt. (De andere coëfficiënten zijn in het algemeen anders.) Op grond hiervan kan men bovenstaande formule nog iets vereenvoudigen door x + n in plaats van x als variabele te nemen. Stelling 2.2 Voor elk polynoom Q(x) = a n x n + + a 0 geldt n ( ) n ( 1) k Q(x k) = a n n!. k k=0 Opgave 2.1 Verifieer dat stelling (2.2) ook geldt als a n = 0. Opgave 2.2 Bewijs de volgende identiteiten: n ( ) n (1) ( 1) k (x k) n = n!. k k=0 n ( ) n (2) ( 1) k (2 n+1 n k 1) n = n!. k k=0 n ( ) n (3) ( 1) n k (A + Bk) p = B n n!alsp=n.0als0 p < n, p geheel. k (4) (5) k=0 2m ( )( ) m 2m k ( 1) 2m k = (2m)! k 2 2 m. n ( )( ) n kp ( 1) n k = p n als p een positief geheel getal is. k n k=0 k=0 3 Getallenrijen Een rij reële getallen a 1, a 2, a 3,... wordt vaak genoteerd als {a i } i=1 of, als er geen verwarring mogelijk is, kortweg {a i }. 4
25 Definitie 3.1 De rij {a i } convergeert naar het getal k (ook wel: heeft limiet k) als er bij elk positief getal ε een getal I gevonden kan worden zo, dat voor alle termen a i uit de rij met i > I geldt a i k < ε. Notatie: lim i a i = k (ook wel: a i k als i ). Elke rij die niet convergeert heet divergent. Er zijn bijzondere divergente rijen: Definitie 3.2 De rij {a i } divergeert naar plus oneindig (ook wel: heeft limiet plus oneindig) als er bij elk getal M een getal I is zo, dat voor alle i > I geldt dat a i > M. Notatie: lim i a i = + (of: a i + als i ). De rij {a i } divergeert naar min oneindig (of: heeft limiet min oneindig) als de rij { a i } naar plus oneindig divergeert. Notatie: lim i a i = (of: a i als i ). Opmerking: plus oneindig en min oneindig zijn dus geen reële getallen, maar uitdrukkingen om het gedrag van bepaalde rijen kort te kunnen beschrijven. Voorbeelden: 1. a i = 1 i. De rij { 1 i } convergeert naar a i = i+1 i. De rij { i+1 i } convergeert naar a i = i 2. De rij {i 2 } divergeert naar a i = ( 1) i. De rij {( 1) i } divergeert zonder limiet. 3.1 Rekenkundige rijen Een rij van de vorm a, a + k, a + 2k, a + 3k,... heet een rekenkundige rij. De som van de eerste n + 1 termen bepaalt men als volgt: a + (a + nk) = 2a + nk, (a + k) + (a + (n 1)k) = 2a + nk,...,(a + nk) + a = 2a + nk. Daarom 2 ( a + (a + k) + + (a + nk) ) = (a + (a + nk)) + ((a + k) + (a + (n 1)k)) + + ((a + nk) + a) = (2a + nk) + (2a + nk) + + (2a + nk). Hieruit blijkt dat }{{} n+1 maal a + (a + k) + + (a + nk) = 1 2 (n + 1)(2a + nk). 3.2 Meetkundige rijen Een rij van de vorm a, ar, ar 2, ar 3,... heet een meetkundige rij met reden (ratio) r. r is de verhouding tussen twee opeenvolgende termen. De som S n van de eerste n termen bepaalt men als volgt: S n = a + ar + + ar n 1 rs n = ar + + ar n 1 + ar n (1 r)s n = a(1 r n ) Hieruit volgt dat als r 1, dan geldt S n = 1 rn 1 r. (5) In het algemeen noemt men de som S n = a 1 + a a n = n i=1 a i de n-de partiële som van de rij {a i }. De rij {S n } n=1 van partiële sommen noemt men een 5
Getaltheorie II. ax + by = c, a, b, c Z (1)
 Lesbrief 2 Getaltheorie II 1 Lineaire vergelijkingen Een vergelijking van de vorm ax + by = c, a, b, c Z (1) heet een lineaire vergelijking. In de getaltheorie gaat het er slechts om gehele oplossingen
Lesbrief 2 Getaltheorie II 1 Lineaire vergelijkingen Een vergelijking van de vorm ax + by = c, a, b, c Z (1) heet een lineaire vergelijking. In de getaltheorie gaat het er slechts om gehele oplossingen
Getaltheorie I. c = c 1 = 1 c (1)
 Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Polynomen. + 5x + 5 \ 3 x 1 = S(x) 2x x. 3x x 3x 2 + 2
 Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P () = a n n + a n 1 n 1 + + a 1 + a 0, (a n 0), heet een polynoom of veelterm in de variabele. Het getal n heet de graad van
Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P () = a n n + a n 1 n 1 + + a 1 + a 0, (a n 0), heet een polynoom of veelterm in de variabele. Het getal n heet de graad van
Differentiequotiënten en Getallenrijen
 Lesbrief 4 Binomiaalcoëfficiënten, Differentiequotiënten en Getallenrijen Binomiaalcoëfficiënten Het is beend dat (a + b 2 = a 2 + 2ab + b 2 en dat (a + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3. In het algemeen
Lesbrief 4 Binomiaalcoëfficiënten, Differentiequotiënten en Getallenrijen Binomiaalcoëfficiënten Het is beend dat (a + b 2 = a 2 + 2ab + b 2 en dat (a + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3. In het algemeen
7.1 Het aantal inverteerbare restklassen
 Hoofdstuk 7 Congruenties in actie 7.1 Het aantal inverteerbare restklassen We pakken hier de vraag op waarmee we in het vorige hoofdstuk geëindigd zijn, namelijk hoeveel inverteerbare restklassen modulo
Hoofdstuk 7 Congruenties in actie 7.1 Het aantal inverteerbare restklassen We pakken hier de vraag op waarmee we in het vorige hoofdstuk geëindigd zijn, namelijk hoeveel inverteerbare restklassen modulo
3 Modulorekenen. 3.1 De eulerfunctie en de kleine stelling van Fermat. Oefening 3.1. Bepaal Φ(1992), Φ(2011) en Φ(2048) (83 en 2011 zijn priem).
 3 Modulorekenen 3.1 De eulerfunctie en de kleine stelling van Fermat Oefening 3.1. Bepaal Φ(1992), Φ(2011) en Φ(2048) (83 en 2011 zijn priem). Oplossing 3.1 1992 = 2 3 3 83. Φ(1992) = 2 2 2 82 = 656. 2048
3 Modulorekenen 3.1 De eulerfunctie en de kleine stelling van Fermat Oefening 3.1. Bepaal Φ(1992), Φ(2011) en Φ(2048) (83 en 2011 zijn priem). Oplossing 3.1 1992 = 2 3 3 83. Φ(1992) = 2 2 2 82 = 656. 2048
2 n 1. OPGAVEN 1 Hoeveel cijfers heeft het grootste bekende Mersenne-priemgetal? Met dit getal vult men 320 krantenpagina s.
 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Getallenleer Inleiding op codeertheorie. Cursus voor de vrije ruimte
 Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
Oefening 4.3. Zoek een positief natuurlijk getal zodanig dat de helft een kwadraat is, een derde is een derdemacht en een vijfde is een vijfdemacht.
 4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
Oefening 4.3. Zoek een positief natuurlijk getal zodanig dat de helft een kwadraat is, een derde is een derdemacht en een vijfde is een vijfdemacht.
 4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 = 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 = 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
1 Delers 1. 3 Grootste gemene deler en kleinste gemene veelvoud 12
 Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
Zomercursus Wiskunde. Module 1 Algebraïsch rekenen (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 011 Module 1 Algebraïsch rekenen (versie augustus 011) Inhoudsopgave 1 Rekenen met haakjes 1.1 Uitwerken van haakjes en ontbinden in factoren............. 1. De
Katholieke Universiteit Leuven September 011 Module 1 Algebraïsch rekenen (versie augustus 011) Inhoudsopgave 1 Rekenen met haakjes 1.1 Uitwerken van haakjes en ontbinden in factoren............. 1. De
OPLOSSINGEN VAN DE OEFENINGEN
 OPLOSSINGEN VAN DE OEFENINGEN 1.3.1. Er zijn 42 mogelijke vercijferingen. 2.3.4. De uitkomsten zijn 0, 4 en 4 1 = 4. 2.3.6. Omdat 10 = 1 in Z 9 vinden we dat x = c 0 +... + c m = c 0 +... + c m. Het getal
OPLOSSINGEN VAN DE OEFENINGEN 1.3.1. Er zijn 42 mogelijke vercijferingen. 2.3.4. De uitkomsten zijn 0, 4 en 4 1 = 4. 2.3.6. Omdat 10 = 1 in Z 9 vinden we dat x = c 0 +... + c m = c 0 +... + c m. Het getal
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 008 Algebraïsch rekenen (versie 7 juni 008) Inleiding In deze module worden een aantal basisrekentechnieken herhaald. De nadruk ligt vooral op het symbolisch rekenen.
Katholieke Universiteit Leuven September 008 Algebraïsch rekenen (versie 7 juni 008) Inleiding In deze module worden een aantal basisrekentechnieken herhaald. De nadruk ligt vooral op het symbolisch rekenen.
Dossier 3 PRIEMGETALLEN
 Dossier 3 PRIEMGETALLEN atomen van de getallenleer Dr. Luc Gheysens Een priemgetal is een natuurlijk getal met twee verschillende delers, nl. 1 en het getal zelf. De priemgetallen zijn dus 2, 3, 5, 7,
Dossier 3 PRIEMGETALLEN atomen van de getallenleer Dr. Luc Gheysens Een priemgetal is een natuurlijk getal met twee verschillende delers, nl. 1 en het getal zelf. De priemgetallen zijn dus 2, 3, 5, 7,
Getaltheorie groep 3: Primitieve wortels
 Getaltheorie groep 3: Primitieve wortels Trainingsweek juni 2008 Inleiding Voor a relatief priem met m hebben we de orde van a modulo m gedefinieerd als ord m (a) = min { n Z + a n 1 (mod m) }. De verzameling
Getaltheorie groep 3: Primitieve wortels Trainingsweek juni 2008 Inleiding Voor a relatief priem met m hebben we de orde van a modulo m gedefinieerd als ord m (a) = min { n Z + a n 1 (mod m) }. De verzameling
Universiteit Gent. Academiejaar Discrete Wiskunde. 1ste kandidatuur Informatica. Collegenota s. Prof. Dr.
 Universiteit Gent Academiejaar 2001 2002 Discrete Wiskunde 1ste kandidatuur Informatica Collegenota s Prof. Dr. Frank De Clerck Herhalingsoefeningen 1. Bepaal het quotiënt en de rest van de deling van
Universiteit Gent Academiejaar 2001 2002 Discrete Wiskunde 1ste kandidatuur Informatica Collegenota s Prof. Dr. Frank De Clerck Herhalingsoefeningen 1. Bepaal het quotiënt en de rest van de deling van
Hoofdstuk 6. Congruentierekening. 6.1 Congruenties
 Hoofdstuk 6 Congruentierekening 6.1 Congruenties We hebben waarschijnlijk allemaal wel eens opgemerkt dat bij vermenigvuldigen van twee getallen de laatste cijfers als het ware meevermenigvuldigen. Stel
Hoofdstuk 6 Congruentierekening 6.1 Congruenties We hebben waarschijnlijk allemaal wel eens opgemerkt dat bij vermenigvuldigen van twee getallen de laatste cijfers als het ware meevermenigvuldigen. Stel
1.5.1 Natuurlijke, gehele en rationale getallen
 46 Getallen 1.5 Getaltheorie 1.5.1 Natuurlijke, gehele en rationale getallen De getallen 0,1,2,3,4,... enz. worden de natuurlijke getallen genoemd (de heleverzamelingvanaldezegetallenbijelkaarnoterenwemethetteken:
46 Getallen 1.5 Getaltheorie 1.5.1 Natuurlijke, gehele en rationale getallen De getallen 0,1,2,3,4,... enz. worden de natuurlijke getallen genoemd (de heleverzamelingvanaldezegetallenbijelkaarnoterenwemethetteken:
Getallen, 2e druk, extra opgaven
 Getallen, 2e druk, extra opgaven Frans Keune november 2010 De tweede druk bevat 74 nieuwe opgaven. De nummering van de opgaven van de eerste druk is in de tweede druk dezelfde: nieuwe opgaven staan in
Getallen, 2e druk, extra opgaven Frans Keune november 2010 De tweede druk bevat 74 nieuwe opgaven. De nummering van de opgaven van de eerste druk is in de tweede druk dezelfde: nieuwe opgaven staan in
Veeltermen. Module 2. 2.1 Definitie en voorbeelden. Een veelterm met reële coëfficiënten in één veranderlijke x is een uitdrukking van de vorm
 Module 2 Veeltermen 2.1 Definitie en voorbeelden Een veelterm met reële coëfficiënten in één veranderlijke x is een uitdrukking van de vorm a 0 +a 1 x+a 2 x 2 + +a n x n met a 0,a 1,a 2,...,a n Ê en n
Module 2 Veeltermen 2.1 Definitie en voorbeelden Een veelterm met reële coëfficiënten in één veranderlijke x is een uitdrukking van de vorm a 0 +a 1 x+a 2 x 2 + +a n x n met a 0,a 1,a 2,...,a n Ê en n
Je hebt twee uur de tijd voor het oplossen van de vraagstukken. µkw uitwerkingen. 12 juni 2015
 Je hebt twee uur de tijd voor het oplossen van de vraagstukken. Elk vraagstuk is maximaal 10 punten waard. Begin elke opgave op een nieuw vel papier. µkw uitwerkingen 12 juni 2015 Vraagstuk 1. We kunnen
Je hebt twee uur de tijd voor het oplossen van de vraagstukken. Elk vraagstuk is maximaal 10 punten waard. Begin elke opgave op een nieuw vel papier. µkw uitwerkingen 12 juni 2015 Vraagstuk 1. We kunnen
We beginnen met de eigenschappen van de gehele getallen.
 II.2 Gehele getallen We beginnen met de eigenschappen van de gehele getallen. Axioma s voor Z De gegevens zijn: (a) een verzameling Z; (b) elementen 0 en 1 in Z; (c) een afbeelding +: Z Z Z, de optelling;
II.2 Gehele getallen We beginnen met de eigenschappen van de gehele getallen. Axioma s voor Z De gegevens zijn: (a) een verzameling Z; (b) elementen 0 en 1 in Z; (c) een afbeelding +: Z Z Z, de optelling;
Complexe e-macht en complexe polynomen
 Aanvulling Complexe e-macht en complexe polynomen Dit stuk is een uitbreiding van Appendix I, Complex Numbers De complexe e-macht wordt ingevoerd en het onderwerp polynomen wordt in samenhang met nulpunten
Aanvulling Complexe e-macht en complexe polynomen Dit stuk is een uitbreiding van Appendix I, Complex Numbers De complexe e-macht wordt ingevoerd en het onderwerp polynomen wordt in samenhang met nulpunten
RSA. F.A. Grootjen. 8 maart 2002
 RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
Eigenschap (Principe van welordening) Elke niet-lege deelverzameling V N bevat een kleinste element.
 Hoofdstuk 2 De regels van het spel 2.1 De gehele getallen Grof gezegd kunnen we de (elementaire) getaltheorie omschrijven als de wiskunde van de getallen 1, 2, 3, 4,... die we ook de natuurlijke getallen
Hoofdstuk 2 De regels van het spel 2.1 De gehele getallen Grof gezegd kunnen we de (elementaire) getaltheorie omschrijven als de wiskunde van de getallen 1, 2, 3, 4,... die we ook de natuurlijke getallen
Bewijs door inductie
 Bewijs door inductie 1 Bewijs door inductie Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Als je wilt weten of iets waar is voor alle natuurlijke
Bewijs door inductie 1 Bewijs door inductie Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Als je wilt weten of iets waar is voor alle natuurlijke
Uitwerkingen toets 12 juni 2010
 Uitwerkingen toets 12 juni 2010 Opgave 1. Bekijk rijen a 1, a 2, a 3,... van positieve gehele getallen. Bepaal de kleinst mogelijke waarde van a 2010 als gegeven is: (i) a n < a n+1 voor alle n 1, (ii)
Uitwerkingen toets 12 juni 2010 Opgave 1. Bekijk rijen a 1, a 2, a 3,... van positieve gehele getallen. Bepaal de kleinst mogelijke waarde van a 2010 als gegeven is: (i) a n < a n+1 voor alle n 1, (ii)
6 Ringen, lichamen, velden
 6 Ringen, lichamen, velden 6.1 Polynomen over F p : irreducibiliteit en factorisatie Oefening 6.1. Bewijs dat x 2 + 2x + 2 irreducibel is in Z 3 [x]. Oplossing 6.1 Aangezien de veelterm van graad 3 is,
6 Ringen, lichamen, velden 6.1 Polynomen over F p : irreducibiliteit en factorisatie Oefening 6.1. Bewijs dat x 2 + 2x + 2 irreducibel is in Z 3 [x]. Oplossing 6.1 Aangezien de veelterm van graad 3 is,
Priemontbinding en ggd s
 Hoofdstuk 3 Priemontbinding en ggd s 3.1 Priemgetallen Een getal > 1 dat alleen 1 en zichzelf als positieve deler heeft noemen we een priemgetal. De rij priemgetallen begint als volgt, 2, 3, 5, 7, 11,
Hoofdstuk 3 Priemontbinding en ggd s 3.1 Priemgetallen Een getal > 1 dat alleen 1 en zichzelf als positieve deler heeft noemen we een priemgetal. De rij priemgetallen begint als volgt, 2, 3, 5, 7, 11,
IMO-selectietoets I donderdag 1 juni 2017
 IMO-selectietoets I donderdag 1 juni 2017 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een positief geheel getal. Gegeven zijn cirkelvormige schijven met stralen 1, 2,..., n. Van
IMO-selectietoets I donderdag 1 juni 2017 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een positief geheel getal. Gegeven zijn cirkelvormige schijven met stralen 1, 2,..., n. Van
Wiskunde klas 3. Vaardigheden. Inhoudsopgave. 1. Breuken 2. 2. Gelijksoortige termen samennemen 3. 3. Rekenen met machten 3. 4. Rekenen met wortels 4
 Vaardigheden Wiskunde klas Inhoudsopgave. Breuken. Gelijksoortige termen samennemen. Rekenen met machten. Rekenen met wortels. Algebraïsche producten 6. Ontbinden in factoren 6 7. Eerstegraads vergelijkingen
Vaardigheden Wiskunde klas Inhoudsopgave. Breuken. Gelijksoortige termen samennemen. Rekenen met machten. Rekenen met wortels. Algebraïsche producten 6. Ontbinden in factoren 6 7. Eerstegraads vergelijkingen
1 Limiet van een rij Het begrip rij Bepaling van een rij Expliciet voorschrift Recursief voorschrift 3
 HOOFDSTUK 6: RIJEN 1 Limiet van een rij 2 1.1 Het begrip rij 2 1.2 Bepaling van een rij 2 1.2.1 Expliciet voorschrift 2 1.2.2 Recursief voorschrift 3 1.2.3 Andere gevallen 3 1.2.4 Rijen met de grafische
HOOFDSTUK 6: RIJEN 1 Limiet van een rij 2 1.1 Het begrip rij 2 1.2 Bepaling van een rij 2 1.2.1 Expliciet voorschrift 2 1.2.2 Recursief voorschrift 3 1.2.3 Andere gevallen 3 1.2.4 Rijen met de grafische
V.4 Eigenschappen van continue functies
 V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
Oplossing van opgave 6 en van de kerstbonusopgave.
 Oplossing van opgave 6 en van de kerstbonusopgave. Opgave 6 Lesbrief, opgave 4.5 De getallen m en n zijn verschillende positieve gehele getallen zo, dat de laatste drie cijfers van 1978 m en 1978 n overeenstemmen.
Oplossing van opgave 6 en van de kerstbonusopgave. Opgave 6 Lesbrief, opgave 4.5 De getallen m en n zijn verschillende positieve gehele getallen zo, dat de laatste drie cijfers van 1978 m en 1978 n overeenstemmen.
Algebra groep 2 & 3: Standaardtechnieken kwadratische functies
 Algebra groep 2 & 3: Standaardtechnieken kwadratische functies Trainingsweek juni 2008 Kwadraat afsplitsen Een kwadratische functie oftewel tweedegraads polynoom) px) = ax 2 + bx + c a 0) kan in verschillende
Algebra groep 2 & 3: Standaardtechnieken kwadratische functies Trainingsweek juni 2008 Kwadraat afsplitsen Een kwadratische functie oftewel tweedegraads polynoom) px) = ax 2 + bx + c a 0) kan in verschillende
Bijzondere kettingbreuken
 Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
7 Deelbaarheid. 7.1 Deelbaarheid WIS7 1
 WIS7 1 7 Deelbaarheid 7.1 Deelbaarheid Deelbaarheid Voor geheeltallige d en n met d > 0 zeggen we dat d een deler is van n, en ook dat n deelbaar is door d, als n d een geheel getal is. Notatie: d\n k
WIS7 1 7 Deelbaarheid 7.1 Deelbaarheid Deelbaarheid Voor geheeltallige d en n met d > 0 zeggen we dat d een deler is van n, en ook dat n deelbaar is door d, als n d een geheel getal is. Notatie: d\n k
Diophantische vergelijkingen
 Diophantische vergelijkingen 1 Wat zijn Diophantische vergelijkingen? Een Diophantische vergelijking is een veeltermvergelijking waarbij zowel de coëfficiënten als de oplossingen gehele getallen moeten
Diophantische vergelijkingen 1 Wat zijn Diophantische vergelijkingen? Een Diophantische vergelijking is een veeltermvergelijking waarbij zowel de coëfficiënten als de oplossingen gehele getallen moeten
Inleiding tot de Problem Solving - deel 1: Combinatoriek en getaltheorie
 Inleiding tot de Problem Solving - deel 1: Combinatoriek en getaltheorie Jan Vonk 1 oktober 2008 1 Combinatoriek Inleiding Een gebied dat vandaag de dag haast niet onderschat kan worden binnen de wiskunde
Inleiding tot de Problem Solving - deel 1: Combinatoriek en getaltheorie Jan Vonk 1 oktober 2008 1 Combinatoriek Inleiding Een gebied dat vandaag de dag haast niet onderschat kan worden binnen de wiskunde
Hoofdstuk 12. Sommen van kwadraten. 12.1 Sommen van twee kwadraten
 Hoofdstuk 12 Sommen van kwadraten 12.1 Sommen van twee kwadraten In Hoofdstuk 11 hebben we gezien dat als p een oneven priemdeler van a 2 + b 2 is, en p deelt niet zowel a als b, dan is p gelijk aan 1
Hoofdstuk 12 Sommen van kwadraten 12.1 Sommen van twee kwadraten In Hoofdstuk 11 hebben we gezien dat als p een oneven priemdeler van a 2 + b 2 is, en p deelt niet zowel a als b, dan is p gelijk aan 1
Opgaven Eigenschappen van Getallen Security, 2018, Werkgroep.
 Opgaven Eigenschappen van Getallen Security, 2018, Werkgroep. Gebruik deze opgaven, naast die uit het boek, om de stof te oefenen op het werkcollege. Cijfer: Op een toets krijg je meestal zes tot acht
Opgaven Eigenschappen van Getallen Security, 2018, Werkgroep. Gebruik deze opgaven, naast die uit het boek, om de stof te oefenen op het werkcollege. Cijfer: Op een toets krijg je meestal zes tot acht
Memoriseren: Een getal is deelbaar door 10 als het laatste cijfer een 0 is. Of: Een getal is deelbaar door 10 als het eindigt op 0.
 REKENEN VIJFDE KLAS en/of ZESDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Luc Cielen: Regels van deelbaarheid, grootste gemene deler en kleinste gemeen veelvoud 1 Deelbaarheid door 10, 100, 1000. Door
REKENEN VIJFDE KLAS en/of ZESDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Luc Cielen: Regels van deelbaarheid, grootste gemene deler en kleinste gemeen veelvoud 1 Deelbaarheid door 10, 100, 1000. Door
III.2 De ordening op R en ongelijkheden
 III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
III.2 De ordening op R en ongelijkheden In de vorige paragraaf hebben we axioma s gegeven voor de optelling en vermenigvuldiging in R, maar om R vast te leggen moeten we ook ongelijkheden in R beschouwen.
Definitie 5.1. Cyclische groepen zijn groepen voortgebracht door 1 element.
 Hoofdstuk 5 Cyclische groepen 5.1 Definitie Definitie 5.1. Cyclische groepen zijn groepen voortgebracht door 1 element. Als G wordt voortgebracht door a en a n = e, dan noteren we de groep als C n = a.
Hoofdstuk 5 Cyclische groepen 5.1 Definitie Definitie 5.1. Cyclische groepen zijn groepen voortgebracht door 1 element. Als G wordt voortgebracht door a en a n = e, dan noteren we de groep als C n = a.
Uitwerkingen toets 9 juni 2012
 Uitwerkingen toets 9 juni 0 Opgave. Voor positieve gehele getallen a en b definiëren we a b = a b ggd(a, b). Bewijs dat voor elk geheel getal n > geldt: n is een priemmacht (d.w.z. dat n te schrijven is
Uitwerkingen toets 9 juni 0 Opgave. Voor positieve gehele getallen a en b definiëren we a b = a b ggd(a, b). Bewijs dat voor elk geheel getal n > geldt: n is een priemmacht (d.w.z. dat n te schrijven is
FACTORISATIE EN CRYPTOGRAFIE
 FACTORISATIE EN CRYPTOGRAFIE UvA-MASTERCLASS WISKUNDE 1993 P. Stevenhagen Faculteit Wiskunde en Informatica Universiteit van Amsterdam 1993 INLEIDING In deze masterclass zullen we ons voornamelijk bezighouden
FACTORISATIE EN CRYPTOGRAFIE UvA-MASTERCLASS WISKUNDE 1993 P. Stevenhagen Faculteit Wiskunde en Informatica Universiteit van Amsterdam 1993 INLEIDING In deze masterclass zullen we ons voornamelijk bezighouden
Volledige inductie. Hoofdstuk 7. Van een deelverzameling V van de verzameling N van alle natuurlijke getallen veronderstellen.
 Hoofdstuk 7 Volledige inductie Van een deelverzameling V van de verzameling N van alle natuurlijke getallen veronderstellen we het volgende: (i) 0 V (ii) k N k V k + 1 V Dan is V = N. Men ziet dit als
Hoofdstuk 7 Volledige inductie Van een deelverzameling V van de verzameling N van alle natuurlijke getallen veronderstellen we het volgende: (i) 0 V (ii) k N k V k + 1 V Dan is V = N. Men ziet dit als
1. REGELS VAN DEELBAARHEID.
 REKENEN VIJFDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Deelbaarheid door 10, 100, 1000 10: het laatste cijfer (= cijfer van de eenheden) is 0 100: laatste twee cijfers zijn 0 (cijfers van de eenheden
REKENEN VIJFDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Deelbaarheid door 10, 100, 1000 10: het laatste cijfer (= cijfer van de eenheden) is 0 100: laatste twee cijfers zijn 0 (cijfers van de eenheden
PG blok 4 werkboek bijeenkomst 4 en 5
 2015-2015 PG blok 4 werkboek bijeenkomst 4 en 5 Inhoud Kenmerken van deelbaarheid (herhaling)...1 Ontbinden in factoren...1 Priemgetallen (herhaling)...2 Ontbinden in priemfactoren...2 KGV (Kleinste Gemene
2015-2015 PG blok 4 werkboek bijeenkomst 4 en 5 Inhoud Kenmerken van deelbaarheid (herhaling)...1 Ontbinden in factoren...1 Priemgetallen (herhaling)...2 Ontbinden in priemfactoren...2 KGV (Kleinste Gemene
Uitwerking Puzzel 93-1, Doelloos
 Uitwerking Puzzel 93-1, Doelloos Wobien Doyer Lieke de Rooij Volgens de titel is deze puzzel zonder doel, dus zonder bekende toepassing. Het doel is echter nul en dat is zeker in de wiskunde niet niks.
Uitwerking Puzzel 93-1, Doelloos Wobien Doyer Lieke de Rooij Volgens de titel is deze puzzel zonder doel, dus zonder bekende toepassing. Het doel is echter nul en dat is zeker in de wiskunde niet niks.
Wanneer zijn veelvouden van proniks proniks?
 1 Uitwerking puzzel 92-1 Wanneer zijn veelvouden van proniks proniks? Harm Bakker noemde het: pro-niks voor-niks De puzzel was voor een groot deel afkomstig van Frits Göbel. Een pronik is een getal dat
1 Uitwerking puzzel 92-1 Wanneer zijn veelvouden van proniks proniks? Harm Bakker noemde het: pro-niks voor-niks De puzzel was voor een groot deel afkomstig van Frits Göbel. Een pronik is een getal dat
Rekenen met cijfers en letters
 Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Pijlenklokken. 1 Inleiding
 Pijlenklokken 1 Inleiding In bovenstaande tekening zie je 1 rode punten. Er staan blauwe pijlen van elk rood punt naar een ander rood punt 4 plaatsen verder op de cirkel. Een dergelijke afbeelding noemen
Pijlenklokken 1 Inleiding In bovenstaande tekening zie je 1 rode punten. Er staan blauwe pijlen van elk rood punt naar een ander rood punt 4 plaatsen verder op de cirkel. Een dergelijke afbeelding noemen
Opgeloste en onopgeloste mysteries in de getaltheorie
 Opgeloste en onopgeloste mysteries in de getaltheorie Jan De Beule, Tom De Medts en Jeroen Demeyer Voorwoord 1 Voorwoord Beste leerling, Deze nota s zijn bedoeld als begeleiding bij 6 lesuren Opgeloste
Opgeloste en onopgeloste mysteries in de getaltheorie Jan De Beule, Tom De Medts en Jeroen Demeyer Voorwoord 1 Voorwoord Beste leerling, Deze nota s zijn bedoeld als begeleiding bij 6 lesuren Opgeloste
Combinatoriek groep 1
 Combinatoriek groep 1 Recursie Trainingsdag 3, 2 april 2009 Getallenrijen We kunnen een rij getallen a 0, a 1, a 2,... op twee manieren definiëren: direct of recursief. Een directe formule geeft a n in
Combinatoriek groep 1 Recursie Trainingsdag 3, 2 april 2009 Getallenrijen We kunnen een rij getallen a 0, a 1, a 2,... op twee manieren definiëren: direct of recursief. Een directe formule geeft a n in
Opmerking. TI1300 Redeneren en Logica. Met voorbeelden kun je niks bewijzen. Directe en indirecte bewijzen
 Opmerking TI1300 Redeneren en Logica College 2: Bewijstechnieken Tomas Klos Algoritmiek Groep Voor alle duidelijkheid: Het is verre van triviaal om definities te leren hanteren, beweringen op te lossen,
Opmerking TI1300 Redeneren en Logica College 2: Bewijstechnieken Tomas Klos Algoritmiek Groep Voor alle duidelijkheid: Het is verre van triviaal om definities te leren hanteren, beweringen op te lossen,
Hoofdstuk 3. Equivalentierelaties. 3.1 Modulo Rekenen
 Hoofdstuk 3 Equivalentierelaties SCHAUM 2.8: Equivalence Relations Twee belangrijke voorbeelden van equivalentierelaties in de informatica: resten (modulo rekenen) en cardinaliteit (aftelbaarheid). 3.1
Hoofdstuk 3 Equivalentierelaties SCHAUM 2.8: Equivalence Relations Twee belangrijke voorbeelden van equivalentierelaties in de informatica: resten (modulo rekenen) en cardinaliteit (aftelbaarheid). 3.1
handleiding ontbinden
 handleiding ontbinden inhoudsopgave inhoudsopgave de grote lijn 3 Bespreking per paragraaf 4 Applets 4 1 met gegeven product 4 ontbinden van getallen 4 3 vergelijkingen 5 4 onderzoek 6 tijdpad 9 materialen
handleiding ontbinden inhoudsopgave inhoudsopgave de grote lijn 3 Bespreking per paragraaf 4 Applets 4 1 met gegeven product 4 ontbinden van getallen 4 3 vergelijkingen 5 4 onderzoek 6 tijdpad 9 materialen
Definitie 1.1. Een groep is een verzameling G, uitgerust met een bewerking waarvoor geldt dat:
 Hoofdstuk 1 Eerste begrippen 1.1 Wat is een groep? Definitie 1.1. Een groep is een verzameling G, uitgerust met een bewerking waarvoor geldt dat: 1. a, b G : a b G 2. a, b, c G : a (b c) = (a b) c = a
Hoofdstuk 1 Eerste begrippen 1.1 Wat is een groep? Definitie 1.1. Een groep is een verzameling G, uitgerust met een bewerking waarvoor geldt dat: 1. a, b G : a b G 2. a, b, c G : a (b c) = (a b) c = a
Uitwerkingen Rekenen met cijfers en letters
 Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Selectietoets vrijdag 10 maart 2017
 Selectietoets vrijdag 10 maart 2017 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een even positief geheel getal. Een rijtje van n reële getallen noemen we volledig als voor elke gehele
Selectietoets vrijdag 10 maart 2017 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een even positief geheel getal. Een rijtje van n reële getallen noemen we volledig als voor elke gehele
12. Uitwerkingen van de opgaven
 12. Uitwerkingen van de opgaven 12.1. Uitwerkingen opgaven van hoofdstuk 3 Opgave 3.1 3,87 0,152 641, 2 Bereken met behulp van Maxima: 2,13 7,29 78 0,62 45 (%i1) 3.87*0.152*641.2/(2.13*7.29*78*0.62*45);
12. Uitwerkingen van de opgaven 12.1. Uitwerkingen opgaven van hoofdstuk 3 Opgave 3.1 3,87 0,152 641, 2 Bereken met behulp van Maxima: 2,13 7,29 78 0,62 45 (%i1) 3.87*0.152*641.2/(2.13*7.29*78*0.62*45);
II.3 Equivalentierelaties en quotiënten
 II.3 Equivalentierelaties en quotiënten Een belangrijk begrip in de wiskunde is het begrip relatie. Een relatie op een verzameling is een verband tussen twee elementen uit die verzameling waarbij de volgorde
II.3 Equivalentierelaties en quotiënten Een belangrijk begrip in de wiskunde is het begrip relatie. Een relatie op een verzameling is een verband tussen twee elementen uit die verzameling waarbij de volgorde
Verzameling die door PlotPar maar niet door PlotZer geplot kan worden:
 Oplossingen It s a plot! Verzameling die door PlotZer maar niet door PlotPar geplot kan worden: Merk op dat elke niet-constante veelterm willekeurig grote (absolute) waarden bereikt De enige begrensde
Oplossingen It s a plot! Verzameling die door PlotZer maar niet door PlotPar geplot kan worden: Merk op dat elke niet-constante veelterm willekeurig grote (absolute) waarden bereikt De enige begrensde
Heron driehoek. 1 Wat is een Heron driehoek? De naam Heron ( Heroon) is bekend van de formule
 Heron driehoek 1 Wat is een Heron driehoek? De naam Heron ( Heroon) is bekend van de formule = s(s a)(s b)(s c) met s = a + b + c 2 die gebruikt wordt om de oppervlakte van een driehoek te berekenen in
Heron driehoek 1 Wat is een Heron driehoek? De naam Heron ( Heroon) is bekend van de formule = s(s a)(s b)(s c) met s = a + b + c 2 die gebruikt wordt om de oppervlakte van een driehoek te berekenen in
Ringen en Galoistheorie, 1e deel, 19 april 2012
 Ringen en Galoistheorie, 1e deel, 19 april 2012 Bij dit tentamen mag het dictaat niet gebruikt worden. Schrijf op elk vel je naam, studnr en naam practicumleider. Laat bij elke opgave zien hoe je aan je
Ringen en Galoistheorie, 1e deel, 19 april 2012 Bij dit tentamen mag het dictaat niet gebruikt worden. Schrijf op elk vel je naam, studnr en naam practicumleider. Laat bij elke opgave zien hoe je aan je
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45](/thumbs/98/136422869.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
De partitieformule van Euler
 De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
RINGEN EN LICHAMEN. Aanvullende opgaven met uitwerkingen
 RINGEN EN LICHAMEN Aanvullende opgaven met uitwerkingen Hierna volgen een aantal aanvullende opgaven die gaan over kernbegrippen uit de eerste hoofdstukken van Ringen en Lichamen. Probeer deze opgaven
RINGEN EN LICHAMEN Aanvullende opgaven met uitwerkingen Hierna volgen een aantal aanvullende opgaven die gaan over kernbegrippen uit de eerste hoofdstukken van Ringen en Lichamen. Probeer deze opgaven
Grafieken van veeltermfuncties
 (HOOFDSTUK 43, uit College Mathematics, door Frank Ayres, Jr. and Philip A. Schmidt, Schaum s Series, McGraw-Hill, New York; dit is de voorbereiding voor een uit te geven Nederlandse vertaling). Grafieken
(HOOFDSTUK 43, uit College Mathematics, door Frank Ayres, Jr. and Philip A. Schmidt, Schaum s Series, McGraw-Hill, New York; dit is de voorbereiding voor een uit te geven Nederlandse vertaling). Grafieken
Enkele valkuilen om te vermijden
 Enkele valkuilen om te vermijden Dit document is bedoeld om per onderwerp enkele nuttige strategieën voor opgaven te geven. Ook wordt er op een aantal veelgemaakte fouten gewezen. Het is géén volledige
Enkele valkuilen om te vermijden Dit document is bedoeld om per onderwerp enkele nuttige strategieën voor opgaven te geven. Ook wordt er op een aantal veelgemaakte fouten gewezen. Het is géén volledige
Finaletraining Nederlandse Wiskunde Olympiade
 NEDERLANDSE W I S K U N D E OLYMPIADE Finaletraining Nederlandse Wiskunde Olympiade Met uitwerkingen Birgit van Dalen, Julian Lyczak, Quintijn Puite Dit trainingsmateriaal is deels gebaseerd op materiaal
NEDERLANDSE W I S K U N D E OLYMPIADE Finaletraining Nederlandse Wiskunde Olympiade Met uitwerkingen Birgit van Dalen, Julian Lyczak, Quintijn Puite Dit trainingsmateriaal is deels gebaseerd op materiaal
Opgaven Inleiding Analyse
 Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
1.1.2. Wiskundige taal. Symbolen om mee te rekenen + optelling - aftrekking. vermenigvuldiging : deling
 Examen Wiskunde: Hoofdstuk 1: Reële getallen: 1.1 Rationale getallen: 1.1.1 Soorten getallen. Een natuurlijk getal is het resultaat van een tellg van een edig aantal dgen. Een geheel getal is het verschil
Examen Wiskunde: Hoofdstuk 1: Reële getallen: 1.1 Rationale getallen: 1.1.1 Soorten getallen. Een natuurlijk getal is het resultaat van een tellg van een edig aantal dgen. Een geheel getal is het verschil
Geldwisselprobleem van Frobenius
 Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
1 Complexe getallen in de vorm a + bi
 Paragraaf in de vorm a + bi XX Complex getal Instap Los de vergelijkingen op. a x + = 7 d x + 4 = 3 b 2x = 5 e x 2 = 6 c x 2 = 3 f x 2 = - Welke vergelijkingen hebben een natuurlijk getal als oplossing?...
Paragraaf in de vorm a + bi XX Complex getal Instap Los de vergelijkingen op. a x + = 7 d x + 4 = 3 b 2x = 5 e x 2 = 6 c x 2 = 3 f x 2 = - Welke vergelijkingen hebben een natuurlijk getal als oplossing?...
Aanvullingen bij Hoofdstuk 8
 Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Oefenopgaven Grondslagen van de Wiskunde A
 Oefenopgaven Grondslagen van de Wiskunde A Jaap van Oosten 2007-2008 1 Kardinaliteiten Opgave 1.1. Bewijs, dat R N = R. Opgave 1.2. Laat Cont de verzameling continue functies R R zijn. a) Laat zien dat
Oefenopgaven Grondslagen van de Wiskunde A Jaap van Oosten 2007-2008 1 Kardinaliteiten Opgave 1.1. Bewijs, dat R N = R. Opgave 1.2. Laat Cont de verzameling continue functies R R zijn. a) Laat zien dat
Inleiding Analyse 2009
 Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Finaletraining Wiskunde Olympiade
 Finaletraining Wiskunde Olympiade Met uitwerkingen Birgit van Dalen, Julian Lyczak, Quintijn Puite, Merlijn Staps Voor het schrijven van dit trainingsmateriaal hebben we inspiratie opgedaan uit materiaal
Finaletraining Wiskunde Olympiade Met uitwerkingen Birgit van Dalen, Julian Lyczak, Quintijn Puite, Merlijn Staps Voor het schrijven van dit trainingsmateriaal hebben we inspiratie opgedaan uit materiaal
Combinatoriek groep 1 & 2: Recursie
 Combinatoriek groep 1 & : Recursie Trainingsweek juni 008 Inleiding Bij een recursieve definitie van een rij wordt elke volgende term berekend uit de vorige. Een voorbeeld van zo n recursieve definitie
Combinatoriek groep 1 & : Recursie Trainingsweek juni 008 Inleiding Bij een recursieve definitie van een rij wordt elke volgende term berekend uit de vorige. Een voorbeeld van zo n recursieve definitie
Aanvulling aansluitingscursus wiskunde. A.C.M. Ran
 Aanvulling aansluitingscursus wiskunde A.C.M. Ran 1 In dit dictaat worden twee onderwerpen behandeld die niet in het boek voor de Aansluitingscursus staan. Die onderwerpen zijn: complexe getallen en volledige
Aanvulling aansluitingscursus wiskunde A.C.M. Ran 1 In dit dictaat worden twee onderwerpen behandeld die niet in het boek voor de Aansluitingscursus staan. Die onderwerpen zijn: complexe getallen en volledige
boek Getallen 2009, errata (8 oktober 2011)
 boek Getallen 009, errata (8 oktober 0) De toren van Hanoi 6 0 van a naar b } van a naar b }. 8 6 en x / B } en x / B }. - zonodig zo nodig De natuurlijke getallen 3 - vermenigvuldigeing vermenigvuldiging
boek Getallen 009, errata (8 oktober 0) De toren van Hanoi 6 0 van a naar b } van a naar b }. 8 6 en x / B } en x / B }. - zonodig zo nodig De natuurlijke getallen 3 - vermenigvuldigeing vermenigvuldiging
Tentamen Grondslagen van de Wiskunde A Met beknopte uitwerking
 Tentamen Grondslagen van de Wiskunde A Met beknopte uitwerking 10 december 2013, 09:30 12:30 Dit tentamen bevat 5 opgaven; zie ook de ommezijde. Alle opgaven tellen even zwaar (10 punten); je cijfer is
Tentamen Grondslagen van de Wiskunde A Met beknopte uitwerking 10 december 2013, 09:30 12:30 Dit tentamen bevat 5 opgaven; zie ook de ommezijde. Alle opgaven tellen even zwaar (10 punten); je cijfer is
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 22 februari 2009 INDUCTIE & RECURSIE Paragrafen 4.3-4.6 Discrete Structuren Week 3:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 22 februari 2009 INDUCTIE & RECURSIE Paragrafen 4.3-4.6 Discrete Structuren Week 3:
1E HUISWERKOPDRACHT CONTINUE WISKUNDE
 E HUISWERKOPDRACHT CONTINUE WISKUNDE Uiterste inleverdatum dinsdag oktober, voor het begin van het college N.B. Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je moet het huiswerk
E HUISWERKOPDRACHT CONTINUE WISKUNDE Uiterste inleverdatum dinsdag oktober, voor het begin van het college N.B. Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je moet het huiswerk
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 2008 Limieten en asymptoten van rationale functies (versie juli 2008) Rationale functies. Inleiding Functies als f : 5 5, f 2 : 2 3 + 2 f 3 : 32 + 7 4 en f 4 :
Katholieke Universiteit Leuven September 2008 Limieten en asymptoten van rationale functies (versie juli 2008) Rationale functies. Inleiding Functies als f : 5 5, f 2 : 2 3 + 2 f 3 : 32 + 7 4 en f 4 :
Discrete Wiskunde, College 7. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 7 Han Hoogeveen, Utrecht University Sommatiefactor methode (niet in boek) Doel: oplossen van RBs als Basisidee: f n a n = g n a n 1 + c n ; 1 Vermenigvuldig de RB met een factor
Discrete Wiskunde, College 7 Han Hoogeveen, Utrecht University Sommatiefactor methode (niet in boek) Doel: oplossen van RBs als Basisidee: f n a n = g n a n 1 + c n ; 1 Vermenigvuldig de RB met een factor
In dit college bekijken we een aantal technieken om integralen te bepalen van trigonometrische functies en van rationale functies.
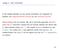 03 college 5: meer technieken In dit college bekijken we een aantal technieken om integralen te bepalen van trigonometrische functies en van rationale functies. Opmerking over de notatie. Net als in het
03 college 5: meer technieken In dit college bekijken we een aantal technieken om integralen te bepalen van trigonometrische functies en van rationale functies. Opmerking over de notatie. Net als in het
Selectietoets vrijdag 9 maart 2018
 Selectietoets vrijdag 9 maart 2018 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal
Selectietoets vrijdag 9 maart 2018 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal
2. Ga voor volgende relaties na of het al dan niet functies, afbeeldingen, bijecties, injecties, surjecties zijn :
 HOOFDSTUK. VERZAMELINGEN, RELATIES EN FUNCTIES Opgaven verzamelingen, relaties en functies. Toon aan : a) (A B) C = A (B C) b) A (B C) = (A B) (A C) c) (A B) c = A c B c d) A B B c A c. Ga voor volgende
HOOFDSTUK. VERZAMELINGEN, RELATIES EN FUNCTIES Opgaven verzamelingen, relaties en functies. Toon aan : a) (A B) C = A (B C) b) A (B C) = (A B) (A C) c) (A B) c = A c B c d) A B B c A c. Ga voor volgende
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: veeltermfuncties en berekening parameters, stelsels. 16 september dr.
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: veeltermfuncties en berekening parameters, stelsels 16 september 2017 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating)
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: veeltermfuncties en berekening parameters, stelsels 16 september 2017 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating)
Overzicht Fourier-theorie
 B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
PRIJEN en PRIPRIJEN Werkblad Rationale rechthoekige driehoeken
 PRIJEN en PRIPRIJEN Werkblad Rationale rechthoekige driehoeken Vooraf De vragen en opdrachten in dit werkblad die vooraf gegaan worden door, moeten schriftelijk worden beantwoord. Daarbij moet altijd duidelijk
PRIJEN en PRIPRIJEN Werkblad Rationale rechthoekige driehoeken Vooraf De vragen en opdrachten in dit werkblad die vooraf gegaan worden door, moeten schriftelijk worden beantwoord. Daarbij moet altijd duidelijk
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45](/thumbs/72/68043516.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
Week 22: De macht van het spoor en het spoor van de macht
 Week 22: De macht van het spoor en het spoor van de macht Een belangrijke invariant van een lineaire afbeelding is het spoor. Als we een basis kiezen dan is het spoor simpelweg de som van de elementen
Week 22: De macht van het spoor en het spoor van de macht Een belangrijke invariant van een lineaire afbeelding is het spoor. Als we een basis kiezen dan is het spoor simpelweg de som van de elementen
IMO-selectietoets III zaterdag 4 juni 2016
 IMO-selectietoets III zaterdag 4 juni 2016 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een natuurlijk getal. In een dorp wonen n jongens en n meisjes. Voor het jaarlijkse bal moeten
IMO-selectietoets III zaterdag 4 juni 2016 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een natuurlijk getal. In een dorp wonen n jongens en n meisjes. Voor het jaarlijkse bal moeten
Het karakteristieke polynoom
 Hoofdstuk 6 Het karakteristieke polynoom We herhalen eerst kort de definities van eigenwaarde en eigenvector, nu in een algemene vectorruimte Definitie 6 Een eigenvector voor een lineaire transformatie
Hoofdstuk 6 Het karakteristieke polynoom We herhalen eerst kort de definities van eigenwaarde en eigenvector, nu in een algemene vectorruimte Definitie 6 Een eigenvector voor een lineaire transformatie
2.0 Voorkennis. Rekenregels machten: 5) a 0 = 1. p p q p q a p q q. p q pq p p p. Willem-Jan van der Zanden
 2.0 Voorkennis Voorbeeld: (a + b) 2 = a 2 + 2ab + b 2 (a + b) 3 = (a +b)(a2 + 2ab + b2) = a 3 + 2a 2 b + ab 2 + a 2 b +2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 Rekenregels machten: p p q pq a pq 1) a a
2.0 Voorkennis Voorbeeld: (a + b) 2 = a 2 + 2ab + b 2 (a + b) 3 = (a +b)(a2 + 2ab + b2) = a 3 + 2a 2 b + ab 2 + a 2 b +2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 Rekenregels machten: p p q pq a pq 1) a a
