Monte-Carlo simulatie van verkeersafwikkeling op kruispunten
|
|
|
- Anneleen Beckers
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Katholieke Universiteit Leuven Faculteit Toegepaste Wetenschappen Departement Burgerlijke Bouwkunde Monte-Carlo simulatie van verkeersafwikkeling op kruispunten E2006 Promotor: L.Immers Nathan Van Paesschen
2 Toelating tot bruikleen De auteur geeft de toelating deze eindverhandeling voor consultatie beschikbaar te stellen en delen ervan te kopiëren voor eigen gebruik. Elk ander gebruik valt onder de strikte beperkingen van het auteursrecht; in het bijzonder wordt er gewezen op de verplichting de bron uitdrukkelijk te vermelden bij het aanhalen van resultaten uit deze eindverhandeling Leuven, juni
3 K.U.Leuven Fakulteit Toegepaste Wetenschappen Akademiejaar: Departement: Burgerlijke Bouwkunde Adres en tel.: Kasteelpark Arenberg Heverlee - 016/ Naam en voornaam student: Van Paesschen Nathan Titel eindwerk: Monte-Carlo simulatie van verkeersafwikkeling op kruispunten Korte inhoud Eindwerk: Bestaande analytische verkeersmodellen houden bij het berekenen van capaciteiten van kruispunten geen rekening met de interacties en conflicten tussen de verschillende verkeersstromen op het kruispuntvlak. In deze thesis wordt nagegaan wat de invloed van deze interacties is op de capaciteit van een kruispunt. Hiertoe wordt er een computermodel ontwikkeld dat er specifiek op gericht is om deze interacties en hun invloed op de verkeersafwikkeling te modelleren. Deze zaken werden in de bestaande literatuur nog maar weinig bestudeerd. Het onderzoek toont aan dat bij geringe drukte, het aantal interacties tussen de verschillende stromen klein is. Hun invloed op de verkeersafwikkeling blijft zeer beperkt. Het onderzoek toont verder aan dat bij toenemende drukte, het aantal interacties echter zo sterk kan toenemen dat er zich zelfs een capaciteitsval van het kruispunt kan voordoen. Bij grote belastingsgraden blijken de huidige verkeersmodellen, die geen rekening houden met deze interacties, de capaciteit van een kruispunt vaak substantieel te overschatten. Promotor: prof. L. Immers Assessoren: prof. E. Peetermans dr. C. Tampère 3
4 K.U.Leuven Fakulteit Toegepaste Wetenschappen year: Department: Burgerlijke Bouwkunde Address and tel.: Kasteelpark Arenberg Heverlee - 016/ Name and surname student: Van Paesschen Nathan Title of thesis: Analysing chaos on intersections using Monte-Carlo simulation techniques Summary of thesis: When calculating the capacity of junctions, current analytical traffic models don t take the interactions and conflicts between the different traffic flows on these junctions into account. As its main objective, this thesis analysed the influence of these interactions and conflicts on the total capacity of a junction. With the help of a self-created computer model, particularly focussed on the specific needs to model the interactions between traffic flows, the influence of conflicts between these flows on the capacity of junctions was studied. In the existing literature, this topic has almost never been studied. At low degrees of saturation, this influence turns out to be little. With increasing traffic however, the number of conflicts increases as well. The results of the research show that conflicts between the different traffic flows do not only have a limitation effect on the capacity of intersections. In some circumstances, they could even be the source of a capacity drop on the junction. In these situations, existing traffic models often overestimate the capacity of junctions. Estimations that at times can be too big to just ignore Promotor: prof. L. Immers Assessors: prof. E. Peetermans dr. C. Tampère 4
5 Dankwoord Vooreerst wil ik mijn promotor, professor Immers bedanken. Hij gaf me, als een student van de optierichting gebouwentechnieken, toch de mogelijkheid om mijn eindwerk bij de afdeling verkeer en infrastructuur te schrijven. Hierdoor kreeg ik de mogelijkheid mijn thesis te schrijven over een enorm boeiend onderwerp. Ook wil ik Eddy Peetermans bedanken voor het feit dat hij wilde inspringen als tweede assessor van deze thesis. In het bijzonder wil ik ook Chris Tampère heel erg bedanken. Als mijn personal coach wist hij me met zijn enthousiamse, inzicht en gedrevenheid enorm te motiveren. Zonder zijn inbreng zou deze thesis niet dezelfde zijn geweest. 5
6 6
7 0 Inleiding 10 1 Literatuurstudie Inleiding Traditionele verkeerstheorie Capaciteiten en de kritische parameters Vertraging Nieuwe ontwikkelingen en methodes methode van de conflictstromen Verkeersstromen als wachtrijen Besluit literatuurstudie 21 2 Modeldefinitie Afwikkelingsbepalende elementen Verkeerslichten Voorrangsregels Interacties tussen voertuigen onderling Interacties binnen 1 stroom Interacties tussen verschillende stromen Interacties tussen verschillende kruispuntvlakken Eigenschappen van voertuigen in de verkeersstromen Toevoer en afvoer van wagens Gap-acceptatie en follow-up time Aspecten met kleinere prioriteit Voetgangers Vertraging door het wisselen van rijstrook Knipperlichten Headway compressie Dynamische verkeerslichtenregeling 31 3 Conceptuele uitwerking van het model Het Black Box Concept Eigenschappen van de verschillende black boxes Het algemene karakter van de black boxes Het specifieke karakter van black boxes Verkeerslichten Capaciteit Interacties tussen de verschillende wachtrijen Toelevering op-1-toelevering op-m-toelevering Hinder en vermindering Voorrang en gap-acceptatie Omzetten van werkelijkheid naar model Definiëren van de wachtrijen Level-1-rijen Level-2-rijen 45 7
8 Level-3-rijen Nummering Aangeven van interacties Tel- en tijdmatrices Labelsysteem Beperkingen in modellering 51 4 Verificatie Wachtrijen als Markov-rijen M/M/ De kans op populatie k Gemiddeld aantal wachtenden De tijd gespendeerd in het systeem Besluit M/M/ Andere Markov-processen Besluit simulatie van Markov-processen Verkeerskundige processen Interactie tussen twee stromen aan kruispunten zonder verkeerslichten Capaciteit Vertraging Vertragingen berekend met tijdsonafhanlijke formules Formules berekend met tijdsafhankelijke berekeningen Vertragingen aan kruispunten met verkeerslichten Besluit verificatie 77 5 Hoofdstuk Toepassing Situatieschets Verschillende verkeersstromen Verkeerslichtenregeling Invloed van de verschillende stromen op elkaar Berekeningen en resultaten Verwaarlozen van de interacties Inrekenen van interacties tussen stromen Eerste orde hinder Eerste en tweede orde hinder Vertragingen Invloed van karakteristieke parameters op de capaciteit van het kruispunt De invloed van de bedieningstijd Invloed van de hinderlengte Conclusie Besluit Literatuuropgave 111 Afkortingenlijst 115 Lijst met figuren 116 Lijst met tabellen 117 8
9 Bijlage A: Werking van de simulatie 119 Bijlage B: Andere Markov-rijen 139 Bijlage C: Eigenschappen van de wachtrijen in de toepassing 148 Bijlage D: Intensiteiten en standaarddeviaties bij de toepassing 151 9
10 0 Inleiding De impact van het verkeer op onze maatschappij wordt steeds groter. Dagelijks halen verkeersopstoppingen het nieuws, en overal hoor je mensen klagen over de tijd die ze verliezen tijdens de dagelijkse rit naar en van het werk. Een vlottere verkeersdoorstroming zou voor vele pendelaars de werkdag heel wat aangenamer maken. Ook de mensen die hun rustige straatje elke dag weer omgetoverd zien tot een drukke sluipweg zijn deze verkeersoverlast liever kwijt dan rijk. De vaak stroef verlopende verkeerstromen hebben niet alleen sociale gevolgen, ook de economische gevolgen zijn enorm. Dagelijks worden er miljoenen euro s aan arbeidsuren verspild met wachten in de file. Enorme wachtrijen aan kruispunten zijn een economische ramp voor een stad. De middenstand in moeilijk bereikbare stadskernen, zoals Mortsel, ziet al jaren haar omzet achteruit gaan. Ook het milieu kreunt onder de impact van al de motoren die in de file staan te draaien en ondertussen tonnen CO 2 en andere schadelijke gassen de lucht insturen. De vraag vanuit maatschappij naar oplossingen klinkt steeds luider. Wanneer de verkeersafwikkeling over een verkeersnetwerk gesimuleerd wordt, dan wordt er voor de capaciteit van kruispunten vaak met arbitraire aannames gewerkt. De detailleringsgraad van macroscopische modellen is vaak niet fijn genoeg om de verkeersafwikkeling op kruispunten op een verfijnde manier weer te geven. Bovendien blijkt uit studie van de bestaande literatuur dat er over de impact van de interacties tussen verschillende stromen op een kruispuntvlak, op de capaciteit van dit kruispunt, bijna geen publicaties bestaan. Bestaande verkeersmodellen stellen de capaciteit van een kruispunt op op basis van de intensiteit van de verschillende wegen die aan het kruispunt toekomen. Bij stijgende verkeersvraag stijgt de intensiteit over het kruispunt, om uiteindelijk begrensd te worden door de maximale capaciteit van het kruispunt. Wat er op het kruispuntvlak zelf gebeurt, laten deze modellen buiten beschouwing. Zeker bij hogere saturatiegraden schieten deze modellen tekort in hun benadering van de werkelijkheid. Deze thesis heeft als doel na te gaan of interacties en conflicten tussen stromen op een kruispuntvlak weldegelijk een invloed hebben op de capaciteit van een kruispunt. Ze wil geen afgewerkt geheel zijn, maar eerder een aanleiding tot verder onderzoek onder de vorm van (post)doctoraatstudie. 10
11 In deze thesis is een computermodel opgesteld dat er precies op gericht is om de interacties tussen de verschillende stromen op het kruispuntvlak te modelleren. Na de bespreking van de literatuurstudie wordt uiteengezet wat de precieze vereisten voor het simulatiemodel zijn. Deze vereisten zijn er vooral op gericht om met het simulatiemodel een toegevoegde waarde te kunnen bieden ten opzichte van de bestaande onderzoeken en verkeersmodellen. De simulatie is op een zodanige wijze geconcipieerd dat ze later nog kan dienen voor verder en dieper onderzoek in navolging van deze thesis. Vanuit dit oogpunt is er dan ook uitgebreide zorg besteed aan de verificatie van de resultaten van het computermodel. Uit deze verificatie blijkt dat de simulaties de bekende formules en modellen, gelet op de aannames en vereenvoudigingen die deze maken, zeer goed benaderen. Het laatste hoofdstuk gaat aan de bestaande theorie voorbij. Er wordt met behulp van het simulatiemodel een verkeerssituatie uitgewerkt. Door deze simulatie uit te voeren met en zonder inrekenen van de interacties tussen stromen op het kruispuntvlak wordt nagegaan welke fout de bestaande verkeersmodellen maken door deze interacties te verwaarlozen. Deze fout blijkt in bepaalde omstandigheden zeer aanzienlijk te zijn. Bij stijgende verkeersbelasting ontstaan er tussen de verschillende stromen op het kruispunt meer en meer conflictsituaties. Er wordt aangetoond dat bij stijgende verkeersvraag de intensiteit van het kruispunt niet altijd naar een bovengrens convergeert. Integendeel! Net door dit toenemende aantal conflicten tussen de verschillende verkeersstromen kan vanaf een bepaald punt de capaciteit van het kruispunt afnemen bij stijgende verkeersvraag. Er doet zich een capaciteitsval voor. Uiteindelijk wordt er nog kort even ingegaan op enkele parameters die de aard van deze capaciteitsval beïnvloeden. Welke al deze parameters zijn, en waar hun precieze invloed op de capaciteit van het kruispunt zich precies situeert, paste niet meer in het bestek van deze thesis. De thesis probeert een lans te breken voor dieper en uitgebreider onderzoek naar de verkeersprocessen op het kruispuntvlak, en hun invloed op de capaciteit van het kruispunt en het volledige netwerk. Enkel indien een goed inzicht verworven wordt in deze processen zullen goede en betrouwbare voorspellingen kunnen gedaan worden in verband met de prestaties van kruispunten, en van het hele netwerk 11
12 1 Literatuurstudie 1.1 Inleiding In deze thesis wordt bestudeerd welke de invloed is van de interacties tussen verkeersstromen op de verkeersafwikkeling op en rond het kruispuntvlak. Bij verschillende belastingsgraden zullen vertragingen, gemiddelde wachtrijlengtes en de capaciteit van kruispunten als belangrijkste parameters voor deze verkeersafwikkeling met elkaar vergeleken worden. Hiertoe wordt een simulatiemodel geprogrammeerd. Om een inzicht te krijgen in de verkeersprocessen die geprogrammeerd dienen te worden wordt eerst een studie van de literatuur in verband met deze processen en interacties gemaakt. Bovendien worden, na het programmeren, de resultaten uit het simulatiemodel gestaafd worden met de analytische en deterministische formuleringen die worden teruggevonden in de literatuur. Voor wetenschappelijke publicaties daterend van voor 1999 hebben we ons gebaseerd op een samenvatting van de meest relevante werken, gepubliceerd door de Transportation Research Board (TRB). Naast dit rapport werden ook de nieuwe onderzoeksprojecten en papers gepubliceerd tot en met 2005, die betrekking hebben op deze thesis, bestudeerd. Hiertoe hebben we ons laten leiden door de proceedings van het jaarlijkse congres van de TRB. In 1999 werd er door de TRB een rapport gepubliceerd [TRB]. Het is een door de TRB verbeterde versie van een monografie, product van een samenwerking tussen The Federal Highway Administration (FHWA) en het Oak Ridge National Laboratory, waarin alle belangrijke ontwikkelingen in de verkeerstheorie worden samengevat. In het rapport wordt dus zowel naar de grondleggers en de basisbeginselen van de verkeersstudie als naar meer gespecialiseerde werken verwezen. 12
13 Bij het bestuderen van de processen die zich voordoen bij de verkeersafwikkeling op kruispunten wordt er in de verkeerstheorie in de eerste plaats een onderscheid gemaakt tussen kruispunten met of zonder verkeerslichten. Er zijn verschillende goede redenen om deze scheiding te maken. Zo bijvoorbeeld hebben de stromen uit de verschillende richtingen op kruispunten met lichten beurtelings voorrang, waardoor er eerder naar dichotome 1 distributies moet gegrepen worden. Ook is de correlatie tussen de verschillende stromen op dit soort kruispunten minder groot. [Buckley (1968),Cowan (1975),Dawson (1969), Schuhl(1955)] Op kruispunten zonder verkeerslichten is er meestal 1 stroom die een continue voorrang geniet 2,waardoor vertrekprocessen andere distributies kennen. Het is duidelijk dat naast deze belangrijke verschillen er ook zeer grote overeenkomsten bestaan tussen intersecties met of zonder verkeerslichtenregeling. Binnen deze twee verschillende categorieën zijn formuleringen opgesteld voor de berekening van zowel de capaciteiten van, als de vertragingen op het kruispunt. Het berekenen van capaciteiten van een kruispunt met of zonder verkeerslichten gebeurt op verschillende manieren. Ook voor het berekenen van vertragingen worden verschillende methodes en formuleringen gebruikt voor deze twee soorten kruispunten. Naast deze opsplitsing kan de verkeerstheorie ook opgesplitst worden in een traditionele en een meer progressieve verkeerstheorie. Alle methodes die via rigoureuze wiskundige benaderingen tot formules proberen te komen worden als traditioneel geclassificeerd. Omdat het met analytische formules snel moeilijk wordt om nog tot een goede beschrijving te komen van complexere situaties zijn er de laatste jaren methodes ontstaan die niet meer vanuit pure wiskundige formuleringen vertrekken. Een belangrijke methode is de methode van de conflictstromen die ontwikkeld is door Werner Brilon en Ning Wu. In de rest van dit hoofdstuk worden de resultaten van beide werkwijzen meer in detail besproken. 1 Een dichotome verdeling is een combinatie van verschillende verdelingen. Ze veronderstelt dat een bepaald deel van de wagens in de stroom vrij en ongehinderd kan rijden in de stroom, en dat het andere deel van de voertuigen in groep rijdt. Een gekende dichotome verdeling is de M3 verdeling Cowan [Cowan, 1975] 2 Voorrangsbaan of voorrang van rechts 13
14 1.2 Traditionele verkeerstheorie Capaciteiten en de kritische parameters Onder capaciteit wordt de redelijk te verwachten maximum en onderhoudbare hoeveelheid verkeersstroom onder bepaalde en gegeven voorwaarden verstaan. Capaciteit beschrijft dus de gemiddelde (verwachte) maximale stroom die over een lange periode kan voldaan blijven. Dit is de definitie gegeven door de Highway Capacity Manual.[HCM 2000]. Bij de berekening van de capaciteiten maakt men gebruik van de gap acceptance theory. De gap acceptance theory bestudeert de fenomenen die verband houden met de distributie van wagens in een verkeersstroom. Twee van deze fenomenen met een bijzonder belang voor de studie van verkeersprocessen op kruispunten zijn de critical gap en follow-up time 3. Men noemt ze de kritische gap parameters. De kritische gap (gap= tussenruimte) is de minimale afstand die een bestuurder wil hebben tussen twee opeenvolgende wagens in een stroom die hij wil kruisen vooraleer hij deze stroom daadwerkelijk zal kruisen. De follow-up tijd is de tijd tussen twee opeenvolgende wagens die een verkeersstroom kruisen, wanneer ze gebruik maken van dezelfde gap. In de gap acceptance theory kunnen twee verschillende benaderingsmethodes onderscheiden worden. De empirische regressiemethode, waarbij men continue wachtrijen veronderstelt en de Gap Acceptance Procedures (GAP-methodes), waarbij men gebruik maakt van meer probabilistische methodes. [veronderstelling continue wachtrijen: Harders (1976), Siegloch (1973), Tanner (1962), Troutbeck (1986); meer probalistische methodes: Hewitt (1983), Miller (1972), Ramsey en Routledge (1973), Troutbeck (1975)] 3 Verder in de tekst zullen de respectievelijke termen kritische gap en follow-up tijd gebruikt worden. In formules worden de kritische gap en de follow-up tijd afgekort met de respectievelijke symbolen T c en T f 14
15 Het schatten van de kritische parameters is zeer ingewikkeld omdat men deze schattingen niet empirisch kan toetsen. Het is immers onbegonnen werk om verschillende wagens gedurende een periode te volgen om zo ieders kritische parameters op te meten. Bovendien hangen ze ook af van de typologie van het kruispunt zelf. Het schatten van deze parameters hangt zeer nauw samen met de studie naar de verdeling van de tussenafstanden tussen de verschillende wagens 4. Een eenvoudige veronderstelling stelt dat deze afstanden onafhankelijk van elkaar zijn. Een exponentiële verdeling is dan aangewezen. De afstand tussen verschillende auto s is echter groter dan een minimale waarde, waardoor een verschoven exponentiële verdeling zich opdringt. Om effecten zoals platooning 5 of groepsvorming correct in te rekenen worden vaak dichotome verdelingen gebruikt zoals het M3 model van Cowan of een hyper-erlang verdeling. [Brilon (1996), Catchpole en Planck (1986), Cowan (1975),Hewitt (1985), Tian(1999),Troutbeck(1988), Wegmann (In Brilon: 1991)] 4 In de Engelstalige literatuur noemt men deze tussenafstanden headways. 5 Platooning: Men spreekt over platooning wanneer auto s in een groep of peloton achter elkaar aanrijden. Dit fenomeen komt bvb. voor wanneer een eerste wagen trager rijdt als de volgende wagen, maar wanneer er niet voorbij gestoken kan worden. Ook nadat de verkeerslichten op groen zijn gesprongen en alle wagens in groep wegrijden kan men over platooning spreken. 15
16 1.2.2 Vertraging Vertraging of delay op kruispunten is één van de meest belangrijke parameters bij het evalueren van de prestaties van kruispunten. Een goed inzicht in de parameters die een invloed uitoefenen op de vertraging op kruispunten is bepalend voor een goede inrichting van het kruispunt. Wat men verstaat onder een goede inrichting en bijhorende verkeersafwikkeling is voor discussie vatbaar. Sommigen stellen dat de gemiddelde vertraging zo klein mogelijk moet zijn, terwijl anderen dan weer menen dat er ook een maximum wachttijd voor iedere gebruiker van het kruispunt in acht moet genomen worden om nog van een goede afwikkeling te kunnen spreken. De kwaliteit van de verkeersafwikkeling op een kruispunt kan gekarakteriseerd worden door de zogenaamde measures of effectiveness (MOE s, de maatstaven voor de effectiviteit van de verkeersafwikkeling ). De gemiddelde vertraging, de gemiddelde wachtrijlengte, de verdeling van de vertragingen, de verdeling van de wachtrijlengtes, het aantal voertuigen dat tot een stop is moeten komen en de waarschijnlijkheid op een lege wachtrij zijn de voornaamste MOE s. Een ander belangrijk verschil tussen de analytische beschrijvingsmethodes ligt in het feit of het beschreven proces als stationair dan wel als dynamisch 6 beschouwd wordt. Vele macroscopische formuleringen zijn maar bruikbaar binnen een beperkt domein wanneer men rekening houdt met de vereenvoudigde veronderstellingen van tijdsonafhankelijkheid. Zo vereist tijdsonafhankelijkheid op kruispunten met verkeerslichten dat de wachtrij na elke lichtcyclus weer leeg is. Analytische formuleringen die tijdsonafhankelijkheid veronderstellen zijn daarom maar praktisch bruikbaar in stationaire condities met constante verkeersvolumes en bij saturatiegraden tot 1. 6 Hoewel transient misschien een betere uitdrukking zou zijn wordt er in het verkeerskundig vakjargon steeds de term dynamisch gebruikt. 16
17 Tijdsafhankelijke benaderingen worden echter vlug analytisch zeer moeilijk oplosbaar. Kimber en Hollis publiceerden in 1979 een werk dat aan basis ligt van de dynamische analyse van kruispunten met behulp van wachtrijtheorie. Door gebruik te maken van de coördinaten transformatiemethode stellen ze tijdsafhankelijke formuleringen op voor de vertragingen en wachtrijlengtes aan kruispunten. [vertragingen, geen verkeerslichten, tijdsonafhankelijk: Adams (1936), Cowan (1987), Daganzo (1977), Harders (1968), Kremser (1964), Tanner (1962), Troutbeck (1990); wel signalisatie:miller (1963), Newell (1965), Webster(1958)] [vertraging, geen verkeerslichten, tijdsafhankelijk: Newell (1982),Akçelik (1991)] [vertraging, wel verkeerslichten,tijdsafhankelijk: Akçelik en Rouphail (1994), Kimber en Hollis (1979), Olszewski (1990)] Er werd een kort overzicht geschetst van de traditionele aanpak van de problemen die zich stellen. Voor een grondiger overzicht verwijzen we naar hoofdstuk 8 [unsignalized intersection theory, Troutbeck & Brilon] en hoofdstuk 9 [traffic flow at signalized intersections, Rouphail,Tarko & Li] van het hierboven reeds vermelde rapport van de TRB uit 1999 [TRB]. We kunnen besluiten dat traditionele verkeersmodellen geen rekening houden met bepaalde interacties tussen verkeersstromen. Bij hoge saturatiegraden nemen de interacties tussen stromen op het kruispuntvlak sterk toe, waardoor vertragingen hoog kunnen oplopen. Hier schieten de huidige modellen tekort. Ook wordt de invloed van kruispunten verder in de verkeersstroom niet beschouwd. De traditionele verkeerstheorie laat dus nog heel wat ruimte voor verder onderzoek naar vertragingen als gevolg van de interacties tussen stromen rond maar vooral ook op kruispunten. 17
18 1.3 Nieuwe ontwikkelingen en methodes Al snel duiken er problemen op wanneer men een verkeerssituatie met minder eenvoudige, of tijdsafhankelijke parameters wenst te beschrijven met de GAP-methodes. Een analytische formulering voor complexe kruispuntvlakken opstellen is een onbegonnen werk en het berekenen van praktisch bruikbare resultaten is derhalve onmogelijk methode van de conflictstromen Een methode die deze problemen op een relatief eenvoudige wijze aanpakt, is de methode van de conflictstromen. Aan de basis van deze methode ligt het concept van de additieve conflictstromen (ACF). Dit concept werd voor het eerst beschreven door Gleue (1972), om kruispunten met verkeerslichten te analyseren. Het concept van de conflictstromen werd in 2000 bijgeschaafd door Wu, en toegepast op allway-stop-controlled (AWSC) 7 intersecties. In 2001 werd hetzelfde concept toegepast op two-way-stop-controlled intersecties door Brilon en Wu. De paper Capacity and Delays at Intersections Without Traffic Signals door Werner Brilon en Thorsten Miltner, voorgesteld in de TRB 2005 bouwt het concept van de conflictstromen verder uit, en toont er de sterktes van deze werkwijze in aan. De methode van de conflictstromen definieert op het kruispunt een aantal conflictpunten en conflictzones. Dit zijn zones waar twee of meerdere stromen elkaar kruisen en elkaar kunnen hinderen. Op basis van de voorrangsregels tussen de verschillende stromen wordt een voorrangsnetwerk tussen de verschillende stromen opgesteld. Hiertoe krijgen de stromen een rang toebedeeld die hun onderlinge voorrangsverplichtingen aangeeft (hogere rang heeft voorrang). Het geheel van deze relaties wordt samengevat in een conflictmatrix. Deze is makkelijk uitbreidbaar zodat op een relatief eenvoudige wijze ook moeilijke verkeerssituaties geanalyseerd kunnen worden. Na het opstellen van deze conflictmatrix moeten ook de kansen dat de voertuigen met verschillende rang zich op het conflictpunt bevinden worden geschat. 7 Kruispunten waar voor alle wegen die aankomen aan dit kruispunt verkeerlichten voorzien zijn. 18
19 Door deze verschillende kansen te vermenigvuldigen met de maximale capaciteit die de voertuigen van een bepaalde rang kennen wanneer ze niet gehinderd worden, kunnen uiteindelijk uit de conflictmatrix de capaciteiten van de verschillende stromen berekend worden. De werkwijze is relatief eenvoudig, maar levert toch zeer goede resultaten op. Deze methode verschilt van de meer conventionele werkwijzes, in het feit dat ze vertrekt vanuit strikt wiskundige formules en benaderingen. In de verdere uitwerking van het simulatiemodel wordt ook gebruik gemaakt van een conflictmatrix. De simulatie verschilt van de conflictmethode in deze dat de waarschijnlijkheden op een aanwezigheid van de voertuigen niet expliciet geschat worden. Ze volgen impliciet uit de simulatie. Met de conflictmethode is het makkelijker om rekening te houden met het aantal rijstroken, de distributies van de verkeersstromen, de voetgangers die eigenlijk integraal deel uitmaken van de verkeersafwikkeling, en met de rijstroken waar het licht oranje staat te knipperen. Ook het inrekenen van gelimiteerde 8 en omgekeerde 9 voorrang stelt geen grote problemen voor de conflictmethode. De conflicttechniek schuift een alternatief naar voor om de capaciteit van de verschillende bewegingen op het kruispunt te berekenen. Het afleiden en berekenen van andere prestatieparameters zoals de vertragingen, de wachtrijlengtes en lane sharing 10 gebeurt op de conventionele wijze. 8 Gelimiteerde voorrang: Wanneer een voertuig een verkeersstroom kruist of er in invoegt, kan het voorkomen dat een wagen in deze stroom dient af te remmen om botsingen te vermijden. Hierdoor wordt zijn voorrang gelimiteerd. 9 Omgekeerde voorrang: Dit fenomeen doet zich voor wanneer een chauffeur die voorrang heeft zijn voorrang afstaat aan een automobilist die volgens de verkeersregels voorrang zou moeten geven. De voorrang wordt daarmee omgekeerd. 10 Onder lane sharing verstaat men het delen van 1 rij- of opstelstrook door wagens die een verschillende richting uitmoeten. Een gekend effect hiervan doet zich voor wanneer wagens die linksaf of rechtdoor moeten een opstelstrook delen. De wagens die rechtdoor moeten kunnen gehinderd worden door de wagens die linksaf moeten omdat deze nog gehinderd worden door een stroom uit de tegenovergestelde richting 19
20 1.4 Verkeersstromen als wachtrijen In de simulatie wordt het kruispunt beschouwd als een aaneenschakeling van wachtrijen. Eens het kruispuntvlak op een effectieve wijze ontrafeld is tot een aantal samenhangende wachtrijen is het belangrijk om ook op een juiste wijze eigenschappen toe te kennen aan deze rijen. In de simulatie worden de wachtrijen gebaseerd op Markov-rijen, en meer bepaald op geboorte- en sterfteprocessen (GS-proces). Een wachtrij wordt gekenmerkt door een populatie, het aantal auto s in de wachtrij. Bij deze GS-processen kan er vanuit deze toestand enkel over gegaan worden in een populatie die 1 wagen groter of kleiner is. In hoofdstuk 4 wordt hierop verder ingegaan. Correcte resultaten vereisen een realistische benadering van de wachtrijmodellen. Als de saturatiegraad van een kruispunt dicht bij 1 ligt, of zelfs groter als 1 is, of wanneer de initiele wachtrij niet leeg is,dan heeft de wachtrij een dynamisch karakter. In 2004 stelden Viti en Van Zuylen een Markov-model voor dat ontworpen is om juist deze dynamische eigenschappen van de wachtrijen te berekenen. De nieuwe formuleringen zijn een uitbreiding van de reeds bestaande wiskundige benaderingen voor rijlengtes door Akçelik (die geen rekening houdt met initiele wachtrijen die niet leeg zijn) en Catling. In hun werk bespreken Viti en Van Zuylen het belang van enkele wiskundige parameters zoals de standaarddeviatie op de verwachtingswaarde en de evolutie van wachtrijen. Elke studie rondom verkeersafwikkeling heeft wel van dichtbij of veraf te maken met wachtrijen. Daarom zou het onbegonnen werk zijn om hier een uitputtende lijst van werken op te sommen. Enkele andere interessante werken zijn van de hand van Abu-Lebdeh en Benekohal (1997), Akçelik(1993), Banks en Amin(2003), Kimber en Hollis(1979) en Wu (2004). Niet alleen de interacties die verkeersstromen met elkaar aangaan op het kruispuntvlak bepalen de vertragingen die wagens kunnen oplopen aan een kruispunt. Soms kan de storende invloed van verderop in het netwerk komen. Ahmed en Abu-Lebdeh (2005) bestudeerden de vertragingen geïnduceerd door verstoringen verderop in het verkeersnetwerk. Deze verstoringen worden door de huidige modellen verwaarloosd. Uit de paper blijkt dat, zeker in situaties met zware belasting, deze vertragingen toch significant kunnen zijn en het is dus belangrijk om hier bij het opstellen van een simulatiemodel rekening mee te houden. 20
21 1.5 Besluit literatuurstudie Uit de literatuurstudie komt duidelijk naar voor dat er al grondig onderzoek verricht is naar vertragingen voor verkeersstromen aan kruispunten. Aankomst- en vertrekprocessen werden al uitvoerig onder de loep genomen en ook tal van andere aspecten zoals gelimiteerde voorrang, lane sharing, headway compressie 11, de invloed van afslagmanoeuvres, vormden reeds het onderwerp van menig wetenschappelijk onderzoek. Met de conflictmethode worden de interacties van stromen op een kruispuntvlak bestudeerd. Toch is de invloed van deze interacties op de vertragingen en op de capaciteit van het kruispunt nog steeds te weinig onderzocht en beschreven. Vooral kruispunten die rond het verzadigingspunt belast worden, bieden nog voldoende stof voor verder en meer diepgaand wetenschappelijk onderzoek. Zo zijn de effecten van een overgang van een onder- naar oververzadiging van een kruispunt nog nauwelijks bestudeerd. Analytische formules veronderstellen dat, wanneer de saturatiegraad van een kruispunt naar 1 gaat, dan de gemiddelde vertragingen oneindig groot worden en dat er bij saturatiegraden groter dan 1 zelfs helemaal geen verkeersstroming is. Dit is niet juist. Empirische metingen tonen aan dat ook bij saturatiegraden groter dan 1 er verkeersstroming blijft, al zullen de gemiddelde vertragingen wel toenemen. In macroscopische modellen wordt er meestal een maximale capaciteit verondersteld die constant blijft bij overcapaciteit. Ook dit is niet waar. Bij zeer grote belastingen neemt de maximale capaciteit af, en dit door een toegenomen aantal interacties tussen verkeersstromen. In deze thesis wordt er een verkeerssimulatie worden waarmee interacties tussen verkeersstromen op en rond het kruispunt gesimuleerd kunnen worden. Met deze simulatie kan hun invloed op de vertragingen en de capaciteiten van een kruispunt worden bestudeerd. Ook zullen de interacties tussen verschillende kruispunten nagegaan worden. Met de simulatie zal ook nagegaan worden wat de invloed is van parameters zoals de saturatiegraad op de vertraging, de capaciteit en de wachtrijlengtes. Er wordt immers vermoed dat vanaf bepaalde saturatiegraden de interacties tussen stromen zo groot worden dat het verkeer op kruispunten bijna stil komt te staan. 11 Headway compressie: De afstand tussen twee wagens in een verkeersstroom wordt in het engels een headway genoemd. Wanneer nu auto s achter elkaar een wachtrij uitrijden wordt de afstand die de opeenvolgende wagens tussenlaten kleiner en kleiner. Dit effect wordt in de literatuur headway compressie geheten. 21
22 In deze situaties zijn het niet langer de offset-tijden tussen verschillende verkeerslichten, de vertrekpatronen of de cycluslengtes die de vertragingen bepalen, zoals de huidige literatuur laat uitschijnen. De hinder die de verschillende verkeersstromen op elkaar uitoefenen worden dan bepalend. Bij welke saturatiegraden er een daling in capaciteit en toegenomen vertragingen optreden, en of dit eerder een bruusk dan wel een effect met een duidelijke overgangsfase is wordt ook nagegaan. Uiteindelijk wordt een besluit getrokken waarin de invloed van interacties tussen stromen op de capaciteit en de vertragingen wordt geëvalueerd.. 22
23 2 Modeldefinitie Vooraleer verder wordt ingegaan op de uitwerking van de computersimulatie worden in dit hoofdstuk eerst de verschillende aspecten van de verkeersafwikkeling die men er mee wenst te simuleren besproken. In dit hoofdstuk worden dus de functionele vereisten van het model uiteengezet. Alle fenomenen die in dit hoofdstuk worden besproken, moeten gemodelleerd kunnen worden. Er wordt ook aangegeven welke vereenvoudigingen en aannames er gemaakt worden. 2.1 Afwikkelingsbepalende elementen Verkeerslichten Eén van de meest bepalende elementen voor een goede verkeersafwikkeling is het verkeerslicht. Door het plaatsen van verkeerslichten nemen de interacties tussen verschillende stromen op het kruispuntvlak af. Met het verkeerslicht wordt een systeem van wisselende voorrang ingevoerd. Hierbij hebben de lengtes van de groen- en roodfase, de cycluslengte en de afstemming van verschillende verkeerslichten op elkaar, een grote invloed op de vertragingen die automobilisten oplopen op kruispunten. In het model kunnen deze lengtes worden aangepast, en kunnen verschillende verkeerslichten op elkaar worden afgestemd. Zo kan bij een simulatie van een kruispunt kunnen worden nagegaan wat de invloed is van bvb. verschillende cycluslengtes op de gemiddelde wachtrijlengtes. Ondanks het feit dat interacties tussen stromen afnemen dankzij het plaatsen van verkeerslichten, is dit geen garantie voor het uitblijven deze interacties. Voorbeelden uit de praktijk zijn hierbij legio. Zeker bij een grote belasting gebeurt het dat het kruispunt vol wagens staat die elkaar allen verhinderen het kruispuntvlak op of af te rijden. Het zou zelfs kunnen zijn dat net door de aanwezigheid van verkeerslichten de vertragingen toenemen 12. Het is dan ook verkeerd, zeker in de drukke en kritische spitsperiodes, om voor de capaciteit van een kruispunt zomaar te rekenen met de capaciteit die men zou hebben indien vrije uitstroom gegarandeerd is. 12 Wanneer een bestuurder groen licht heeft rijdt hij het kruispuntvlak op. Het maakt hem daarbij niet uit of hij met deze beweging andere stromen zou kunnen hinderen omdat hij het kruispuntvlak niet afgeraakt. Hierdoor kan het kruispunt klem komen te zitten en kunnen er grote vertragingen optreden. 23
24 Het model kan gebruikt worden om een beeld te vormen van de overschatting van de capaciteit indien men dit toch doet. Er wordt verondersteld dat alle chauffeurs zich aan de verkeerslichten houden. Er wordt geen rekening gehouden met de invloed van automobilisten die het rood licht negeren en geen rekening houden met de verkeersregels Voorrangsregels In de simulatie kunnen voorrangsregels worden ingebouwd. Hierbij wordt dan gedacht aan voorrang van rechts of de voorrang van wagens die op een voorrangsweg rijden. Het model gaat er vanuit dat iedereen zich aan deze regels houdt en zijn voorrang daadwerkelijk geeft, maar ook neemt. Fenomenen zoals omgekeerde voorrang, waarbij een chauffeur zijn voorrang afstaat, of gelimiteerde voorrang, waarbij een automobilist op een voorrangsweg moet afremmen omdat een andere wagen zijn baan kruist of er zich invoegt, zijn persoonsgebonden en moeilijk te modelleren. Met dit soort voorrang houdt het model geen rekening Interacties tussen voertuigen onderling In heel het verkeersproces gaan wagens continu interacties met elkaar aan. Elke beweging die een wagen maakt, zal andere wagens tot een reactie nopen. Het spectrum van deze interacties is zeer breed. Daarom worden verder in de tekst alleen deze interacties besproken die een invloed uitoefenen op de verkeersstromen op kruispunten, en die door het programma gesimuleerd kunnen worden. Deze interacties kunnen opgedeeld worden in drie categorieën, nl. interacties binnen 1 stroom, tussen verschillende stromen en interacties tussen verschillende kruispuntvlakken. Deze drie categorieën worden hieronder besproken. 24
25 Interacties binnen 1 stroom Een belangrijke soort interactie tussen wagens in één stroom ontstaat door het fenomeen van lane sharing. Bij lane sharing staan wagens die op het kruispunt verschillende richtingen uit moeten, opgesteld in dezelfde voorsorteerstrook. Ze delen dus deze opstelstrook met elkaar. Dit heeft tot gevolg dat, indien de eerste wagen in de wachtrij verhinderd wordt om het kruispuntvlak af te rijden, alle andere auto s genoodzaakt zijn ook te wachten, zelfs indien de richting die zij uit moeten helemaal niet geblokkeerd is. Een zeer gekend voorbeeld zijn auto s die linksaf wensen te slaan, maar gehinderd worden door auto s uit de tegenovergestelde richting. Hierdoor hinderen ze auto s die achter hen staan opgesteld en rechtdoor wensen te rijden. In het model kan gekozen worden of deze hinder al dan niet ingerekend wordt. Zo kan er vergeleken worden wat de werkelijke invloed is van lane sharing. Een andere vorm van interacties binnen één stroom vindt men terug in het fenomeen van platooning. Auto s rijden achter elkaar in een groepje of peloton. Dit komt bvb. voor op een plaats waar niet voorbij gestoken mag worden en wanneer de eerste wagen in een rij auto s relatief traag rijdt. Alle andere wagens zijn dan genoodzaakt zich aan het tempo van de eerste te houden en rijden zo in groep verder. Zoals in het hoofdstuk verificatie zal aangetoond worden, zijn de gemiddelde vertragingen ook functie van de distributies van de aankomst- en vertrekprocessen. Wanneer de wagens verondersteld worden onafhankelijk van elkaar aan te komen, kunnen hun aankomsten gemodelleerd worden met een exponentiële verdeling. Een andere distributie die vaak verondersteld wordt is de constante distributie. Andere verkeerssituaties worden dan weer best beschreven door andere verdelingen zoals een verschoven exponentiële verdeling, een Erlang-distributie van hogere orde of bepaalde dichtome verdelingen. Daarom is het nodig dat met het model ook deze verschillende distributies gemodelleerd kunnen worden, al zal blijken dat door het expliciet simuleren van de verkeersstromen de simulatie zelf tot analytisch moeilijk te beschrijven maar realistische distributies komt. 25
26 Interacties tussen verschillende stromen In omstandigheden met een beperkte verkeersvraag, waarin een normale verkeersafwikkeling mogelijk blijft, zorgen verkeerslichten er in principe voor dat verschillende verkeersstromen aan een kruispunt maar weinig interacties met elkaar hoeven aan te gaan. Een voorbeeld van een interactie die wel kan voorkomen, is het fenomeen dat hierboven reeds besproken werd, waar een stroom die linksaf wil slaan gehinderd wordt door een tegemoet komende verkeersstroom waaraan ze voorrang verschuldigd is. De stroom moet dan wachten tot ze ongehinderd het kruispuntvlak af kan rijden. Vaak is dit pas het geval wanneer de verkeerslichten al op rood zijn gesprongen. De wagens rijden het kruispuntvlak dus af tijdens de rood lichtfase. Dit fenomeen vindt men in de literatuur terug als red clearance, en de tijdsspanne waarin dit gebeurt heet men het red clearance interval. Bij zeer grote belastingen van het verkeersnetwerk, kan het voorkomen dat het red clearance interval van een stroom op het kruispuntvlak zo groot wordt bvb. doordat de wagens het kruispunt simpelweg niet meer af kunnen rijden- dat de voertuigen nog steeds op het kruispunt staan wanneer een stroom uit de andere richting weer groen heeft gekregen. Hierdoor neemt ook de afrijcapaciteit van deze stroom af. In het slechtste geval blijft een deel van deze nieuwe stroom op zijn beurt weer staan op het kruispuntvlak, waardoor de capaciteit van het kruispunt in een neerwaartse spiraal kan komen tot het hele kruispunt klem komt te staan. Wanneer er geen verkeerslichten voorzien zijn zorgen voorrangsborden en regels ervoor dat het verkeer zo vlot mogelijk verloopt. In deze situaties oefent de stroom die voorrang krijgt wel een invloed uit op de stroom die voorrang moet geven (de zijstroom). De wagens in de zijstroom dienen te wachten tot de tussenafstand tussen twee wagens in de hoofdstroom groot genoeg is, om deze zonder storen te kunnen kruisen of erin in te voegen. De capaciteit (wagens/uur) van de zijstroom zal dus mede bepaald worden door de verdeling van de tussenafstanden tussen voertuigen in de hoofdstroom, headways of gaps genaamd. Ook de aard van de chauffeurs in de zijstroom bepaalt voor een deel de maximale capaciteit van de zijstroom. 26
27 Zo moet men zich afvragen wat de minimum afstand, de kritische gap tussen twee auto s uit de hoofdstroom moet zijn vooraleer een auto uit de zijstroom deze hoofdstroom durft te kruisen. Indien een tussenruimte benut wordt door de automobilist spreekt men van gap-acceptatie. Ook de tussentijd die twee automobilisten laten wanneer die achter elkaar de hoofdstroom kruisen (follow-up time) speelt een niet te onderschatten rol Interacties tussen verschillende kruispuntvlakken Wanneer de wachtrij aan een kruispunt zo lang wordt, dat de staart van deze rij de auto s op een nabij gelegen kruispunt hindert van dit kruispunt af te rijden, dan spreekt men van spillback. Spillback is dus een fenomeen veroorzaakt door een stroomafwaarts gelegen kruispunt. Meer algemeen kan onder dit fenomeen elke wachtrij beschouwd worden die een andere verkeersstroom hindert doordat ze zo is uitgegroeid. Om rekening te kunnen houden met dit fenomeen, moeten in het model dus wegen of opstelstroken met een beperkte opstelcapaciteit gemodelleerd kunnen worden. Een kruispunt zorgt ook vaak voor een soort platooning effect. Dit effect komt voor wanneer auto s van het ene kruispunt naar het andere kruispunt rijden. Aan het eerste kruispunt worden de auto s voor het rode licht verzameld, waarna ze bij groen min of meer in groep tot het volgende kruispunt rijden. Het eigenlijke uitrijpatroon is zeer moeilijk analytisch te beschrijven. Een simulatie is de techniek bij uitstek om tot realistische resultaten te komen. Platooning wordt hier dan veroorzaakt door een stroomopwaarst gelegen signaal. 27
28 2.2 Eigenschappen van voertuigen in de verkeersstromen Toevoer en afvoer van wagens De aanvoer van wagens aan een kruispunt wordt meestal bepaald door stroomopwaarts gelegen verkeerssituaties. Zoals eerder reeds vermeld, oefent een kruispunt een specifieke invloed uit op het distributiepatroon waarmee wagens aangeleverd worden aan een volgend kruispunt. In de verkeerstheorie worden er vaak exponentiële distributies aangenomen. Indien er wagens aangevoerd worden van buiten het bestudeerde netwerk, wordt daarom vaak voor een exponentiële distributie gekozen. Exponentiële distributies hebben als belangrijke eigenschap dat de verschillende opeenvolgende evenementen onafhankelijk van elkaar zijn. Bij de afvoer wordt er, indien wagens zonder belemmering de wachtrij kunnen uitrijden, ook vaak geopteerd voor een exponentiële verdeling, al is het soms gewenst een constant uitrijdebiet aan te nemen. In het model kan er expliciet gekozen worden voor exponentiële of constante uitrijprocessen. Wanneer er echter verkeerslichten staan op het kruispunt is er sprake zijn van dichotome distributies. Er wordt dan tijdens de roodtijd een uitrijcapaciteit 0 gehanteerd. Tijdens de groentijd wordt er voornamelijk met constante of exponentiele uitrijdistributies gewerkt. Op een bepaald moment moet een keuze gemaakt worden voor de graad van detaillering. Indien dit meer aangewezen is kunnen andere verdelingen zoals een verschoven exponentiele verdeling of Hyper-Erlang verdeling gebruikt worden. Vaak zijn deze verdelingen ook maar benaderingen en is het meer opportuun om simpelweg de simulatie te laten lopen, waardoor er vaak veel realistischere en analytisch veel moeilijker definieerbare verkeerspatronen te voorschijn komen. Indien men beschikt over praktijkgegevens kunnen die ook gebruikt worden. 28
29 2.2.2 Gap-acceptatie en follow-up time Belangrijke parameters voor het berekenen van capaciteiten en vertragingen zijn de zogenaamde kritische gap en de follow-up tijd. De kritische gap is de minimale afstand (meestal uitgedrukt in seconden) die elke bestuurder minstens wil hebben tussen twee wagens in de stroom die hij wil kruisen vooraleer hij zal vertrekken. De follow-up tijd is de tijd waarop de volgende bestuurder de voorgaande volgt. In de modellering kunnen deze twee parameters onafhankelijk van elkaar gekozen worden. Grossman(1988) toonde aan dat, wanneer er realistischere distributies worden gekozen, dat dan de capaciteit van het kruispunt daalt. Er wordt echter vaak van een exponentiële verdeling van de gaps tussen de wagens uitgegaan. Grossman (1991)en Troutbeck (1986) toonden aan dat indien hier met meer realistische distributies zou gewerkt worden een toename van de capaciteit zou gevonden worden die van de zelfde grootorde is als deze daling. De invloed van het constant veronderstellen van deze waarden is dus verwaarloosbaar. Daarom worden de kritische gap en de follow-up tijd verondersteld een constante distributie te hebben. Dit wil zeggen dat ze, nadat ze eenmaal vrij gekozen zijn, constant blijven tijdens de simulatie. Om het aantal voertuigen te schatten dat bij een bepaalde gaplengte door deze gap zal passeren, baseer ik me op aannames gemaakt door bvb. Harders (1976) en Troutbeck (1986). Het aantal voertuigen n dat een gap zal passeren wordt gegeven door volgende kansfunctie 13 : 13 Bij het opstellen van deze kansen gaat men er vanuit dat er zich een onbeperkt aantal wagens in de wachtrij bevinden. Indien het aantal wagens in de wachtrij beperkt is, dan zal maximum deze hoeveel wagens de wachtrij kunnen verlaten. Indien het aantal auto s dat kan oversteken groter is als het aantal wachtende wagens, dan veronderstelt men dat alle wagens de wachtrij verlaten. 29
30 2.3 Aspecten met kleinere prioriteit In dit deeltje worden kort enkele aspecten besproken die, hoewel ze zeer interessant zijn, niet worden meegenomen in de modellering. Enerzijds omdat ze niet in de lijn van de thesis liggen of anderzijds omdat bepaalde fenomenen zich maar in zeer specifieke gevallen voordoen of omdat hun invloed te beperkt is Voetgangers De invloed van voetgangers op de verkeersafwikkeling op kruispunten is vaak niet gering. Zeker op kleinere kruispunten waar veel voetgangers passeren spelen ze een belangrijke rol. Het gedrag van voetgangers is echter veel moeilijker te modelleren als dat van auto s. Voetgangers moeten veel minder als wagens een vaste baan volgen. Ook zijn ze minder geneigd zich te houden aan verkeersregels. Omdat ze bovendien weinig invloed uitoefenen op de interacties tussen verkeersstromen op kruispuntvlakken zelf, houdt de simulatie er geen rekening mee Vertraging door het wisselen van rijstrook Wanneer auto s van rijstrook wisselen, kunnen de betrokken verkeersstromen hierdoor een vertraging ondervinden. Dit effect wordt in deze thesis niet bestudeerd Knipperlichten Het verspringen van een gewoon verkeerslicht naar een knipperlicht kan een zeer grote invloed hebben op de verkeersafwikkeling. Dit gebeurt echter maar zelden, en maar op een beperkt aantal kruispunten. Het fenomeen is te detaillistisch om het mee te nemen in de modellering. 30
31 2.3.4 Headway compressie Wanneer meerdere wagens achter elkaar vanuit stilstand een rijstrook afrijden zullen hun respectievelijke follow-up tijden afnemen tot een bepaalde minimale waarde. Lin & Thomas (2005).Het probleem is vaak dat er geen praktijkwaarden gekend zijn, waardoor een betere fit met betrekking tot de realiteit niet altijd gegarandeerd is Dynamische verkeerslichtenregeling Een dynamische verkeerslichtenregeling varieert de groen- en roodtijden met het aantal auto s in de wachtrijen en/of met de afstand tussen verschillende wagens in de verschillende stromen. In de thesis wordt verondersteld dat de verkeerslichten statisch werken, nl. dat de groen en rood tijden al op voorhand gekend zijn. Indien de modellering verder uitgebouwd wordt hoeft het niet zo moeilijk te zijn om een dynamische verkeerslichtenregeling te implementeren. 31
32 3 Conceptuele uitwerking van het model In het vorige hoofdstuk werden verschillende aspecten van de verkeersafwikkeling op kruispunten besproken. In dit hoofdstuk wordt uiteengezet hoe te werk is gegaan bij het opstellen van een model dat al deze verkeersaspecten op een realistische manier kan simuleren. Hierbij worden zowel de concepten die aan de basis van het model liggen als meer praktische aspecten besproken. De bedoeling is om de lezer een algemeen inzicht te verschaffen in de werking van de simulatie, zonder al te diep in te gaan op al de finesses van het programma. In Bijlage A: Werking van de simulatie wordt er dieper ingegaan op de structuur en de werking van het programma en haar verschillende functies. In het volgende hoofdstuk zullen de resultaten uit de simulatie gestaafd worden door na te gaan hoe goed de resultaten uit de simulatie de theorie en haar analytische en deterministische formules benaderen. 3.1 Het Black Box Concept Omdat met hetzelfde simulatieprogramma kruispunten met zeer verschillende typologieën moeten geanalyseerd kunnen wordt in de opbouw van een kruispunt dat men wil gaan simuleren steeds vertrokken van zeer algemene bouwstenen die later verfijnd kunnen worden volgens de specifieke eigenschappen van het kruispunt. Deze bouwstenen, de black boxes, hebben een aantal eigenschappen die door de gebruiker van het simulatieprogramma moeten worden ingevuld. Nadat deze eigenschappen toegekend zijn aan de black boxes kunnen ze op zulke wijze met elkaar gelinkt worden dat ze een goede voorstelling van een kruispunt of van een verkeerssituatie vormen. Een kruispunt kan worden opgedeeld in verschillende fysische oppervlaktes waar voor alle wagens die zich op deze oppervlakte bevinden, dezelfde externe condities gelden. In grote lijnen kan gesteld worden dat deze fysische entiteiten overeenstemmen met verschillende (wacht)rijen 14 of verkeersstromen die men aan en op het kruispunt kan onderscheiden. 14 In de tekst worden de benamingen black box, wachtrij en rij gebruikt. Ze doelen in de context van deze thesis allen op hetzelfde, nl. op de basisbouwstenen waaruit het kruispunt in de simulatie wordt opgebouwd. Black box refereert naar de wijze waarop deze bouwstenen worden behandeld in de simulatie, terwijl wachtrij eerder naar de onderliggende wachtrijtheorie refereert. De benaming rij stamt uit de fysische rijen die zich op het kruispunt vormen. Wanneer dus over een wachtrij wordt gesproken wil dit dus niet zeggen dat de wagens die zich in dit fysische kruispuntdeel bevinden ook effectief zullen moeten wachten (cfr. black box 3 in figuur 1) 32
33 In het simulatiemodel worden deze delen vertegenwoordigd door verschillende black boxes, die allen gekenmerkt worden door een nummer. Figuur 1: Voorstelling van black boxes In figuur 1 is de T-kruising opgedeeld in 3 delen. Deze delen stemmen overeen met 3 fysische delen van het kruispunt die verschillende randvoorwaarden hebben. De wagens die deel 1 en deel 2 uitrijden komen allemaal in deel 3 terecht. De auto s uit deel 1 worden hierbij niet belemmerd, terwijl de auto s uit deel tweevoorrang zullen moeten geven aan de wagens uit rij 1. De auto s komen van buiten het beschouwde gebied het gebied binnen via rijen 1 en 2. Ze doen dit volgens bepaalde statistische verdelingen. Via rij 3 rijden de wagens het beschouwde gebied weer buiten. De benaming black box stamt uit het idee dat perfect geweten is welke auto s een deel binnenrijden, en hoe ze er weer uitrijden. Ze doen dit volgens het first-in-first-out-principe (FIFO). Binnen de black box kan er niets aan de volgorde van deze wagens veranderd worden. Indien men het gevoel heeft dat er binnenin de black box toch enige aanpassingen moeten gebeuren, wil dit zeggen dat deze box te groot gekozen is, en dat hij opgesplitst moet worden in een aantal andere, kleinere boxen. Hier wordt later nog op teruggekomen. 33
34 3.2 Eigenschappen van de verschillende black boxes Het algemene karakter van de black boxes Initieel zijn de verschillende black boxes of wachtrijen gebaseerd op Markov-rijen. Een wachtrij in de simulatie functioneert analoog als een Markov geboorte- sterfteproces. Er worden namelijk wagens toegeleverd (geboorte) en er vertrekken wagens (sterfte). De populatie, het aantal wagens dat zich in de wachtrij bevindt, neemt hierdoor met 1 toe of neemt hierdoor met 1 af. Een belangrijke eigenschap van Markov-rijen is dat de volgende toestanden waarin deze rijen zich zullen bevinden enkel afhangen van de huidige toestand, en niet van de vorige toestanden. Een Markov-proces heeft dus geen geheugen. Voor elke box moet eerst en vooral een distributie voor aankomst en vertrekprocessen gekozen worden. In de simulatie heeft men de keuze tussen een constante of een exponentiële distributie, beide gekenmerkt door hun gemiddelde waarde. Indien dit wenselijk is kunnen er ook andere distributies gekozen worden. Zeker indien men over metingen beschikt is dit zeer zinvol. De karakteriserende gemiddelde waarde wordt voor de aankomstprocessen de aankomstintensiteit of arrivalrate (wagens/sec) en voor de vertrekprocessen de bedieningsintensiteit of servicerate (wagens/sec) genoemd. Het omgekeerde van deze intensiteiten kent men als respectievelijk de interarrival time en de interdeparture time. Door het kiezen van een distributie voor de aankomsten en vertrekken, wordt een eerste onderscheid gemaakt tussen de verschillende rijen. 34
35 3.2.2 Het specifieke karakter van black boxes Verkeerslichten Nadat een keuze is gemaakt voor een distributie, worden de wachtrijen verder geïndividualiseerd door aan te geven of op het einde van de rij al dan niet een verkeerslicht staat. Indien dit het geval is, moeten ook de groen- en roodtijden bepaald worden. Indien het licht op rood staat valt de bedieningsintensiteit logischerwijze terug tot 0. In de simulatie kunnen de verkeerslichten van de verschillende wachtrijen op elkaar worden afgestemd. Hiertoe moet worden aangegeven hoeveel tijdseenheden na de start van de simulatie de wachtrij voor het eerst rood licht zal krijgen. Dit noemen we de offset. Figuur 2: Voorstelling van offset en cycluslengtes In figuur 2 is ook duidelijk te zien dat men door een juiste keuze van de cycluslengtes en offsets ook rekening kan houden met een klein interval waarin beide stromen rood licht hebben (all red interval). 35
36 Capaciteit Een andere belangrijke eigenschap van de black boxes is dat ze een gelimiteerde inhoud kunnen hebben. Wanneer deze maximale capaciteit bereikt is zullen er geen andere voertuigen meer bij passen totdat er door een vertrek uit de wachtrij weer plaats gecreëerd is. Indien men dit wil kan de capaciteit ook ongelimiteerd verondersteld worden. In figuur 3 worden de verschillende eigenschappen van black box schematisch weergegeven. Figuur 3: Karakteristieke eigenschappen van de black box 36
37 3.3 Interacties tussen de verschillende wachtrijen Naast het ingeven van de karakteristieke eigenschappen van de verschillende rijen, moet er ook worden aangegeven welke de onderlinge relaties tussen deze verschillende rijen zijn Toelevering In plaats van dat de wagens een rij binnenrijden volgens een vooraf bepaalde aankomstendistributie kan er ook geopteerd worden om een rij, met haar uitrijdende auto s, de leverancier te laten zijn voor een andere rij. Deze tweede rij krijgt haar populatie dan toegeleverd via andere rijen. Omdat het in de simulatie mogelijk gemaakt is om verschillende rijen toe te laten leveren aan eenzelfde rij, zullen veel ingewikkeldere, analytisch moeilijk te beschrijven aanleveringsdistributies kunnen gesimuleerd worden. Hierdoor stijgt het realiteitsniveau van de simulatie sterk. Uiteindelijk is het de bedoeling om de grote meerderheid van de rijen toegeleverd te laten worden. Enkel de rijen waarlangs de voertuigen het beschouwde systeem binnenrijden zullen nog aangeleverd worden volgens vooraf expliciet bepaalde distributies op-1-toelevering De black boxes kunnen andere wachtrijen op verschillende manieren aanleveren. De makkelijkste wijze is om te stellen dat alle wagens die een bepaalde rij uitrijden, allen aan een zelfde andere rij worden toegeleverd. Het is dan makkelijk om de verschillende vertragingen van de verschillende voertuigen te berekenen omdat men precies weet welk traject elke wagen afgelegd heeft. We noemen dit de 1-op-1-toelevering. Deze wordt schematisch voorgesteld in figuur 4. Figuur 4: Schematische voorstelling traject bij 1-op-1-toelevering 37
38 Wanneer men meerdere verschillende typologieën voor eenzelfde kruispunt wil vergelijken kan men de simulatie een aantal keer laten lopen voor deze verschillende indelingen. Elke simulatie is echter anders. Om tot exact vergelijkbare resultaten te komen is er een tool ingebouwd die een wagen die uit een wachtrij uitrijdt toelevert aan meerdere andere rijen tegelijk. Er wordt dan gesproken over een 1-op-1-toelevering aan verschillende rijen (cfr. figuur 5). Deze andere rijen kunnen dan inputs zijn voor verschillende deelsystemen, bvb. de verschillende typologieën die men wil vergelijken. Hierdoor wordt veel sneller duidelijk welke indeling het meest aan de noden voldoet. Het systeem is weergegeven in onderstaande figuur. Bovendien zal dit ook een noodzakelijke tool blijken om gap-acceptatie op een realistische wijze te modelleren. Dit wordt verder in de tekst uiteengezet. Figuur 5: 1-op-1-toelevering aan verschillende rijen 38
39 op-m-toelevering Vaak rijden auto s die in 1 wachtrij staan nadien verschillende richtingen uit. Denk hierbij bvb. aan gedeelde opstelstroken. Daarom is het in de simulatie voorzien dat wachtrijen kunnen toeleveren aan verschillende wachtrijen. In de simulatie zijn er twee criteria volgens dewelke dit kan gebeuren voorzien: toelevering aan de leegste rij of toelevering aan verschillende rijen met een bepaalde kans. Bij de toelevering aan de leegste rij worden de uitrijdende auto s geleverd aan de rij waarin de minste wachtenden staan. Zo zijn aan verkeerslichten alle rijen meestal ongeveer even lang. Wanneer men een idee heeft over het percentage automobilisten dat rechtdoor rijdt, links- of rechtsaf slaat, dan kan volgens deze percentages de beweging van de wagen geloot worden. In figuur 6 is een voorbeeld van een 1-op-m-toelevering getekend. Figuur 6: Procentuele 1-op-m-toelevering 39
40 Wanneer de maximale capaciteit van één van de toegeleverde rijen bereikt is, kunnen er aan deze rij natuurlijk geen wagens meer worden toegeleverd. Het aantal verschillende rijen waaraan zo kan worden toegeleverd is in principe onbeperkt. Er zijn vele verkeerssituaties waarvoor het gebruik van deze wijze van toeleveren noodzakelijk is om tot een realistische simulatie te komen. De capaciteiten van verschillende verkeersstromen over het kruispunt bij een 1-op-m-toelevering worden even makkelijk berekend als bij een 1-op-1-toelevering. Het is echter veel moeilijker om de gemiddelde vertragingen voor de verschillende wagens te berekenen. Men kan immers niet meer op voorhand het traject van de verschillende wagens voorspellen, wat het programmeren van functies om deze vertragingen te berekenen veel moeilijker maakt. In figuur 7 een vereenvoudigde voorstelling gemaakt van een situatie waarin het traject dat de verschillende wagens volgen niet meer op voorhand vastligt. Wachtrij 3 stelt hier dan bvb. een sluipweg die gebruikt wordt wanneer er zich te veel wagens in rij 2 bevinden. Daarom is er een labelsysteem uitgewerkt dat continu het verloop van het traject van de verschillende auto s bijhoudt, samen met hun reistijd. Dit labelsysteem wordt gedetailleerder besproken in bijlage A. Figuur 7: Voorbeeld van situatie waar traject niet meer op voorhand vastligt 40
41 3.3.2 Hinder en vermindering Wanneer bepaalde rijen te lang worden kunnen ze andere rijen hinderen. Zo worden wagens verhinderd hun wachtrij uit te rijden wanneer er geen plaats meer is op de opstelstrook waar ze heen willen. Wanneer men aangeeft dat een rij een andere rij hindert, dan moet ook steeds de populatiegrootte vanaf dewelke deze hinder optreedt worden aangegeven. Wanneer de hinderende rij dit aantal auto s heeft bereikt, dan valt de bedieningsintensiteit van de gehinderde rij naar 0. Er kunnen dan geen wagens de rij meer uitrijden. Onder vermindering wordt verstaan dat de bedieningsintensiteit van een rij afneemt vanaf wanneer de minderende rij een bepaalde lengte heeft. De intensiteit daalt dan wel, maar wordt zeker niet nul. Van zodra de lengte van de hinderende of verminderende rij weer kleiner wordt, zodat haar hinder weer verdwijnt, krijgt de gehinderde rij weer haar oude vertrekintensiteit. Afhankelijk van het proces dat men wenst te modelleren zal voor 1 van deze twee of een combinatie van deze twee tools (hinder of vermindering) moeten worden gekozen. Zo zal er het best voor een complete hindering gekozen worden wanneer de opstelcapaciteit van een rij beperkt is. De uitrij-intensiteit van andere rijen die aan deze rij leveren valt terug tot nul wanneer haar maximale capaciteit bereikt is. In andere gevallen wordt het uitrijden van bepaalde rijen bemoeilijkt doordat een andere rij een zekere capaciteit bereikt heeft. Toch zullen er nog steeds wagens kunnen vertrekken, zij het aan een verlaagde intensiteit. Deze twee gevallen worden weergegeven in figuur 8. Figuur 8: Voorstelling reële hinder en vermindering 41
42 3.3.3 Voorrang en gap-acceptatie Om een voorrangssituatie te modelleren is een goed inzicht vereist in de werking van het black box systeem. In dit deel wordt uiteengezet hoe men in de simulatie zulk een voorrangssituatie modelleert. Er wordt hiertoe een speciaal soort wachtrij geïntroduceerd; De gap-acceptatie rij. Deze rij heeft geen fysische betekenis, maar wordt enkel gebruikt om de kritische gap en de follow-up tijd te kunnen modelleren. In figuur 9 wordt schematisch aangegeven hoe een reële voorrangssituatie vertaald wordt naar de simulatie Figuur 9: Omzetting voorrangssituatie naar model Er wordt een kruising van twee stromen beschouwd. De ene stroom (hoofdstroom) heeft voorrang op de andere (zijstroom). Wanneer er zich een wagen uit de hoofdstroom op het kruispuntvlak bevindt, wordt het uitrijden van de wagens uit de zijstroom verhinderd. Ze geven voorrang. De afstand tussen twee wagens uit de hoofdstroom moet zelfs groter zijn dan de kritische gap vooraleer er een wagen vertrekt. Om dit te kunnen modelleren is er een gapacceptatie wachtrij gecreëerd. Deze wachtrij wordt toegeleverd door de hoofdstroom en heeft een capaciteit 1. Wanneer er zich een nieuwe toelevering van een nieuwe wagen voordoet terwijl er zich al een auto in deze rij bevindt, dan wordt de auto die zich reeds in de wachtrij bevond uit de rij gestoten door de nieuwe wagen. 42
43 De bedieningstijd van de gap-acceptatie rij is constant. Een wagen die de rij binnenkomt zal x aantal seconden later bediend worden. De bedieningstijd moet gelijk genomen worden aan de kritische gap tijd. Wanneer een wagen bediend werd vooraleer hij uit de gap-acceptatie rij geduwd is 15, wil dit zeggen dat de tussentijd tussen twee wagens in de hoofdstroom groter is dan de kritische gap tijd. Door nu nog aan te geven dat de gap-acceptatie rij de zijstroom hindert wanneer er zich een voertuig in bevindt, zal op deze wijze het systeem van gap acceptatie gemodelleerd kunnen worden. De bedieningsintensiteit van de wachtrij voor de voertuigen uit de zijstroom is het 0,5/ Tfollow-up 16 voor het eerst vertrekkende voertuig, en 1/Tfollow-up voor de daarop volgende voertuigen. Zo wordt ook de follow-up tijd gemodelleerd zoals in vorig hoofdstuk aangegeven. Een bedieningstijd betekent tevens ook een vertragingstijd. Indien een wagen immers een rij met een constante bedieningstijd van 5 seconden binnenrijdt, dan komt hij deze rij ten vroegste 5 seconden later weer buiten. Het voertuig wordt vertraagd door deze rij. Wanneer een wagen een kruispuntvlak kruist wanneer hij voorrang heeft doet hij doet hij dit echter vaak in een zeer beperkte tijdsspanne. De wagens uit de hoofdstroom zouden in de gapacceptatie rij te zeer vertraagd om nog in overeenstemming te zijn met de werkelijkheid. Daarom worden de aanrijdende auto s zowel aan de gap-acceptance als een aan andere rij toegeleverd. Dit is te zien op figuur 9. Het is hier dat de eerder besproken 1-op-1-toelevering aan verschillende rijen noodzakelijk is. Er ontstaan als het ware voertuigen. De wagens die de gap-acceptatie rij uitrijden worden daarom nergens toegeleverd, en verloren verondersteld om een onterechte toename van wagens in het systeem te vermijden. De gap-acceptatie rij wordt hierdoor een instrument om een proces te modelleren, eerder dan dat ze een fysische betekenis heeft. 15 Op dit moment is de gap-acceptatie rij dus leeg aangezien de maximale capaciteit beperkt is tot Dat de eerste wagen die de rij uitrijdt bedient wordt met uitrij-intensiteit 0,5/Tfollow-up is speciaal zo geprogrammeerd om de simulatie in overeenstemming te brengen met de veronderstellingen van Harders (1976) en Troutbeck (1986) die eerder al werden aangehaald. 43
44 In dit deel werd uiteengezet hoe een voorrangssituatie gemodelleerd wordt. Uit dit voorbeeld komt duidelijk naar voor dat niet alle rijen een fysische tegenpool moeten hebben. De wachtrijen kunnen geïnstrumentaliseerd worden. Een goed inzicht in de werking van de black boxes en in de vertaling van de fysische werkelijkheid naar een model maakt het mogelijk complexere situaties te modelleren. 3.4 Omzetten van werkelijkheid naar model De vertaling van de werkelijkheid naar het model is niet altijd even eenvoudig. In dit deel wordt een algemene werkwijze besproken die een goede omzetting van de realiteit garandeert. Het is echter niet altijd de meest gedetailleerde vertaling die het meest aangewezen is. Wanneer men het effect van een bepaald fenomeen wil onderzoeken is het zinloos om delen van het kruispuntvlak die op dit fenomeen geen invloed hebben al te gedetailleerd te modelleren. Dit zou enkel onnodige rekenkracht van de computer vergen. Daarom is er ook een systeem uitgewerkt om de graad van detaillering van de modellering te bepalen Definiëren van de wachtrijen De verschillende wachtrijen worden uiteindelijk op zulke wijze gecombineerd dat ze een aaneengesloten netwerk van schakels vormen. Elke schakel stelt dan een deeltje van het kruispunt voor. Deze kunnen geklasseerd worden volgens hun graad van detaillering. We kunnen spreken over level-1, -2- of 3-rijen. De grofste graad van detaillering zijn de level-1- rijen. Wanneer men meer en meer inzoomt op de verschillende processen worden er rijen van level 2 of level 3 teruggevonden. 44
45 Level-1-rijen De eerste stap in de omzetting van realiteit naar model is het bepalen van alle mogelijke banen die op het kruispuntvlak kunnen beschreven worden. Wanneer over eenzelfde stuk weg in twee verschillende richtingen kan gereden worden, dan worden er ook twee banen getekend. Verschillende rijstroken worden ook best als verschillende wachtrijen gemodelleerd. Deze banen kunnen splitsen in nieuwe banen, of kunnen samenkomen om een gemeenschappelijke baan te vormen. In de punten waar dit gebeurt plaatsen we knopen. Ook ter hoogte van alle verkeerslichten worden knopen geplaatst. Al deze knopen noemen we level-1-knopen. In figuur 10 zijn deze level-1-knopen aangegeven door zwarte stippen. De schakels tussen deze knopen zijn de level-1-rijen. Het netwerk dat zo ontstaat, kan vergeleken worden met bvb. een hydraulisch netwerk waarin ook stromen samenkomen en weer splitsen. Het grote verschil met zo een hydraulisch netwerk is dat bepaalde stromen elkaar kunnen kruisen zonder dat er enige vorm van menging is tussen de verschillende stromen. De knopen waar stromen kruisen zonder te mengen of te splitsen worden level-2 of 3-knopen genoemd Level-2-rijen Level-2-knopen ontstaan waar level-1-rijen die gelijktijdig groen licht kunnen hebben, kruisen zonder te mengen. Op een kruispunt zonder verkeerslichten worden alle stromen verondersteld steeds groen licht te hebben. Door het plaatsen van level-2-knopen worden verscheidene level-1-rijen in stukken gesplitst. Bij elke kruising van twee level-1-rijen kunnen er 4 level-2-rijen ontstaan. Volgens het verkeersregelement is er echter altijd 1 van de twee stromen die voorrang moet geven aan de andere. Wanneer verondersteld wordt dat de stroom die voorrang krijgt nooit gehinderd zal worden, dan blijft de rij die voorrang heeft een level-1- rij. Indien men toch een kans op hinder vermoedt dan wordt deze rij toch ook een level-2-rij. De wachtrij die voorrang moet geven wordt sowieso opgesplitst in 2 nieuwe wachtrijen. In figuur 10 zijn de level-2-knopen aangegeven met rode stippen. 45
46 Figuur 10: Schematische voorstelling van interacties op een kruispunt Level-3-rijen De knopen die nu nog overblijven zijn de knopen waar normaal gesproken geen interacties tussen stromen plaatsvinden. De wagens die de banen volgen die elkaar in deze knopen kruisen hebben immers nooit op hetzelfde tijdstip groen licht. Toch zijn er ook hier nog knopen te onderscheiden waar de waarschijnlijkheid op interacties groter is als in andere level-3-knopen. Het verschilt echter van situatie tot situatie in welke knopen deze interacties zich zullen voordoen, en het is moeilijk om hier nog algemene regels op te plakken. Algemeen gesproken doet men er best aan ook al deze mogelijke interacties mee te nemen in de modellering. Enkel indien men delen van het kruispunt niet wenst te beschouwen of vereenvoudigd voorstelt kan men deze knopen verwaarlozen. In de figuur zijn deze knopen weergegeven met blauwe stippen. 46
47 Nummering Nadat het kruispunt in de verschillende delen is opgesplitst, moet aan de verschillende rijen nog een rijnummer worden toegewezen. De nummering start bij 1 en loopt tot het aantal rijen waarin het systeem is opgesplitst. Deze nummering is in principe willekeurig, al zal het voor de gebruiker van de simulatie handig zijn om een voor zichzelf een logische nummering te maken. Daarna moet nagegaan worden of er nog extra rijen toegevoegd moeten worden om voorrangssituaties te kunnen modelleren. In dit deel werd een methode aangegeven om tot een goede opsplitsing van het kruispunt te komen. Zoals eerder gesteld is het zaak om een juiste balans te vinden in de graad van detailleren. Niet alleen een goede opsplitsing zal leiden tot een realistisch resultaat. Ook het juiste aangeven van de interacties tussen de verschillende rijen heeft een grote invloed op het resultaat. Hoe men hierbij te werk gaat wordt in de volgende paragraaf aangegeven Aangeven van interacties Nadat het kruispuntvlak in verschillende delen opgesplitst is moeten vooreerst de black box eigenschappen van de rijen worden ingekleurd. Hierbij zullen vele eigenschappen niet willekeurig te kiezen zijn. De capaciteiten van de verschillende rijen hangen af van de opstelruimte die men op het kruispunt heeft, en de cyclustijden van de verkeerslichten zijn vaak ook reeds gekend 17. Enkel voor de rijen die van buiten het beschouwde systeem toegeleverd worden, moet een aankomstendistributie gekozen worden. Voor de andere rijen moet worden aangegeven door welke rij ze worden aangeleverd. De vertrekken worden meestal exponentieel verdeeld verondersteld. Door het uitvoeren van de simulatie verandert deze distributie reeds snel in andere, meer reële distributies door de invloed van verkeerslichten of andere wachtrijen. De percentages voertuigen die elk een andere richting opgaan bij het splitsen van een stroom moeten ook geschat en aangegeven worden. 17 Door de verkeerslichtenregeling aan te passen kan men de invloed ervan op de verkeersafwikkeling bestuderen. 47
48 Een andere moeilijkheid stelt zich bij het schatten van de vermindering van vertrekintensiteit wanneer een rij gehinderd wordt door een andere. Deze intensiteitsdaling is namelijk sterk afhankelijk van kruispunt tot kruispunt, en van bestuurder tot bestuurder. Indien men een bestaand kruispunt simuleert, kan men best enkele metingen uitvoeren, of zich baseren op bestaande metingen van bij gelijkaardige kruispunten. Indien men niet over deze gegevens kan beschikken maakt men een realistische schatting. 3.5 Tel- en tijdmatrices Om na de simulatie de vertragingen, de capaciteiten en de wachtrijlengtes te kunnen berekenen worden alle bewegingen naar of vanuit de black boxes opgeslagen. Hiervoor staan de telmatrix en de tijdmatrix ter beschikking. In tabel 1 is een deel van de tijdmatrix en de telmatrix voor een toelevering van rij 1 naar rij 2 weergegeven. In rij 1 komen auto s toe volgens een exponentiele verdeling, en uit rij twee vertrekken ze ook volgens een exponentiele verdeling. De tabel moet op volgende wijze gelezen worden; Men kijkt in de telmatrix of er een verandering geweest is van het aantal wagens in de wachtrij. In de tijdmatrices worden zowel de tijdstippen van populatietoename als afname bijgehouden. Van de eerste naar de tweede rij in de matrix is er een afname van de teller van de eerste wachtrij van 3 naar 2. In de tijdmatrix vindt men in de overeenkomstige kolom en rij, het tijdstip terug waarop deze overgang naar een nieuwe populatiegrootte plaatsvond. De overgang 3 naar 2 wagens voor wachtrij 1 voltrok zich dus op tijdstip 80,3566. Omdat rij 1 toelevert aan rij 2 impliceert een vertrek uit rij 1 een aankomst in rij 2. Er kan dan ook afgelezen worden dat de populatie van rij 2 gegroeid is van 4 naar 5, en dit op tijdstip 80, ,001 tijdseenheden nadat de wagen rij 1 verliet komt hij aan in rij 2. Dit overgangsverlies kan zelf gekozen worden. Uit de telmatrix kan afgelezen worden dat van tijdstip 76,9635 tot tijdstip 80,3566 de populatie van wachtrij 1, 3 was. Van 80,3566 tot 81,5149 was deze populatie 2 Zo kunnen uit de tijd- en telmatrices de gemiddelde wachtrijlengtes berekend worden. In de bijhorende figuur 11 is de populatie van beide rijen gedurende het tijdsinterval 0 tot 100 weergegeven in functie van de tijd. Er is duidelijk op te zien dat wanneer er een afname is van de populatie van wachtrij 1 (blauw), er zich tegelijkertijd een toename van de populatie van wachtrij 2 (rood) voordoet. 48
49 tijd rij 1 tijd rij 2 tel rij 1 tel rij Tabel 1: Deel van een tijd- en telmatrix 7 populatiegrootte in functie van de tijd; blauw : rij 1, rood : rij populatiegrootte bedienings- en aankomstintensiteiten; (1auto/6sec) X-as:tijd Figuur 11: Populatiegrootte in functie van de tijd 49
50 3.6 Labelsysteem Wanneer het individuele traject dat elke wagen aflegt op voorhand niet exact kan worden bepaald, dan kan men niet zonder meer de verschillende vertragingen die de voertuigen hebben opgelopen uit de tel- en tijdmatrices aflezen. Het blijft nog wel mogelijk om de capaciteit van het kruispunt te berekenen, en om daaruit de gemiddelde vertragingen te berekenen. Meestal volstaan deze gegevens, al zou men ook geïnteresseerd kunnen zijn in de vertraging die elk individueel voertuig heeft opgelopen. Om deze berekeningen in verband met de vertragingen ook in deze gevallen mogelijk te maken is er een labelsysteem ontwikkeld. In dit labelsysteem wordt het traject dat elke wagen heeft afgelegd, samen met de tijden die de verschillende voertuigen op de verschillende kruispuntsecties hebben doorgebracht, bijgehouden in 2 matrices, de aankomst en vertrek labelmatrix. De labels zijn kommagetallen. Een label geeft aan welk traject een wagen reeds doorlopen heeft. De getallen voor de komma stellen eenheden voor, terwijl de getallen na de komma duiden op tientallen. De getallen op de eerste plaats voor en na de komma vormen een koppel. De getallen op de tweede, derde, plaats voor en na de komma vormen zo ook allen een koppel. Het eerste getal voor de komma vormt samen met het eerste getal na de komma het rijnummer van de laatste rij waarin de wagen zich bevond. Het tweede getal voor de komma vormt, samen met zijn pendant achter de komma, het rijnummer van de voorlaatste rij, enz. Hierbij geeft het getal na de komma steeds het tiental aan, terwijl het getal voor de komma op het aantal eenheden wijst. Ter verduidelijking wordt er een klein voorbeeldje gegeven. Voorbeeld: Label 321,110 duidt op een traject van rij (0x10+3) naar (1*10+2) naar (1*10+1). Of dus het traject Label 47124,30275 duidt zo op traject Voor een gedetailleerdere uitleg over de precieze werking wordt verwezen naar bijlage A: werking van de simulatie. 50
51 3.7 Beperkingen in modellering Eigenlijk kent de modellering zeer weinig beperkingen. Door een goede combinatie van verschillende wachtrijen kunnen met het programma zowat alle verkeerssituaties gemodelleerd worden. Bovendien is het model zo opgesteld dat er makkelijk extra toepassingen kunnen worden ingebracht. In het model wordt er momenteel echter geen rekening gehouden met wagens met een personenauto equivalent (pae) verschillend van 1, zoals bvb. vrachtwagens. Ook een wachtrijtype waarin elke wagen een zelfde constante verblijftijd heeft, is nog niet gemodelleerd. In dit hoofdstuk werd beschreven hoe er bij het opstellen van het programma te werk werd gegaan om tot een goed model van de werkelijkheid te komen. Eerst werd het principe van de black box uiteengezet, waarna er aangetoond werd hoe men tot een goede vertaling van de werkelijkheid naar een netwerk van wachtrijen komt. In het volgende hoofdstuk zullen de resultaten die bekomen worden met de simulatie getoetst worden aan de resultaten die men zou verwachten op basis van analytische en deterministische formules die voor handen zijn in de literatuur. 51
52 4 Verificatie In het programma worden verkeersprocessen gesimuleerd door een het combineren van een aantal wachtrijen die initieel gebaseerd zijn op Markov geboorte- sterfteprocessen. Om het model theoretisch te onderbouwen worden in dit deel de resultaten uit de simulaties geëvalueerd door een grondige vergelijking met de analytische formules te maken. Om tot een goede vergelijking te komen wordt de kans om een bepaald aantal gebruikers aan te treffen in de wachtrij en de gemiddelde vertraging berekend. Ook het gemiddelde aantal wachtenden in een wachtrij wordt geverifieerd. Deze waardes leggen de basis voor goede benaderingen van gemiddelde wachtrijlengtes, capaciteiten en vertragingen in uitgebreidere systemen. In de bijlage werking van de simulatie is aangegeven hoe deze capaciteiten en vertragingen berekend worden. Vooreerst worden individuele wachtrijen bestudeerd. Aangezien de wachtrijen gebaseerd zijn op Markov-rijen, worden de resultaten die bekomen worden met de simulatie getoetst aan de resultaten die de analytische formuleringen van dit soort rijen geven. Verder worden ook interacties tussen verschillende rijen bestudeerd. Het is de bedoeling om na te gaan hoe realistisch de resultaten uit de simulatie zijn. De resultaten die hier verkregen worden zullen vergeleken worden met analytische oplossingen uit de wachtrijtheorie. De verificatie van het model is niet alleen het verifiëren van de gesimuleerde verkeersafwikkeling, maar tevens van de geprogrammeerde analysemethodes. Er worden namelijk nooit goede resultaten voor bvb. de vertraging gevonden indien de functies die deze vertraging berekenen niet juist zijn. Op zijn beurt zal een juiste methode om de vertraging te berekenen geen goede resultaten geven indien de verkeerssimulatie niet juist is. In het model zit dus een dubbele controle op fouten ingebouwd wat alleen maar meer zekerheid geeft wat de correctheid van de resultaten betreft. 52
53 4.1 Wachtrijen als Markov-rijen Eerst worden de eigenschappen van de rijen uit de simulatie vergeleken met Markov wachtrijsystemen. Deze systemen worden algemeen aangeduid met volgende notatie: X/Y/U/V, waarbij; X: Wijst op de statistische verdelingsfunctie voor het aankomstproces in de wachtrij. Y: Wijst op de statistische verdelingsfunctie voor het vertrekproces uit de wachtrij. U: Het aantal wachtrijen of servers in het systeem. V: De maximale capaciteit van een wachtrij. Als verdelingsfuncties worden in de wachtrijtheorie vaak exponentieel verdeelde functies gekozen. Deze verdeling heeft als voordeel dat de aankomsten of vertrekken onafhankelijk van elkaar verondersteld mogen worden. Een exponentieel proces wordt aangeduid met het symbool M. Er kunnen echter ook andere verdelingen gebruikt worden. Daarbij wordt dan in de eerste plaats gedacht aan constante bedieningstijden, voorgesteld door het symbool D, maar ook andere verdelingsfuncties zoals een Erlang (Er, met r de orde) verdeelde aankomstprocessen kunnen soms zeer toepasselijk zijn. Een algemeen aankomst- of vertrekproces wordt voorgesteld door een G, deze verdeling wordt gebruikt wanneer het proces niet nader gekend is. Voor het meest algemene geval kan er gedacht worden aan een dataset die als invoer voor de simulatie gebruikt wordt. Vaak wordt de maximale capaciteit van de wachtrij achterwege gelaten in de notatie. Er wordt dan impliciet verondersteld dat de rij een oneindige capaciteit heeft. Indien de populatie beperkt is, wordt er nog een vijfde symbool toegevoegd. In dit onderzoek naar verkeersafwikkeling op kruispunten wordt de populatie echter steeds oneindig groot verondersteld. 53
54 De Markov-processen die hier verondersteld worden zijn geboorte- en sterfteprocessen (birth death processes). Een gedetailleerde theoretische beschrijving van al deze processen kan teruggevonden worden in het boek Queueing systems van Kleinrock. De wachtrij bevindt zich in een bepaalde toestand k, gekenmerkt door het aantal wachtenden in de rij, de populatiegrootte. Vanuit deze toestand kan de wachtrij maar overgaan in de twee toestanden. Een overgang naar een lagere toestand k-1 door een sterfte, waardoor de populatie afneemt, of naar een hogere toestand k+1, door een geboorte, waarbij de populatie toeneemt. In figuur 12 wordt dit proces schematisch weergegeven. De populatie kan nooit kleiner worden als 0. Figuur 12: Algemene voorstelling Markov geboorte- sterfte-proces De overgangen worden gekenmerkt door λ k, de geboorte-intensiteit, en µ k, sterfte-intensiteit. Dit zijn het aantal geboortes of sterftes die verwacht worden per tijdseenheid. De kans op een geboorte of een sterfte in het tijdsinterval dt is gelijk aan respectievelijk λ k dt en µ k dt. De intensiteiten worden meestal constant gehouden voor de verschillende toestandsovergangen. Aangezien de populatie nooit kleiner kan worden als 0, is µ 0 steeds gelijk aan nul. De verhouding 1/ λ k wordt de interarrival-time genoemd. Het is het aantal tijdseenheden die verstrijken per geboorte, of dus de tijd tussen twee geboortes. 1/ µ k wordt de bedieningstijd of de servicetime genoemd. De verhouding λ/µ wordt ook aangeduid als ρ, waarbij rho de saturatiegraad is. Als een voorwaarde voor een convergeren van deze Markov-processen naar een toestand van dynamisch evenwicht geldt als voorwaarde dat deze saturatiegraad rho kleiner moet zijn als 1. 54
55 4.1.1 M/M/ De kans op populatie k De interarrivaltijden zijn hier net zoals de bedieningstijden onafhankelijk exponentieel verdeeld. Het systeem bestaat uit 1 server of wachtrij. De kansdichtheid van de exponentiële funcie is als volgt gegeven [Beirlant & Van Dyck,2001]; Hierbij is λ de gemiddelde intensiteit. 1/λ is de interarrivaltime. Soms wordt de exponentiele functie ook wel gekenmerkt met de interarrivalrate als parameter.(bvb. in Matlab). Men moet dan ook steeds even checken welke parameter gebruikt wordt om misinterpretaties en foute resultaten te vermijden. Indien de verhouding tussen de gemiddelde geboorte-intensiteit en de gemiddelde sterfteintensiteit kleiner is dan 1 zal er zich in het systeem een dynamisch evenwicht instellen. Dit dynamisch evenwicht wordt beschreven door volgende twee vergelijkingen De input waarschijnlijkheidsstroom in toestand k; I k = λ k-1 p k-1 + µ k+1 p k+1. De output waarschijnlijkheidsstroom uit toestand k; O k = (λ k + µ k) p k. Waarbij p k de kans is om in het systeem een toestand aan te treffen met een populatie k. In het dynamische evenwicht moeten deze twee stromen aan elkaar gelijk zijn.dit resulteert in volgende gelijkheid; λ k-1 p k-1 + µ k+1 p k+1= (λ k + µ k )p k. Deze gelijkheid geldt voor alle k s. λ k en µ k zullen allen dezelfde verondersteld worden. µ 0 is echter gelijk aan 0. 55
56 Uiteindelijk leidt dit tot een stelsel van vergelijkingen, waarbij µ.p 1 = λ. p 0 λ.p 0 +µ.p 2 = (λ+ µ). p 1 λ.p k-1 +µ.p k+1 = (λ+ µ). p k Dit stelsel kan herschreven worden naar een matrixvergelijking; Waaruit de oplossing kan worden gehaald in functie van p 0 ; λ p k = p 0. µ k. De som van al deze kansen sommeert tot 1 waaruit dan p 0 berekend kan worden als p 0 = 1- µ λ. rho < 1 is de voorwaarde voor convergentie naar een eindige oplossing. Indien rho > 1, dan zal de wachtrijpopulatie divergeren en worden geen bruikbare resultaten gevonden. Uiteindelijk wordt als algemene oplossing gegeven verkregen; p k = (1 ρ)ρ k met k=0,1,2, 56
57 In tabel 2 worden de resultaten uit de theorie vergeleken met deze bekomen door simulatie. populatie P k 0,4945 0,2523 0,1279 0,0688 0,0291 0,0120 0,0071 0,0034 0,0019 0,0013 0,4942 0,2429 0,1257 0,0656 0,0353 0,0177 0,0117 0,0035 0,0015 0,0013 0,5015 0,2488 0,1206 0,0629 0,0331 0,0160 0,0083 0,0056 0,0019 0,0010 0,5042 0,2509 0,1216 0,0931 0,0293 0,0157 0,0080 0,0035 0,0026 0,0011 0,5002 0,2536 0,1247 0,0569 0,0336 0,0172 0,0080 0,0032 0,0023 0,0009 gemiddelde 0,4989 0,2497 0,1241 0,0695 0,0321 0,0157 0,0086 0,0039 0,0020 0,0011 St. dev. 0,0044 0,0042 0,0030 0,0139 0,0028 0,0022 0,0018 0,0010 0,0004 0,0002 theorie 0,5000 0,2500 0,1250 0,0625 0,0313 0,0156 0,0078 0,0039 0,0020 0,0010 theorie-gem 0,0011 0,0003 0,0009-0,0070-0,0008-0,0001-0,0008 0,0000-0,0001-0,0002 relatieve fout (%) 0,22 0,12 0,73 11,16 2,61 0,55 10,42 1,21 4,31 16,12 relatieve fout bij 20 sim 0,35 0,26 0,80 0,34 0,68 3,37 6,34 9,37 16,04 1,54 relatieve fout bij 50 sim 0,27 0,07 0,44 0,30 0,88 1,93 4,01 7,94 9,33 10,08 Tabel 2: Resultaten simulatie M/M/1 rij Simulatietijd: interarrivaltijd: 2 bedieningstijd: 1 M/M/1-systeem In de tabel zijn de waardes voor de kans om een bepaalde populatie aan te treffen voor een M/M/1 systeem met een saturatiegraad van 0.5 weergegeven en vergeleken met de waarden die bekomen worden in de theorie. Er werden vijf simulaties gedaan, waarvoor bij elk de kans op de verschillende populaties berekend wordt. Dit wordt gedaan voor een populatie van 0 tot 9. De kans om een populatie aan te treffen van 10 of groter is kleiner dan 1/1000 en wordt verwaarloosd. In de derdelaatste rij wordt de relatieve fout op de populatiekans berekend met de simulatie tov. deze berekend met de theorie weergegeven. 57
58 In de voorlaatste rij staan de relatieve fouten bij een uitvoering van 20 simulaties en in de laatste rij de procentuele fout wanneer er 50 simulaties worden uitgevoerd. Hieruit blijkt dat de simulatieresultaten naar de resultaten uit de theorie convergeren. Dat in de laatste kolom de relatieve fout soms nog boven de 10% ligt is louter te wijten aan het feit dat de kans op deze populaties maar enkele duizenden is. De absolute afwijking bedraagt maar maximaal enkele tienduizendsten, wat zeer precies is Gemiddeld aantal wachtenden Het gemiddeld aantal wachtenden in de rij wordt verkregen als de som van de producten van de verschillende toestandskansen met hun bijhorende populatie; = k=0 N kpk wat herschreven kan worden tot N = ρ. 1 ρ Volgens de theorie is het gemiddeld aantal wachtenden 0,5 = ,5 Uit de simulatie volgt een gemiddelde populatie van De fout die gemaakt wordt is kleiner dan 2%, en dit reeds na vijf simulaties. Bij het doorlopen van 50 simulaties wordt er een gemiddelde wachtrijlengte van wagens berekend, een fout kleiner dan één procent. 58
59 De tijd gespendeerd in het systeem Verder kan men ook de gemiddelde tijd die een gebruiker in het systeem spendeert (T) berekenen. Uitgaande van de vergelijking van Little, N =λ x T [Little,1961]kan makkelijk worden berekend dat in het geval van een M/M/1-systeem T gegeven wordt door T= 1 µ 1 ρ Volgens de theorie spendeert elke gebruiker in het voorbeeld dus 2 tijdseenheden in het systeem. Uit het middelen van resultaten uit 5 simulaties (looptijd 10000) volgt een gemiddelde wachttijd van 1,987 wat een relatieve fout van iets meer dan een halve procent betekent. Het middelen van 50 simulaties met looptijd 200 levert een procentuele afwijking van 1 procent, maar gaat wel sneller Besluit M/M/1 De simulatie blijkt zeer nauwkeurige resultaten te geven bij een modellering als M/M/1- systeem. Hoe groter het aantal simulaties en de looptijd van de simulaties, hoe preciezer de resultaten worden. Dit heeft alles te maken met het stochastische karakter van de aankomst- en vertrekprocessen. Indien dit aantal groot genoeg wordt gekozen geeft de simulatie, afrondingsfouten niet te na gesproken, exacte resultaten weer. 59
60 4.1.2 Andere Markov-processen Analoge bewerkingen als voor de M/M/1 rij zijn ook uitgevoerd voor een M/M/m/, een M/D/1 een M/M/1/k en een M/M/m/m Markov wachtrijproces. Over deze resultaten kan algemeen gezegd worden dat ze ook allemaal de exacte oplossing benaderen. De convergentiesnelheid van de verschillende processen is hierbij functie van het aantal servers, en van de saturatiegraad. Hoe meer servers er aanwezig zijn, hoe trager de convergentie naar de exacte oplossing is. Bij lagere saturatiegraden stijgt de convergentiesnelheid. De kans om grotere populaties aan te treffen wordt dan al gauw zeer klein, waardoor er minder lange simulatietijden vereist zijn om toch al tot zeer goede benaderingen van het exacte resultaat te komen. Een gedetailleerde uitleg bij de verschillende berekeningen is toegevoegd in bijlage B: Andere markov-rijen Besluit simulatie van Markov-processen In het voorgaande deel werden de resultaten uit de simulatie van verschillende Markovprocessen weergegeven. Uit de voorbeelden komt duidelijk naar voor dat het programma op een zeer goede wijze de analytische formuleringen benadert. De enige afwijkingen ten overstaan van de theorie zijn een gevolg van afrondingsfouten, en van een te kort simulatieinterval. In het volgende deel zal nagegaan worden of met de simulatie even goed resultaten behaald worden wanneer reële verkeersprocessen gesimuleerd worden. Er zullen verschillende processen gesimuleerd worden waarna de resultaten vergeleken worden met de bestaand analytische en deterministische formuleringen. 60
61 4.2 Verkeerskundige processen In het vorige deel werd aangetoond dat het programma erin slaagt om op een exacte wijze een wijd spectrum aan Markov sterfte- en geboorteprocessen te simuleren. Hierbij werd tevens aangetoond dat de verschillende functies, om vertragingen en gemiddeld aantal gebruikers uit de simulatie te berekenen, ook correct functioneren. In dit deel wordt de overgang gemaakt naar meer realistische verkeerssituaties. Door gebruik te maken van een aaneenschakeling van verschillende wachtrijsystemen wordt geprobeerd om tot een goede benadering van de werkelijkheid te komen. Er wordt overgegaan op een meer expliciete simulatie. Zo worden de toeleveringen aan een bepaalde rij soms gebeuren door meerdere rijen. Hierdoor ontstaan netwerken van verkeerspatronen die vaak zeer moeilijk of niet meer analytisch te beschrijven zijn. In dit deel wordt de accuraatheid van het programma voor wat betreft het simuleren van reële verkeerssituaties gecontroleerd. Voor zowel kruisingen met als zonder verkeerslichten worden capaciteiten en vertragingen berekend. Deze resultaten worden vergeleken met gekende analytische formules. Omdat de werkelijkheid al snel te complex wordt, worden bij het opstellen van de analytische formuleringen aannames gemaakt. Vele van deze aannames zijn zeer redelijk en leveren goede resultaten. In verkeerssituaties waarbij de verkeersvraag tegen of boven het saturatieniveau ligt, schieten analytische formuleringen soms echter te kort. Het is net bij deze belastingen dat de sterkte van het programma zal blijken. Waar vertragingen berekend met de formules oneindig groot worden zal aangetoond worden dat de vertragingen berekend met het programma convergeren naar deterministisch bepaalde waarden. 61
62 4.2.1 Interactie tussen twee stromen aan kruispunten zonder verkeerslichten De eerste verkeerssituatie die beschouwd wordt is deze van een hoofdstroom die voorrang heeft op een tweede stroom. Deze tweede stroom wordt verder de zijstroom genoemd. Zowel de capaciteiten van de zijstroom in functie van het debiet van de hoofdstroom als de opgelopen vertragingen worden berekend. De resultaten die bekomen worden met de simulatie worden vergeleken met bestaande analytische formuleringen. Onder interacties wordt hier het proces van voorrang geven en voorrang nemen verstaan. De theorie houdt namelijk geen rekening met andere interacties zoals die zich bvb. voordoen wanneer een kruispunt klem komt te zitten. Hoewel ook deze interacties kunnen gesimuleerd worden is hiervoor dus echter geen referentiemateriaal uit de literatuur beschikbaar Capaciteit In de verkeersstudie zijn er voor deze situatie verschillende analytische formuleringen bekend die allen een goede benadering vormen voor de werkelijkheid. Deze formules geven de capaciteit van de zijstroom in functie van de capaciteit van de hoofdstroom. Hierbij wordt de distributie van de gaps in de hoofdstroom verondersteld exponentieel te zijn. De waarden voor de critical gap-tijd (T c ) en de follow-up tijd (T f ) worden constant verondersteld. De resultaten uit de simulatie worden vergeleken met de formuleringen 18 opgesteld door Drew, Buckley,Harders; e q. t q m = q p qp. t f 1 e P c door Siegloch ; q 1 q p. t c m =. e t f en door Tanner; q p.( tc tm ) q p. e q m = ( 1 q p. tm ). q p. t. f 1 e 18 In de formules staan q m,q p en q n respectievelijk voor de maximale intensiteit van de stroom die voorrang moet geven (de zijstroom), de intensiteit van de voorrangsstroom en de verkeersvraag van de zijstroom. 62
63 In de formules en de simulatie worden de kritische-gap tijd en de follow-up tijd respectievelijk gelijk genomen aan 6 en 3 seconden. De simulatie wordt uitgevoerd voor een range van verschillende intensiteiten van de hoofdstroom, en dit 10 maal per verschillende intensiteit. Hieruit wordt dan de gemiddelde intensiteit van de zijstroom horende bij de intensiteit van de hoofdstroom berekend. De resultaten worden weergegeven in tabel 3 en geplot in figuur 13. Intensiteit hoofdstroom (wagens/uur) Qm Harders ,6 1052,9 900,4 757,5 638,5 546,8 372,3 166,8 75,4 Qm Siegloch ,2 1010,7 828,9 671,9 551,0 464,1 313,7 162,4 104,1 Qm Tanner ,6 1054,7 907,9 774,0 665,2 583,0 430,6 256,9 180,3 Qm Simulatie Tabel 3: Vergelijking intensiteit uit simulatie met analytische formules Tijdsinterval 3600 Exponentieel verdeelde gaps In de tabel zijn de waarden weergegeven die verkregen worden wanneer de waardes voor de intensiteiten van de hoofdstroom uit de simulatie invullen in de respectievelijke formules voor de intensiteiten van de zijstroom. Uit deze tabel is duidelijk af te leiden dat de simulatie zeer aannemelijke resultaten oplevert. De simulatie geeft waardes voor de intensiteit van de zijstroom terug, die net iets boven de resultaten uit de formuleringen van Siegloch liggen, en een stukje onder de resultaten van Harders en Tanner. 63
64 Dit is ook goed te zien op onderstaande figuur, waarin q m uit de vergelijkingen van Harders, Siegloch en Tanner als een continue functie van q prior zijn geplot. Figuur 13: Vergelijking vertragingen simulatie, Harders, Siegloch en Tanner. T c =6sec en T f =3 sec. 64
65 4.2.2 Vertraging Vertragingen berekend met tijdsonafhanlijke formules De vertraging D die de wagens in de zijstroom oplopen, kan berekend worden met analytische, tijdsonafhankelijke formuleringen. Eén van deze formules is deze van Harders ; In de formule staat qn voor de verkeersvraag van de zijstroom, met name hoeveel wagens zich werkelijk aandienen in de zijstroom, terwijl qm voor het maximaal verwerkbaar verkeersvolume staat (zie eerder). Deze formule geeft goede resultaten, maar is maar beperkt bruikbaar. Ze geeft namelijk negatieve vertragingen wanneer de saturatiegraad hoger is als 1, dwz. wanneer q n groter is als q m. De formule is daarom enkel bruikbaar wanneer Op haar beurt is wordt naarmate q m echter ook weer beperkt, en dit door q p groter wordt, q m kleiner is als q n. q p. Zoals weergegeven in figuur 13 q m kleiner. Hierdoor daalt ook de maximaal toegestane q n om nog bruikbare resultaten te krijgen. Zo mag bvb. voor een intensiteit van de hoofdstroom van 1000 wagens per uur, de vraag van de zijstroom zeker niet groter zijn als 350 wagens per uur. Dit is weergegeven in figuur
66 Figuur 14: De gemiddelde vertraging in functie van de saturatiegraad volgens Harders Uit de figuur kan afgelezen worden dat wanneer we Qp een vaste waarde toekennen, bvb. 400 wagens per uur, dat dan vanaf een verkeersvraag van de zijstroom van 650 wagens per uur de berekende vertragingen exponentieel naar toegaan vanaf een saturatiegraad 0,8. De bruikbaarheid, zeker bij hoge saturatiegraden, van de analytische formules bij grote verkeersvraag van de zijstroom is dus begrensd. Wanneer we bovendien de waarde Qp nu laten toenemen van 400 tot 800 wagens per uur, dan blijkt deze exponentiële naar bij een saturatiegraad 0,8 zich al in te zetten bij een verkeersvraag van de zijstroom van ongeveer 370 wagens per uur. Het berekenen van vertragingen die in overeenstemming zijn met de werkelijkheid is bij grote intensiteit van zowel de hoofd- als de zijstroom is daarom niet mogelijk met de analytische formules. Ze zijn immers opgesteld voor een tijdsinterval met lengte gaande naar oneindig. In situaties met hoge belastingsgraden worden dan inderdaad uiterst grote gemiddelde vertragingen opgetekend. In de werkelijkheid hebben deze periodes van hoge belasting steeds een beperkte lengte. Er is dus nood aan formules die ook rekening houden met de lengte van het beschouwde tijdsinterval. 66
67 Bij een saturatiegraad 1 gaat de gemiddelde vertraging, berekend met analytische, tijdsonafhankelijke formuleringen zoals de formule van Harders naar oneindig. De resultaten die de simulatie weergeeft kunnen met de bestaande analytische formules vergeleken worden indien de saturatiegraden niet te hoog worden. De lengte van het beschouwde tijdsinterval heeft dan immers geen invloed op de gemiddelde vertraging. Voor veel hogere saturatiegraden (vanaf ρ = 2) zijn deterministische formuleringen bekend. Tussen deze kleine en grote saturatiegraden in gaat de gemiddelde vertraging van de tijdsonafhankelijke formules asymptotisch naar de deterministische formuleringen toe. Bij lage saturatiegraden moeten de resultaten uit de simulatie een sterke correlatie vertonen met de resultaten uit de analytische berekeningen. Voor saturatiegraden van 0,05 tot 0,9 zijn in onderstaande tabel de verschillende vertragingen berekend met de simulatie samengevat. Aangezien deze resultaten vergeleken worden met een vertragingsformule van Harders, wordt om q m te berekenen ook de capaciteitsformules van Harders gebruikt. In tabel 4 is de intensiteit van de hoofdstroom gelijk genomen aan 600 voertuigen per uur. Dit resulteert in een q m van 561 voertuigen per uur. Indien q n 561/2 is de saturatiegraad gelijk aan 0,5. Voor elke saturatiegraad werd de simulatie 40 keer doorlopen, waarna de gemiddeldes werden berekend. Het beschouwde tijdsinterval is 3600 seconden. De resultaten zijn ter verduidelijking ook nog eens geplot in figuur
68 Saturatiegraad 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 Uit simulatie 7,3523 8,3738 7,9836 8, ,2637 9, , , ,6026 Uit formule 7,3270 7,6260 7,9587 8,3313 8,7520 9,2310 9, , ,1769 Saturatiegraad 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 Uit simulatie 15, , , , , , , , ,5703 Uit formule 13, , , , , , , , ,8959 Tabel 4: Vergelijking gemiddelde vertragingen uit simulatie met analytische formuleringen. Figuur 15: Vertraging in de zijstroom (sec) in functie van saturatiegraad/ Qp=600 wagens/uur 68
69 Er kan opgemerkt worden dat er vanaf een saturatiegraad 0,9 een loskoppeling is van de resultaten uit de simulatie, en de vertragingen berekend met de formule van Harders. Zoals eerder reeds opgemerkt is dit te wijten aan het feit dat het tijdsinterval dat in de simulatie beschouwd wordt eindig is. In tabel 5 zijn de standaarddeviaties horende bij de berekeningen weergegeven. Bij zeer kleine saturatiegraden is deze relatief groot. Door de kleine bezetting zijn er grote relatieve verschillen in het aantal aankomsten. Dit zorgt voor een grote schommeling op de resultaten. Vanaf een saturatiegraad 0,1 halveert deze standaarddeviatie. De schommelingen zijn op de resultaten zijn dan heel wat minder. Standaarddeviaties bij de berekeningen van de vertragingen Saturatiegraad Standaarddev Saturatiegraad Standaarddev Saturatiegraad Standaarddev Saturatiegraad Standaarddev Tabel 5: Standaarddeviaties bij berekening van de vertragingen 69
70 Formules berekend met tijdsafhankelijke berekeningen Met toenemende saturatiegraden blijken de resultaten uit de simulatie minder en minder aan te sluiten bij de analytische berekeningen. Dit uit zich overduidelijk rond het punt met saturatiegraad 1. Op basis van de analytische uitdrukkingen kan in dit punt een oneindig grote vertraging verwacht worden. Dit blijkt echter niet het geval. Voor grotere saturatiegraden zijn andere, benaderende deterministische formules opgesteld. De volgende is er één van [TRB] ; Waarbij x d : de saturatiegraad D min : de minimale vertraging die men aan het kruispunt kan hebben. L 0 : de wachtrijlengte op tijdstip 0. T : de lengte van het interval waarin deze oversaturatie zich voordoet. q m : de maximale capaciteit van de zijstroom. De gemiddelde vertraging blijkt hier dus ook afhankelijk van de lengte van het interval waarvoor overcapaciteit zich voordoet. Hoe groter dit interval, hoe groter de gemiddelde vertragingen worden. In figuur 16 is deze vergelijking, samen met de resultaten uit de simulatie geplot voor T=360 en T=720 seconden. Per saturatiegraad zijn 10 simulaties uitgevoerd. Zoals op de figuur ook te zien is, is de overgang van tijdsonafhankelijke naar tijdsafhankelijke situaties niet strikt afgelijnd. In tabel 6 zijn de standaarddeviaties op de berekeningen gegeven. 70
71 Figuur 16: vergelijking vertragingen deterministische formulering en simulatie Standaarddeviaties bij de berekeningen van de vertragingen Saturatiegraad Std 720 sec Std 360 sec Saturatiegraad Std 720 sec Std 360 sec Saturatiegraad Std 720 sec Std 360 sec Saturatiegraad Std 720 sec Std 360 sec Saturatiegraad Std 720 sec Std 360 sec Saturatiegraad Std 720 sec Std 360 sec Tabel 6: Standaarddeviaties op de resultaten 71
72 De resultaten uit de simulatie blijken te oscilleren rond deze twee verschillende rechten. Deze oscillatie is natuurlijk het gevolg van het stochastische karakter. Ze zullen kleiner worden naarmate men meer simulaties laat lopen. Dit is natuurlijk een heel goed resultaat. Waar de analytische formuleringen tekort schieten en oneindig grote vertragingen voorspellen, beginnen de resultaten van de simulatie hiervan af te wijken en gaan asymptotisch naar deterministische formuleringen toe. Er kan besloten worden dat de simulatie, voor wat kruispunten zonder verkeerslichten betreft, de realiteit zeer goed benadert. In de volgende paragraaf zal nagegaan worden hoe de resultaten van de simulatie zijn op kruispunten met verkeerslichten Vertragingen aan kruispunten met verkeerslichten Bij kruispunten met verkeerslichten kan ook nagegaan worden wat de gemiddelde vertragingen zijn. Ook is het interessant te controleren of de simulatie realistische resultaten geeft voor het schatten van wachtrijlengtes. Zoals eerder reeds uiteengezet, wordt de interactie tussen stromen op kruispuntvlakken met verkeerslichten verwaarloosd. De theorie stelt geen capaciteitsformules op, omdat die toch makkelijk te berekenen is indien de totale groentijd binnen het beschouwde interval en de afrijcapaciteit bij groen licht gekend zijn. Het is namelijk hun product. Later tonen we aan dat dit toch niet persé altijd zo hoeft te zijn, maar eerst worden de prestaties van het programma voor het berekenen van de vertragingen aan kruispunten met verkeerslichten nagegaan. Net zoals in het vorige deel, zijn ook hier de vertragingen afhankelijk van de saturatiegraad. De saturatiegraad is nu te berekenen als x=(q/s)/(g/c). Hierbij is c de cyclustijd, g de effectieve groentijd, q het aantal wagens dat per tijdseenheid aankomt, en S het aantal wagens dat per tijdseenheid kan vertrekken tijdens de groenfase. Wanneer het rood is wordt de intensiteit van uitrijden gelijk aan nul. 72
73 Bij lage saturatiegraden kan weer een beroep gedaan worden op analytische formules, zoals de formules van Webster [Webester, 1958] of Miller [Miller, 1972] ; Q 0 staat hier voor de gemiddelde overloop van de wachtrij. Het is het gemiddelde aantal auto s dat nog voor het verkeerslicht staat als het licht weer op rood springt. Saturatiegraad 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Webster Miller Simulatie Tabel 7: Vergelijking vertragingen uit simulatie met analytische formules (kruispunt met verkeerslichten). In tabel 7 zijn de gemiddelde vertragingen (looptijd 3600 seconden, simulaties per saturatiegraad: 20) getabellariseerd, berekend met de formule van Webster, Miller, en met de simulatie. Bij saturatiegraden tot 0,8 is er weer een zeer goede overeenkomst tussen de resultaten. Bij hogere saturatiegraden stijgen de verwachte vertragingen berekend met analytische formules plots enorm om bij een saturatiegraad 1 een oneindige verwachte vertraging te geven. De resultaten hebben dus ongeveer hetzelfde patroon als bij kruipunten zonder verkeerslichten. De simulatie geeft ook een toegenomen stijgingsgraad weer voor de vertragingen vanaf het saturatiepunt, maar de verwachte vertragingen blijven toch nog beperkt in vergelijking met deze die verwacht worden met de analytische formuleringen. De curve van de gemiddelde vertragingen uit de simulatie gaat namelijk zeker niet naar oneindig. 73
74 De simulatie geeft bij hogere saturatiegraden weerom een veel realistischer resultaat dan de analytische formules aangezien vertragingen in de werkelijkheid nooit naar oneindig kunnen gaan. Voor hogere saturatiegraden zijn er weer deterministische formuleringen bekend. Akçelik [Akçelik, 1988] heeft een formule opgesteld die de deterministische formuleringen, die goede resultaten geven bij hoge saturatiegraden, en de analytische formuleringen die nauwkeuriger zijn bij lage saturatiegraden, verenigt. Om een goede overgang te bekomen tussen deze twee, maakt hij gebruik van de coördinaten-transformatiemethode. waarbij d de gemiddelde vertraging is. Figuur 17: Vertragingen volgens Akçelik, Webster, Miller en de simulatie 74
75 Uit figuur 17 blijkt weer dat de resultaten van de simulatie zeer dicht bij de werkelijkheid aanliggen. Er werden 20 simulaties per saturatiegraad 19 gemaakt. Het beschouwde tijdsinterval is 720 seconden. Al de resultaten uit de verschillende verificaties voor wat betreft de vertragingen zijn dus zeer goed gebleken. Ook op kruispunten met verkeerslichten blijkt de simuilatie niet alleen beter te doen als zuiver wiskundige analytische formules, weerom wordt de werkelijkheid zeer goed benaderd. De standaarddeviaties zijn gelijkaardig met die uit tabel 6. Tot slot kunnen ook nog de capaciteiten die men op een kruispunt met verkeerslichten zal hebben berekenen. Dit wordt gedaan voor een vaste saturatiegraad 0,8. In de figuur worden de vertragingen van de verschillende auto s uitgezet. Ook worden de vertrek- en aankomsttijden getekend. Op figuur 18 is duidelijk te zien dat tijdens rood licht er geen wagens de wachtrij meer uitrijden. De vertreklijn blijft daar horizontaal 20. Tijdens de rood lichtfase zien we de individuele vertragingen aangroeien, tijdens groen licht worden ze weer kleiner en vallen ze zelfs bijna terug tot nul. Figuur 18: Tekening van aankomst- en vertrekprocessen met bijhorende vertragingen 19 De saturatiegraad neemt met stappen van 0,05 toe van 0,05 tot De lijn van de vertrekken loopt lichtjes naar boven, maar dit is te wijten aan hoe Matlab verschillende vectoren ten overstaan van elkaar plot, en is geenszins een fout in de berekeningen. 75
76 Zowel de groen- als de roodfase duren 10 tijdseenheden. Er wordt gemiddeld 1 wagen aangeleverd per tijdseenheid, terwijl er tijdens de groenfase gemiddeld 2,5 wagens per tijdseenheid vertrekken. De saturatiegraad is dus 0,8. De vertrekken kennen een constante verdeling. Bij de aankomsten wordt er een onderscheid gemaakt tussen exponentiele of constante distributies. Net zoals de verkeerstheorie al verwachtte zijn de vertragingen bij een exponentiele verdeling gemiddeld groter. (vgl M/M/1 M/D/1 Markov-systemen) De schuin oplopende grafieken 21 geven de tijd van aankomst en van vertrek weer. Deze tijd kan worden afgelezen worden op de x-as. Op de y-as kan dan worden afgelezen worden het hoeveelste vertrek of aankomst het betreft. De onderste grafiek tekent de vertraging voor elke wagen. Op de X-as kan dan afgelezen worden over de hoeveelste auto het gaat, de vertraging wordt dan afgelezen op de Y-as. Op de grafiek zijn duidelijk de groen- en de roodfase te onderscheiden. In de roodfase bouwt de rijlengte op, de vertragingen nemen toe, terwijl ze in de groenfase weer afbouwen. Afhankelijk van het beschouwde interval 22 ligt de berekende gemiddelde vertraging in het voorbeeld tussen de 4,9 en de 5,4 tijdseenheden. Met de formule van Webster wordt een vertraging van 5,12 berekend. 21 Het feit dat de grafieken bij een constante aankomstintensiteit toch ietwat onregelmatig verlopen heeft enkel te maken met hoe Matlab een grafiek tekent uitgaande van de gegevens. 22 De gemiddelde vertraging is immers de totale oppervlakte die zich onder de driehoekige vertragingen-perwagen-lijn bevindt gedeeld door het aantal wagens. Afhankelijk van waar er wordt gestart en gestopt wordt met meten vindt men een iets grotere of iets kleinere gemiddelde oppervlakte per wagen weer. 76
77 4.3 Besluit verificatie In dit deel werd het simulatieprogramma getoetst aan een groot aantal gekende formuleringen uit de wachtrij- en verkeerstheorie. Alle simulaties geven resultaten terug die zeer nauw aansluiten bij de gekende formuleringen. Daar waar de resultaten afwijken van de analytische formules, is het omdat deze formules zelf te kort schieten in het benaderen van de werkelijkheid. Zelfs in deze situaties geeft de simulatie resultaten terug die de werkelijkheid zeer goed benaderen. Het voorbije deel kan dan ook beschouwd worden als een sterke theoretische onderbouwing en staving van het simulatiemodel. In het volgende hoofdstuk wordt dit model gebruikt om een aantal verkeerssituaties verder uit te werken. Hierbij wordt de invloed van verschillende fenomenen van de verkeersafwikkeling op gemiddelde vertragingen en op capaciteiten met elkaar vergeleken. 77
78 5 Hoofdstuk Toepassing In de vorige hoofdstukken werden eerst de functionele vereisten voor het simulatiemodel gestipuleerd. Vervolgens werd uiteengezet hoe deze vereisten omgezet zijn in een computermodel en in het hoofdstuk Verificatie werd de werking van dit model geverifieerd aan de hand van verschillende gekende formules. In dit hoofdstuk gaan we aan de gekende theorie voorbij. In de bestaande verkeersmodellen wordt er immers geen rekening gehouden met de interacties 23 tussen verschillende verkeersstromen op het kruispuntvlak zelf. Ze veronderstellen dat, bij stijgende belastingsgraden, de som van alle intensiteiten van de stromen over het kruispuntvlak toeneemt om uiteindelijk begrensd te worden door een maximale waarde, de capaciteit. In dit hoofdstuk wordt er door gebruik te maken van de simulatie aangetoond dat deze veronderstellingen niet altijd juist zijn. Er wordt aangetoond dat er zich een daling in de hoeveelheid wagens die het kruispunt kan verwerken kan voordoen. Bij een stijgende totale verkeersvraag neemt de totale capaciteit van het kruispunt af. In plaats van naar een maximale capaciteit toe te lopen kent het kruispunt dan, net door de interacties tussen de verschillende verkeersstromen, een capaciteitsval 23 Wanneer in dit hoofdstuk over interacties gesproken wordt, wordt de hinder bedoeld die verschillende wachtrijen op elkaar uitoefenen omdat hun lengtes te zeer zijn toegenomen om nog een normale verkeersafwikkeling toe te laten. Een voorbeeld van zulk een interactie is het feit dat wagens, wanneer ze groen hebben, het kruispuntvlak niet op kunnen rijden omdat er nog wagens uit een andere stroom op staan. 78
79 5.1 Situatieschets De verkeerssituatie die in dit hoofdstuk beschouwd wordt is weergegeven in figuur 19. Ze kan beschouwd worden als een uitsnede van de verkeerssituatie aan de Kapucijnenvoer, een dubbel kruispunt in Leuven. Om de situatie overzichtelijk te houden zijn er echter enkele vereenvoudigingen en aannames gemaakt. Figuur 19: Omzetting plan Kapucijnenvoer naar schematische voorstelling In figuur 19 is er aangegeven hoe een grondplan van de Kapucijnenvoer schematiserend opgesplitst in een aantal fysische entiteiten. In dit hoofdstuk worden enkel de niet gearceerde gebieden beschouwd. Om de verschillende verkeersstromen over dit deel van het kruispunt te kunnen betrouwbaar te kunnen simuleren worden verscheidene van deze entiteiten nog eens opgesplitst. De uiteindelijke opsplitsing in wachtrijen die ingegeven wordt in de simulatie is geschetst in figuur
80 Figuur 20: Voorstelling van de wachtrijen zoals ze in de simulatie worden ingegeven Verschillende verkeersstromen In de situatie zijn er vier verschillende verkeersstromen te onderscheiden. Stroom , stroom 2-1, stroom en stroom De wagens die het kruispunt oprijden via rij 2 rijden via rij 1 het kruispunt weer af. De wagens in stroom verlaten het kruispuntvlak via rij 7. Hierbij wordt verondersteld dat de wagens in rijen 1 en 7 zich niet mengen, en dus geen interacties aangaan. Hetzelfde wordt verondersteld voor de wagens in rijen 4 en 8. Stroom 2-1 kruist het traject van de stromen en Wagens uit rijen 4 en 8 moeten voorrang geven aan de wagens uit rij 2. Er wordt verondersteld dat de wagens uit rijen 4 en 8 voorrang geven zolang wachtrij 2 groen licht heeft, en er bovendien ook nog wagens staan te wachten om te vertrekken. Hierdoor wordt de gap-acceptatie tijd van de wagens in rij 4 en 8 impliciet gelijk verondersteld aan de bedieningstijd van wachtrij 2. De follow-up tijd is de bedieningstijd van de respectievelijke wachtrijen 4 en 8. Indien men een andere gapacceptatie tijd zou willen modelleren moet beroep gedaan worden op de eerder besproken gap-acceptatie rij. 80
81 Vanaf wanneer de populatie in wachtrij 1 een bepaalde grootte bereikt ( hinderlengte ) zal de staart van rij 1 het de wagens uit rijen 4 en 8 bemoeilijken om het kruispunt af te rijden. De bedieningstijd van deze rijen verhoogt. De verhoogde bedieningstijd van rijen 4 en 8 blijft behouden zolang de lengte van rij 1 niet weer kleiner wordt dan de hinderlengte. We noemen deze hinder een eerste orde hinder. De rij die de hinder veroorzaakt (rij 1) is rechtstreeks betrokken bij het conflict. Een andere interactie kan optreden tussen de wagens van stroom en stroom Wanneer op een bepaald moment de maximale capaciteit van wachtrij 4 bereikt wordt, kunnen de wagens die rij 3 uitrijden niet meer vlot doorrijden tot in rij 4. Ze blijven staan in rij 10. Daardoor hinderen ze de wagens van stroom Uit rij 6, aan de verkeerslichten, kunnen nog enkele wagens uitrijden. Ze worden echter gehinderd door de wagens in rij 10. Hierdoor loopt rij 11 vol waardoor uiteindelijk de wagens in rij 6 het kruispuntvlak niet meer kunnen oprijden. Deze interactie noemen we een interactie van tweede orde omdat ze initieel veroorzaakt worden door rij 1. Rij 1 is echter maar onrechtstreeks (via rijen 4 en 10) bij het conflict betrokken. Op zijn beurt kan stroom ook de stroom hinderen. Wanneer rij 7 volledig is volgelopen, wordt via rij 12 het uitrijden van rij 3 bemoeilijkt Verkeerslichtenregeling Rijen 1, 2, 3, 6, 7 en 9 hebben een verkeerslicht. Alle verkeerslichten hebben een cycluslengte van 90 seconden. Rijen 2,3 en 1/7 krijgen allen samen groen. Rij 2 en 3 gedurende 45 seconden, terwijl rijen 1 en 7 enkel gedurende de eerste 35 seconden groen licht krijgen. Na 45 seconden staan alle lichten op rood. Daarna krijgen rijen 6 en 9 gedurende 45 seconden groen licht, terwijl de andere rijen rood licht hebben. Deze verkeerslichtenregeling wijkt op twee plaatsen af van de regeling aan de Kapucijnenpoort; Ten eerste heeft rij 1 er langer groen. Rij 7 -aan de Kapucijnenpoort de wagens die af willen slaan- heeft er echter maar een twintigtal seconden groen. Op de Kapucijnenpoort wordt de hinder primair veroorzaakt door de stroom De rij die de belangrijkste bron van hinder is heeft er dus maar een beperkte groentijd. Rij 7 slaat terug op het kruispunt, waardoor rijen 4 en 8 gehinderd worden. 81
82 Ook het uitrijden van rij 2 wordt hierdoor gehinderd. In de situatie zoals ze hier wordt uitgewerkt wensen we het aantal interacties tot een overzichtelijk aantal te beperken. Daarom is er een vereenvoudigde situatie uitgewerkt waarbij de belangrijkste bron van hinder stroom 2-1 is. Daarom krijgt hier deze stroom maar een beperkte groentijd. Een tweede vereenvoudiging zit hem in het feit dat rijen 1 en 7 groen licht krijgen met stromen 2 en 3, in plaats van met stromen 6 en 9. De belangrijkste bron van problemen heeft op de Kapucijnenvoer groen licht samen met rijen 1 en 7. Aangezien deze bron nu stroom 2-1 is, wordt er hier verondersteld dat rij 2 (en daarbij rij 3) samen met rij 1 en 7 groen licht hebben, in plaats van stroom Er is in de uitwerking van de verkeerssituatie dus voor gekozen om de principiële werking van het kruispunt na te bootsen in plaats van de lichtenregeling letterlijk over te nemen. Hierdoor blijven de mechanismen van de interacties tussen de stromen ongeveer dezelfde, terwijl de situatie tegelijkertijd minder complex en overzichtelijker wordt Invloed van de verschillende stromen op elkaar Eerder werd al aangegeven dat de verschillende stromen een invloed op elkaar kunnen uitoefenen. Twee belangrijke parameters van deze invloed zijn ten eerste het aantal wagens in een wachtrij vooraleer deze een invloed uitoefent op een andere rij, en ten tweede de invloed zelf. Namelijk de nieuwe bedieningstijd voor de wagens in de rij die gehinderd wordt. Een gedetailleerd overzicht van alle eigenschappen van de verschillende rijen is toegevoegd in bijlage C: Eigenschappen van de wachtrijen in de toepassing. Naast de groentijden en de lichtcycli worden er ook de maximale capaciteit, de bedieningstijden, en de wijze van toelevering aangegeven. Indien toepasselijk zijn de hinderlengtes, en de verhoogde bedieningstijden ook vermeldt. 82
83 In het volgende deel wordt eerst nagegaan of er überhaupt wel een invloed is van deze interacties tussen de verschillende stromen op de verkeersafwikkeling en de capaciteit van het kruispunt. Daarna wordt de kwantitatieve invloed van de hinderlengte en de bedieningstijd bij hinder op deze capaciteit nagegaan. Natuurlijk zijn er nog vele andere parameters die elk hun invloed uitoefenen op het ontstaan, het evolueren en het oplossen van conflicten tussen stromen. Hierbij denken we bvb. aan de afstelling van de verkeerslichten, cycluslengtes, de verhouding tussen de intensiteiten tussen verschillende stromen op het kruispuntvlak, het aantal armen van het kruispunt, Een uitgebreide studie van de parameters, en een juiste kwantificering van hun invloed op de capaciteit van het kruispunt paste niet in het bestek van deze thesis, en wordt overgelaten voor uitgebreid verder onderzoek. 5.2 Berekeningen en resultaten In dit deel wordt de invloed van de interacties tussen verschillende stromen op de totale capaciteit van een kruispunt nagegaan. Hierbij wordt in stappen tewerk gegaan. In een eerste geval wordt er geen rekening gehouden met de invloed van interacties tussen de verschillende verkeersstromen. De resultaten die worden bekomen via deze werkwijze stemmen overeen met de resultaten die de huidige verkeersmodellen weergeven. Deze houden immers ook geen rekening met deze interacties. In een tweede stap wordt de hinder die wachtrij 1 uitoefent op de rijen 4 en 8 mee ingerekend. Uiteindelijk wordt er in een derde stap ook de hinder die de staart van rij 4 (via rij 10) uitoefent de stroom meegerekend. 83
84 5.2.1 Verwaarlozen van de interacties In dit deel worden de interacties tussen de verschillende stromen verwaarloosd. Er wordt dus verondersteld dat de lengte van wachtrij 1 geen invloed heeft op de afrijsnelheid van rijen 4 en 8. Natuurlijk moeten de wagens in deze stromen wel nog steeds voorrang verlenen aan de wagens die vanuit rij 2 naar rij 1 rijden. Zowel de intensiteiten van de verschillende stromen als de totale capaciteit van het hele kruispunt zijn berekend in functie van de verkeersvraag van rij 2 en rij Voor elke combinatie van een verkeersvraag van rij 2 en rij 3 zijn er 50 simulaties gedaan. In totaal werden er voor elke situatie dus 7x9x50=3150 simulaties uitgevoerd. Het beschouwde tijdsinterval is 720 seconden. De simulatie wordt uitgevoerd gedurende 840 seconden, maar de verkeersafwikkeling gedurende de eerste 120 seconden wordt niet meegerekend in de resultaten. Zo wordt de invloed van overgangsverschijnselen gematigd. In de onderstaande tabellen 8 tot 11 zijn de intensiteiten van de verschillende stromen in functie van de verschillende verkeersvragen weergegeven. In tabel 12 is de totale intensiteit over het kruispuntvlak getabellariseerd. Geen hinder Intensiteit Stroom 2-1 Verkeersvraag 25 rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 8: Intensiteit 2-1, geen hinder 24 De vraag verkeersvraag van rij 2 varieert van 100 tot 700 wagens per uur met stappen van 100. De opeenvolgende verkeersvragen van rij 3 zijn 100, 200, 250, 300, 350, 400, 500, 600 en 700 wagens per uur. 25 De aankomsten worden geloot uit een exponentiele verdeling met als gemiddelde, karakteristieke waarde de respectievelijke verkeersvragen per uur. Daarom kan het zijn dat in de tabel bij een bepaalde gemiddelde verkeersvraag de werkelijke intensiteit over het beschouwde traject toch groter is als deze gemiddelde verkeersvraag. De verkeersvraag moet dus beschouwd worden als een statistisch gemiddelde eerder dan als een werkelijke waarde. De intensiteit zou anders immers nooit hoger kunnen zijn dan de vraag. 84
85 Geen hinder Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 9: Intensiteit , geen hinder Geen hinder Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 10: Intensiteit 9-8-5, geen hinder 85
86 Geen hinder Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 11: Intensiteit , geen hinder Ook de totale intensiteit over het kruispunt wordt door de simulatie berekend. Deze moet natuurlijk gelijk 26 zijn aan de som van de intensiteiten van deze verschillende verkeersstromen apart. Geen hinder Totale Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 12: Totale intensiteit, geen hinder 26 De intensiteiten worden maar berekend voor een interval van 720 seconden. Om dus tot intensiteiten per uur te komen worden de resultaten met 5 vermenigvuldigd. Hierdoor kan de intensiteit per uur een kommagetal zijn. In de tabellen zijn de intensiteiten afgerond (naar beneden) tot op een eenheid. Door deze afrondingen kan het zijn dat de totale intensiteit iets groter is als de de som van de intensiteiten van de verschillende stromen uit de tabellen. 86
87 De standaarddeviaties op de berekening van de totale intensiteiten over het kruispunt worden weergegeven in tabel 13. Hoewel de simulaties maar een simulatie-interval van 720 seconden beschouwen worden de resultaten toch uitgezet in wagens per uur. Daarom moeten de berekende standaarddeviaties vermenigvuldigd worden met een factor Deze standaarddeviaties voor de totale intensiteit worden weergegeven in onderstaande tabel. De standaarddeviaties horende bij de intensiteiten van de verschillende stromen zijn getabellariseerd (tabelleriseerd 37-40) in bijlage D: Intensiteiten en standaarddeviaties bij de toepassing. Geen hinder Totale intens. Stand. dev. Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 13: Totale intensiteit, standaarddeviatie op berekeningen 27 De verwachtingswaarden van de intensiteiten worden lineair getransformeerd. De standaarddeviatie die berekend wordt in de simulatie moet dus ook aangepast worden. Uit de rekenregels voor de verwachtingsoperator, en uit de lineariteit van de integraaloperator volgt eenvoudig dat wanneer we de verwachtingswaarden vermenigvuldigen met een bepaalde waarde, dan we dan de standaarddeviatie van deze verwachtingswaarden moeten vermenigvuldigen met de absolute waarde van de waarde waarmee we de verwachtingswaarden vermenigvuldigden. Voor standaarddeviaties van steekproeven kunnen dezelfde rekenregels gehanteerd worden. [Beirlant en Van Dyck, 2001] 87
88 In onderstaande figuren 21 en 22 worden de resultaten van de berekeningen grafisch weergegeven. In figuur 21 zijn de totale intensiteiten horende bij de verschillende verkeersvragen van rij 2 en rij 3 weergegeven in een 3d-tekening 28. Het is de grafische weergave van tabel 12. Zoals reeds uit deze tabel kon afgelezen worden neemt de totale intensiteit van de verschillende stromen over het kruispunt toe met toenemende verkeersvraag van rij 2 en rij 3. Deze intensiteit gaat bij hogere verkeersvragen uiteindelijk naar een constante waarde toe. Dit is precies het resultaat dat we op basis van de literatuur zouden verwachten. Er is geen sprake van een capaciteitsval, en bij toenemende verkeersvraag wordt er uiteindelijk een maximale capaciteit van het kruispunt bereikt. Figuur 21: Totale intensiteit over het kruispunt in functie van verkeersvraag rij 2 en 3 Er kan opgemerkt worden dat een verkeersvraag van 1600 wagens per uur helemaal geen overdreven, onrealistische aanname is. Art Bleukx [Bleukx,2003] telde op de Kapucijnenvoer gedurende verschillende spitsperiodes in november 2002 een verkeersvraag tot wel 1800 pae per kwartier. Deze vraag werd natuurlijk wel verwerkt door het hele dubbelkruispunt. 28 Op de figuur zijn de X- en de Y-as weergegeven voor waardes van 0 tot 800. De tekening is echter maar geplot tot waardes 700. Door de ruimtelijke weergave zou hierdoor verwarring onnodige verwarring kunnen ontstaan. 88
89 Hoe de verschillende stromen bijdragen tot de totale intensiteit over het kruispunt is weergegeven in figuur 22. Hierbij wordt de verkeersvraag van rij 2 gevarieerd terwijl de verkeersvraag van rij 3 drie constant wordt gehouden aan 500 wagens/uur. Rond de totale intensiteit is een 95% betrouwbaarheidsinterval getekend. De boven en ondergrenzen worden gegeven door volgende formule 29 X z α 2 S n X + z, α 2 S n Hierbij is S de berekende standaarddeviatie van de steekproef (nl. de verschillende simulaties), n het aantal simulaties en X het gemiddelde van deze simulaties. Voor een 95% tweezijdig betrouwbaarheidsinterval is zijn weergegeven in tabel 14. z α gelijk aan 1,96. De resultaten van de berekeningen 2 Vraag rij Bovengrens Gemiddelde Ondergrens Tabel 14: Onder- en bovengrens 95% betrouwbaarheidsinterval tot. intensiteit, geen hinder 29 Hierbij wordt verondersteld dat de verschillende waardes voor de totale intensiteit over het kruispunt normaal verdeeld zijn rond de gemiddelde waarde. 89
90 Figuur 22: Aandeel stromen in totale intensiteit (geen hinder) In figuur 22 is goed te zien dat de variatie van de verkeersvraag van stroom 2 geen enkele invloed uitoefent op de intensiteit van de andere drie stromen. Hoewel de verkeersvraag van rij wagens per uur is, ligt de intensiteit maar net boven de 400 wagens per uur. Dit heeft te maken met het feit dat er nog andere beperkingen zijn op de intensiteit van stroom De bedieningstijd van het licht aan rij 3 is 4 seconden per wagen. Per uur passeren er dus maximaal 450 voorbij dit licht (het is immers maar de helft van de tijd groen licht). Ook de intensiteiten van stromen en variëren niet met veranderende verkeersvraag van rij 2. De intensiteit van stroom 2-1 daarentegen neemt eerst lineair toe volgens een 45 gradenlijn, waarna deze intensiteit bij hogere verkeersvraag afbuigt naar een constante waarde van ongeveer wagens per uur. Het feit dat de totale intensiteit over het kruispunt stijgt bij toenemende verkeersvraag, totdat ze uiteindelijk begrensd wordt door een maximale capaciteit van het kruispunt is precies wat analytische verkeersmodellen voorspellen. 30 Rij 1 heeft 35 seconden groen in een cyclus van 90 seconden. Per uur heeft deze rij dus 1400 seconden groen licht. De intensiteit waarmee bij groen licht de wagens de rij verlaten is exponentieel verdeeld rond met een gemiddelde waarde van 0,25 wagens per seconde. Per uur passeren er dus gemiddeld 350 wagens langs rij 1, tenzij dat de verkeersvraag natuurlijk kleiner is als deze waarde. 90
91 In de volgende paragraaf wordt nagegaan wat de invloed van de interacties tussen verkeersstromen op het kruispunt is op de intensiteiten van deze verschillende verkeersstromen en op de totale capaciteit van het kruispunt Inrekenen van interacties tussen stromen In dit deel wordt nagegaan wat de invloed is van de interacties tussen stromen op hun respectievelijke intensiteiten, en op de totale intensiteit van het hele kruispunt. De interacties die we beschouwen kunnen opgesplitst worden in een interactie van eerste en van tweede orde. Op dit kruispunt ligt stroom 2-1 aan de basis van de problemen. Bij hoge verkeersvragen wordt de staart van rij 1 zo lang, dat deze de wagens in rijen 4 en 8 zal hinderen bij het afrijden van het kruispunt. Deze interactie tussen de staart van rij 1, en de rijen 4 en 8 noemen we in deze paragraaf de hinder van eerste orde. Door deze hinder neemt de bedieningstijd van rij 4 toe. Hierdoor komen er meer wagens toe in rij 4 dan er door rij 4 verwerkt kunnen worden. De staart van rij 4 groeit aan, en wordt op zijn beurt oorzaak van een hinder. Stroom hindert dan de vlotte doorstroming van stroom Omdat dit effect ook, maar niet rechtstreeks, gevolg is van een te lange wachtrij 1, noemen we dit een effect van tweede orde. Dit betekent echter niet dat de invloed van deze hinder minder groot moet zijn. In een eerste deel wordt alleen de hinder van eerste orde in ogenschouw genomen. Nadien worden dan alle interacties meegerekend Eerste orde hinder Door het inrekenen van de interacties tussen de verkeersstromen gaan we aan de theoretische benadering van verkeersafwikkeling op kruispunten voorbij. De literatuur houdt hier namelijk geen rekening mee. We nemen aan dat de staart van rij 1 de rijen 4 en 8 hindert vanaf dat er zich 8 wagens in rij 1 bevinden. Door deze hinder neemt de bedieningstijd van beide rijen toe tot 25 seconden per wagen. Door deze toename relatief groot te veronderstellen wordt de invloed van de interacties uitvergroot. 91
92 Verder in de tekst wordt zowel de invloed van de grootte van deze bedieningstijd, als het aantal wagens dat zich in wachtrij 1 moet bevinden vooraleer er hinder optreedt 31 bestudeerd. Weer wordt er een interval van 720 seconden beschouwd. Voor elke combinatie van de onafhankelijk van elkaar veranderende verkeersvragen van rij 2 en rij 3 worden er 50 simulaties uitgevoerd. 1 e ordehinder Intensiteit 2-1 Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 15: Intensiteit 2-1, 1 e orde hinder 1 e ordehinder Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 16: Intensiteit 2-1, 1 e orde hinder 31 Verder in de tekst wordt er naar dit aantal wagens vooraleer er hinder optreedt ook verwezen met de term hinderlengte. 92
93 1 e ordehinder Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 17: Intensiteit 9-8-5, 1 e orde hinder 1 e ordehinder Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 18: Intensiteit 9-8-5, 1 e orde hinder 93
94 1 e ordehinder Totale Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 19: Totale intensiteit, 1 e orde hinder In tabel 20 bevinden zich de standaarddeviaties horende bij de totale intensiteiten. Doordat er nu meer interacties -die elk stochastisch benaderd worden- ingerekend worden, wordt de onzekerheid op de resultaten groter. Dit vertaalt zich in grotere standaarddeviaties. De standaarddeviaties op de intensiteiten van de verschillende stromen apart zijn weergegeven in bijlage D (tabellen 40 tot 44). 1 e ordehinder Tot. intens. Stand. dev. Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 20: Standaarddeviatie bij totale intensiteit, 1 e orde hinder 94
95 Uit tabel 19 (totale intensiteiten) is af te lezen dat wanneer de verkeersvraag van rij 2 stijgt van 300 naar 400 wagens per uur, dat er dan een daling is in de capaciteit van het kruispunt. Er is sprake van een capaciteitsval, een capacity-drop! Bestaande formules houden hier geen rekening mee, waardoor ze in bepaalde gevallen grote overschattingen maken van de capaciteit van het kruispunt. De totale intensiteit van alle stromen op het kruispunt wordt grafisch weergegeven in figuur 23. Figuur 23: totale intensiteit in functie van verkeersvraag rij 2 en 3 (eerste orde hinder ingerekend) Om een duidelijkere weergave mogelijk te maken is de richting van de as met de verkeersvraag van rij 2 van veranderd. Op de tekening is duidelijk te zien dat wanneer de verkeersvraag van rij 3 constant wordt gehouden, dat de totale capaciteit van het kruispunt dan eerst toeneemt bij toenemende verkeersvraag van rij 2. Wanneer de verkeersvraag van rij 2 echter blijft toenemen, doet er zich een capaciteitsval voor; Bij een toenemende verkeersvraag worden er minder wagens verwerkt door het kruispunt. 95
96 In de tabel 21 is de verhouding tussen aantal wagens dat het kruispunt per uur verwerkt bij een bepaalde verkeersvraag van rij 2, ten opzichte van een verkeersvraag van 300 wagens per uur van rij 2 gegeven. Uit de tabel kan afgelezen worden dat het kruispunt bij een verdubbeling van de verkeersvraag van rij 2, van 300 naar 600 wagens per uur, 20% minder wagens verwerkt. Verkeersvraag Rij 2 (wagens/uur) Intensitei t Intensiteit max Tabel 21: verhouding intensiteit tot maximale intensiteit, 1 e orde hinder Er dient er belangrijk onderscheid gemaakt te worden tussen het aantal wagens dat het kruispunt verwerkt bij een verkeersvraag kleiner of groter dan 300. Wanneer de verkeersvraag van rij 2 kleiner is als 300, dan verwerkt het kruispunt niet meer wagens omdat er zich niet meer wagens aandienen. De marginale totale intensiteit in functie van de verkeersvraag van rij Intensiteitkruispunt 2 is positief; VerkeersvraagRij 2 > 0 Wanneer er zich meer wagens aandienen in wachtrij 2, dan neemt de totale intensiteit van het kruispunt toe. De capaciteit van het kruispunt kent ergens een maximale waarde in functie van de verkeersvraag van rij 2. Wanneer de verkeersvraag van rij 2 vanuit deze waarde nog blijft toenemen, dan neemt het aantal wagens dat het kruispunt kan verwerken af. De intensiteit van de stromen over het kruispunt is dan tevens gelijk aan de capaciteit van het kruispunt. De capaciteit van het kruispunt daalt, er is een capaciteitsval. In dit geval geldt; Intensiteitkruispunt VerkeersvraagRij 2 < 0. De capaciteit van het kruispunt neemt af tot een waarde die kleiner is dan de maximale capaciteit van het kruispunt. Verder wordt aangetoond dat deze waarde bvb. afhangt van de bedieningstijd die verondersteld wordt indien er zich hinder voordoet. 96
97 In figuur 24 zijn de bijdrages van de intensiteiten van de verschillende stromen tot de totale intensiteit van het kruispunt weergegeven. Hiertoe is er een uitsnede genomen uit de 3Dfiguur, waarbij de verkeersvraag van rij 2 constant gehouden wordt op 500 wagens per uur. Ook is er een 95% betrouwbaarheidsinterval van de totale intensiteit op het kruispunt getekend. Figuur 24: Aandeel stromen in totale intensiteit (1 e orde hinder) In de figuur is goed te zien dat de verkeersvraag van rij 2 nog steeds geen invloed heeft op de intensiteit van stroom Zowel rij 4 als rij 8 kunnen nu echter wel gehinderd worden door de staart van rij 1. We zien dat de intensiteit van beide stromen afneemt wanneer de verkeersvraag van rij 3 groter wordt. Vanaf een verkeersvraag van rij 2 van 500 wagens per uur blijven de intensiteiten ongeveer constant. Zo gaat de capaciteit van het kruispunt na de val ook naar een constante waarde toe. 97
98 De grenzen van het 95% betrouwbaarheidsinterval worden op exact dezelfde wijze als eerder berekend. Ze worden hieronder nog eens even in een tabelvorm (tabel 22) weergegeven. Vraag rij Bovengrens Gemiddelde Ondergrens Tabel 22: Onder- en bovengrens 95% betrouwbaarheidsinterval tot. intensiteit, 1 e orde hinder In deze paragraaf werd aangetoond dat er zich ook op kruispunten effectief een capaciteitsval kan voordoen, de totale intensiteit over het kruispunt neemt af bij een toenemende verkeersvraag. In volgende paragraaf wordt bestudeerd hoe de intensiteit van de verschillende stromen verloopt indien ook de tweede orde interactie tussen stroom en stroom wordt ingerekend Eerste en tweede orde hinder In dit deel wordt nu ook de tweede orde interactie, de invloed die stroom uitoefent op stroom meegerekend. De totale intensiteit in functie van de verkeersvraag van rijen 2 en 3 wordt weergegeven in tabel
99 1 e en 2 e orde Hinder Totale Intensiteit Verkeersvraag rij 2 (wagens/uur) Verkeersvraag rij 3 (wagens/uur) Tabel 23: Totale intensiteit; 1 e en 2 e orde hinder Figuur 25: totale intensiteit in functie van verkeersvraag rij 2 en 3 (1 e en 2 e orde hinder) In figuur 25 zijn de resultaten van de berekeningen ruimtelijk weergegeven. De vorm van de 3D figuur verandert niet zo veel in vergelijking met de vorige situatie. Wanneer we de verkeersvraag van rij 3 constant houden, krijgen we bij lage verkeersvraag van rij 2 weer een stijgend verloop voor de totale intensiteit over het kruipunt. 99
Memo. Inleiding. Onderwerp: Memo doorstroming rotonde Parklaan Zandlaan - Horalaan
 Memo Onderwerp: Memo doorstroming rotonde Parklaan Zandlaan - Horalaan Kampen, Projectomschrijving: 30 november 2018 Simulatie rotonde Parklaan Zandlaan Horalaan. Van: BonoTraffics bv, Opgesteld door:
Memo Onderwerp: Memo doorstroming rotonde Parklaan Zandlaan - Horalaan Kampen, Projectomschrijving: 30 november 2018 Simulatie rotonde Parklaan Zandlaan Horalaan. Van: BonoTraffics bv, Opgesteld door:
Kantoorruimte is simpelweg te duur om verloren te laten gaan aan ongebruikte toiletten technische studie Kurt Van Hautegem Wouter Rogiest
 Kantoorruimte is simpelweg te duur om verloren te laten gaan aan ongebruikte toiletten technische studie Kurt Van Hautegem Wouter Rogiest In dit document geven we een korte toelichting bij de aannames
Kantoorruimte is simpelweg te duur om verloren te laten gaan aan ongebruikte toiletten technische studie Kurt Van Hautegem Wouter Rogiest In dit document geven we een korte toelichting bij de aannames
AUTORIJSCHOOL JOHN VAN DEN KIEBOOM VLAMINGVAART 49 4651 GR STEENBERGEN
 Op het examen worden natuurlijk wel eens fouten gemaakt. In de loop der jaren hebben wij al verschillende fouten gezien en daarom hebben wij besloten deze fouten, samen met enkele tips, op papier te zetten.
Op het examen worden natuurlijk wel eens fouten gemaakt. In de loop der jaren hebben wij al verschillende fouten gezien en daarom hebben wij besloten deze fouten, samen met enkele tips, op papier te zetten.
Figuur 1. Schematisch overzicht van de structuur van het twee-stadia recourse model.
 Samenvatting In dit proefschrift worden planningsproblemen op het gebied van routering en roostering bestudeerd met behulp van wiskundige modellen en (numerieke) optimalisatie. Kenmerkend voor de bestudeerde
Samenvatting In dit proefschrift worden planningsproblemen op het gebied van routering en roostering bestudeerd met behulp van wiskundige modellen en (numerieke) optimalisatie. Kenmerkend voor de bestudeerde
Verificatie en calibratie MaDAM
 Verificatie en calibratie MaDAM Remco van Thiel Graduation Date: 15 October 2004 Graduation committee: v. Berkum Weijermars Birnie Organisation: Goudappel Coffeng Inleiding Het wordt steeds drukker op
Verificatie en calibratie MaDAM Remco van Thiel Graduation Date: 15 October 2004 Graduation committee: v. Berkum Weijermars Birnie Organisation: Goudappel Coffeng Inleiding Het wordt steeds drukker op
DHR. S. VAN DONKELAAR (VAN RIEZEN & PARTNERS) J.HAVEMAN (BVA VERKEERSADVIEZEN) ONDERWERP ONTSLUITING MEET INN DATUM 29 AUGUSTUS 2016
 Kantoorcomplex Paris Noordzeelaan 38-A 8017 JW Zwolle postbus 40089 8004 DB Zwolle T (038) 460 6747 bva@bvaverkeer.nl www.bvaverkeer.nl AAN VAN DHR. S. VAN DONKELAAR (VAN RIEZEN & PARTNERS) J.HAVEMAN (BVA
Kantoorcomplex Paris Noordzeelaan 38-A 8017 JW Zwolle postbus 40089 8004 DB Zwolle T (038) 460 6747 bva@bvaverkeer.nl www.bvaverkeer.nl AAN VAN DHR. S. VAN DONKELAAR (VAN RIEZEN & PARTNERS) J.HAVEMAN (BVA
Case Simulink EE4- Building a SSV - Team PM1 21 maart 2014
 Case Simulink EE4- Building a SSV - Team PM1 21 maart 2014 Inhoudsopgave Inhoudsopgave... 1 Figurenlijst... 1 Inleiding... 2 Gedrag van het zonnepaneel gekoppeld aan een weerstand... 2 Gedrag van de DC-motor
Case Simulink EE4- Building a SSV - Team PM1 21 maart 2014 Inhoudsopgave Inhoudsopgave... 1 Figurenlijst... 1 Inleiding... 2 Gedrag van het zonnepaneel gekoppeld aan een weerstand... 2 Gedrag van de DC-motor
Summary in Dutch 179
 Samenvatting Een belangrijke reden voor het uitvoeren van marktonderzoek is het proberen te achterhalen wat de wensen en ideeën van consumenten zijn met betrekking tot een produkt. De conjuncte analyse
Samenvatting Een belangrijke reden voor het uitvoeren van marktonderzoek is het proberen te achterhalen wat de wensen en ideeën van consumenten zijn met betrekking tot een produkt. De conjuncte analyse
Kennisdeling in lerende netwerken
 Kennisdeling in lerende netwerken Managementsamenvatting Dit rapport presenteert een onderzoek naar kennisdeling. Kennis neemt in de samenleving een steeds belangrijker plaats in. Individuen en/of groepen
Kennisdeling in lerende netwerken Managementsamenvatting Dit rapport presenteert een onderzoek naar kennisdeling. Kennis neemt in de samenleving een steeds belangrijker plaats in. Individuen en/of groepen
Notitie. Referentienummer Datum Kenmerk 10 december Betreft Simulatie Herenweg Nollenweg
 Notitie Datum Kenmerk 10 december 2013 332356 Betreft Simulatie Herenweg Nollenweg In 2012 hebben Provinciale Staten het Uitvoeringsprogramma Visie OV 2020 vastgesteld. Een van de deelprogramma s is het
Notitie Datum Kenmerk 10 december 2013 332356 Betreft Simulatie Herenweg Nollenweg In 2012 hebben Provinciale Staten het Uitvoeringsprogramma Visie OV 2020 vastgesteld. Een van de deelprogramma s is het
Fiche Leerlingen. De plaats op de openbare weg binnen de bebouwde kom
 De plaats op de openbare weg binnen de bebouwde kom Kijk naar de fietsers. Kleur de nummers van de fietsers die de verkeersregels volgen en op de juiste plaats rijden groen. Kleur de nummers van de fietsers
De plaats op de openbare weg binnen de bebouwde kom Kijk naar de fietsers. Kleur de nummers van de fietsers die de verkeersregels volgen en op de juiste plaats rijden groen. Kleur de nummers van de fietsers
Een kruispunt. is geen jungle
 Een kruispunt is geen jungle Bebouwde kommen bevatten allerhande kruispunten waar verschillende types weggebruikers elkaar ontmoeten. Door de drukte en de verscheidenheid van het verkeer is het gevaar
Een kruispunt is geen jungle Bebouwde kommen bevatten allerhande kruispunten waar verschillende types weggebruikers elkaar ontmoeten. Door de drukte en de verscheidenheid van het verkeer is het gevaar
Files overal ook in de computer! Dr. Sven Maerivoet
 Files overal ook in de computer! Dr. Sven Maerivoet 21 Sven September Maerivoet Internationaal 2012 Internationaal Wiskundetoernooi Wiskundetoernooi 2012 2012 1 Overzicht. Transport- en verkeersmodellering
Files overal ook in de computer! Dr. Sven Maerivoet 21 Sven September Maerivoet Internationaal 2012 Internationaal Wiskundetoernooi Wiskundetoernooi 2012 2012 1 Overzicht. Transport- en verkeersmodellering
doe-fiche fietser Opstappen en wegrijden uw kind politie Bilzen - Hoeselt - Riemst nog niet kiest de dichtsbijzijnde plaats waar de rit kan beginnen.
 Opstappen en wegrijden 7 kiest de dichtsbijzijnde plaats waar de rit kan beginnen. kijkt uit hoe het veilig en zonder het verkeer te hinderen de startplaats kan bereiken. stapt met de fiets aan de hand
Opstappen en wegrijden 7 kiest de dichtsbijzijnde plaats waar de rit kan beginnen. kijkt uit hoe het veilig en zonder het verkeer te hinderen de startplaats kan bereiken. stapt met de fiets aan de hand
Werkdocument Hotel t Koningsbed Versie 16 mei 2012
 Werkdocument Hotel t Koningsbed Versie 16 mei 2012 1 Inleiding 1.1 Achtergrond Hotel Het Koningsbed is gelegen aan de Prinsenlaan te Groenekan. Het is een van oorsprong agrarisch bedrijf, waar enkele jaren
Werkdocument Hotel t Koningsbed Versie 16 mei 2012 1 Inleiding 1.1 Achtergrond Hotel Het Koningsbed is gelegen aan de Prinsenlaan te Groenekan. Het is een van oorsprong agrarisch bedrijf, waar enkele jaren
Beleving van wachten bij verkeerslichten
 (Bijdragenr. 129) Beleving van wachten bij verkeerslichten Jaap Vreeswijk Peek Traffic bv Bas van der Bijl Grontmij (voorheen stagiair bij Peek Traffic bv) Korte samenvatting De wachttijdbeleving van automobilisten
(Bijdragenr. 129) Beleving van wachten bij verkeerslichten Jaap Vreeswijk Peek Traffic bv Bas van der Bijl Grontmij (voorheen stagiair bij Peek Traffic bv) Korte samenvatting De wachttijdbeleving van automobilisten
Waarom wachten voor verkeerslichten? Inhoud 2/16/2010. Introductie Wachtrijtheorie Simpel model: een opengebroken weg
 Waarom wachten voor verkeerslichten? Marko Boon Nationale Wiskunde Dagen 2010 Inhoud Introductie Simpel model: een opengebroken weg Met vaste afstellingen Met dynamische afstellingen Ingewikkeldere kruispunten
Waarom wachten voor verkeerslichten? Marko Boon Nationale Wiskunde Dagen 2010 Inhoud Introductie Simpel model: een opengebroken weg Met vaste afstellingen Met dynamische afstellingen Ingewikkeldere kruispunten
De hoofdstuknummers in deze bundel corresponderen met de hoofdstukken in het diktaat 1 VERKEERSSTROOMTHEORIE OF: HOE ONTSTAAN FILES?
 CTB1420 Oefenopgaven Deel 4 - Antwoorden De hoofdstuknummers in deze bundel corresponderen met de hoofdstukken in het diktaat 1 VERKEERSSTROOMTHEORIE OF: HOE ONTSTAAN FILES? 1. Eenheden a) Dichtheid: k,
CTB1420 Oefenopgaven Deel 4 - Antwoorden De hoofdstuknummers in deze bundel corresponderen met de hoofdstukken in het diktaat 1 VERKEERSSTROOMTHEORIE OF: HOE ONTSTAAN FILES? 1. Eenheden a) Dichtheid: k,
Modelleren en simuleren van verkeersstromen
 Modelleren en simuleren van verkeersstromen Sven Maerivoet Maart 2003 Waar zal het over gaan? De nadruk zal liggen op : modelleren en simuleren We hebben het dus niet over : verkeersbeheersing 2 Overzicht
Modelleren en simuleren van verkeersstromen Sven Maerivoet Maart 2003 Waar zal het over gaan? De nadruk zal liggen op : modelleren en simuleren We hebben het dus niet over : verkeersbeheersing 2 Overzicht
CURRICULUM PRAKTIJKOPLEIDING CATEGORIE B
 CURRICULUM PRAKTIJKOPLEIDING CATEGORIE B INLEIDING Het Curriculum Praktijkopleiding Categorie B bundelt de essentiële kennis, vaardigheden en gedragsaspecten die een leerling tijdens de praktijkopleiding
CURRICULUM PRAKTIJKOPLEIDING CATEGORIE B INLEIDING Het Curriculum Praktijkopleiding Categorie B bundelt de essentiële kennis, vaardigheden en gedragsaspecten die een leerling tijdens de praktijkopleiding
Deze brochure frist je kennis op van deze op het eerste gezicht vanzelfsprekende, maar o zo noodzakelijke regels. Een kruispunt is immers geen jungle!
 Een k is geeruispunt n jung le Bebouwde kommen bevatten allerhande kruispunten waar verschillende types weggebruikers elkaar ontmoeten. Door de drukte en de verscheidenheid van het verkeer is het gevaar
Een k is geeruispunt n jung le Bebouwde kommen bevatten allerhande kruispunten waar verschillende types weggebruikers elkaar ontmoeten. Door de drukte en de verscheidenheid van het verkeer is het gevaar
Wachten in de supermarkt
 Wachten in de supermarkt Rik Schepens 0772841 Rob Wu 0787817 22 juni 2012 Begeleider: Marko Boon Modelleren A Vakcode: 2WH01 Inhoudsopgave Samenvatting 1 1 Inleiding 1 2 Theorie 1 3 Model 3 4 Resultaten
Wachten in de supermarkt Rik Schepens 0772841 Rob Wu 0787817 22 juni 2012 Begeleider: Marko Boon Modelleren A Vakcode: 2WH01 Inhoudsopgave Samenvatting 1 1 Inleiding 1 2 Theorie 1 3 Model 3 4 Resultaten
De dynamica van een hertenpopulatie. Verslag 1 Modellen en Simulatie
 De dynamica van een hertenpopulatie Verslag Modellen en Simulatie 8 februari 04 Inleiding Om de groei van een populatie te beschrijven, kunnen vele verschillende modellen worden gebruikt, en welke meer
De dynamica van een hertenpopulatie Verslag Modellen en Simulatie 8 februari 04 Inleiding Om de groei van een populatie te beschrijven, kunnen vele verschillende modellen worden gebruikt, en welke meer
EverGreen: minder stoppen, betere luchtkwaliteit, maar
 (Bijdragenr. 70) EverGreen: minder stoppen, betere luchtkwaliteit, maar A. Bezemer (DTV Consultants) C. Stolz (DTV Consultants) J.G.M. Boormans (DTV Consultants) K. Langelaar (DTV Consultants) Samenvatting
(Bijdragenr. 70) EverGreen: minder stoppen, betere luchtkwaliteit, maar A. Bezemer (DTV Consultants) C. Stolz (DTV Consultants) J.G.M. Boormans (DTV Consultants) K. Langelaar (DTV Consultants) Samenvatting
Fout van CPB bij berekening remgeldeffect eigen risico
 Fout van CPB bij berekening remgeldeffect eigen risico Wynand van de Ven en Erik Schut Wederreactie op Douven en Mannaerts In ons artikel in TPEdigitaal (Van de Ven en Schut 2010) hebben wij uiteengezet
Fout van CPB bij berekening remgeldeffect eigen risico Wynand van de Ven en Erik Schut Wederreactie op Douven en Mannaerts In ons artikel in TPEdigitaal (Van de Ven en Schut 2010) hebben wij uiteengezet
Nieuwe rekenmethode (voertuigafhankelijke) verkeerslichtenregelingen
 Nieuwe rekenmethode (voertuigafhankelijke) verkeerslichtenregelingen Carl Stolz DTV Consultants Bart Veroude DTV Consultants Samenvatting In dit paper worden delen van een nieuwe methode voor het doorrekenen
Nieuwe rekenmethode (voertuigafhankelijke) verkeerslichtenregelingen Carl Stolz DTV Consultants Bart Veroude DTV Consultants Samenvatting In dit paper worden delen van een nieuwe methode voor het doorrekenen
(Bijdragenr. 82) Dynamisch voetgangersmodel
 (Bijdragenr. 82) Dynamisch voetgangersmodel Willem J. Mak Teun Immerman (Vialis bv) 1. Waarom voetgangersmodellen Door de komst van de microsimulatiemodellen is het al een aantal jaren mogelijk om complexe
(Bijdragenr. 82) Dynamisch voetgangersmodel Willem J. Mak Teun Immerman (Vialis bv) 1. Waarom voetgangersmodellen Door de komst van de microsimulatiemodellen is het al een aantal jaren mogelijk om complexe
Kruispunt 5: N340 Kranenburgweg Vechtdijk
 Kruispunt 5: N340 Kranenburgweg Vechtdijk Pagina 2 van 14 Inhoud Samenvatting kruispunt 5 5 5 Kruispunt 5: N340 Kranenburgweg Vechtdijk 7 5.1 Inleiding 7 5.2 Observaties 5.3 Analyse 7 8 5.4 Maatregelen
Kruispunt 5: N340 Kranenburgweg Vechtdijk Pagina 2 van 14 Inhoud Samenvatting kruispunt 5 5 5 Kruispunt 5: N340 Kranenburgweg Vechtdijk 7 5.1 Inleiding 7 5.2 Observaties 5.3 Analyse 7 8 5.4 Maatregelen
*** L E G E N D E. Moeilijkheidsgraad van het knooppunt: * niet echt moeilijk ** opletten geblazen *** ogen en oren wijd open!
 L E G E N D E *** Moeilijkheidsgraad van het knooppunt: * niet echt moeilijk ** opletten geblazen *** ogen en oren wijd open! Kijk naar, maak oogcontact met Linkerarm uitsteken Rechterarm uitsteken Fietstraject
L E G E N D E *** Moeilijkheidsgraad van het knooppunt: * niet echt moeilijk ** opletten geblazen *** ogen en oren wijd open! Kijk naar, maak oogcontact met Linkerarm uitsteken Rechterarm uitsteken Fietstraject
De Grote Verkeerstoets - 2014 07/08/2014. 1. Ja. 2. Neen, want ik mag hier niet links afslaan. 3. Neen, want ik heb mijn arm niet uitgestoken.
 100082: Welk voorwerp houd je hier boven je hoofd? 1. Een rood voorwerp. 2. Een map. 3. Een voetbal. 100081: Je slaat af naar links. Gebeurt dat hier helemaal veilig? 1. Ja. 2. Neen, want ik mag hier niet
100082: Welk voorwerp houd je hier boven je hoofd? 1. Een rood voorwerp. 2. Een map. 3. Een voetbal. 100081: Je slaat af naar links. Gebeurt dat hier helemaal veilig? 1. Ja. 2. Neen, want ik mag hier niet
BEOORDELINGSCRITERIA FIETSOVERSTEEK EIKENLAAN. Algemeen
 BEOORDELINGSCRITERIA FIETSOVERSTEEK EIKENLAAN Algemeen Met het uitvoeren van het monitoringsplan wordt het functioneren van de fietsoversteek in de verschillende situaties in beeld gebracht, namelijk in
BEOORDELINGSCRITERIA FIETSOVERSTEEK EIKENLAAN Algemeen Met het uitvoeren van het monitoringsplan wordt het functioneren van de fietsoversteek in de verschillende situaties in beeld gebracht, namelijk in
VERGELIJKENDE STUDIE VAN ALTERNATIEVE ONTWERPWAARDE SCHATTINGEN VAN SIGNIFICANTE GOLFHOOGTE
 Rapport aan isterie van de Vlaamse Gemeenschap Departement Leefmilieu en Infrastructuur Administratie Waterwegen en Zeewezen AFDELING WATERWEGEN KUST VERGELIJKENDE STUDIE VAN ALTERNATIEVE ONTWERPWAARDE
Rapport aan isterie van de Vlaamse Gemeenschap Departement Leefmilieu en Infrastructuur Administratie Waterwegen en Zeewezen AFDELING WATERWEGEN KUST VERGELIJKENDE STUDIE VAN ALTERNATIEVE ONTWERPWAARDE
R-89-25 Ir. A. Dijkstra Leidschendam, 1989 Stichting Wetenschappelijk Onderzoek Verkeersveiligheid SWOV
 SCHEIDING VAN VERKEERSSOORTEN IN FLEVOLAND Begeleidende notitie bij het rapport van Th. Michels & E. Meijer. Scheiding van verkeerssoorten in Flevoland; criteria en prioriteitsstelling voor scheiding van
SCHEIDING VAN VERKEERSSOORTEN IN FLEVOLAND Begeleidende notitie bij het rapport van Th. Michels & E. Meijer. Scheiding van verkeerssoorten in Flevoland; criteria en prioriteitsstelling voor scheiding van
Manoeuvres en bewegingen, struikelblok bij theoretisch proefexamen op www.vabrijbewijs.be
 Manoeuvres en bewegingen, struikelblok bij theoretisch proefexamen op www.vabrijbewijs.be Dit is de belangrijkste conclusie van VAB-Rijschool die de resultaten evalueert van de 5000 laatst afgelegde proefexamens
Manoeuvres en bewegingen, struikelblok bij theoretisch proefexamen op www.vabrijbewijs.be Dit is de belangrijkste conclusie van VAB-Rijschool die de resultaten evalueert van de 5000 laatst afgelegde proefexamens
Populaties beschrijven met kansmodellen
 Populaties beschrijven met kansmodellen Prof. dr. Herman Callaert Deze tekst probeert, met voorbeelden, inzicht te geven in de manier waarop je in de statistiek populaties bestudeert. Dat doe je met kansmodellen.
Populaties beschrijven met kansmodellen Prof. dr. Herman Callaert Deze tekst probeert, met voorbeelden, inzicht te geven in de manier waarop je in de statistiek populaties bestudeert. Dat doe je met kansmodellen.
Transparantie in dynamische modellen voor wegverkeer
 Transparantie in dynamische modellen voor wegverkeer A model should be as simple as possible, but not simpler... (A. Einstein) PLATOS2011, 3/8/11 Dr. Hans van Lint Prof. Dr. Serge Hoogendoorn Delft University
Transparantie in dynamische modellen voor wegverkeer A model should be as simple as possible, but not simpler... (A. Einstein) PLATOS2011, 3/8/11 Dr. Hans van Lint Prof. Dr. Serge Hoogendoorn Delft University
Fysieke Activiteit bij 50-plussers. The Relationship between Self-efficacy, Intrinsic Motivation and. Physical Activity among Adults Aged over 50
 De relatie tussen eigen-effectiviteit 1 De Relatie tussen Eigen-effectiviteit, Intrinsieke Motivatie en Fysieke Activiteit bij 50-plussers The Relationship between Self-efficacy, Intrinsic Motivation and
De relatie tussen eigen-effectiviteit 1 De Relatie tussen Eigen-effectiviteit, Intrinsieke Motivatie en Fysieke Activiteit bij 50-plussers The Relationship between Self-efficacy, Intrinsic Motivation and
Docentenhandleiding Blok I3+I4 (H5+H6) Besturen en Regelen met de PC Reinder Jongsma
 Docentenhandleiding Blok I3+I4 (H5+H6) Besturen en Regelen met de PC Reinder Jongsma 1. Leerdoelen en subdoelen van het blok Leerdoelen Systematisch analyseren van een programma van eisen Doorgronden van
Docentenhandleiding Blok I3+I4 (H5+H6) Besturen en Regelen met de PC Reinder Jongsma 1. Leerdoelen en subdoelen van het blok Leerdoelen Systematisch analyseren van een programma van eisen Doorgronden van
Hoofdstuk 3: Cardiovasculaire toestandsveranderingen in gesimuleerde werkomgevingen
 Een inspirerende nieuwe fase in het onderzoek naar mens-computer interactie heeft zich aangediend met het ontstaan van adaptieve automatisering. Binnen dit onderzoeksgebied worden technologische systemen
Een inspirerende nieuwe fase in het onderzoek naar mens-computer interactie heeft zich aangediend met het ontstaan van adaptieve automatisering. Binnen dit onderzoeksgebied worden technologische systemen
Bespreking Examen Analyse 1 (Augustus 2007)
 Bespreking Examen Analyse 1 (Augustus 2007) Vooraf: Zoals het stilletjes aan een traditie is geworden, geef ik hier bedenkingen bij het examen van deze septemberzittijd. Ik zorg ervoor dat deze tekst op
Bespreking Examen Analyse 1 (Augustus 2007) Vooraf: Zoals het stilletjes aan een traditie is geworden, geef ik hier bedenkingen bij het examen van deze septemberzittijd. Ik zorg ervoor dat deze tekst op
Methoden voor simultane toegang tot en verkeersregulering in draadloze communicatienetwerken
 Samenvatting Methoden voor simultane toegang tot en verkeersregulering in draadloze communicatienetwerken De enorme toename in het gebruik van draadloze communicatienetwerken heeft geleid tot een sterk
Samenvatting Methoden voor simultane toegang tot en verkeersregulering in draadloze communicatienetwerken De enorme toename in het gebruik van draadloze communicatienetwerken heeft geleid tot een sterk
N237 Provincie Utrecht: MBO Systeem
 (Bijdragenr. 54) N237 Provincie Utrecht: MBO Systeem ir. Mark Snoek IT&T Samenvatting Het MBO Systeem van IT&T geeft tijdens de uitgebreide werkzaamheden aan de A28 de Provincie Utrecht inzicht in de realtime
(Bijdragenr. 54) N237 Provincie Utrecht: MBO Systeem ir. Mark Snoek IT&T Samenvatting Het MBO Systeem van IT&T geeft tijdens de uitgebreide werkzaamheden aan de A28 de Provincie Utrecht inzicht in de realtime
Kruispunt 1, 2 en 3: Aansluiting N307 - A50
 Kruispunt 1, 2 en 3: Aansluiting N307 - A50 A50 A50 Inhoud Samenvatting kruispunt 1, 2 en 3 5 1 Kruispunt 1, 2 en 3 7 1.1 Inleiding 7 1.2 Observaties 1.3 Analyse 8 9 1.4 Maatregelen 11 1.5 Kosten 11 Bijlage
Kruispunt 1, 2 en 3: Aansluiting N307 - A50 A50 A50 Inhoud Samenvatting kruispunt 1, 2 en 3 5 1 Kruispunt 1, 2 en 3 7 1.1 Inleiding 7 1.2 Observaties 1.3 Analyse 8 9 1.4 Maatregelen 11 1.5 Kosten 11 Bijlage
1. Soorten wetenschappelijke informatiebronnen
 1. Soorten wetenschappelijke informatiebronnen Wanneer je als student in het hoger onderwijs de opdracht krijgt om te zoeken naar wetenschappelijke informatie heb je de keuze uit verschillende informatiebronnen.
1. Soorten wetenschappelijke informatiebronnen Wanneer je als student in het hoger onderwijs de opdracht krijgt om te zoeken naar wetenschappelijke informatie heb je de keuze uit verschillende informatiebronnen.
Antwoorden Kennisvragenlijst voorrangsvoertuigen
 Antwoorden Kennisvragenlijst voorrangsvoertuigen Wet- en regelgeving 1. Wanneer ben je bestuurder van een voorrangsvoertuig? (bron: artikel 29 RVV 1990) a. als je optische én geluidssignalen voert b. als
Antwoorden Kennisvragenlijst voorrangsvoertuigen Wet- en regelgeving 1. Wanneer ben je bestuurder van een voorrangsvoertuig? (bron: artikel 29 RVV 1990) a. als je optische én geluidssignalen voert b. als
Voorrang hebben versus overschrijding van de maximumsnelheid
 Voorrang hebben versus overschrijding van de maximumsnelheid Mr. Bert Kabel (1) Inleiding In het hedendaagse verkeer komt het regelmatig voor dat verkeersdeelnemers elkaar geen voorrang verlenen. Gelukkig
Voorrang hebben versus overschrijding van de maximumsnelheid Mr. Bert Kabel (1) Inleiding In het hedendaagse verkeer komt het regelmatig voor dat verkeersdeelnemers elkaar geen voorrang verlenen. Gelukkig
Het Verband Tussen Persoonlijkheid, Stress en Coping. The Relation Between Personality, Stress and Coping
 Het Verband Tussen Persoonlijkheid, Stress en Coping The Relation Between Personality, Stress and Coping J.R.M. de Vos Oktober 2009 1e begeleider: Mw. Dr. T. Houtmans 2e begeleider: Mw. Dr. K. Proost Faculteit
Het Verband Tussen Persoonlijkheid, Stress en Coping The Relation Between Personality, Stress and Coping J.R.M. de Vos Oktober 2009 1e begeleider: Mw. Dr. T. Houtmans 2e begeleider: Mw. Dr. K. Proost Faculteit
Gemeente Enschede. Verkeersafwikkelingsstudie Zuiderval Resultaten aanvullende simulaties
 Gemeente Enschede Verkeersafwikkelingsstudie Zuiderval Resultaten aanvullende simulaties Gemeente Enschede Verkeersafwikkelingsstudie Zuiderval Resultaten aanvullende simulaties Datum 6 november 29 ESD131/Bsm/1362
Gemeente Enschede Verkeersafwikkelingsstudie Zuiderval Resultaten aanvullende simulaties Gemeente Enschede Verkeersafwikkelingsstudie Zuiderval Resultaten aanvullende simulaties Datum 6 november 29 ESD131/Bsm/1362
Exponentiële Functie: Toepassingen
 Exponentiële Functie: Toepassingen 1 Overgang tussen exponentiële functies en lineaire functies Wanneer we werken met de exponentiële functie is deze niet altijd gemakkelijk te herkennen. Daarom proberen
Exponentiële Functie: Toepassingen 1 Overgang tussen exponentiële functies en lineaire functies Wanneer we werken met de exponentiële functie is deze niet altijd gemakkelijk te herkennen. Daarom proberen
EWMA Control Charts in Statistical Process Monitoring I.M. Zwetsloot
 EWMA Control Charts in Statistical Process Monitoring I.M. Zwetsloot EWMA Control Charts in Statistical Process Monitoring Inez M. Zwetsloot Samenvatting EWMA Regelkaarten in Statistische Procesmonitoring
EWMA Control Charts in Statistical Process Monitoring I.M. Zwetsloot EWMA Control Charts in Statistical Process Monitoring Inez M. Zwetsloot Samenvatting EWMA Regelkaarten in Statistische Procesmonitoring
1. Een stilstaand voertuig voorbijrijden 2. Rechts een weg inslaan
 Hoe moeten de fietstaken uitgevoerd worden? 1. Een stilstaand voertuig voorbijrijden 2. Rechts een weg inslaan mindert snelheid en kijkt voor zich uit. kijkt om : nadert er verkeer? vertraagt of versnelt,
Hoe moeten de fietstaken uitgevoerd worden? 1. Een stilstaand voertuig voorbijrijden 2. Rechts een weg inslaan mindert snelheid en kijkt voor zich uit. kijkt om : nadert er verkeer? vertraagt of versnelt,
Website Performance Rapport 2013: E-COMMERCE
 Website Performance Rapport 2013: E-COMMERCE E-commerce sites behoren als categorie tot de sites met de slechtste performance, ondanks het feit dat beschikbaarheid en performance rechtstreeks impact hebben
Website Performance Rapport 2013: E-COMMERCE E-commerce sites behoren als categorie tot de sites met de slechtste performance, ondanks het feit dat beschikbaarheid en performance rechtstreeks impact hebben
Bijdragenr. 32. Verkeerskundig beheer van verkeerslichten en andere verkeerssystemen
 Bijdragenr. 32 Verkeerskundig beheer van verkeerslichten en andere verkeerssystemen ****** Erna Schol (Rijkswaterstaat Dienst Verkeer en Scheepvaart, Groene Golf Team) Emile Oostenbrink (CROW) Samenvatting
Bijdragenr. 32 Verkeerskundig beheer van verkeerslichten en andere verkeerssystemen ****** Erna Schol (Rijkswaterstaat Dienst Verkeer en Scheepvaart, Groene Golf Team) Emile Oostenbrink (CROW) Samenvatting
Gegevensverwerving en verwerking
 Gegevensverwerving en verwerking Staalname - aantal stalen/replicaten - grootte staal - apparatuur Experimentele setup Bibliotheek Statistiek - beschrijvend - variantie-analyse - correlatie - regressie
Gegevensverwerving en verwerking Staalname - aantal stalen/replicaten - grootte staal - apparatuur Experimentele setup Bibliotheek Statistiek - beschrijvend - variantie-analyse - correlatie - regressie
HANDLEIDING ANALYSE FINANCIËLE EFFECTEN VERVOERSSYSTEMEN
 HANDLEIDING ANALYSE FINANCIËLE EFFECTEN VERVOERSSYSTEMEN 2010 Policy Research Corporation, namens de sociale partners inhet beroepsgoederenvervoer over de weg en de logistiek (CNV, FNV, TLN en VVT) Meer
HANDLEIDING ANALYSE FINANCIËLE EFFECTEN VERVOERSSYSTEMEN 2010 Policy Research Corporation, namens de sociale partners inhet beroepsgoederenvervoer over de weg en de logistiek (CNV, FNV, TLN en VVT) Meer
ZICHTBAARHEID EN VISUELE GELEIDING VOOR WEGGEBRUIKERS
 ZICHTBAARHEID EN VISUELE GELEIDING VOOR WEGGEBRUIKERS Verslag van het Symposium "Providing visibility and visual guidance to the road user", Washington, D.C., 30 juli - 1 augustus 1984. Artikel Verkeerskunde
ZICHTBAARHEID EN VISUELE GELEIDING VOOR WEGGEBRUIKERS Verslag van het Symposium "Providing visibility and visual guidance to the road user", Washington, D.C., 30 juli - 1 augustus 1984. Artikel Verkeerskunde
360 FEEDBACK 15/06/2012. Thomas Leiderschap Vragenlijst. Thomas Voorbeeld. Persoonlijk & Vertrouwelijk
 360 FEEDBACK 15/06/2012 Thomas Leiderschap Vragenlijst Thomas Voorbeeld Persoonlijk & Vertrouwelijk S Hamilton-Gill & Thomas International Limited 1998-2013 http://www.thomasinternational.net 1 Inhoud
360 FEEDBACK 15/06/2012 Thomas Leiderschap Vragenlijst Thomas Voorbeeld Persoonlijk & Vertrouwelijk S Hamilton-Gill & Thomas International Limited 1998-2013 http://www.thomasinternational.net 1 Inhoud
Inhoud. Introductie tot de cursus
 Inhoud Introductie tot de cursus 1 Inleiding 7 2 Voorkennis 7 3 Het cursusmateriaal 7 4 Structuur, symbolen en taalgebruik 8 5 De cursus bestuderen 9 6 Studiebegeleiding 10 7 Huiswerkopgaven 10 8 Het tentamen
Inhoud Introductie tot de cursus 1 Inleiding 7 2 Voorkennis 7 3 Het cursusmateriaal 7 4 Structuur, symbolen en taalgebruik 8 5 De cursus bestuderen 9 6 Studiebegeleiding 10 7 Huiswerkopgaven 10 8 Het tentamen
De Relatie tussen Angst en Psychologische Inflexibiliteit. The Relationship between Anxiety and Psychological Inflexibility.
 RELATIE ANGST EN PSYCHOLOGISCHE INFLEXIBILITEIT 1 De Relatie tussen Angst en Psychologische Inflexibiliteit The Relationship between Anxiety and Psychological Inflexibility Jos Kooy Eerste begeleider Tweede
RELATIE ANGST EN PSYCHOLOGISCHE INFLEXIBILITEIT 1 De Relatie tussen Angst en Psychologische Inflexibiliteit The Relationship between Anxiety and Psychological Inflexibility Jos Kooy Eerste begeleider Tweede
Verkeersafwikkeling. 2e Hogeweg Onderzoek noodzaakbepaling VRl's twee kruispunten. Opdrachtgever. Opdrachtnemer
 Verkeersafwikkeling 2e Hogeweg Onderzoek noodzaakbepaling VRl's twee kruispunten Opdrachtgever Opdrachtnemer Naam: Gemeente Zeist Afdeling: Realisatie & Beheer Postbus 513 3700 AM Zeist DTV Consultants
Verkeersafwikkeling 2e Hogeweg Onderzoek noodzaakbepaling VRl's twee kruispunten Opdrachtgever Opdrachtnemer Naam: Gemeente Zeist Afdeling: Realisatie & Beheer Postbus 513 3700 AM Zeist DTV Consultants
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Woensdag 25 mei totale examentijd 3 uur
 wiskunde A1 Examen VWO - Compex Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Woensdag 25 mei totale examentijd 3 uur 20 05 Vragen 1 tot en met 13 In dit deel staan de vragen waarbij de computer niet
wiskunde A1 Examen VWO - Compex Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Woensdag 25 mei totale examentijd 3 uur 20 05 Vragen 1 tot en met 13 In dit deel staan de vragen waarbij de computer niet
Folkert Buiter 2 oktober 2015
 1 Nuchter kijken naar feiten en trends van aardbevingen in Groningen. Een versneld stijgende lijn van het aantal en de kracht van aardbevingen in Groningen. Hoe je ook naar de feitelijke metingen van de
1 Nuchter kijken naar feiten en trends van aardbevingen in Groningen. Een versneld stijgende lijn van het aantal en de kracht van aardbevingen in Groningen. Hoe je ook naar de feitelijke metingen van de
Hoofdstuk 20 Wachtrijentheorie
 Hoofdstuk 20 Wachtrijentheorie Beschrijving Iedereen van ons heeft al tijd gespendeerd in een wachtrij: b.v. aanschuiven in de Alma restaurants. In dit hoofdstuk onwikkelen we mathematische modellen voor
Hoofdstuk 20 Wachtrijentheorie Beschrijving Iedereen van ons heeft al tijd gespendeerd in een wachtrij: b.v. aanschuiven in de Alma restaurants. In dit hoofdstuk onwikkelen we mathematische modellen voor
We zullen in deze les kijken hoe we netwerken kunnen analyseren, om bijvoorbeeld de volgende vragen te kunnen beantwoorden:
 Wiskunde voor kunstmatige intelligentie, 24 Les 5 Proces analyse Veel processen laten zich door netwerken beschrijven, waarin een aantal knopen acties aangeeft en opdrachten langs verbindingen tussen de
Wiskunde voor kunstmatige intelligentie, 24 Les 5 Proces analyse Veel processen laten zich door netwerken beschrijven, waarin een aantal knopen acties aangeeft en opdrachten langs verbindingen tussen de
Examen H 111 Datum: vrijdag 9 juni 2000 Tijd: uur
 Examen H 111 Datum: vrijdag 9 juni 2000 Tijd: 10.00 13.00 uur Katholieke Universiteit Leuven Departement Burgerlijke Bouwkunde Instructies: Er zijn 5 vragen; Start de beantwoording van elk van de 5 vragen
Examen H 111 Datum: vrijdag 9 juni 2000 Tijd: 10.00 13.00 uur Katholieke Universiteit Leuven Departement Burgerlijke Bouwkunde Instructies: Er zijn 5 vragen; Start de beantwoording van elk van de 5 vragen
We illustreren deze werkwijze opnieuw a.h.v. de steekproef van de geboortegewichten
 Hoofdstuk 8 Betrouwbaarheidsintervallen In het vorige hoofdstuk lieten we zien hoe het mogelijk is om over een ongekende karakteristiek van een populatie hypothesen te formuleren. Een andere manier van
Hoofdstuk 8 Betrouwbaarheidsintervallen In het vorige hoofdstuk lieten we zien hoe het mogelijk is om over een ongekende karakteristiek van een populatie hypothesen te formuleren. Een andere manier van
Overgangsverschijnselen
 Hoofdstuk 5 Overgangsverschijnselen Doelstellingen 1. Overgangsverschijnselen van RC en RL ketens kunnen uitleggen waarbij de wiskundige afleiding van ondergeschikt belang is Als we een condensator of
Hoofdstuk 5 Overgangsverschijnselen Doelstellingen 1. Overgangsverschijnselen van RC en RL ketens kunnen uitleggen waarbij de wiskundige afleiding van ondergeschikt belang is Als we een condensator of
Ontwerp kruispunten. Verkeerslichtengeregelde kruispunten. zijn geen kruispunten met verkeerslichten
 Ontwerp kruispunten Verkeerslichtengeregelde kruispunten zijn geen kruispunten met verkeerslichten Basisbegrippen Voorbeelden lantaarns volle lens 3-kleurig voetgangerslicht pijllicht voorlooppijl tramlicht
Ontwerp kruispunten Verkeerslichtengeregelde kruispunten zijn geen kruispunten met verkeerslichten Basisbegrippen Voorbeelden lantaarns volle lens 3-kleurig voetgangerslicht pijllicht voorlooppijl tramlicht
Verkeersmodel op maat: sneller en beter
 Verkeersmodel op maat: sneller en beter Door veel meer data naar veel betere antwoorden Wim van der Hoeven Nationaal Verkeerskunde Congres Nieuwegein, 2 november 2011 Situatie In Nederland relatief veel
Verkeersmodel op maat: sneller en beter Door veel meer data naar veel betere antwoorden Wim van der Hoeven Nationaal Verkeerskunde Congres Nieuwegein, 2 november 2011 Situatie In Nederland relatief veel
De Relatie Tussen de Gehanteerde Copingstijl en Pesten op het Werk. The Relation Between the Used Coping Style and Bullying at Work.
 De Relatie Tussen de Gehanteerde Copingstijl en Pesten op het Werk The Relation Between the Used Coping Style and Bullying at Work Merijn Daerden Studentnummer: 850225144 Werkstuk: Empirisch afstudeeronderzoek:
De Relatie Tussen de Gehanteerde Copingstijl en Pesten op het Werk The Relation Between the Used Coping Style and Bullying at Work Merijn Daerden Studentnummer: 850225144 Werkstuk: Empirisch afstudeeronderzoek:
Waterweerstand. 1 Inleiding. VWO Bovenbouwpracticum Natuurkunde Practicumhandleiding
 VWO Bovenbouwpracticum Natuurkunde Practicumhandleiding Waterweerstand 1 Inleiding Een bewegend vaartuig ondervindt altijd weerstand van het langsstromende water: het water oefent een wrijvingskracht uit
VWO Bovenbouwpracticum Natuurkunde Practicumhandleiding Waterweerstand 1 Inleiding Een bewegend vaartuig ondervindt altijd weerstand van het langsstromende water: het water oefent een wrijvingskracht uit
Leidt de maatregel rechtsaf door rood (RADR) voor fietsers tot een toename van roodrijden elders?
 Leidt de maatregel rechtsaf door rood (RADR) voor fietsers tot een toename van roodrijden elders? Tim De Ceunynck Instituut voor Mobiliteit (IMOB) - Universiteit Hasselt tim.deceunynck@uhasselt.be Inleiding
Leidt de maatregel rechtsaf door rood (RADR) voor fietsers tot een toename van roodrijden elders? Tim De Ceunynck Instituut voor Mobiliteit (IMOB) - Universiteit Hasselt tim.deceunynck@uhasselt.be Inleiding
De actuariële aspecten van het nieuw prudentieel kader voor IBP s. Verband tussen het nieuw prudentieel kader en de actuariële praktijken
 De actuariële aspecten van het nieuw prudentieel kader voor IBP s Verband tussen het nieuw prudentieel kader en de actuariële praktijken 6 december 2007 1 Verband tussen het nieuw prudentieel kader en
De actuariële aspecten van het nieuw prudentieel kader voor IBP s Verband tussen het nieuw prudentieel kader en de actuariële praktijken 6 december 2007 1 Verband tussen het nieuw prudentieel kader en
EFFECTIVENESS OF MATH LEARNING IN THE FIRST YEARS OF SPECIAL PRIMARY EDUCATION a Propensity Score Matching Approach
 EFFECTIVENESS OF MATH LEARNING IN THE FIRST YEARS OF SPECIAL PRIMARY EDUCATION a Propensity Score Matching Approach Gudrun Vanlaar, Machteld Vandecandelaere, Jan Van Damme, Bieke De Fraine & Katja Petry
EFFECTIVENESS OF MATH LEARNING IN THE FIRST YEARS OF SPECIAL PRIMARY EDUCATION a Propensity Score Matching Approach Gudrun Vanlaar, Machteld Vandecandelaere, Jan Van Damme, Bieke De Fraine & Katja Petry
Theorieles groep 5/6
 Theorieles groep 5/6 Alles op een rij voor de leerkracht van groep 5/6 Met dit document kunt u een theorieles over het onderwerp verkeersveiligheid geven aan de groepen 5 en 6. Deze theorieles bestaat
Theorieles groep 5/6 Alles op een rij voor de leerkracht van groep 5/6 Met dit document kunt u een theorieles over het onderwerp verkeersveiligheid geven aan de groepen 5 en 6. Deze theorieles bestaat
HOOFDSTUK 6: INTRODUCTIE IN STATISTISCHE GEVOLGTREKKINGEN
 HOOFDSTUK 6: INTRODUCTIE IN STATISTISCHE GEVOLGTREKKINGEN Inleiding Statistische gevolgtrekkingen (statistical inference) gaan over het trekken van conclusies over een populatie op basis van steekproefdata.
HOOFDSTUK 6: INTRODUCTIE IN STATISTISCHE GEVOLGTREKKINGEN Inleiding Statistische gevolgtrekkingen (statistical inference) gaan over het trekken van conclusies over een populatie op basis van steekproefdata.
B e r e k e n i n g v e r k e e r s t o e d e l i n g e n p a r k e e r b e h o e f t e W e- r e l d b a z a r t e W i n s c h o t e n
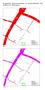 B e r e k e n i n g v e r k e e r s t o e d e l i n g e n p a r k e e r b e h o e f t e W e- r e l d b a z a r t e W i n s c h o t e n figuur 1 f i g u u r 2 V e r k e e r s t o e d e l i n g I n l e i
B e r e k e n i n g v e r k e e r s t o e d e l i n g e n p a r k e e r b e h o e f t e W e- r e l d b a z a r t e W i n s c h o t e n figuur 1 f i g u u r 2 V e r k e e r s t o e d e l i n g I n l e i
Beheer en onderhoud. 4 onafhankelijke onderzoeken: 1. Federal Highway Administration. 2. Low Cost Measures. 3. Warnke Studie. 4.
 Beheer en onderhoud 4 onafhankelijke onderzoeken: 1. Federal Highway Administration (US Department of Transportation, Verenigde Staten) 2. Low Cost Measures (Elsamex Spanje) 3. Warnke Studie (Deutsche
Beheer en onderhoud 4 onafhankelijke onderzoeken: 1. Federal Highway Administration (US Department of Transportation, Verenigde Staten) 2. Low Cost Measures (Elsamex Spanje) 3. Warnke Studie (Deutsche
ImFlow: BELEIDSMATIG VERKEERS MANAGEMENT
 ImFlow: BELEIDSMATIG VERKEERS MANAGEMENT Uw doelstellingen onder controle De slimme, duurzame stad Imflow zal de huidige manier van verkeersmanagement rigoureus veranderen. Effectief en duurzaam vervoer
ImFlow: BELEIDSMATIG VERKEERS MANAGEMENT Uw doelstellingen onder controle De slimme, duurzame stad Imflow zal de huidige manier van verkeersmanagement rigoureus veranderen. Effectief en duurzaam vervoer
Prestatieanalyse van de Turborotonde
 Prestatieanalyse van de Turborotonde Systematische benadering van de relatie tussen geometrisch ontwerp en capaciteit A.S. van Beinum Den Haag, april 27 Prestatieanalyse van de Turborotonde Systematische
Prestatieanalyse van de Turborotonde Systematische benadering van de relatie tussen geometrisch ontwerp en capaciteit A.S. van Beinum Den Haag, april 27 Prestatieanalyse van de Turborotonde Systematische
Hoe goed of slecht beleeft men de EOT-regeling? Hoe evolueert deze beleving in de eerste 30 maanden?
 Hoe goed of slecht beleeft men de EOT-regeling? Hoe evolueert deze beleving in de eerste 30 maanden? Auteur: Ruben Brondeel i.s.m. Prof. A. Buysse Onderzoeksvraag Tijdens het proces van een echtscheiding
Hoe goed of slecht beleeft men de EOT-regeling? Hoe evolueert deze beleving in de eerste 30 maanden? Auteur: Ruben Brondeel i.s.m. Prof. A. Buysse Onderzoeksvraag Tijdens het proces van een echtscheiding
Literatuurstudie naar de reële emissies van houtverbranding
 Vlaanderen is milieu Literatuurstudie naar de reële emissies van houtverbranding Eindrapport VLAAMSE MILIEUMAATSCHAPPIJ www.vmm.be V Management samenvatting Deze studie geeft een overzicht van de effectieve
Vlaanderen is milieu Literatuurstudie naar de reële emissies van houtverbranding Eindrapport VLAAMSE MILIEUMAATSCHAPPIJ www.vmm.be V Management samenvatting Deze studie geeft een overzicht van de effectieve
PROJECTNUMMER C ONZE REFERENTIE
 ONDERWERP Verkeersonderzoek Expo DATUM 1-2-2016 PROJECTNUMMER C05057.000035 ONZE REFERENTIE 078794434 0.8 VAN Anton van Meulen AAN Delta Development Group KOPIE AAN Nienke Spiegelenberg 1 Inleiding Hoeve
ONDERWERP Verkeersonderzoek Expo DATUM 1-2-2016 PROJECTNUMMER C05057.000035 ONZE REFERENTIE 078794434 0.8 VAN Anton van Meulen AAN Delta Development Group KOPIE AAN Nienke Spiegelenberg 1 Inleiding Hoeve
Snelweg invoegen en uitvoegen hoe?
 Snelweg invoegen en uitvoegen hoe? Snelweg vast procedure Ga je naar een ander stad waarbij je stukje op de snelweg moet rijden? Denk dan aan: Je route tot je eind bestemming. Welke ANWB borden je moet
Snelweg invoegen en uitvoegen hoe? Snelweg vast procedure Ga je naar een ander stad waarbij je stukje op de snelweg moet rijden? Denk dan aan: Je route tot je eind bestemming. Welke ANWB borden je moet
EINDNOTA UTOPIA Versie 1.1 /////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
 Expertise Verkeer en Telematica Graaf de Ferrarisgebouw Koning Albert II-laan 20 bus 4 1000 BRUSSEL T 02 533 78 01 expertise.verkeer.telematica@vlaanderen.be EINDNOTA UTOPIA Versie 1.1 /////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Expertise Verkeer en Telematica Graaf de Ferrarisgebouw Koning Albert II-laan 20 bus 4 1000 BRUSSEL T 02 533 78 01 expertise.verkeer.telematica@vlaanderen.be EINDNOTA UTOPIA Versie 1.1 /////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Capaciteitsanalyse Van Zijstweg
 Capaciteitsanalyse Van Zijstweg Resultaten simulatiestudie busbaan in zuidligging 2 x 1 2 x 1,5 BC 4490-101-100 21-10-13 1 Inhoudsopgave Doel Uitgangspunten Wijze van beoordeling verkeersafwikkeling Knoppen
Capaciteitsanalyse Van Zijstweg Resultaten simulatiestudie busbaan in zuidligging 2 x 1 2 x 1,5 BC 4490-101-100 21-10-13 1 Inhoudsopgave Doel Uitgangspunten Wijze van beoordeling verkeersafwikkeling Knoppen
1. De doorstroming op etmaalniveau op de t Goylaan is in 2017 t.o.v licht verbeterd;
 Arane Adviseurs in verkeer en vervoer Groen van Prinsterersingel 43b 2805 TD Gouda Memo e info@arane.nl t 0182 555 030 Van: Aan: Arane Adviseurs in verkeer en vervoer Gemeente Utrecht Datum: 6 april 2017
Arane Adviseurs in verkeer en vervoer Groen van Prinsterersingel 43b 2805 TD Gouda Memo e info@arane.nl t 0182 555 030 Van: Aan: Arane Adviseurs in verkeer en vervoer Gemeente Utrecht Datum: 6 april 2017
Het Effect van Verschil in Sociale Invloed van Ouders en Vrienden op het Alcoholgebruik van Adolescenten.
 Het Effect van Verschil in Sociale Invloed van Ouders en Vrienden op het Alcoholgebruik van Adolescenten. The Effect of Difference in Peer and Parent Social Influences on Adolescent Alcohol Use. Nadine
Het Effect van Verschil in Sociale Invloed van Ouders en Vrienden op het Alcoholgebruik van Adolescenten. The Effect of Difference in Peer and Parent Social Influences on Adolescent Alcohol Use. Nadine
360 FEEDBACK 10/08/2012. Thomas Commercieel Vragenlijst. Thomas Voorbeeld. Persoonlijk & Vertrouwelijk
 360 FEEDBACK 10/08/2012 Thomas Commercieel Vragenlijst Thomas Voorbeeld Persoonlijk & Vertrouwelijk S Hamilton-Gill & Thomas International Limited 1998-2013 http://www.thomasinternational.net 1 Inhoud
360 FEEDBACK 10/08/2012 Thomas Commercieel Vragenlijst Thomas Voorbeeld Persoonlijk & Vertrouwelijk S Hamilton-Gill & Thomas International Limited 1998-2013 http://www.thomasinternational.net 1 Inhoud
Vlaams actieplan voor veiligere verkeerslichten. Van Herzeele Stanny Agentschap Wegen en Verkeer
 Vlaams actieplan voor veiligere verkeerslichten Van Herzeele Stanny Agentschap Wegen en Verkeer Agenda Visie op slimmere verkeerslichten Voorgestelde optimalisaties actieplan Uitrol Resultaten Vragen Visie
Vlaams actieplan voor veiligere verkeerslichten Van Herzeele Stanny Agentschap Wegen en Verkeer Agenda Visie op slimmere verkeerslichten Voorgestelde optimalisaties actieplan Uitrol Resultaten Vragen Visie
Parkeerbehoefte berekenen, niet schatten
 (Bijdragenr. 71) Parkeerbehoefte berekenen, niet schatten Sjoerd Stienstra (ir. Sj. Stienstra Adviesbureau stedelijk verkeer BV) Samenvatting: Parkeerkentallen geven slechts een globale benadering van
(Bijdragenr. 71) Parkeerbehoefte berekenen, niet schatten Sjoerd Stienstra (ir. Sj. Stienstra Adviesbureau stedelijk verkeer BV) Samenvatting: Parkeerkentallen geven slechts een globale benadering van
Hoofdstuk 26: Modelleren in Excel
 Hoofdstuk 26: Modelleren in Excel 26.0 Inleiding In dit hoofdstuk leer je een aantal technieken die je kunnen helpen bij het voorbereiden van bedrijfsmodellen in Excel (zie hoofdstuk 25 voor wat bedoeld
Hoofdstuk 26: Modelleren in Excel 26.0 Inleiding In dit hoofdstuk leer je een aantal technieken die je kunnen helpen bij het voorbereiden van bedrijfsmodellen in Excel (zie hoofdstuk 25 voor wat bedoeld
EEN SIMULATIESTUDIE VAN DE SCHEDULE CONTROL INDEX
 EEN SIMULATIESTUDIE VAN DE SCHEDULE CONTROL INDEX Universiteit Gent Faculteit economie en bedrijfskunde Student X Tussentijds Rapport Promotor: prof. dr. M. Vanhoucke Begeleider: Y Academiejaar 20XX-20XX
EEN SIMULATIESTUDIE VAN DE SCHEDULE CONTROL INDEX Universiteit Gent Faculteit economie en bedrijfskunde Student X Tussentijds Rapport Promotor: prof. dr. M. Vanhoucke Begeleider: Y Academiejaar 20XX-20XX
Het verhaal van de financiële staart Jan Beirlant, Goedele Dierckx Universitair Centrum voor Statistiek en Departement Wiskunde, KULeuven
 Het verhaal van de financiële staart Jan Beirlant, Goedele Dierckx Universitair Centrum voor Statistiek en Departement Wiskunde, KULeuven In het secundair onderwijs wordt de 8-uur wiskunde nauwelijks nog
Het verhaal van de financiële staart Jan Beirlant, Goedele Dierckx Universitair Centrum voor Statistiek en Departement Wiskunde, KULeuven In het secundair onderwijs wordt de 8-uur wiskunde nauwelijks nog
360 FEEDBACK 30/07/2013. Thomas Vragenlijst
 360 FEEDBACK 30/07/2013 Thomas Vragenlijst Thomas Voorbeeld Persoonlijk & Vertrouwelijk S Hamilton-Gill & Thomas International Limited 1998-2013 http://www.thomasinternational.net 1 Inhoud Inhoud 2 Inleiding
360 FEEDBACK 30/07/2013 Thomas Vragenlijst Thomas Voorbeeld Persoonlijk & Vertrouwelijk S Hamilton-Gill & Thomas International Limited 1998-2013 http://www.thomasinternational.net 1 Inhoud Inhoud 2 Inleiding
Griepepidemie. Modelleren B. Javiér Sijen. Janine Sinke
 Javiér Sijen Janine Sinke Griepepidemie Modelleren B Om de uitbraak van een epidemie te voorspellen, wordt de verspreiding van een griepvirus gemodelleerd. Hierbij wordt zowel een detailbenadering als
Javiér Sijen Janine Sinke Griepepidemie Modelleren B Om de uitbraak van een epidemie te voorspellen, wordt de verspreiding van een griepvirus gemodelleerd. Hierbij wordt zowel een detailbenadering als
Modelleren C Appels. Christian Vleugels Sander Verkerk Richard Both. 2 april 2010. 1 Inleiding 2. 3 Data 3. 4 Aanpak 3
 Modelleren C Appels Christian Vleugels Sander Verkerk Richard Both 2 april 2010 Inhoudsopgave 1 Inleiding 2 2 Probleembeschrijving 2 3 Data 3 4 Aanpak 3 5 Data-analyse 4 5.1 Data-analyse: per product.............................
Modelleren C Appels Christian Vleugels Sander Verkerk Richard Both 2 april 2010 Inhoudsopgave 1 Inleiding 2 2 Probleembeschrijving 2 3 Data 3 4 Aanpak 3 5 Data-analyse 4 5.1 Data-analyse: per product.............................
Bestemmingsplan. Midden-Noord - Oss Ontwerp. Bijlagen 9 - aanvullend verkeersonderzoek maatregelen januari 2011 tuincentrum
 Bestemmingsplan Midden-Noord - Oss - 2012 Bijlagen 9 - aanvullend verkeersonderzoek maatregelen januari 2011 tuincentrum Ontwerp Deventer Den Haag Eindhoven Snipperlingsdijk 4 Verheeskade 197 Flight Forum
Bestemmingsplan Midden-Noord - Oss - 2012 Bijlagen 9 - aanvullend verkeersonderzoek maatregelen januari 2011 tuincentrum Ontwerp Deventer Den Haag Eindhoven Snipperlingsdijk 4 Verheeskade 197 Flight Forum
MFD op trajectniveau. Een empirische analyse. C.A. van Geffen R.P. van Denderen
 MFD op trajectniveau Een empirische analyse C.A. van Geffen R.P. van Denderen 29-6-2011 Inhoudsopgave 1 Inleiding... 2 1.1 Hoofdvraag... 2 1.2 Deelvragen... 2 2 Situatieschets... 3 2.1 Omgeving... 3 2.2
MFD op trajectniveau Een empirische analyse C.A. van Geffen R.P. van Denderen 29-6-2011 Inhoudsopgave 1 Inleiding... 2 1.1 Hoofdvraag... 2 1.2 Deelvragen... 2 2 Situatieschets... 3 2.1 Omgeving... 3 2.2
Memo. HaskoningDHV Nederland B.V. Transport & Planning
 Memo Aan: Dhr. W. Wullaert Van: Anneke Merkx Datum: 1 januari 201 Kopie: - Ons kenmerk: N002_T&P_BA5-102-101 Classificatie: Vertrouwelijk HaskoningDHV Nederland B.V. Transport & Planning Onderwerp: Verkeersgeneratie
Memo Aan: Dhr. W. Wullaert Van: Anneke Merkx Datum: 1 januari 201 Kopie: - Ons kenmerk: N002_T&P_BA5-102-101 Classificatie: Vertrouwelijk HaskoningDHV Nederland B.V. Transport & Planning Onderwerp: Verkeersgeneratie
