Moleculaire Dynamica en Monte Carlo Simulaties Case Study 17 Solid-Liquid Equilibrium of Hard Spheres. Joost van Bruggen juli 2004
|
|
|
- Theophiel Smet
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Moleculaire Dynamica en Monte Carlo Simulaties Case Study 17 Solid-Liquid Equilibrium of Hard Spheres Joost van Bruggen juli
2 Inhoudsopgave 1 Thermaliseren 2 2 Waarde van λ max 2 3 Integreren 2 4 het Berekenen 4 Samenvatting In dit verslag worden de resultaten van het werken aan Case Study 17 uit het boek van Frenkel en Smit [2] besproken. Er wordt tijdens de simulaties gebruik gemaakt van een fcc rooster met daarop verschillende aantallen deeltjes. De thermalisatietijd bedraagt 1000 Monte Carlo stappen. De waarde van λ max is 2000, c heeft de waarde 70 en de parameter ndispl heeft steeds de waarde Voor het berekenen van de integraal wordt gebruik gemaakt van een 10 punts Gaussische kwadratuur in combinatie met een coordinatentransformatie. Bovendien wordt een extrapolatie gemaakt naar oneindige systeem grootte, omdat de verkregen antwoorden van de grootte af blijken te hangen en we op zoek zijn naar een waarde voor macroscopische systemen. 1 Thermaliseren Om te kijken hoe lang de thermalisatietijden dienen te zijn, werd voor verschillende aantallen thermalisatiestappen gekeken hoe de uitkomst afhangt van die aantallen. Door steeds de thermalisatietijden te verhogen en te kijken naar de waarde van de gemiddelde kwadratische verplaatsing, werd gezocht naar een limiet waarde. Het verschil tussen de waarde van de gemiddelde kwadratische verplaatsing tussen opeenvolgende geprobeerde waarden voor de thermalisatietijd, werd steeds kleiner. Er is op deze manier gekozen voor een thermalisatietijd van 1000 Monte Carlo stappen. Dit lijkt een goede afweging tussen snelheid en nauwkeurigheid te zijn. 2 Waarde van λ max De waarde van λ max is op advies van het boek gekozen op In figuur 1 is te zien dat de met simulaties verkregen curve (zie notebooks op [1] voor details) zeker voor λ > λ max = 2000 voldoet aan de analytische oplossing van een Einstein solid. Hiermee kunnen we dus concluderen dat de gebruikte λ max goed gekozen is. 3 Integreren Om de resultaten uit de simulatie te verwerken, is, wederom op aanraden van Frenkel en Smit [2], gekozen voor een 10 punts Gaussische kwa- 2
3 0.014 r 2 rood : simulatie, groen : Einstein solid Λ Figuur 1: Vergelijking van de met simulaties verkregen curve met de voor het Einstein solid bekende analytische oplossing dratuur methode. Eveneens is de voorgestelde coordinatentransformatie toegepast. de coordinatentransformatie en Gaussische kwadratuur De voorgestelde coordinatentransformatie dient er voor om de functie gladder te laten verlopen zodat de kwadratuur methode een nauwkeuriger antwoord oplevert. Deze methode is namelijk geschikt om functies te integreren die benaderd kunnen worden door polynomen van graad tot 2 p met p het aantal evaluatiepunten in de Gaussische kwadratuur. Volgens de kwadratuur methode geldt: b a f(x)dx = N w i f(x i ), met N het aantal evaluatiepunten en f een willekeurige functie die, wil men een nauwkeurig antwoord krijgen, goed benaderd kan worden door een polynoom van graad maximaal 2N. i waarde van c In de coordinatentransformatie komt een parameter c voor die in de uitgevoerde experimenten steeds de waarde 70 had. 3
4 4 het Berekenen In deze sectie wordt stap voor stap het gevolgde traject tot het eindantwoord beschreven. Na het vaststellen van waarden voor alle parameters (zoals λ max en c), is er voor systemen van verschillende grootte gesimuleerd. Zie tabel 1 voor de gebruikte waarden. Dit simuleren is gedaan door de bij elke systeem grootte voor 10 verschillende waarden van λ te runnen. Die 10 waarden van λ zijn verkregen door gebruik te maken van Mathematica s GaussianQuadratureWeights, die ook meteen de gewichten w i uit de hierboven genoemde som oplevert. Zie voor de details weer de notebooks op [1]. Hierna is de som uitgerekend alsmede de fout (in het kwadraat) door kwadratische optelling van de uit de simulatie verkregen fouten. Als laatste zijn de door Frenkel en Smit [2] voorgestelde correcties toegepast. De verkregen resultaten zijn te vinden in tabel 1. systeem grootte (βf ex + Ln(N))/N fout 3*3*6 = *6*6 = *6*6 = *6*12 = *9*6 = Tabel 1: Resultaten van simulaties Omdat de te berekenen excess free energy enigszins afhangt van de grootte van het systeem, zoals blijkt uit de waarden in tabel 1, is een extrapolatie gemaakt naar oneindig grote systemen. De hiermee verkregen waarde voor de excess free energy bedraagt: 5.899(2). 4
5 Referenties [1] [2] Daan Frenkel en Berend Smit, Understanding Molecular Simulation, Academic Press (2002) 5
Tentamen Simulaties van biochemische systemen - 8C Juni uur
 Tentamen Simulaties van biochemische systemen - 8C110 8 Juni 010-900-100 uur Vier algemene opmerkingen: Het tentamen bestaat uit 7 opgaven verdeeld over 3 pagina s Op pagina 3 staat voor iedere opgave
Tentamen Simulaties van biochemische systemen - 8C110 8 Juni 010-900-100 uur Vier algemene opmerkingen: Het tentamen bestaat uit 7 opgaven verdeeld over 3 pagina s Op pagina 3 staat voor iedere opgave
Case Simulink EE4- Building a SSV - Team PM1 21 maart 2014
 Case Simulink EE4- Building a SSV - Team PM1 21 maart 2014 Inhoudsopgave Inhoudsopgave... 1 Figurenlijst... 1 Inleiding... 2 Gedrag van het zonnepaneel gekoppeld aan een weerstand... 2 Gedrag van de DC-motor
Case Simulink EE4- Building a SSV - Team PM1 21 maart 2014 Inhoudsopgave Inhoudsopgave... 1 Figurenlijst... 1 Inleiding... 2 Gedrag van het zonnepaneel gekoppeld aan een weerstand... 2 Gedrag van de DC-motor
Sterrenkunde Praktikum 1 Fouten en fitten
 Sterrenkunde Praktikum 1 Fouten en fitten Paul van der Werf 12 februari 2008 1 Inleiding In de sterrenkunde werken we vaak met zwakke signalen, of met grote hoeveelheden metingen van verschillende nauwkeurigheid.
Sterrenkunde Praktikum 1 Fouten en fitten Paul van der Werf 12 februari 2008 1 Inleiding In de sterrenkunde werken we vaak met zwakke signalen, of met grote hoeveelheden metingen van verschillende nauwkeurigheid.
5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2
![5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2 5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2](/thumbs/72/66414323.jpg) Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) = a b 5.1 Herleiden [1] Voorbeeld 1: (a + 5)(a 6) (a + 5)(-a + 7) = a 6a + 5a 30 ( a + 14a 5a + 35) = a 6a + 5a 30
Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) = a b 5.1 Herleiden [1] Voorbeeld 1: (a + 5)(a 6) (a + 5)(-a + 7) = a 6a + 5a 30 ( a + 14a 5a + 35) = a 6a + 5a 30
Monte-Carlo simulatie voor financiële optieprijzen Studiepunten : 2
 1 INLEIDING 1 Monte-Carlo simulatie voor financiële optieprijzen Studiepunten : 2 Volg stap voor stap de tekst en los de vragen op. Bedoeling is dat je op het einde van de rit een verzorgd verslag afgeeft
1 INLEIDING 1 Monte-Carlo simulatie voor financiële optieprijzen Studiepunten : 2 Volg stap voor stap de tekst en los de vragen op. Bedoeling is dat je op het einde van de rit een verzorgd verslag afgeeft
Tentamen Simulaties van biochemische systemen - 8C110 9 April uur
 Tentamen Simulaties van biochemische systemen - 8C0 9 April 200-900-200 uur Vier algemene opmerkingen: Het tentamen bestaat uit 6 opgaven verdeeld over pagina s Op pagina staat voor iedere opgave het maximale
Tentamen Simulaties van biochemische systemen - 8C0 9 April 200-900-200 uur Vier algemene opmerkingen: Het tentamen bestaat uit 6 opgaven verdeeld over pagina s Op pagina staat voor iedere opgave het maximale
Tentamen Simulaties van biochemische systemen - 8C110 3 juli uur
 Tentamen Simulaties van biochemische systemen - 8C0 3 juli 0-4.00-7.00 uur Vier algemene opmerkingen: Het tentamen bestaat uit 6 opgaven verdeeld over 3 pagina s. Op pagina 3 staat voor iedere opgave het
Tentamen Simulaties van biochemische systemen - 8C0 3 juli 0-4.00-7.00 uur Vier algemene opmerkingen: Het tentamen bestaat uit 6 opgaven verdeeld over 3 pagina s. Op pagina 3 staat voor iedere opgave het
1.1 Rekenen met letters [1]
![1.1 Rekenen met letters [1] 1.1 Rekenen met letters [1]](/thumbs/41/22623929.jpg) 1.1 Rekenen met letters [1] Voorbeeld 1: Een kaars heeft een lengte van 30 centimeter. Per uur brand er 6 centimeter van de kaars op. Hieruit volgt de volgende woordformule: Lengte in cm = -6 aantal branduren
1.1 Rekenen met letters [1] Voorbeeld 1: Een kaars heeft een lengte van 30 centimeter. Per uur brand er 6 centimeter van de kaars op. Hieruit volgt de volgende woordformule: Lengte in cm = -6 aantal branduren
Krachtenbalans op zandkorrels
 Krachtenbalans op zandkorrels Thijs J.H. Vlugt en Rianne van Eerd Debye Instituut afdeling Scheikunde Granulaire materialen zoals zand en graankorrels hebben eigenschappen overeenkomstig met zowel vloeistoffen
Krachtenbalans op zandkorrels Thijs J.H. Vlugt en Rianne van Eerd Debye Instituut afdeling Scheikunde Granulaire materialen zoals zand en graankorrels hebben eigenschappen overeenkomstig met zowel vloeistoffen
Bewegingen en Trillingen. Nokkenmechanisme: deel B
 Katholieke Universiteit Leuven Faculteit Ingenieurswetenschappen Departement Werktuigkunde Bewegingen en Trillingen Nokkenmechanisme: deel B Groepsnummer 35 Jan-Pieter Jacobs Christophe Mestdag 1 Inhoudsopgave
Katholieke Universiteit Leuven Faculteit Ingenieurswetenschappen Departement Werktuigkunde Bewegingen en Trillingen Nokkenmechanisme: deel B Groepsnummer 35 Jan-Pieter Jacobs Christophe Mestdag 1 Inhoudsopgave
Inhoud college 5 Basiswiskunde Taylorpolynomen
 Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Training integreren WISNET-HBO. update aug 2013
 Training integreren WISNET-HBO update aug 2013 Primitiveren De primitieve bepalen betekent in feite de functie bepalen waarvoor geldt dat Anders geschreven: Links en rechts maal dx: df = f dx De betekenis
Training integreren WISNET-HBO update aug 2013 Primitiveren De primitieve bepalen betekent in feite de functie bepalen waarvoor geldt dat Anders geschreven: Links en rechts maal dx: df = f dx De betekenis
college 6: limieten en l Hôpital
 126 college 6: ieten en l Hôpital In dit college herhalen we enkele belangrijke definities van ieten, en geven we belangrijke technieken om ieten van functies (eigenlijk en oneigenlijk) te bepalen. In
126 college 6: ieten en l Hôpital In dit college herhalen we enkele belangrijke definities van ieten, en geven we belangrijke technieken om ieten van functies (eigenlijk en oneigenlijk) te bepalen. In
Opgaven bij Numerieke Wiskunde I
 Opgaven bij Numerieke Wiskunde I 7 november 8 1. (a) Gegeven verschillende interpolatiepunten x, x 1, x [a, b], en getallen y, y 1, y, z 1, toon aan dat er hooguit 1 polynoom p P 3 is met p(x i ) = y i,
Opgaven bij Numerieke Wiskunde I 7 november 8 1. (a) Gegeven verschillende interpolatiepunten x, x 1, x [a, b], en getallen y, y 1, y, z 1, toon aan dat er hooguit 1 polynoom p P 3 is met p(x i ) = y i,
Monte-Carlo simulatie voor financiële optieprijzen Studiepunten : 3
 1 INLEIDING 1 Monte-Carlo simulatie voor financiële optieprijzen Studiepunten : 3 Volg stap voor stap de tekst en los de vragen op. Bedoeling is dat je op het einde van de rit een verzorgd verslag afgeeft
1 INLEIDING 1 Monte-Carlo simulatie voor financiële optieprijzen Studiepunten : 3 Volg stap voor stap de tekst en los de vragen op. Bedoeling is dat je op het einde van de rit een verzorgd verslag afgeeft
GridPix: Development and Characterisation of a Gaseous Tracking Detector W.J.C. Koppert
 GridPix: Development and Characterisation of a Gaseous Tracking Detector W.J.C. Koppert Samenvatting Deeltjes Detectie in Hoge Energie Fysica De positie waar de botsing heeft plaatsgevonden in een versneller
GridPix: Development and Characterisation of a Gaseous Tracking Detector W.J.C. Koppert Samenvatting Deeltjes Detectie in Hoge Energie Fysica De positie waar de botsing heeft plaatsgevonden in een versneller
University of Groningen. Interfacial action of phospholipase A2 Meulenhoff, Peter
 University of Groningen Interfacial action of phospholipase A2 Meulenhoff, Peter IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please
University of Groningen Interfacial action of phospholipase A2 Meulenhoff, Peter IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please
Riemannsommen en integralen
 Riemannsommen en integralen MET DE TI-NSPIRE Vervangt een deel van 0. uit VWO B deel gghm EEBII 0-0 Inhoud Oppervlakte onder de grafiek... Ondersom... 4 Bovensom... 4 Middensom... 4 Riemannsom... 5 Riemannsom
Riemannsommen en integralen MET DE TI-NSPIRE Vervangt een deel van 0. uit VWO B deel gghm EEBII 0-0 Inhoud Oppervlakte onder de grafiek... Ondersom... 4 Bovensom... 4 Middensom... 4 Riemannsom... 5 Riemannsom
Rapport Triple A - Risk Finance B.V. terzake Vergelijking pensioenproduct met de markt voor
 Rapport Triple A - Risk Finance B.V. terzake Vergelijking pensioenproduct met de markt voor Zwitserleven N.V. Inhoudsopgave 1. Management samenvatting...1 2. Zwitserleven DC Product...2 3. Beschrijving
Rapport Triple A - Risk Finance B.V. terzake Vergelijking pensioenproduct met de markt voor Zwitserleven N.V. Inhoudsopgave 1. Management samenvatting...1 2. Zwitserleven DC Product...2 3. Beschrijving
Tentamen Moleculaire Simulaties - 8C November uur
 Tentamen Moleculaire Simulaties - 8C030 11 November 2008-14.00-17.00 uur Vier algemene opmerkingen: Het tentamen bestaat uit 6 opgaven verdeeld over 3 pagina's. Op pagina 3 staat voor iedere opgave het
Tentamen Moleculaire Simulaties - 8C030 11 November 2008-14.00-17.00 uur Vier algemene opmerkingen: Het tentamen bestaat uit 6 opgaven verdeeld over 3 pagina's. Op pagina 3 staat voor iedere opgave het
Bepaling energie en soortelijke warmte 2D-atoomrooster m.b.v. de Metropolis Monte Carlo methode
 Bepaling energie en soortelijke warmte 2D-atoomrooster m.b.v. de Metropolis Monte Carlo methode Verslag Computational Physics Sietze van Buuren Begeleider: Prof.Dr. H. de Raedt 29 december 25 Samenvatting
Bepaling energie en soortelijke warmte 2D-atoomrooster m.b.v. de Metropolis Monte Carlo methode Verslag Computational Physics Sietze van Buuren Begeleider: Prof.Dr. H. de Raedt 29 december 25 Samenvatting
Griepepidemie. Modelleren B. Javiér Sijen. Janine Sinke
 Javiér Sijen Janine Sinke Griepepidemie Modelleren B Om de uitbraak van een epidemie te voorspellen, wordt de verspreiding van een griepvirus gemodelleerd. Hierbij wordt zowel een detailbenadering als
Javiér Sijen Janine Sinke Griepepidemie Modelleren B Om de uitbraak van een epidemie te voorspellen, wordt de verspreiding van een griepvirus gemodelleerd. Hierbij wordt zowel een detailbenadering als
Eindexamen wiskunde A1 compex vwo 2007-I
 Gemeenteraadsverkiezingen Op 2 maart 1994 vonden er in Nederland gemeenteraadsverkiezingen plaats. In de gemeente Enschede werden 67 787 stemmen uitgebracht. Open GEMEENTERAADSVERKIEZINGEN.XLS Vraag 14,15.
Gemeenteraadsverkiezingen Op 2 maart 1994 vonden er in Nederland gemeenteraadsverkiezingen plaats. In de gemeente Enschede werden 67 787 stemmen uitgebracht. Open GEMEENTERAADSVERKIEZINGEN.XLS Vraag 14,15.
Verwachtingswaarde, Variantie en Standaarddeviatie
 Verwachtingswaarde, Variantie en Standaarddeviatie Wisnet-hbo Verwachtingswaarde update maart 200 De verwachtingswaarde van een kansvariabele is een soort gemiddelde waarde. Deze wordt aangeduid met E(k)
Verwachtingswaarde, Variantie en Standaarddeviatie Wisnet-hbo Verwachtingswaarde update maart 200 De verwachtingswaarde van een kansvariabele is een soort gemiddelde waarde. Deze wordt aangeduid met E(k)
HOOFDSTUK I - INLEIDENDE BEGRIPPEN
 HOOFDSTUK I - INLEIDENDE BEGRIPPEN 1.2 Kansveranderlijken en verdelingen 1 Veranderlijken Beschouw een toevallig experiment met uitkomstenverzameling V (eindig of oneindig), de verzameling van alle gebeurtenissen
HOOFDSTUK I - INLEIDENDE BEGRIPPEN 1.2 Kansveranderlijken en verdelingen 1 Veranderlijken Beschouw een toevallig experiment met uitkomstenverzameling V (eindig of oneindig), de verzameling van alle gebeurtenissen
wiskunde B havo 2018-II
 Piano In figuur 1 zijn de witte en zwarte toetsen van een gewone piano getekend. In totaal heeft deze piano 88 toetsen. figuur 1 De toetsen worden genummerd van links naar rechts. Zie figuur, waarin de
Piano In figuur 1 zijn de witte en zwarte toetsen van een gewone piano getekend. In totaal heeft deze piano 88 toetsen. figuur 1 De toetsen worden genummerd van links naar rechts. Zie figuur, waarin de
TECHNISCHE UNIVERSITEIT EINDHOVEN. Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10)
 TECHNISCHE UNIVERSITEIT EINDHOVEN Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10) en Tentamen Inleiding Experimentele Fysica voor Combi s (3NA10) d.d. 31 oktober 2011 van 9:00 12:00 uur Vul de
TECHNISCHE UNIVERSITEIT EINDHOVEN Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10) en Tentamen Inleiding Experimentele Fysica voor Combi s (3NA10) d.d. 31 oktober 2011 van 9:00 12:00 uur Vul de
(x x 1 ) + y 1. x x 1 x k x x x k 1
 Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Les Taylor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Praktische opdracht Wiskunde som van de ogen van drie dobbelstenen
 Praktische opdracht Wiskunde som van de ogen van drie dobbelstenen Praktische-opdracht door een scholier 918 woorden 17 maart 2002 4,9 60 keer beoordeeld Vak Wiskunde Inleiding Wij hebben gekozen voor
Praktische opdracht Wiskunde som van de ogen van drie dobbelstenen Praktische-opdracht door een scholier 918 woorden 17 maart 2002 4,9 60 keer beoordeeld Vak Wiskunde Inleiding Wij hebben gekozen voor
1. Statistiek gebruiken 1
 Hoofdstuk 0 Inhoudsopgave 1. Statistiek gebruiken 1 2. Gegevens beschrijven 3 2.1 Verschillende soorten gegevens......................................... 3 2.2 Staafdiagrammen en histogrammen....................................
Hoofdstuk 0 Inhoudsopgave 1. Statistiek gebruiken 1 2. Gegevens beschrijven 3 2.1 Verschillende soorten gegevens......................................... 3 2.2 Staafdiagrammen en histogrammen....................................
Principe Maken van een Monte Carlo data-set populatie-parameters en standaarddeviaties standaarddeviatie van de bepaling statistische verdeling
 Monte Carlo simulatie In MW\Pharm versie 3.30 is een Monte Carlo simulatie-module toegevoegd. Met behulp van deze Monte Carlo procedure kan onder meer de betrouwbaarheid van de berekeningen van KinPop
Monte Carlo simulatie In MW\Pharm versie 3.30 is een Monte Carlo simulatie-module toegevoegd. Met behulp van deze Monte Carlo procedure kan onder meer de betrouwbaarheid van de berekeningen van KinPop
Dusty Plasma : Vorming van C-nanoclusters
 Dusty Plasma : Vorming van C-nanoclusters Sammy De Souter Abstract Een MD simulatie werd uitgevoerd om te onderzoeken hoe nanoclusters gevormd worden in een acetyleen plasma en hoe dit varieert in functie
Dusty Plasma : Vorming van C-nanoclusters Sammy De Souter Abstract Een MD simulatie werd uitgevoerd om te onderzoeken hoe nanoclusters gevormd worden in een acetyleen plasma en hoe dit varieert in functie
(x x 1 ) + y 1. x x k+1 x k x k+1
 Les Talor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
Les Talor reeksen We hebben in Wiskunde een aantal belangrijke reële functies gezien, bijvoorbeeld de exponentiële functie exp(x) of de trigonometrische functies sin(x) en cos(x) Toen hebben we wel eigenschappen
OPPERVLAKTEBEREKENING MET DE TI83
 WERKBLAD OPPERVLAKTEBEREKENING MET DE TI83 Gevraagd de oppervlakte van het vlakdeel begrensd door de X as 3 grafiek f : x x 4x + x + x = en x = Oplossing Vermits we hier te doen hebben met een willekeurige
WERKBLAD OPPERVLAKTEBEREKENING MET DE TI83 Gevraagd de oppervlakte van het vlakdeel begrensd door de X as 3 grafiek f : x x 4x + x + x = en x = Oplossing Vermits we hier te doen hebben met een willekeurige
De verstrooide professor
 Inleiding De verstrooide professor Edward Omey HU - Stormstraat 2 000 russel edward.omey@hubrussel.be In hun nota bestuderen Guido Herweyers en Ronald Rouseau (G. Herweyers en R. Rousseau, Een onverwacht
Inleiding De verstrooide professor Edward Omey HU - Stormstraat 2 000 russel edward.omey@hubrussel.be In hun nota bestuderen Guido Herweyers en Ronald Rouseau (G. Herweyers en R. Rousseau, Een onverwacht
Experiment DutchBE (Belgium) Dansende korrels - Een model voor fase-overgangen en instabiliteiten
 Q2-1 Dansende korrels - Een model voor fase-overgangen en instabiliteiten (10 punten) Lees de algemene instructies in de aparte enveloppe voor je met het experiment begint. Introductie Fase-overgangen
Q2-1 Dansende korrels - Een model voor fase-overgangen en instabiliteiten (10 punten) Lees de algemene instructies in de aparte enveloppe voor je met het experiment begint. Introductie Fase-overgangen
De parabool en de cirkel raken elkaar in de oorsprong; bepaal ook de coördinaten van de overige snijpunten A 1 en A 2.
 BURGERLIJK INGENIEUR-ARCHITECT - 5 SEPTEMBER 2002 BLZ 1/10 1. We beschouwen de cirkel met vergelijking x 2 + y 2 2ry = 0 en de parabool met vergelijking y = ax 2. Hierbij zijn r en a parameters waarvoor
BURGERLIJK INGENIEUR-ARCHITECT - 5 SEPTEMBER 2002 BLZ 1/10 1. We beschouwen de cirkel met vergelijking x 2 + y 2 2ry = 0 en de parabool met vergelijking y = ax 2. Hierbij zijn r en a parameters waarvoor
Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde
 Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde voor B. 1 Eenvoudige operaties en functies. 1. De bewerkingen optellen aftrekken, vermenigvuldigen, delen en machtsverheffen worden
Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde voor B. 1 Eenvoudige operaties en functies. 1. De bewerkingen optellen aftrekken, vermenigvuldigen, delen en machtsverheffen worden
2 Vraagstuk Dynamicaboek (Kermisattractie)
 Kermisattractie Wisnet-HB update april 009 1 Benodigde wiskunde-onderwerpen Vectoren (eerst in de R) Poolcoördinaten (r en φ) Differentiëren (plaats, snelheid en versnelling en maximum/minimum bepalen)
Kermisattractie Wisnet-HB update april 009 1 Benodigde wiskunde-onderwerpen Vectoren (eerst in de R) Poolcoördinaten (r en φ) Differentiëren (plaats, snelheid en versnelling en maximum/minimum bepalen)
Eindexamen wiskunde A1-2 vwo 2005-I
 Eindexamen wiskunde A- vwo 005-I 4 Beoordelingsmodel Meer neerslag de opmerking dat de gemiddelde jaarlijkse neerslag in beide plaatsen gelijk is De standaardafwijking in Winterswijk is groter (en dus
Eindexamen wiskunde A- vwo 005-I 4 Beoordelingsmodel Meer neerslag de opmerking dat de gemiddelde jaarlijkse neerslag in beide plaatsen gelijk is De standaardafwijking in Winterswijk is groter (en dus
Dynamica van de logistische afbeelding. chaos 08-09
 Dynamica van de logistische afbeelding. chaos 08-09 Daniël Wedema January 12, 2009 1 inleiding In 1976 publiceerde May een artikel waarin hij liet zien dat hele simpele nietlineaire dynamische systemen
Dynamica van de logistische afbeelding. chaos 08-09 Daniël Wedema January 12, 2009 1 inleiding In 1976 publiceerde May een artikel waarin hij liet zien dat hele simpele nietlineaire dynamische systemen
Examen HAVO. wiskunde B. tijdvak 2 woensdag 20 juni uur. Bij dit examen hoort een uitwerkbijlage.
 Eamen HAV 018 tijdvak woensdag 0 juni 1.0-16.0 uur wiskunde B Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 18 vragen. Voor dit eamen zijn maimaal 7 punten te behalen. Voor elk vraagnummer
Eamen HAV 018 tijdvak woensdag 0 juni 1.0-16.0 uur wiskunde B Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 18 vragen. Voor dit eamen zijn maimaal 7 punten te behalen. Voor elk vraagnummer
Statistiek in een rechtzaak
 Statistiek in een rechtzaak Maarten van Kampen & Soon-Yip Wong 1 april 00 1 Schuldig of niet? Naar aanleiding van een recent krantenartikel over de rechtzaak omtrent Lucy B. willen wij onderzoeken wat
Statistiek in een rechtzaak Maarten van Kampen & Soon-Yip Wong 1 april 00 1 Schuldig of niet? Naar aanleiding van een recent krantenartikel over de rechtzaak omtrent Lucy B. willen wij onderzoeken wat
Examen VWO. wiskunde A1 Compex. Vragen 14 tot en met 19. In dit deel van het examen staan de vragen waarbij de computer wel wordt gebruikt.
 Examen VWO 2007 tijdvak 1 vrijdag 1 juni totale examentijd 3,5 uur wiskunde A1 Compex Vragen 14 tot en met 19 In dit deel van het examen staan de vragen waarbij de computer wel wordt gebruikt. Het gehele
Examen VWO 2007 tijdvak 1 vrijdag 1 juni totale examentijd 3,5 uur wiskunde A1 Compex Vragen 14 tot en met 19 In dit deel van het examen staan de vragen waarbij de computer wel wordt gebruikt. Het gehele
Samenvatting. (summary in Dutch)
 Samenvatting (summary in Dutch) Alle stoffen die we in de wereld om ons heen zien, zijn opgebouwd uit atomen, die onderling aan elkaar binden. Elk type atoom heeft de eigenschap dat het een sterke voorkeur
Samenvatting (summary in Dutch) Alle stoffen die we in de wereld om ons heen zien, zijn opgebouwd uit atomen, die onderling aan elkaar binden. Elk type atoom heeft de eigenschap dat het een sterke voorkeur
Overzicht Fourier-theorie
 B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
Primitiveren. Omgekeerd differentiëren (primitieve bepalen)
 Primitiveren WISNET-HBO update april 2006 Inleiding Soms moet je juist de functie bepalen waarvan de afgeleide bekend is. Dit omgekeerd differentiëren (de primitieve bepalen) heet in het Engels de antiderivative.
Primitiveren WISNET-HBO update april 2006 Inleiding Soms moet je juist de functie bepalen waarvan de afgeleide bekend is. Dit omgekeerd differentiëren (de primitieve bepalen) heet in het Engels de antiderivative.
Uit te voeren in groepen van 2 personen. Indien een groep van 2 personen niet mogelijk is, dient de opdracht alleen uitgevoerd te worden
 Solidworks Simulation: Opdracht versie 2014 Uit te voeren in groepen van 2 personen. Indien een groep van 2 personen niet mogelijk is, dient de opdracht alleen uitgevoerd te worden De opdracht Een fietsen
Solidworks Simulation: Opdracht versie 2014 Uit te voeren in groepen van 2 personen. Indien een groep van 2 personen niet mogelijk is, dient de opdracht alleen uitgevoerd te worden De opdracht Een fietsen
Schooljaar: Leerkracht: M. Smet Leervak: Wiskunde Leerplan: D/2002/0279/048
 Blz: 1/5 04 09 09 1.1 STELLING VAN PYTHAGORAS ouwregel tot Pythagoras: formulering. 07 09 09 11 09 09 14 09 09 18 09 09 21 09 09 22 09 09 25 09 09 29 09 09 01 10 09 02 10 09 06 10 09 08 10 09 09 10 09
Blz: 1/5 04 09 09 1.1 STELLING VAN PYTHAGORAS ouwregel tot Pythagoras: formulering. 07 09 09 11 09 09 14 09 09 18 09 09 21 09 09 22 09 09 25 09 09 29 09 09 01 10 09 02 10 09 06 10 09 08 10 09 09 10 09
Wetenschappelijk Rekenen
 Wetenschappelijk Rekenen Examen - Bacheloropleiding informatica Oefeningen 3 september 204. Beschouw de matrix A = 8 6 3 5 7 4 9 2 Deze matrix heeft 5 als dominante eigenwaarde. We proberen deze eigenwaarde
Wetenschappelijk Rekenen Examen - Bacheloropleiding informatica Oefeningen 3 september 204. Beschouw de matrix A = 8 6 3 5 7 4 9 2 Deze matrix heeft 5 als dominante eigenwaarde. We proberen deze eigenwaarde
BEREKENING SCHEURKANSEN VOOR VERHARDENDE BETONNEN ELEMENTEN
 BEREKENING SCHEURKANSEN VOOR VERHARDENDE BETONNEN ELEMENTEN MSc. H.W.M. van der Ham Dr. E.A.B. Koenders Prof. Dr. K. van Breugel DIANA Ontwikkelings Verening Technische lezingen 31 oktober 26 Presenting
BEREKENING SCHEURKANSEN VOOR VERHARDENDE BETONNEN ELEMENTEN MSc. H.W.M. van der Ham Dr. E.A.B. Koenders Prof. Dr. K. van Breugel DIANA Ontwikkelings Verening Technische lezingen 31 oktober 26 Presenting
Hoofdstuk 5. Dobbelen, echt en virtueel. > Maak in SPSS een nieuwe data-verzameling (File > New > Data). We gaan hier de
 Hoofdstuk 5 Dobbelen, echt en virtueel 5.1 dobbelen In dit hoofdstukje gaan we de variabiliteit in een steekproef onderzoeken. Daarbij maken we gebruik van een beproefd stochastisch proces, nl het gooien
Hoofdstuk 5 Dobbelen, echt en virtueel 5.1 dobbelen In dit hoofdstukje gaan we de variabiliteit in een steekproef onderzoeken. Daarbij maken we gebruik van een beproefd stochastisch proces, nl het gooien
De bisectie methode uitgelegd met een makkelijk voorbeeld
 De Bisectie methode De bisectie methode uitgelegd met een makkelijk voorbeeld De bisectie methode is een recursieve methode om punten van een functie te gaan afschatten. Hierbij gaat men de functiewaarde
De Bisectie methode De bisectie methode uitgelegd met een makkelijk voorbeeld De bisectie methode is een recursieve methode om punten van een functie te gaan afschatten. Hierbij gaat men de functiewaarde
1 Delers 1. 3 Grootste gemene deler en kleinste gemene veelvoud 12
 Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
integreren is het omgekeerde van differentiëren
 Integraalrekening Als we een functie f(x) differentiëren is het resultaat de eerste afgeleide f (x). Dezelfde functie f(x) kunnen we ook integreren met als resultaat de zogenaamde primitieve functie F(x).
Integraalrekening Als we een functie f(x) differentiëren is het resultaat de eerste afgeleide f (x). Dezelfde functie f(x) kunnen we ook integreren met als resultaat de zogenaamde primitieve functie F(x).
Het uitwendig product van twee vectoren
 Het uitwendig product van twee vectoren Als u, v R 3, u = u 1, u 2, u 3 en v = v 1, v 2, v 3 dan is het uitwendig product van u en v gelijk aan een vector in R 3 en wel u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3,
Het uitwendig product van twee vectoren Als u, v R 3, u = u 1, u 2, u 3 en v = v 1, v 2, v 3 dan is het uitwendig product van u en v gelijk aan een vector in R 3 en wel u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3,
R.B. Kappetein. Callcenters. Bachelorscriptie, 5 juli 2011. Scriptiebegeleider: Dr. F.M. Spieksma. Mathematisch Instituut, Universiteit Leiden
 R.B. Kappetein Callcenters Bachelorscriptie, 5 juli 2011 Scriptiebegeleider: Dr. F.M. Spieksma Mathematisch Instituut, Universiteit Leiden Inhoudsopgave 1 Inleiding: callcenters met ongeduldige klanten
R.B. Kappetein Callcenters Bachelorscriptie, 5 juli 2011 Scriptiebegeleider: Dr. F.M. Spieksma Mathematisch Instituut, Universiteit Leiden Inhoudsopgave 1 Inleiding: callcenters met ongeduldige klanten
Het drie-reservoirs probleem
 Modelleren A WH01 Het drie-reservoirs probleem Michiel Schipperen (0751733) Stephan van den Berkmortel (077098) Begeleider: Arris Tijsseling juni 01 Inhoudsopgave 1 Samenvatting Inleiding.1 De probleemstelling.................................
Modelleren A WH01 Het drie-reservoirs probleem Michiel Schipperen (0751733) Stephan van den Berkmortel (077098) Begeleider: Arris Tijsseling juni 01 Inhoudsopgave 1 Samenvatting Inleiding.1 De probleemstelling.................................
1.0 Voorkennis. Voorbeeld 1: Los op: 6x + 28 = 30 10x.
 1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
7. Hamiltoniaanse systemen
 7. Hamiltoniaanse systemen In de moleculaire dynamica, maar ook in andere gebieden zoals de hemelmechanica of klassieke mechanica, worden oplossingen gezocht van het Hamiltoniaanse systeem van differentiaalvergelijkingen
7. Hamiltoniaanse systemen In de moleculaire dynamica, maar ook in andere gebieden zoals de hemelmechanica of klassieke mechanica, worden oplossingen gezocht van het Hamiltoniaanse systeem van differentiaalvergelijkingen
Modelleren C Appels. Christian Vleugels Sander Verkerk Richard Both. 15 juni 2010. 1 Inleiding 2. 3 Data 3. 4 Aanpak 4
 Modelleren C Appels Christian Vleugels Sander Verkerk Richard Both 15 juni 2010 Inhoudsopgave 1 Inleiding 2 2 Probleembeschrijving 2 3 Data 3 4 Aanpak 4 5 Deterministische aanpak 4 5.1 Populariteit van
Modelleren C Appels Christian Vleugels Sander Verkerk Richard Both 15 juni 2010 Inhoudsopgave 1 Inleiding 2 2 Probleembeschrijving 2 3 Data 3 4 Aanpak 4 5 Deterministische aanpak 4 5.1 Populariteit van
werkcollege 5 - P&D7: Population distributions - P&D8: Sampling variability and Sampling distributions
 cursus 4 mei 2012 werkcollege 5 - P&D7: Population distributions - P&D8: Sampling variability and Sampling distributions Huiswerk P&D, opgaven Chapter 6: 9, 19, 25, 33 P&D, opgaven Appendix A: 1, 9 doen
cursus 4 mei 2012 werkcollege 5 - P&D7: Population distributions - P&D8: Sampling variability and Sampling distributions Huiswerk P&D, opgaven Chapter 6: 9, 19, 25, 33 P&D, opgaven Appendix A: 1, 9 doen
Examen Complexe Analyse vrijdag 20 juni 2014, 14:00 18:00 uur Auditorium De Molen. Het examen bestaat uit 4 schriftelijke vragen.
 Examen Complexe Analyse vrijdag 0 juni 04, 4:00 8:00 uur Auditorium De Molen Naam: Studierichting: Het examen bestaat uit 4 schriftelijke vragen. Elke vraag telt even zwaar mee. Het boek Visual Complex
Examen Complexe Analyse vrijdag 0 juni 04, 4:00 8:00 uur Auditorium De Molen Naam: Studierichting: Het examen bestaat uit 4 schriftelijke vragen. Elke vraag telt even zwaar mee. Het boek Visual Complex
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D. Datum: Donderdag 8 juli 4. Tijd: 14. 17. uur. Plaats: MA 1.44/1.46 Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D. Datum: Donderdag 8 juli 4. Tijd: 14. 17. uur. Plaats: MA 1.44/1.46 Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je
Meten en experimenteren
 Meten en experimenteren Statistische verwerking van gegevens Een korte inleiding 5 oktober 007 Catherine De Clercq Statistische verwerking van gegevens Kursus statistiek voor fysici door Jorgen D Hondt
Meten en experimenteren Statistische verwerking van gegevens Een korte inleiding 5 oktober 007 Catherine De Clercq Statistische verwerking van gegevens Kursus statistiek voor fysici door Jorgen D Hondt
math inside Model orde reductie
 math inside Model orde reductie Model orde reductie Met het voortschrijden van de rekenkracht van computers en numerieke algoritmen is het mogelijk om steeds complexere problemen op te lossen. Was het
math inside Model orde reductie Model orde reductie Met het voortschrijden van de rekenkracht van computers en numerieke algoritmen is het mogelijk om steeds complexere problemen op te lossen. Was het
- Is het experiment bedoeld aas toetsing van een theorie? Is in het kort de theoretische achtergrond aan te geven?
 T.H.E. Vm-64/20. Opbouw en indeling van een rapport betreffende een emeriment. Gegeven wordt de globale indeling van een verslag zoals die door ondergetekende als meest logische wordt gezien. Bij ieder
T.H.E. Vm-64/20. Opbouw en indeling van een rapport betreffende een emeriment. Gegeven wordt de globale indeling van een verslag zoals die door ondergetekende als meest logische wordt gezien. Bij ieder
8. Differentiaal- en integraalrekening
 Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Statistiek voor Natuurkunde Opgavenserie 1: Kansrekening
 Statistiek voor Natuurkunde Opgavenserie 1: Kansrekening Inleveren: 12 januari 2011, VOOR het college Afspraken Serie 1 mag gemaakt en ingeleverd worden in tweetallen. Schrijf duidelijk je naam, e-mail
Statistiek voor Natuurkunde Opgavenserie 1: Kansrekening Inleveren: 12 januari 2011, VOOR het college Afspraken Serie 1 mag gemaakt en ingeleverd worden in tweetallen. Schrijf duidelijk je naam, e-mail
Opgave 3 - Uitwerking
 Mathrace 2014 Opgave 3 - Uitwerking Teken de rode hulplijntjes, en noem de lengte van dit lijntje y. Noem verder de lengte van een zijde van de gelijkzijdige driehoek x. Door de hoek van 45 graden in de
Mathrace 2014 Opgave 3 - Uitwerking Teken de rode hulplijntjes, en noem de lengte van dit lijntje y. Noem verder de lengte van een zijde van de gelijkzijdige driehoek x. Door de hoek van 45 graden in de
vandaag is Annie twee jaar jonger dan Ben en Cees samen
 Hoofdstuk I Lineaire Algebra Les 1 Stelsels lineaire vergelijkingen Om te beginnen is hier een puzzeltje: vandaag is Annie twee jaar jonger dan Ben en Cees samen over vijf jaar is Annie twee keer zo oud
Hoofdstuk I Lineaire Algebra Les 1 Stelsels lineaire vergelijkingen Om te beginnen is hier een puzzeltje: vandaag is Annie twee jaar jonger dan Ben en Cees samen over vijf jaar is Annie twee keer zo oud
Beoordelingsmodel. Antwoorden VWO wa I. Deelscores. Meer neerslag
 Beoordelingsmodel Antwoorden VWO wa 005-I Meer neerslag Maximumscore de opmerking dat de gemiddelde jaarlijkse neerslag in beide plaatsen gelijk is De standaardafwijking in Winterswijk is groter (en dus
Beoordelingsmodel Antwoorden VWO wa 005-I Meer neerslag Maximumscore de opmerking dat de gemiddelde jaarlijkse neerslag in beide plaatsen gelijk is De standaardafwijking in Winterswijk is groter (en dus
Populair-wetenschappelijke samenvatting
 Populair-wetenschappelijke samenvatting Dit proefschrift gaat over zwaartekracht, en een aantal van de bijzondere effecten die zij heeft op de beweging van sterren wanneer die extreem dicht bij elkaar
Populair-wetenschappelijke samenvatting Dit proefschrift gaat over zwaartekracht, en een aantal van de bijzondere effecten die zij heeft op de beweging van sterren wanneer die extreem dicht bij elkaar
Werkblad 2 Kracht is een vector -Thema 14 (NIVEAU BETA)
 Werkblad 2 Kracht is een vector -Thema 14 (NIVEAU BETA) Practicum Bij een gedeelte van het practicum zijn minimaal 3 deelnemers nodig. Leerlingen die op niveau gevorderd, of basis werken kunnen je helpen
Werkblad 2 Kracht is een vector -Thema 14 (NIVEAU BETA) Practicum Bij een gedeelte van het practicum zijn minimaal 3 deelnemers nodig. Leerlingen die op niveau gevorderd, of basis werken kunnen je helpen
Hoofdstuk 2 - Kwadratische functies
 Hoofdstuk - Kwadratische functies Hoofdstuk - Kwadratische functies Voorkennis V-1a y = 3(x ) 3 x 3 6x 1 y = 6x 1 b y = 9( 4x 4) 3 4x 4 9 36x 36 y = 36x 36 c y = x( x 7) 3 x 7 x x 7x y = x 7x V-a y = (
Hoofdstuk - Kwadratische functies Hoofdstuk - Kwadratische functies Voorkennis V-1a y = 3(x ) 3 x 3 6x 1 y = 6x 1 b y = 9( 4x 4) 3 4x 4 9 36x 36 y = 36x 36 c y = x( x 7) 3 x 7 x x 7x y = x 7x V-a y = (
Monte-Carlo simulatie voor financiële optieprijzen
 1 INLEIDING 1 Monte-Carlo simulatie voor financiële optieprijzen Docent: Karel in t Hout Studiepunten: 3 Volg stap voor stap de tekst en los de vragen op. Bedoeling is dat je op het einde van de rit een
1 INLEIDING 1 Monte-Carlo simulatie voor financiële optieprijzen Docent: Karel in t Hout Studiepunten: 3 Volg stap voor stap de tekst en los de vragen op. Bedoeling is dat je op het einde van de rit een
Weerwolven van Wakkerdam
 Weerwolven van Wakkerdam Jorritsma Joost 0748615 Swevels Barry 0716899 24 oktober 2011 1 Inhoudsopgave 1 Inleiding 3 2 Opdracht 4 3 Rollen 5 3.1 Gewone burgers................................. 5 3.2 Weerwolven...................................
Weerwolven van Wakkerdam Jorritsma Joost 0748615 Swevels Barry 0716899 24 oktober 2011 1 Inhoudsopgave 1 Inleiding 3 2 Opdracht 4 3 Rollen 5 3.1 Gewone burgers................................. 5 3.2 Weerwolven...................................
Validatie van simulatiemethode in Open FOAM
 Validatie van simulatiemethode in Open FOAM Samenvatting Dit verslag gaat over of een simulatie uitgevoerd in Open FOAM voldoende nauwkeurigheid bied en tevens uitvoerbaar is op een gewone computer. Er
Validatie van simulatiemethode in Open FOAM Samenvatting Dit verslag gaat over of een simulatie uitgevoerd in Open FOAM voldoende nauwkeurigheid bied en tevens uitvoerbaar is op een gewone computer. Er
Tentamenset A. 2. Welke van de volgende beweringen is waar? c. N R N d. R Z R
 Tentamenset A. Gegeven de volgende verzamelingen A en B. A is de verzameling van alle gehele getallen tussen de 0 en 0 die deelbaar zijn door, en B is de verzameling gehele positieve getallen deelbaar
Tentamenset A. Gegeven de volgende verzamelingen A en B. A is de verzameling van alle gehele getallen tussen de 0 en 0 die deelbaar zijn door, en B is de verzameling gehele positieve getallen deelbaar
Uitwerkingen toets 12 juni 2010
 Uitwerkingen toets 12 juni 2010 Opgave 1. Bekijk rijen a 1, a 2, a 3,... van positieve gehele getallen. Bepaal de kleinst mogelijke waarde van a 2010 als gegeven is: (i) a n < a n+1 voor alle n 1, (ii)
Uitwerkingen toets 12 juni 2010 Opgave 1. Bekijk rijen a 1, a 2, a 3,... van positieve gehele getallen. Bepaal de kleinst mogelijke waarde van a 2010 als gegeven is: (i) a n < a n+1 voor alle n 1, (ii)
Meten en experimenteren
 Meten en experimenteren Statistische verwerking van gegevens Een korte inleiding 6 oktober 009 Catherine De Clercq Statistische verwerking van gegevens Kursus statistiek voor fysici door Jorgen D Hondt
Meten en experimenteren Statistische verwerking van gegevens Een korte inleiding 6 oktober 009 Catherine De Clercq Statistische verwerking van gegevens Kursus statistiek voor fysici door Jorgen D Hondt
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 2008 Limieten en asymptoten van rationale functies (versie juli 2008) Rationale functies. Inleiding Functies als f : 5 5, f 2 : 2 3 + 2 f 3 : 32 + 7 4 en f 4 :
Katholieke Universiteit Leuven September 2008 Limieten en asymptoten van rationale functies (versie juli 2008) Rationale functies. Inleiding Functies als f : 5 5, f 2 : 2 3 + 2 f 3 : 32 + 7 4 en f 4 :
Experimenteel onderzoek
 Newton - VWO Experimenteel onderzoek Samenvatting Soorten onderzoek experimenteel onderzoek - de opzet van een experimenteel onderzoek hangt af van het onderzoeksdoel literatuuronderzoek - over een bepaald
Newton - VWO Experimenteel onderzoek Samenvatting Soorten onderzoek experimenteel onderzoek - de opzet van een experimenteel onderzoek hangt af van het onderzoeksdoel literatuuronderzoek - over een bepaald
Combinatorische Algoritmen: Binary Decision Diagrams, Deel III
 Combinatorische Algoritmen: Binary Decision Diagrams, Deel III Sjoerd van Egmond LIACS, Leiden University, The Netherlands svegmond@liacs.nl 2 juni 2010 Samenvatting Deze notitie beschrijft een nederlandse
Combinatorische Algoritmen: Binary Decision Diagrams, Deel III Sjoerd van Egmond LIACS, Leiden University, The Netherlands svegmond@liacs.nl 2 juni 2010 Samenvatting Deze notitie beschrijft een nederlandse
1.1 Lineaire vergelijkingen [1]
![1.1 Lineaire vergelijkingen [1] 1.1 Lineaire vergelijkingen [1]](/thumbs/62/47724253.jpg) 1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
Meting zonnepaneel. Voorbeeld berekening diodefactor: ( ) Als voorbeeld wordt deze formule uitgewerkt bij een spanning van 7 V en 0,76 A:
 Meting zonnepaneel Om de beste overbrengingsverhouding te berekenen, moet de diodefactor van het zonnepaneel gekend zijn. Deze wordt bepaald door het zonnepaneel te schakelen aan een weerstand. Een multimeter
Meting zonnepaneel Om de beste overbrengingsverhouding te berekenen, moet de diodefactor van het zonnepaneel gekend zijn. Deze wordt bepaald door het zonnepaneel te schakelen aan een weerstand. Een multimeter
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: functieverloop. 22 juli 2015. dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: functieverloop 22 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: functieverloop 22 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Calculus I, 23/11/2015
 Calculus I, /11/015 1. Beschouw de functie met a, b R 0. f = a + b + lne a Benoem het domein van de functie f. b Bepaal a en b zodat de rechte y = 1 een schuine asymptoot is voor f. c Voor a = en b = 1,
Calculus I, /11/015 1. Beschouw de functie met a, b R 0. f = a + b + lne a Benoem het domein van de functie f. b Bepaal a en b zodat de rechte y = 1 een schuine asymptoot is voor f. c Voor a = en b = 1,
Tentamen Simulaties van Biochemische Systemen - 8C110 en 8CB19 4 Juli uur
 Tentamen Simulaties van Biochemische Systemen - 8C0 en 8CB9 4 Juli 04-900-00 uur Vier algemene opmerkingen: Het tentamen bestaat uit 7 opgaven verdeeld over pagina s Op pagina 4 staat voor iedere opgave
Tentamen Simulaties van Biochemische Systemen - 8C0 en 8CB9 4 Juli 04-900-00 uur Vier algemene opmerkingen: Het tentamen bestaat uit 7 opgaven verdeeld over pagina s Op pagina 4 staat voor iedere opgave
Oplossing 1de deelexamen Calculus II van 29/2/2012
 Oplossing 1de deelexamen Calculus II van 9//1 March 6, 1 1 raag 1 Beschouw de volgende kromme in R 3, geparametriseerd als r(t) = ti + (t 1)j + t k. (a) Als de parameter t een tijd aangeeft, bereken dan
Oplossing 1de deelexamen Calculus II van 9//1 March 6, 1 1 raag 1 Beschouw de volgende kromme in R 3, geparametriseerd als r(t) = ti + (t 1)j + t k. (a) Als de parameter t een tijd aangeeft, bereken dan
Meten en experimenteren
 Meten en experimenteren Statistische verwerking van gegevens Een korte inleiding 3 oktober 006 Deel I Toevallige veranderlijken Steekproef Beschrijving van gegevens Histogram Gemiddelde en standaarddeviatie
Meten en experimenteren Statistische verwerking van gegevens Een korte inleiding 3 oktober 006 Deel I Toevallige veranderlijken Steekproef Beschrijving van gegevens Histogram Gemiddelde en standaarddeviatie
Hoofdstuk A9 Hellinggrafieken - alternatief
 Hoofdstuk A9 Hellinggrafieken - alternatief Hellinggrafieken a. Maak instap opgaven I-a en I-b (zonder de formules van instap opgave I- te gebruiken). snelheid (m/s) tijd (seconden) b. Hoe kun je met de
Hoofdstuk A9 Hellinggrafieken - alternatief Hellinggrafieken a. Maak instap opgaven I-a en I-b (zonder de formules van instap opgave I- te gebruiken). snelheid (m/s) tijd (seconden) b. Hoe kun je met de
3.1 Haakjes wegwerken [1]
![3.1 Haakjes wegwerken [1] 3.1 Haakjes wegwerken [1]](/thumbs/53/31611347.jpg) 3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
Auto-antennes. Tim Weenink ( ) & Omar Richardson ( )
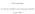 Auto-antennes Tim Weenink (0775602) & Omar Richardson (0675453) 25 maart 2013 Inhoudsopgave 1 Samenvatting 2 2 Probleembeschrijving 3 3 Model 5 4 Berekeningen 6 5 Resultaten 7 6 Plannen voor verder onderzoek
Auto-antennes Tim Weenink (0775602) & Omar Richardson (0675453) 25 maart 2013 Inhoudsopgave 1 Samenvatting 2 2 Probleembeschrijving 3 3 Model 5 4 Berekeningen 6 5 Resultaten 7 6 Plannen voor verder onderzoek
2IV10 Oefentoets uitwerking
 2IV10 Oefentoets uitwerking Deze oefentoets bestaat uit drie opgaven, waarvoor twee uur beschikbaar is. Bij voldoende resultaat wordt een bonuspunt toegekend voor het tentamen. De opgaven betreffen een
2IV10 Oefentoets uitwerking Deze oefentoets bestaat uit drie opgaven, waarvoor twee uur beschikbaar is. Bij voldoende resultaat wordt een bonuspunt toegekend voor het tentamen. De opgaven betreffen een
Zomercursus Wiskunde. Module 4 Limieten en asymptoten van rationale functies (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 20 Module 4 Limieten en asymptoten van rationale functies (versie 22 augustus 20) Inhoudsopgave Rationale functies. Inleiding....................................2
Katholieke Universiteit Leuven September 20 Module 4 Limieten en asymptoten van rationale functies (versie 22 augustus 20) Inhoudsopgave Rationale functies. Inleiding....................................2
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking van het tentamen Functietheorie (2Y480) op ,
 1 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking van het tentamen Functietheorie (2Y480) op 25-11-1998, 9.00-12.00 uur Opgave 1 1. Formuleer de Cauchy-Riemann-vergelijkingen.
1 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking van het tentamen Functietheorie (2Y480) op 25-11-1998, 9.00-12.00 uur Opgave 1 1. Formuleer de Cauchy-Riemann-vergelijkingen.
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Snelle glijbanen. Masterclass VWO-leerlingen juni Emiel van Elderen en Joost de Groot NWD Faculteit EWI, Toegepaste Wiskunde
 Masterclass VWO-leerlingen juni 2008 Snelle glijbanen Emiel van Elderen en Joost de Groot NWD 2009 1 Technische Universiteit Delft Probleemstelling Gegeven: een punt A(0,a) en een punt B(b, 0) met a 0.
Masterclass VWO-leerlingen juni 2008 Snelle glijbanen Emiel van Elderen en Joost de Groot NWD 2009 1 Technische Universiteit Delft Probleemstelling Gegeven: een punt A(0,a) en een punt B(b, 0) met a 0.
1.0 Voorkennis. Voorbeeld 1: Los op: 6x + 28 = 30 10x.
 1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
