Noorderpoortcollege school voor MBO Stadskanaal. Reader. Wiskunde MBO Niveau 4 periode 3. M. van der Pijl. Transfer Database

Transcriptie

1 Noorderpoortcollege school voor MBO Stadskanaal Reader Wiskunde MBO Niveau 4 periode 3 M. van der Pijl Transfer Database

2 ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet Onderwijs, Beroepsonderwijs en Volwasseneneducatie en Hoger Beroepsonderwijs. Meer informatie over ThiemeMeulenhoff en een overzicht van onze leermiddelen: of via onze klantenservice (088) ThiemeMeulenhoff, Amersfoort, 013. Alle rechten voorbehouden. Niets uit deze uitgave mag worden verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm of op enige wijze, hetzij elektronisch, mechanisch, door fotokopieën, opnamen, of enig andere manier, zonder voorafgaande schriftelijke toestemming van de uitgever. Voor zover het maken van kopieën uit deze uitgave is toegestaan op grond van artikel 16 Auteurswet j o het Besluit van 3 augustus 1985, Stbl., dient men de daarvoor wettelijk verschuldigde vergoedingen te voldoen aan Stichting Publicatie- en Reproductierechten Organisatie (PRO), Postbus 3060, 130 KB Hoofddorp ( Voor het overnemen van gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16 Auteurswet 191) dient men zich tot de uitgever te wenden. Voor meer informatie over het gebruik van muziek, film en het maken van kopieën in het onderwijs zie De uitgever heeft ernaar gestreefd de auteursrechten te regelen volgens de wettelijke bepalingen. Degenen die desondanks menen zekere rechten te kunnen doen gelden, kunnen zich alsnog tot de uitgever wenden.

3 1 Wetenschappelijke en technische notatie Rekenen met machten van Drijvende komma notatie Wetenschappelijke notatie Technische notatie 7 Rekenen met machten en lettergetallen 1.1 Werken met machten 1. Vermenigvuldigen en delen van machten met hetzelfde grondtal 13.3 Werken met wortels 14.4 Vereenvoudigen van uitdrukkingen met letters 15.5 Haakjes wegwerken 17.6 Werken met formules 19 3 Tekenen en aflezen van tweedegraads grafieken Tekenen van tweedegraads grafieken 5 3. Minimum, maximum en symmetrieas Berekening nulpunten Steilheid van tweedegraads grafieken 3 4 Oplossen van tweedegraads vergelijkingen De abc-formule De abc-formule en de symmetrieas De abc-formule en de nulpunten Het functieonderzoek en het tekenen van de grafiek 46

4

5 1 Wetenschappelijke en technische notatie 1 Rekenen met machten van 10 Omdat de wetenschappelijke en technische notatie machten van 10 bevatten, besteden we eerst aandacht aan de rekenregels voor machten. Vermenigvuldigen en delen van machten Machtsverheffen is een verkorte manier voor het vermenigvuldigen: = 10 = In de macht 10 4 noemen we 10 het grondtal en 4 de exponent. De exponent geeft het aantal keren aan dat het grondtal met zichzelf vermenigvuldigd is. Als we 10-machten met elkaar vermenigvuldigen, mogen we de exponenten optellen: = 10 = 10 Immers: = 10 7 Vb. 1 Bereken Uitwerking = = 10 + = Oefeningen 1 Zet om naar 10 -macht: a b ThiemeMeulenhoff 16 januari 013

6 Wetenschappelijke en technische notatie c d e We kunnen dus machten met hetzelfde grondtal vermenigvuldigen door hun exponenten op te tellen. We weten dat delen de omkeerbewerking is van vermenigvuldigen. Ook geldt dat aftrekken de omkeerbewerking van optellen is. We gaan nu bekijken of we machten kunnen delen door de exponenten van elkaar af te trekken. Vb Uitwerking = = 3 = 10 1 = 10 Oefeningen Zet om naar 10 -macht: a b c d e ThiemeMeulenhoff 16 januari 013

7 Wetenschappelijke en technische notatie 3 We bekijken nog eens oefening e: = 10 = 10 Bij het optellen en aftrekken van exponenten gelden de gewone voorrangsregels. Bij machtsverheffen gebruiken we de volgende regels: a b a+ b = 10 a b a b = 10 a b a b ( 10 ) = = 1 1 a = 10 a 10 3 Zet om naar 10 -macht: a b c d ( 10 ) e ( 10 ) ( 10 ) 5 5 f ( 10 ) ( 10 ) Vb. 3 Schrijf de volgende machten eerst als breuk met een 10 -macht in de noemer en vervolgens als gewone breuk:10 5 Uitwerking = = ThiemeMeulenhoff 16 januari 013

8 4 Wetenschappelijke en technische notatie 4 Schrijf de volgende machten eerst als breuk met een 10 -macht in de noemer en vervolgens als gewone breuk: a 10 b 10 3 c 10 1 d 10 1 e 10 6 f 10 9 Drijvende komma notatie Als we met onze rekenmachine 87, , 34 uitrekenen, krijgen we als uitkomst , Dat antwoord staat in de zogenaamde drijvende komma notatie. Zo kunnen we ook 6, , 76 uitrekenen; de uitkomst hiervan is 0, Naast de drijvende komma notatie kennen we ook de wetenschappelijke notatie en de technische notatie. ThiemeMeulenhoff 16 januari 013

9 Wetenschappelijke en technische notatie 5 3 Wetenschappelijke notatie In de natuurkunde en in de techniek werken we veel met machten van 10 om heel grote en heel kleine getallen weer te geven. Vb. 4 We willen een groot getal als met een macht van 10 schrijven. Als we in gedachten de komma tussen de 4 en de 6 plaatsen en het aantal cijfers achter de komma tellen, komen we uit op 11. We hebben de komma dus 11 plaatsen naar links geschoven. dit betekent een exponent van +11. We kunnen het getal daarom noteren als 4, Op veel rekenmachines wordt dit weergegeven als 4, 68E 11. Zo kunnen we ook heel kleine getallen schrijven met een macht van 10, we nemen als voorbeeld het getal 0, Als we in gedachten de komma tussen de 1 en de plaatsen en tellen hoeveel plaatsen de komma naar rechts schuift, komen we uit op 5. Dat betekent een exponent van 5 (negatief!). We kunnen het getal 0, daarom noteren als 1, De meeste rekenmachines geven dit weer als 1, E 5. Deze methode van noteren van heel grote en heel kleine getallen noemen we de wetenschappelijke notatie. We spreken ook wel van de SCI-notatie, afgeleid van het Engels: SCIentific notation. Vb We kunnen 1, 3 10, 5 10 uitrekenen door 1, 3, 5 en daarna uit te rekenen , 3, 5 = 3, 5 en = 10 = 10, dus 6 4 1, 3 10, 5 10 = 3, We kunnen dit ook in één bewerking met de rekenmachine berekenen. Reken machines hebben voor dit doel een speciale toets EE of EXP, afhankelijk van het merk. We moeten dan het volgende intypen: [ 1, 3 ] [ 6 ] [, 5 ] [ 4 ]. 5 Schrijf de volgende getallen in de wetenschappelijke notatie: a b c ThiemeMeulenhoff 16 januari 013

10 6 Wetenschappelijke en technische notatie d e f Schrijf de volgende getallen in de wetenschappelijke notatie: a 0, b 0, c 0, d 0, 004 e 0, f 0, De snelheid van het licht is 3, m/s. Het licht van een ster doet er 3 jaar over om de aarde te bereiken. Hoeveel kilometer is de ster van de aarde verwijderd? Voor het verband tussen de afgelegde weg s, de snelheid v en de tijd t geldt de formule: s = v t. ThiemeMeulenhoff 16 januari 013

11 Wetenschappelijke en technische notatie 7 4 Technische notatie Bij de technische notatie worden net als bij de wetenschappelijke notatie getallen met een macht van 10 geschreven. Alleen zijn de exponenten altijd veelvouden van 3, dus van klein naar groot: , 10, 10, 10, 10, 10, 10, 10, 10,... Bij de technische notatie kunnen 1, of 3 cijfers voor de komma staan: 0, = 1, 10 6 ;. 750 =, , = ; = 7, , 0001 = ; = De meeste CASIO-rekenmachines hebben een -toets (ENG = ENGineer). Als we daarop klikken wordt, het getal omgezet van de wetenschappelijke notatie in de technische notatie. Als we nogmaals op deze toets klikken, wordt de exponent met 3 verlaagd. Met de combinatie + verhogen we de exponent met 3. 8 Schrijf de volgende getallen in de technische notatie: a b c d e f ThiemeMeulenhoff 16 januari 013

12 8 Wetenschappelijke en technische notatie 9 Schrijf de volgende getallen in de technische notatie: a 0, b 0, c 0, d 0, 004 e 0, f 0, Schrijf de volgende getallen eerst in de wetenschappelijke en daarna in de technische notatie: a b c 0, d 0, 0005 ThiemeMeulenhoff 16 januari 013

13 Wetenschappelijke en technische notatie 9 11 Geef de uitkomsten van de volgende berekeningen in de technische notatie: a 3, , b, , c 8, , Een bolvormige bacterie heeft een diameter van 1, m. π 3 Voor het volume van een bol geldt de formule: V = d 6 Bereken het volume van de bacterie. Geef de uitkomst zowel in de wetenschappelijke als in de technische notatie. 13 De diameter van de aarde is 1, m. a Bereken het volume van de aarde. Geef de uitkomst zowel in de wetenschappelijke als in de technische notatie. b Hoeveel keer is het volume van de aarde groter dan het volume van de bacterie uit de vorige opgave? Geef de uitkomst zowel in de wetenschappelijke als in de technische notatie. 14 Met de Wet van Hooke kunnen we de verlenging berekenen van een draad waaraan getrokken wordt. F l De Wet van Hooke luidt: l = E A Voor een koperdraad geldt: l =, 0 m F = N, E = N/m en A = 10 6 m. Bereken de verlenging l. Geef het antwoord zowel in de drijvende komma notatie, in de wetenschappelijke notatie en in de technische notatie. ThiemeMeulenhoff 16 januari 013

14 10 Wetenschappelijke en technische notatie Antwoorden 1a 10 3 b 10 5 c 10 9 d 10 9 e 10 1 a 10 b 10 c 10 3 d 10 e a 10 0 = 1 b 10 c 10 7 d 10 9 e 10 6 f 10 0 = 1 4a b c d e f = = = = = = a 8, b 1, c 3, d 4, 10 9 e 6, f 5, a 8, b 1, c 3, d 4, 10 3 e 6, f 5, ThiemeMeulenhoff 16 januari 013

15 Wetenschappelijke en technische notatie 11 7, km 8a 8, b 1, c d 4, 10 9 e f a b 1, c d 4, 10 3 e f a, ; 3, b 8, ; c 9, ; d, ; a 15, b 45, c 3, , m a 1, 1 10 m ; 1, b 6, 0 10 ; , 0153 = 1, m = 15, 3 10 m m ThiemeMeulenhoff 16 januari 013

16 Rekenen met machten en lettergetallen 1 Werken met machten Als we twee dezelfde getallen met elkaar vermenigvuldigen, is dat hetzelfde als kwadrateren. Als het gaat om meer dan twee dezelfde getallen, spreken we van machtsverheffen. Vb = 5 = 5 Rekenmachine: x antwoord 5 Vb = ( 7) = Rekenmachine: - antwoord 401 Vb. 3 7 = = 18 Rekenmachine: = antwoord 401 In de macht 7 noemen we het getal het grondtal van deze macht. Het getal 7 heet de exponent van de macht. Oefeningen 1 Bereken de volgende machten: a 4 5 ThiemeMeulenhoff 16 januari 013

17 Rekenen met machten en lettergetallen 13 b 5 3 c ( 3) 5 d 9 3 e ( 4) 5 f 0 9 g 1 1 Vermenigvuldigen en delen van machten met hetzelfde grondtal Als we machten met hetzelfde grondtal met elkaar vermenigvuldigen, krijgen we een macht met hetzelfde grondtal en als exponent de som van de oorspronkelijke exponenten. Vb = ( ) ( 3 3) = 3 ( + = ) Als we machten met hetzelfde grondtal door elkaar delen, krijgen we een macht met hetzelfde grondtal en als exponent het verschil van de oorspronkelijke exponenten. Vb = = = 4 ( = ) ThiemeMeulenhoff 16 januari 013

18 14 Rekenen met machten en lettergetallen Denk erom: = 1, omdat bijvoorbeeld 3 3 = = = Maar ook geldt: 3 3 = 3 = 3, dus 3 0 = 1. In het algemeen geldt dat een willekeurig getal tot de nulde macht 1 is (behalve 0 0 ). 5 Vb a a a = a = a Oefeningen Bereken: a b c d d d d x x x 6 5 e f y y y 3 Werken met wortels Worteltrekken is de omgekeerde bewerking van kwadrateren. Vb. 7 = eigenlijk een tweede- 36 = 6, want 6 36 We bedenken daarbij dat onze gewone wortel machtswortel is. ThiemeMeulenhoff 16 januari 013

19 Rekenen met machten en lettergetallen 15 Zo kennen we ook de hogeremachtswortel. Dit is de omgekeerde bewerking van hogere machten. Vb = 3, want 3 3 = 7 CASIOfx 8 : TI 30 : Oefeningen 3 Bereken: a b 16 4 c 81 3 d 1 e 3 a 3 f 3 d 6 4 Vereenvoudigen van uitdrukkingen met letters Uitdrukkingen waarin letters voorkomen, noemen we algebraïsche vormen. 7 4 Een voorbeeld hiervan is 4t 4x y + 1a b. Een groep letters, al dan niet vergezeld van cijfers, heet een term. Een voorbeeld hiervan is 8x 5 y 3. ThiemeMeulenhoff 16 januari 013

20 16 Rekenen met machten en lettergetallen Een term is vaak een vermenigvuldiging (ook wel product genoemd) van meerdere factoren. Termen kunnen we bij optellen en aftrekken alleen vereenvoudigen als deze termen gelijksoortig zijn. Vb. 9 6a + 9a = ( 6 + 9) a = 15a ( 6a en 9a zijn gelijksoortig) Vb. 10 6a + 9b blijft 6a + 9b ( 6a en 9b zijn niet gelijksoortig, dus vereenvoudiging is niet mogelijk) Vb. 11 7a b 5a b = ( 7 5) a b = a b Vb. 1 5x 3y x + y = ( 5 ) x + ( 3 + ) y = 3x y Oefeningen 4 Vereenvoudig: a p 5p b 3a + 4a + a c 3pq + pq 5pq d x + ( 3x ) 3 3 e 7ab + ( 3ab ) f 4a 3b 5b a ThiemeMeulenhoff 16 januari 013

21 Rekenen met machten en lettergetallen g xy 3x y + 5x y 4xy h 3a 6ab + a + a 3ab 5 Haakjes wegwerken Nu gaan we ééntermen (zoals 3, 5b of 8g 3 ) vermenigvuldigen met tweetermen (zoals 3 + 6c of 6 5s ), en twee tweetermen met elkaar vermenigvuldigen. We moeten dan haakjes wegwerken. Vb. 13 3( a 4) = 3 a = 3a 1 Vb. 14 b( 3a + 4b 5c) = b 3a + b 4b + b 5c = 6ab + 8b 10bc Vb. 15 ( a + 3)( b + 7) = a( b + 7) + 3( b + 7) = a b + a b = ab + 7a + 3b + 1 Vb. 16 ( x 1)( x + ) = x( x + ) 1( x + ) = x x + x 1 x 1 = x + x x = x + x Oefeningen 5 Werk de haakjes weg: a a( 6 + p) b ap( a p) 3 c 3s ( s 4s) ThiemeMeulenhoff 16 januari 013

22 18 Rekenen met machten en lettergetallen d ( a b)( c d) e ( 6p + 4w)( 7g + 5h) f ( x x )( 4x + 3x ) g ( 3a 7)( a + 5) h ( 1 y)( 1 + 4y ) i ( x + 3)( x + ) j ( x 3)( x + 11) k ( x 6)( x 10) l ( 3a + 7)( 3a 1) m ( x + 6)( x 9) n ( x + 5)( x 5) ThiemeMeulenhoff 16 januari 013

23 Rekenen met machten en lettergetallen 19 o ( x 3) p ( x + 7) 6 Werken met formules Als we een berekening moeten maken waarbij we gebruik maken van een formule, hebben we soms tussenstappen nodig om tot het antwoord te komen. Bij de laatste stap van onze berekening moeten we gebruik maken van omkeerbewerking. De omkeerbewerking van optellen is aftrekken. De omkeerbewerking van aftrekken is optellen. De omkeerbewerking van vermenigvuldigen is delen. De omkeerbewerking van delen is vermenigvuldigen. De omkeerbewerking van een macht is de wortel. De omkeerbewerking van de wortel is de macht. Eerst gaan we berekeningen uitvoeren met eenvoudige formules. Vb. 16 Gegeven De formule l = l0 α T met α = K 1, l = 6mm en T = 50 K. Gevraagd l 0 in meters. Oplossing Eerst moeten we de eenheden controleren. De uitkomst wordt gevraagd in meters, terwijl l in millimeters wordt opgegeven, dus l = 6mm = m. Nu kunnen we de formule invullen: l = l α T 6 10 m = l 1 10 K 50 K = l l0 = = 10 m ThiemeMeulenhoff 16 januari 013

24 0 Rekenen met machten en lettergetallen Oefeningen 3 6a Bereken ρ in kg/m 3 als V = 3, 5dm en m = 31, 15kg met de formule m = ρ V. b Bereken m in kg met Epot = m g h als E pot = 147 Nm, g = 9, 8 N/kg en h = 50cm. c Bereken r in m als F = 100 N en M = 900 Nm met de formule M = F r. d U = E I R. Bereken I in A als U k = 4, 5 V, E = 5 V en R i = 1, 5Ω. k i Nu gaan we werken met formules waarmee moeilijker is te rekenen. Vb. 17 Gegeven m T = π met T = s en c = 80kg/s c Gevraagd Bereken m in kg. Oplossing T T m = π gaan we met vermenigvuldigingstekens noteren als c m = π en daarna invullen: c s = m π 80 kg/s m = 6, 8 80 (links en rechts delen door 6, 8 ) m 0, 3 = (links en rechts kwadrateren om de wortel kwijt te raken) 80 ( 0, 3) = m 80 m 0, 10 = 80 m = 80 0, 10 = 8 kg ThiemeMeulenhoff 16 januari 013

25 Rekenen met machten en lettergetallen 1 Oefeningen 7 σ = 5 F b met σ in kn/mm, F in kn, 3 b en d in mm. d a Bereken σ in kn/mm als F = 45kN, b =, 5mm en d = 1, 5cm. b F = 0kN, σ = kn/mm en d = 9mm. Bereken b in mm. c σ = 7 kn/mm, b = 1, 8 cm en d =, 5cm. Bereken F in kn. d F = 10kN, σ = 1, 17kN/mm en b = 1mm. Bereken d in mm. π E I 8 Fk = met F k in kn, E in kn/cm, I in cm 4 en L k in cm Lk 4 4 a E = 5, 10 kn/cm, I = 44, 7cm en L k = 45mm. Bereken F k in kn. b Fk = 60kN, E =, kn/cm en L k = 5cm. Bereken I in cm c E = 4, 5 10 kn/cm, I = 30, 5 10 cm en F k = 100 N. Bereken L k in cm. 9 vgem = k g h a k = 1, 4, g = 9, 81m/s en h = 15, 5m. Bereken v gem in m/s. b vgem = 14 m/s, g = 9, 81m/s en k = 1, 8. Bereken h in m. ThiemeMeulenhoff 16 januari 013

26 Rekenen met machten en lettergetallen c Bereken k als vgem = 14 m/s, h = 10 m en g = 9, 81 m/s. P 10 d = 46, 3 4 met d in mm, P in kw en n in omw/s. n a Bereken d als P = 30kW en n = omw/s. b d = 10cm en n = 60omw/min. Bereken P. c P = 3500 W en d = 45mm. Bereken n. ThiemeMeulenhoff 16 januari 013

27 Rekenen met machten en lettergetallen 3 Antwoorden 1a 104 b c 43 d 79 e 104 f 0 g 1 a 3 3 b 4 c d d x e 7 f 1 3a 13 b 6 c 3 d, 9 e a f d 4a 3p b 8 a c 6pq d x e 4ab 3 f 6a 8b g xy 3 + x 3 y h a 9ab a 5a 6a + ap b a p 4ap 5 3 c 6s 1s d ac ad bc + bd e 4pg + 30ph + 8wg + 0wh ThiemeMeulenhoff 16 januari 013

28 4 Rekenen met machten en lettergetallen f 4x + 3x + 8x 6x g 6a a 35 3 h 1 + 4y + y 4y i x + 5x + 6 j x + 8x 33 k x 16x + 60 l 9a + 18a 7 m 4x 6x 54 n x 5 o x 6x + 9 p x + 14x a 8, kg/m 3 b 30kg c 0, 75Ω d 0, 33A 7a 1, 5 kn/mm b 14, 6 mm c 115, 3kN d 8 mm 8a 113, 9kN b 7, cm 4 c 0, 3cm 9a 4, 8 m/s b 6m c 1 10a 91, 1mm b 1, 8kW c 3, 9omw/s ThiemeMeulenhoff 16 januari 013

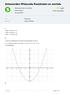
29 3 Tekenen en aflezen van tweedegraads grafieken 1 Tekenen van tweedegraads grafieken Een grafiek van bijvoorbeeld de functie y = x is een tweedegraads verband of anders gezegd een tweedegraads functie. We kunnen deze ook noteren als f( x) = x. We kunnen door de coördinaten van een aantal punten uit te rekenen een grafiek van een functie tekenen. Hiertoe berekenen we voor een aantal waarden voor x de bijbehorende waarden voor y. Vb. 1 Teken de grafiek van y = x. Oplossing x = : y = x y = ( ) = 4 (denk om haakjes bij het gebruik van de rekenmachine) x = 1 : y = x y = ( 1) = 1 x = 0 : y = x y = 0 = 0 x = 1 : y = x y = 1 = 1 x = : y = x y = = 4 Vervolgens verzamelen we deze waarden van x en y in een tabel: x y Tabel 1 ThiemeMeulenhoff 16 januari 013

30 6 Tekenen en aflezen van tweedegraads grafieken Ten slotte tekenen we deze punten in een assenstelsel en verbinden ze met elkaar door een vloeiende lijn. Zie figuur 1. y x Figuur 1 Zo n grafiek van een tweedegraads functie noemen we een parabool. Een parabool heeft altijd een symmetrieas. De grafiekgedeelten links en rechts van deze symmetrieas zijn elkaars spiegelbeeld. Oefeningen 1 Teken de grafiek van: a y = x 1 ThiemeMeulenhoff 16 januari 013

31 Tekenen en aflezen van tweedegraads grafieken 7 b y = x + c y = x 3 d y = x ThiemeMeulenhoff 16 januari 013

32 8 Tekenen en aflezen van tweedegraads grafieken Teken de grafiek van: a y = x + 1, 5 b y = x 4 c y = x + 4 ThiemeMeulenhoff 16 januari 013

33 Tekenen en aflezen van tweedegraads grafieken 9 d y = x 1, 5 Minimum, maximum en symmetrieas Bij voorbeeld 1 en bij de oefeningen 1 en hebben we gezien dat er twee mogelijkheden zijn. Een parabool kan de vorm hebben van een dal of van een berg. De eerste noemen we een dalparabool en de tweede een bergparabool. Bij een dalparabool vinden we een minimum en bij een bergparabool een maximum. Als we te maken hebben met een functie van de vorm y = x + c, is er sprake van een dalparabool met een minimum. De symmetrieas is x = 0 en het minimum kunnen we uit rekenen door x = 0 in te vullen. Voor y vinden we de waarde c, dus het minimum heeft de coördinaten ( 0, c ). Hebben we te maken met een functie met de vorm y = x + c, dan is er sprake van een bergparabool met een maximum. De symmetrieas is x = 0 en het minimum kunnen we uitrekenen door x = 0 in te vullen. Voor y vinden we de waarde c, dus het maximum heeft de coördinaten ( 0, c ). Vb. Gegeven De functie f( x) = x + 3, 5 Gevraagd Bepaal of er sprake is van een maximum of een minimum. Bereken het minimum of maximum. Bepaal de plaats van de symmetrieas. Oplossing f( x) is een bergparabool, dus er is sprake van een maximum. f( x) = y = x + 3, 5 ; voor x = 0 is y = 0 + 3, 5 = 3, 5 maximum: ( 0, 3, 5 ). symmetrieas: x = 0 ThiemeMeulenhoff 16 januari 013

34 30 Tekenen en aflezen van tweedegraads grafieken 3 Bereken het minimum of maximum en bepaal de symmetrieas van de grafieken van de volgende formules. a y = x 1 b y = x + c y = x 3 d y = x e y = x + 1, 5 f y = x 4 g y = x + 4 h y = x 1, 5 3 Berekening nulpunten In oefening 3 zien we dat het maximum of het minimum berekend kan worden door voor x de waarde 0 in te vullen. Een aantal grafieken doorsnijdt de x-as, we noemen dit de nulpunten. We kunnen deze nulpunten berekenen door voor y de waarde 0 in te vullen. ThiemeMeulenhoff 16 januari 013

35 Tekenen en aflezen van tweedegraads grafieken 31 Vb. 3 Bereken de nulpunten van de grafiek van y = x 3. Oplossing x 3 = 0 x = x = 3 x = 3 = 1, 7of x = 3 = 1, 7 Nulpunten: ( 1, 7, 0 ) en ( 1, 7, 0) 4 Bereken het minimum of maximum, bereken eventueel de nulpunt(en), schrijf de symmetrieas op en teken de grafiek. a f( x) = x 9 b f( x) = x 4 c y = x d y = x Bereken het minimum of maximum, bereken eventueel de nulpunt(en), schrijf de symmetrieas op en teken de grafiek. a y = x b y = x + 3 c y = x + 5 d f( x) = x 1 ThiemeMeulenhoff 16 januari 013

36 3 Tekenen en aflezen van tweedegraads grafieken 4 Steilheid van tweedegraads grafieken We zien dat in de grafiek van y = x + c of y = x + c de waarde van c de verschuiving op de y-as is. Nu gaan we de grafiek van y = ax + c bekijken. Voor a kunnen we een wille keurig getal invullen. Als voorbeeld nemen we de grafieken van de functies y = x en y = x. Eerst berekenen we weer voor een aantal waarden voor x de bijbehorende waarden voor y. x y = x y = Tabel x In onderstaand diagram hebben we de grafieken getekend van y = x en y x Zie figuur. = y 5 x Figuur x x We zien dat de grafiek van y = x steiler is dan de grafiek van y = x. In het algemeen kunnen we stellen dat de grafiek van y = a x steiler wordt als a groter wordt. Vb. 4 Gegeven y = x 8 Gevraagd Bereken het minimum of maximum, bereken eventueel de nulpunt(en), schrijf de symmetrieas op en teken de grafiek. ThiemeMeulenhoff 16 januari 013

37 Tekenen en aflezen van tweedegraads grafieken 33 Oplossing Symmetrieas: x = 0 Minimum: y = 0 8 = 8 ( 0, 8) Nulpunten: x 8 = 0 x = x = 8 x 8 = = 4 x = 4 = of x = 4 = (, 0) en (, 0) We maken een tabel met de bij elkaar horende waarden van x en y. x 0 y Tabel 3 y x Figuur 3 6 Bereken het minimum of maximum, bereken eventueel de nulpunt(en), schrijf de symmetrieas op en teken de grafiek. a y = x ThiemeMeulenhoff 16 januari 013

38 34 Tekenen en aflezen van tweedegraads grafieken 1 b f( x) = x c y = 3x 3 7 Bereken het minimum of maximum, bereken eventueel de nulpunt(en), schrijf de symmetrieas op en teken de grafiek. a f( x) = x + 8 ThiemeMeulenhoff 16 januari 013

39 Tekenen en aflezen van tweedegraads grafieken 35 b y = 1, 5x + 6 c y =, 5x 7, 5 d y = 0, 5x 4, 5 ThiemeMeulenhoff 16 januari 013

40 36 Tekenen en aflezen van tweedegraads grafieken Antwoorden 1a We maken een tabel met de bij elkaar horende waarden van x en y. x y Tabel 4 y x Figuur 4 b We maken een tabel met de bij elkaar horende waarden van x en y. x y Tabel 5 y x Figuur 5 ThiemeMeulenhoff 16 januari 013

41 Tekenen en aflezen van tweedegraads grafieken 37 c We maken een tabel met de bij elkaar horende waarden van x en y. x y tabel 6 y x Figuur 6 d We maken een tabel met de bij elkaar horende waarden van x en y. x y Tabel 7 y Figuur 7 x ThiemeMeulenhoff 16 januari 013

42 38 Tekenen en aflezen van tweedegraads grafieken a We maken een tabel met de bij elkaar horende waarden van x en y. x y Tabel 8 y x Figuur 8 b We maken een tabel met de bij elkaar horende waarden van x en y. x y Tabel 9 y Figuur 9 x ThiemeMeulenhoff 16 januari 013

43 Tekenen en aflezen van tweedegraads grafieken 39 c We maken een tabel met de bij elkaar horende waarden van x en y. x y Tabel 10 y x Figuur 10 d We maken een tabel met de bij elkaar horende waarden van x en y. x y 5,5,5 1,5,5 5,5 Tabel 11 y x Figuur 11 3a minimum ( 0, 1) ; symmetrieas: x = 0 b minimum ( 0, ) ; symmetrieas: x = 0 ThiemeMeulenhoff 16 januari 013

44 40 Tekenen en aflezen van tweedegraads grafieken c minimum ( 0, 3 ) ; symmetrieas: x = 0 d maximum ( 0, 0 ) ; symmetrieas: x = 0 e minimum ( 0, 1, 5 ) ; symmetrieas: x = 0 f minimum ( 0, 4 ); symmetrieas: x = 0 g maximum ( 0, 4 ) ; symmetrieas: x = 0 h maximum ( 0, 1, 5) ; symmetrieas: x = 0 4a minimum ( 0, 9) ; symmetrieas: x = 0 ; nulpunten: ( 3, 0 ) en ( 3, 0) b minimum ( 0, 4) ; symmetrieas: x = 0 ; nulpunten: (, 0 ) en (, 0) c minimum ( 0, ) ; symmetrieas: x = 0 ; nulpunten: ( 1, 4, 0 ) en ( 1, 4, 0) d minimum ( 0, 3 ) ; symmetrieas: x = 0 ; geen nulpunten 5a maximum ( 0, 0 ) ; symmetrieas: x = 0 ; nulpunt ( 0, 0) b maximum ( 0, 3 ) ; symmetrieas: x = 0 ; nulpunten: ( 1, 7, 0 ) en ( 1, 7, 0) c maximum ( 0, 5 ) ; symmetrieas: x = 0 ; nulpunten: (,, 0 ) en (,, 0) d maximum ( 0, 1) ; symmetrieas: x = 0 ; geen nulpunten 6a Symmetrieas: x = 0 ; minimum: ( 0, ) ; nulpunten: ( 1, 0) en ( 1, 0) b Symmetrieas: x = 0 ; minimum: ( 0, ) ; nulpunten: (, 0) en (, 0) c Symmetrieas: x = 0 ; minimum: ( 0, 3) ; nulpunten: ( 1, 0) en ( 1, 0) 7a Symmetrieas: x = 0 ; maximum: ( 0, 8) ; nulpunten: (, 0) en (, 0) b Symmetrieas: x = 0 ; maximum: ( 0, 6) ; nulpunten: (, 0) en (, 0) c Symmetrieas: x = 0 ; minimum: ( 0, 7, 5) ; nulpunten: ( 1, 7, 0) en ( 1, 7, 0) d Symmetrieas: x = 0 ; minimum: ( 0, 4, 5) ; nulpunten: ( 3, 0) en ( 3, 0) ThiemeMeulenhoff 16 januari 013

45 4 Oplossen van tweedegraads vergelijkingen 1 De abc-formule Een volledige tweedegraads vergelijking heeft de vorm y = ax + bx + c. Grafieken van tweedegraads functies noemen we parabolen. We onderscheiden bergparabolen (met een maximum) en dalparabolen (met een minimum). Zie figuur 1. Figuur 1 Dalparabool, bergparabool Als voorbeeld nemen we y = x + 4x + 3. Als we de grafiek hiervan willen tekenen, is het handig om de plaats van de symmetrieas te berekenen. We kunnen dan eenvoudig de coördinaten van de top, in dit geval een minimum, berekenen. Daarnaast kunnen we het snijpunt met de y-as berekenen (vul voor x de waarde 0 in). Vervolgens berekenen we de nulpunten (snijpunten met de x-as). Ten slotte kunnen we met deze gegevens de grafiek in een assenstelsel tekenen. Om deze berekeningen te kunnen uitvoeren, gaan we uit van de algemene gedaante van een tweedegraads functie: y = ax + bx + c Voor de x-coördinaat van de top x t, tevens de plaats van de symmetrieas, geldt b de formule: xt =. De y-coördinaat van de top y t berekenen we door de eerst a berekende x t in de vergelijking in te vullen. De top is een maximum als we te maken hebben met een bergparabool, dit is het geval als a < 0. De top is een minimum bij een dalparabool, dit is het geval als a > 0. ThiemeMeulenhoff 16 januari 013

46 4 Oplossen van tweedegraads vergelijkingen Met de zogenaamde abc-formule berekenen we de nulpunten: x 1, = b ± b 4ac a De abc-formule bestaat eigenlijk uit een combinatie van twee formules: x 1 b b 4ac = a en x b + b 4ac = a Het deel b Als geldt: 4ac onder het wortelteken heet de discriminant. b 4 a c > 0, dan zijn er twee nulpunten. b 4 a c = 0, dan is er één nulpunt (eigenlijk twee samenvallende nulpunten). b 4 a c < 0, dan hebben we geen nulpunten. De abc-formule en de symmetrieas Vb. 1 Gegeven De functie f( x) = x + 4x + 3. Gevraagd Bereken de symmetrieas en het minimum of maximum. Oplossing We vergelijken de standaardvergelijking y = ax + bx + c met de functie f( x) = 1 x + 4x + 3. We zien dat a gelijk is aan het getal bij de x, dus a = 1 (we mogen x schrijven als 1 x ). Verder geldt dat b het getal is bij de x, dus b = 4. Ten slotte is c het losse getal, dus c = 3. Met a = 1, b = 4 en c = 3 gaan we onze formules invullen: b x t x 4 4 = t = = = a 1 Het is een dalparabool, want a > 0( a = 1), dus we hebben een minimum. t t t t y = x + 4x + 3 y = ( ) + 4 ( ) + 3 = = 1 Minimum: (, 1) ThiemeMeulenhoff 16 januari 013

47 Oplossen van tweedegraads vergelijkingen 43 Oefeningen 1 Bereken de symmetrieas en het minimum of maximum van: a f( x) = x + 8x + 15 b f( x) = x + x + 7 c f( x) = x 4x + 5 d f( x) = 3x + 6x + 8 Bereken de symmetrieas en het minimum of maximum van: a y = x 7x + 10 b y = x + 5x + 1 c y = 3x 7, 5x 13 d y = 10x + 10x + 9 ThiemeMeulenhoff 16 januari 013

48 44 Oplossen van tweedegraads vergelijkingen 3 De abc-formule en de nulpunten Vb. Gegeven x + 8x + 15 = 0 Gevraagd Bereken de nulpunten. Oplossing x + 8x + 15 = 0 a = 1, b = 8 en c = 10 1,, x b ± b 4ac 8 ± ± 4 8 ± 4, 9 = x1 = = = a 1 8 4, 9 1, , 9 3, 1 x 1 = = = 6, 45 of x = = = 1, 55 Nulpunten: ( 1, 55, 0 ) en ( 6, 45, 0) 3 Bereken de nulpunten van: a x 6x 6 = 0 b x 9x + 14 = 0 c x 7x + 10 = 0 d x + 10x + 1 = 0 e x 7x + 1 = 0 ThiemeMeulenhoff 16 januari 013

49 Oplossen van tweedegraads vergelijkingen 45 4 Bereken de nulpunten van: a x 6x + 9 = 0 b 9x + 6x 35 = 0 c 10x 19x + 6 = 0 d 35x 11x + 30 = 0 e x + x + 1 = 0 5 Bereken de nulpunten van: a x + 6x + 9 = 0 b x + 4x 5 = 0 c x + 8x 7 = 0 d x 3x + = 0 e x + 5x + 1 = 0 ThiemeMeulenhoff 16 januari 013

50 46 Oplossen van tweedegraads vergelijkingen 4 Het functieonderzoek en het tekenen van de grafiek Als we een volledige tweedegraads vergelijking willen onderzoeken en tekenen, moeten we de volgende vijf stappen nemen: 1. Bereken de symmetrieas.. Bereken het maximum of minimum. 3. Bereken de nulpunten. 4. Bereken het snijpunt met de y-as. 5. Verzamel de resultaten in een xy-tabel en teken van daaruit de grafiek. Vb. 3 Gegeven y = x + 4x + 3 Gevraagd a. Bereken de symmetrieas. b. Bereken het maximum of minimum. c. Bereken de nulpunten. d. Bereken het snijpunt met de y-as. e. Teken de grafiek. Oplossing a. a = 1, b = 4 en c = 3 b Symmetrieas: x = a = 4 = 4 =, x = 1 b. Het is een dalparabool t yt = xt + 4xt + 3 yt = ( ) + 4 ( ) + 3 = = 1. Minimum: (, 1) c. x b ± b 4ac 4 ± ± 4 4 ± = x1 = = = a 1 1,, x 1 = = = 3 of x = = = 1 Nulpunten: ( 3, 0) en ( 1, 0) d. Snijpunt met de y-as, dan geldt: x = 0 y = = 3 ( 0, 3). ThiemeMeulenhoff 16 januari 013

51 Oplossen van tweedegraads vergelijkingen 47 e. Zie tabel. x y = x + 4x Tabel 1 y x Figuur Vb. 4 Gegeven f( x) = x + x 3 Gevraagd a. Bereken de symmetrieas. b. Bereken het maximum of minimum. c. Bereken de nulpunten. d. Bereken het snijpunt met de y-as. e. Teken de grafiek. Oplossing a. a = 1, b = en c = 3 b Symmetrieas: x = a = = = 1, x t = 1 1 b. Het is een bergparabool yt = xt + xt 3 yt = ( 1) = =. Maximum: ( 1, ) c. b 4 a c = = 4 1 = 8, dus b 4 a c < 0. er zijn geen nulpunten. d. Snijpunt met de y-as, dan geldt: x = 0 y = ( 0) = 3 ( 0, 3). ThiemeMeulenhoff 16 januari 013

52 48 Oplossen van tweedegraads vergelijkingen e. Zie tabel. x 0 1 y = x + x Tabel y Figuur 3 x Bereken de symmetrieas, het maximum of minimum, de nulpunten, het snijpunt met de y-as en teken de grafiek van: a y = x x 3 b y = x + 3x + c y = x 4x + 1 d f( x) = x + 4x 1 ThiemeMeulenhoff 16 januari 013

53 Oplossen van tweedegraads vergelijkingen 49 7 Bereken de symmetrieas, het maximum of minimum, de nulpunten, het snijpunt met de y-as en teken de grafiek van: a f( x) = x x 6 b y = x + x + 15 ThiemeMeulenhoff 16 januari 013

54 50 Oplossen van tweedegraads vergelijkingen c y = x + 3x d f( x) = x + 6x 5 ThiemeMeulenhoff 16 januari 013

55 Oplossen van tweedegraads vergelijkingen 51 Antwoorden 1a x = 4, minimum ( 4, 1) b x = 1, maximum ( 1, 8) c x = 1, minimum ( 1, 3) d x = 1, maximum ( 1, 11) a x = 3, 5, minimum ( 3, 5,, 5) b x =, 5, maximum (, 5, 18, 5) c x = 1, 5, minimum ( 1, 5, 17, 7) d x = 0, 5, maximum ( 0, 5, 11, 5) 3a ( 6, 9, 0 ) en ( 0, 9, 0) b (, 0 ) en ( 7, 0) c (, 0 ) en ( 5, 0) d ( 7, 0 ) en ( 3, 0) e ( 3, 0 ) en ( 4, 0) 4a ( 3, 0) b (, 3, 0 ) en ( 1, 7, 0) c ( 0, 4, 0 ) en ( 1, 5, 0) d Geen nulpunten e Geen nulpunten 5a ( 1,, 0 ) en ( 7,, 0) b Geen nulpunten c ( 1, 0 ) en ( 7, 0) d ( 1, 0 ) en (, 0) e ( 0,, 0 ) en (, 7, 0) 6a Symmetrieas: x = 1. Minimum: ( 1, 4 ). Nulpunten: ( 1, 0 ) en ( 3, 0 ). Snijpunt met de y-as: ( 0, 3 ). b Symmetrieas: x = 1, 5. Minimum: ( 1, 5, 0, 5 ). Nulpunten: (, 0 ) en ( 1, 0 ). Snijpunt met de y-as: ( 0, ). c Symmetrieas: x =. Minimum: (, 3 ). Nulpunten: ( 0, 3, 0 ) en ( 3, 7, 0 ). Snijpunt met de y-as: ( 0, 1 ). d Symmetrieas: x =. Maximum: (, 3 ). Nulpunten: ( 0, 7, 0 ) en ( 3, 73, 0 ). Snijpunt met de y-as: ( 0, 1 ). 7a Symmetrieas: x = 0, 5. Minimum: ( 0, 5, 6,5). Nulpunten: (, 0 ) en ( 3, 0). Snijpunt met de y-as: ( 0, 6). b Symmetrieas: x = 1. Maximum: ( 1, 16). Nulpunten: ( 3, 0 ) en ( 5, 0). Snijpunt met de y-as: ( 0, 15). c Symmetrieas: x = 0, 75. Minimum: ( 0,75, 1, 15 ). Nulpunten: ( 1,5, 0 ) en ( 0, 0). Snijpunt met de y-as: ( 0, 0). d Symmetrieas: x = 3. Maximum: ( 3, 4). Nulpunten: ( 1, 0) en ( 5, 0). Snijpunt met de y-as: ( 0, 5). ThiemeMeulenhoff 16 januari 013

56