4. Exponentiële vergelijkingen
|
|
|
- Johanna Clara van den Broek
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 4. Exponentiële vergelijkingen Exponentiële vergelijkingen De gelijkheid 10 3 = 1000 bevat drie getallen: 10, 3 en Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen onderscheiden: 1) We weten de 1000 niet, als we op die plaats een x zetten volgt: 10 3 = x de uitkomst x = = 1000 heet de derde macht van 10. 2) We weten de 10 niet, als we op die plaats een x zetten volgt: x 3 = 1000 de uitkomst x = heet de derdemachtswortel van ) We weten de 3 niet, als we op die plaats een x zetten volgt: 10 X = 1000 de uitkomst x = 3 noemen we de 10-logaritme van We schrijven dat als x = 10 log 1000 waarbij 10 hier het grondtal van de logaritme is. Als we bijvoorbeeld de vergelijking 10 X = 23 willen oplossen weten we dat x = 10 log 23. Met de log-toets op onze rekenmachine kunnen we de 10-logaritme van een getal berekenen. Op de CASIO fx-82 typen we [log][23][=]. Het resultaat is 1,3617. Ter controle berekenen we 10 1,3617 = 22,9985. (waarom niet exact 23? ) Voorbeeld 1: 10 3 X = x = 10 log x = 2,5441 x = 2, = 0,8480. We typen in: [log][350][=][ ][3][=] 1 Los de volgende vergelijkingen op en geef de antwoorden in drijvende komma notatie a) 10 X = 35 b) 10 X = 200 c) 10 X = 3000 d) 10 3 X = 550 e) 10 5 X = 1200 f) 10 2 X = 4500 Voorbeeld 2: X = X = X = 20 4 x = 10 log 20 4 x = 1,3010 x = 1, x = 0,3253 We typen: [100][ ][5][=][log][ANS][=][ ][4][=] 2 Los de volgende vergelijkingen op en geef de antwoorden in drijvende komma notatie a) 5 10 X = 35 b) 4 10 X = 200 c) X = 3000 d) X = 55 e) X = 120 f) X = 450 blz 401
2 Logaritmen met grondtal 10 gebruiken we het meest. Daarom vermelden we bij logaritmen met grondtal 10 meestal niet meer het grondtal, dus log 5 betekent 10 log 5. Met de ln-toets op de rekenmachine kunnen we logaritmen uitrekenen met grondtal e. Het getal e is net zoals een natuurkonstante. ( e 2,71828 ) Een logaritme met grondtal e noemen we een natuurlijke logaritme en duiden we aan met ln. ln x is dus eigenlijk een andere schrijfwijze voor e log x. Als we de vergelijking e X = 23 willen oplossen weten we dat x = e log 23 = ln 23. Op de CASIO fx-82 typen we [ln][23][=]. Het resultaat is 3,1355. Ter controle berekenen we e 3,1355 = 23,0001. Voorbeeld 3: e 3 R = 24 3 R = ln 24 3 R = 3,1781 R = 3, R = 1,0594. We typen: [ln][24][=][ ][3][=] 3 Los de volgende vergelijkingen op en geef de antwoorden in drijvende komma notatie a) e X = 35 b) e X = 200 c) e X = 3000 d) e 3 X = 550 e) e 5 X = 1200 f) e 2 X = 4500 Een macht met grondtal e zoals e 5 X noemen we een e-macht. Voorbeeld 4: 3 e 2 X = 12 e 2 X = 12 3 e 2 X = 4 2 x = ln 4 2 x = 1,3863 x = 1, x = 0,6931. We typen: [12][ ][3][=][ln][ANS][=][ ][2][=] Voorbeeld 5: 6 3 e 2 X = 4-3 e 2 X = e 2 X = e 2 X = -2 e 2 X = -2-3 e 2 X = 0, x = ln 0, x = -0,4055 x = -0, x = -0, Los de volgende vergelijkingen op en geef de antwoorden in drijvende komma notatie a) 5 e -3 T = 4 b) 3 e -4 T = 5 c) 6-6 e -3 T = 2 d) 4-5 e -3 T = 2 e) 8-5 e 3 T = 4 f) 7-2 e 4 T = 3 blz 402
3 Als we de vergelijking 5 X = 30 willen oplossen weten we al dat x = 5 log 30. Het probleem is natuurlijk dat de logaritme met grondtal 5 niet op onze rekenmachine zit. We hebben wat meer kennis nodig over de eigenschappen van logaritmen. We gaan gebruik maken van de volgende formule: C log b a log b = C log a c mag een willekeurig getal zijn, we kiezen natuurlijk een grondtal dat op onze rekenmachine zit dus met c = 10 wordt onze formule: 10 log b a log b = 10 log a Dat betekent dat we 5 log 30 uit kunnen rekenen met log 30 log 5 = 2,1133. We controleren weer 5 2,1133 = 30,0008. ( weten we nog hoe we machten intypen? ) 10 X = 35 x = log 35 x = 1,5441 e X = 45 x = ln 45 x = 3,8067 Overzicht 8 X = 60 x = log 60 log 8 x = 1, Los de volgende vergelijkingen op en geef de antwoorden in drijvende komma notatie a) 3 X = 35 b) 4 X = 200 c) 5 X = 3000 d) 8 3 X = 550 e) 12 5 X = 1200 f) 34 2 X = 4500 Voorbeeld 6: we willen de vergelijking 6 3 Y 4 = 45 oplossen. Er volgt met de definitie van logaritme: 3 Y 4 = 6 log 45 3 Y 4 = log 45 log 6 3 Y 4 = 2, Y = 2, Y = 6,1245 Y = 6, Y = 2,0415. Controle: 6 3 2, = 6 2,1245 = 44, Los de volgende vergelijkingen op en geef de antwoorden in drijvende komma notatie a) 5 2 W + 4 = 63 b) 6-2 X 3 = 52 c) 14 3 Z + 4 = 148 d) 7 2 W + 4 = 155 e) 16-2 X 3 = 466 f) Z + 5 = 96 blz 403
4 We hebben nu gezien dat we logaritmen nodig hebben voor het oplossen van vergelijkingen waar de onbekende in de exponent staat. We noemen dergelijke vergelijkingen daarom exponentiële vergelijkingen 7 Los de volgende exponentiële vergelijkingen op en geef de antwoorden in wetenschappelijke notatie a) 4-7 e -3 T = 2 b) 8-5 e 3 T = 7 c) 9-2 e 4 T = 3 d) 8 3 X = 660 e) 12 5 X = 930 f) 48 2 X = 4500 g) 5 2 W + 8 = 155 h) 26-2 X 5 = 430 i) Z + 5 = 96 Voorgaande e-machten spelen een grote rol in formules voor het laden en ontladen van condensatoren via weerstanden. We bekijken het volgende voorbeeld waarbij we exponentiële vergelijkingen moeten oplossen. We laden een condensator C via een weerstand R: U in R C U uit Voor de uitgangsspanning U uit geldt de formule U uit = U in ( 1 e -t/ ). t is daarbij de tijd in sekonden en de tijdconstante van de schakeling in sekonden. De tijdconstante (Griekse t, spreek uit als touw ) berekenen we door de waarden van de weerstand en de condensator met elkaar te vermenigvuldigen dus = R C. Voorbeeld: als R = 100 k en C = 33 F geldt = = 3,3 s. De grafiek van U uit ziet er voor bijvoorbeeld U in = 10 V als volgt uit: U uit a b c 0 t Voor grafiek a geldt = 1 s, voor grafiek b geldt = 2 s en voor grafiek c geldt = 4 s. We zien dus dat hoe groter de tijdconstante is, hoe langzamer de spanning over de condensator oploopt. blz 404
5 We gaan berekenen wanneer de uitgangsspanning 5 V is bij een tijdconstante van 1 s: Voor de uitgangsspanning geldt U uit = e -t. Als U uit = 5 V moeten we de exponentiële vergelijking e -t = 5 oplossen. Er volgt: -10 e -t = e -t = -5 e -t = -5 / -10 e -t = 0,5 -t = ln 0,5 -t = -0,6931 t = 0,6931 s. Vervolgens gaan we berekenen wanneer de uitgangsspanning 5 V is bij een tijdconstante van 4 s: Voor de uitgangsspanning geldt U uit = e -t/4. Als U uit = 5 V moeten we de exponentiële vergelijking e -t/4 = 5 oplossen. Er volgt: -10 e -t/4 = e -t/4 = -5 e -t/4 = -5 / -10 e -t/4 = 0,5 -t/4 = ln 0,5 -t/4 = -0,6931 t = 4 0,6931 t = 2,7724 s. We zien duidelijk dat het bij een grotere tijdconstante langer duurt voordat de uitgangsspanning een bepaalde waarde bereikt. We krijgen een grotere tijdconstante door de R of de C een grotere waarde te geven. Behalve bij exponentiële vergelijkingen komen we logaritmen veelvuldig tegen in de techniek. We gebruiken in diagrammen een logaritmische schaal wanneer een grootheid kan variëren van heel klein tot heel groot zoals bij transistorkarakteristieken en frequentiediagrammen. In de geluidstechniek wordt de geluidsintensiteit uitgedrukt in decibel, een logaritmisch verhoudingsgetal. Dat geldt ook voor de geluidsisolatie van een wand. In de audiotechniek drukken we de versterking van een versterker vaak uit in decibel. Om het volume te regelen gebruiken we logaritmische potentiometers. In de chemie geven we de sterkte van een zuur weer door zijn zuurgraad. Deze wordt uitgedrukt in een ph-getal. Zuiver water heeft een ph-waarde van 7. Hoe lager het ph-getal, hoe zuurder de vloeistof. Ook dit ph-getal is een logaritmische waarde. In de seismologie registreren we aardbevingen met een seismograaf. Dit apparaat geeft de uitwijking door een aardbevingsgolf weer in een seismogram. De kracht van een aardbeving wordt uitgedrukt door een getal op de schaal van Richter. Bij deze schaal wordt de logaritme gebruikt van de grootste uitwijking die in het seismogram voorkomt. Om aardbevingen met elkaar te kunnen vergelijken gebruiken we seismogrammen die op een afstand van 100 km van het epicentrum zijn gemaakt. Het epicentrum is de plaats aan het oppervlak van de aarde waar de beving het eerste optreedt. blz 405
6 Antwoorden exponentiële vergelijkingen Exponentiële vergelijkingen 1 a) 1,5441 b) 2,3010 c) 3,4771 d) 0,9135 e) 0,6158 f) 1, a) 0,8451 b) 1,6990 c) 2,0000 d) 0,2330 e) 0,2602 f) 0, a) 3,5553 b) 5,2983 c) 8,0064 d) 2,1033 e) 1,4180 f) 4, a) 0,0744 b) -0,1277 c) 0,1352 d) 0,3054 e) 0,0744 f) 0, a) 3,2362 b) 3,8219 c) 4,9746 d) 1,0115 e) 0,5707 f) 1, a) 0,7129 b) 2,6026 c) 0,7021 d) 0,7041 e) 2,6080 f) 1, a) 4, b) 5, c) 2, d) 1,0407 e) 5, f) 1,0865 g) 2,4332 h) 3,4306 i) 1,0694 blz 406
4. Exponentiële vergelijkingen
 4. Exponentiële vergelijkingen De gelijkheid 10 3 = 1000 bevat drie getallen: 10, 3 en 1000. Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen onderscheiden:
4. Exponentiële vergelijkingen De gelijkheid 10 3 = 1000 bevat drie getallen: 10, 3 en 1000. Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen onderscheiden:
Exponentiële vergelijkingen en groei
 Exponentiële vergelijkingen en groei De gelijkheid 10 2 = 100 bevat drie getallen: 10, 2 en 100. Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen
Exponentiële vergelijkingen en groei De gelijkheid 10 2 = 100 bevat drie getallen: 10, 2 en 100. Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen
Toepassingen van logaritmen
 Toepassingen van logaritmen In de techniek krijgen we vaak met logaritmen te maken. We gebruiken in diagrammen een logaritmische schaal wanneer een grootheid kan variëren van heel klein tot heel groot
Toepassingen van logaritmen In de techniek krijgen we vaak met logaritmen te maken. We gebruiken in diagrammen een logaritmische schaal wanneer een grootheid kan variëren van heel klein tot heel groot
1) We weten de 100 niet, als we op die plaats een x zetten volgt: 10 2 = x de uitkomst x = 100 heet de tweede macht van 10.
 4. Geluid Wat is een logaritme? De gelijkheid 10 2 = 100 bevat drie getallen: 10, 2 en 100. Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen onderscheiden:
4. Geluid Wat is een logaritme? De gelijkheid 10 2 = 100 bevat drie getallen: 10, 2 en 100. Als we van die drie getallen er één niet weten moeten we hem kunnen berekenen. We kunnen dus drie gevallen onderscheiden:
Logaritmen. Het tijdstip t waarop S(t) = is op de t-as aangegeven. Dat tijdstip komt niet mooi uit. Dat tijdstip noemen 5,3
 5 Logaritmen 1 We bekijken de Shigella-bacterie uit opgave 1 van de vorige paragraaf. Hieronder staat een stukje van de grat fiek van de functie S(t) = 5,. Het tijdstip t waarop S(t) = 100.000 is op de
5 Logaritmen 1 We bekijken de Shigella-bacterie uit opgave 1 van de vorige paragraaf. Hieronder staat een stukje van de grat fiek van de functie S(t) = 5,. Het tijdstip t waarop S(t) = 100.000 is op de
1. Orthogonale Hyperbolen
 . Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
. Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
Analyse. Samenvatting: logaritmen. Frank Derks Gerard Heijmeriks www.demathe.nl
 Analyse Samenvatting: logaritmen Frank Derks Gerard Heijmeriks www.demathe.nl 1. Inhoudsopgave 1. Inhoudsopgave... 2 2. Exponentiële functies... 3 2.1. Inleiding... 3 2.2. Groeifactoren en groeipercentages...
Analyse Samenvatting: logaritmen Frank Derks Gerard Heijmeriks www.demathe.nl 1. Inhoudsopgave 1. Inhoudsopgave... 2 2. Exponentiële functies... 3 2.1. Inleiding... 3 2.2. Groeifactoren en groeipercentages...
De Wetenschappelijke notatie
 De Wetenschappelijke notatie Grote getallen zijn vaak lastig te lezen. Hoeveel is bijvoorbeeld 23000000000000? Eén manier om het lezen te vergemakkelijken is het zetten van puntjes of spaties: 23.000.000.000.000
De Wetenschappelijke notatie Grote getallen zijn vaak lastig te lezen. Hoeveel is bijvoorbeeld 23000000000000? Eén manier om het lezen te vergemakkelijken is het zetten van puntjes of spaties: 23.000.000.000.000
Exact periode = 1. h = 0, Js. h= 6, Js 12 * 12 = 1,4.10 2
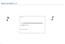 Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Paragraaf 12.1 : Exponentiële groei
 Hoofdstuk 12 Exponenten en logaritmen (V5 Wis A) Pagina 1 van 12 Paragraaf 12.1 : Exponentiële groei Les 1 Exponentiële functies Definitie Exponentiële functies Algemene formule : N = b g t waarbij b =
Hoofdstuk 12 Exponenten en logaritmen (V5 Wis A) Pagina 1 van 12 Paragraaf 12.1 : Exponentiële groei Les 1 Exponentiële functies Definitie Exponentiële functies Algemene formule : N = b g t waarbij b =
exponentiële en logaritmische functies
 CAMPUS BRUSSEL Opfriscursus Wiskunde exponentiële en logaritmische functies Exponentiële en logaritmische functies Machten van getallen 000 euro wordt belegd aan een samengestelde interest van % per jaar
CAMPUS BRUSSEL Opfriscursus Wiskunde exponentiële en logaritmische functies Exponentiële en logaritmische functies Machten van getallen 000 euro wordt belegd aan een samengestelde interest van % per jaar
exponentiële standaardfunctie
 9.0 Voorkennis In de grafiek is de eponentiële standaardfunctie f() = getekend; D f = R, B f = (0, ) met de -as als asymptoot (Dit volgt uit: lim 0 ); Elke functie g met g > heeft deze vorm; Voor g > is
9.0 Voorkennis In de grafiek is de eponentiële standaardfunctie f() = getekend; D f = R, B f = (0, ) met de -as als asymptoot (Dit volgt uit: lim 0 ); Elke functie g met g > heeft deze vorm; Voor g > is
Natuurkunde-2 GPL bakker (bk) BAKKER (2015) Algemene Technicus. Leerjaar 2. Juli 2016. K.Bakker (2015) k.bakker Technische Natuurkunde M.T.
 BAKKER (2015) Algemene Technicus Leerjaar 2 Juli 2016. K.Bakker (2015) k.bakker Technische Natuurkunde M.T.S - 1 - Inhoud Onderwerpen... 3 2. Verbanden... 4 Antwoorden verbanden... 12 3. Lineaire vergelijkingen...
BAKKER (2015) Algemene Technicus Leerjaar 2 Juli 2016. K.Bakker (2015) k.bakker Technische Natuurkunde M.T.S - 1 - Inhoud Onderwerpen... 3 2. Verbanden... 4 Antwoorden verbanden... 12 3. Lineaire vergelijkingen...
12.0 Voorkennis. Voorbeeld 1: l:y = ax + b gaat door de punten A(5, 3) en B(8, 12). Stel de functie van l op.
 12.0 Voorkennis Voorbeeld 1: l:y = ax + b gaat door de punten A(5, 3) en B(8, 12). Stel de functie van l op. Stap 1: Bepaal de richtingscoëfficiënt van l:y = ax + b : y yb ya 123 9 a 3 x x x 8 5 3 Hieruit
12.0 Voorkennis Voorbeeld 1: l:y = ax + b gaat door de punten A(5, 3) en B(8, 12). Stel de functie van l op. Stap 1: Bepaal de richtingscoëfficiënt van l:y = ax + b : y yb ya 123 9 a 3 x x x 8 5 3 Hieruit
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/98/138669860.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
logaritmen WISNET-HBO update jan Zorg dat je het lijstje met rekenregels hebt klaarliggen als je met deze training begint.
 Training Vergelijkingen met logaritmen WISNET-HBO update jan. 0 Inleiding Voor deze training heb je nodig: de rekenregels van machten de rekenregels van de logaritmen Zorg dat je het lijstje met rekenregels
Training Vergelijkingen met logaritmen WISNET-HBO update jan. 0 Inleiding Voor deze training heb je nodig: de rekenregels van machten de rekenregels van de logaritmen Zorg dat je het lijstje met rekenregels
Die moeilijke decibels.
 Die moeilijke decibels. Hoe werkt het en hoe moet ik er mee rekenen? PA FWN Met potlood en papier Er wordt zoveel mogelijk een rekenmethode toegepast, welke door zijn eenvoud met een simpele rekenmachine
Die moeilijke decibels. Hoe werkt het en hoe moet ik er mee rekenen? PA FWN Met potlood en papier Er wordt zoveel mogelijk een rekenmethode toegepast, welke door zijn eenvoud met een simpele rekenmachine
EXACT- Periode 1. Hoofdstuk Grootheden. 1.2 Eenheden.
 EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
Trillingen en geluid wiskundig
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: Logaritmen en getal e 1/3/2017. dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: Logaritmen en getal e 1/3/2017 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating) 1. Inleiding
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: Logaritmen en getal e 1/3/2017 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating) 1. Inleiding
Paragraaf 9.1 : Logaritmen
 Hoofdstuk 9 Eonentiële en Logaritmische functies (V5 Wis B) Pagina van 5 Paragraaf 9. : Logaritmen Les Logaritmen Definitie Logaritmen Hoofdregel : g t = b t = g log b met domein b>0 Om logaritmen uit
Hoofdstuk 9 Eonentiële en Logaritmische functies (V5 Wis B) Pagina van 5 Paragraaf 9. : Logaritmen Les Logaritmen Definitie Logaritmen Hoofdregel : g t = b t = g log b met domein b>0 Om logaritmen uit
Trillingen en geluid wiskundig. 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude 1 De sinus van een hoek Eenheidscirkel In de figuur hiernaast
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude 1 De sinus van een hoek Eenheidscirkel In de figuur hiernaast
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: Logaritmen en getal e. 23 juli 2015. dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Wiskunde: Logaritmen en getal e 23 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Voorbereiding toelatingsexamen arts/tandarts Wiskunde: Logaritmen en getal e 23 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Cijfer = totaal punten/10 met minimum 1
 VOORBLAD SCHRIFTELIJKE TOETSEN OPLEIDING TOETSCODE GROEP Me MeWIS1-T1 MeP1 TOETSDATUM 7 november 011 TIJD 13.00 14.30 uur AANTAL PAGINA S (incl. dit voorblad) 6 DEZE TOETS BESTAAT UIT (aantal) GEBRUIK
VOORBLAD SCHRIFTELIJKE TOETSEN OPLEIDING TOETSCODE GROEP Me MeWIS1-T1 MeP1 TOETSDATUM 7 november 011 TIJD 13.00 14.30 uur AANTAL PAGINA S (incl. dit voorblad) 6 DEZE TOETS BESTAAT UIT (aantal) GEBRUIK
Rekenkunde, eenheden en formules voor HAREC. 10 april 2015 presentator : ON5PDV, Paul
 Rekenkunde, eenheden en formules voor HAREC 10 april 2015 presentator : ON5PDV, Paul Vooraf : expectation management 1. Verwachtingen van deze presentatie (inhoud, diepgang) U = R= R. I = 8 Ω. 0,5 A =
Rekenkunde, eenheden en formules voor HAREC 10 april 2015 presentator : ON5PDV, Paul Vooraf : expectation management 1. Verwachtingen van deze presentatie (inhoud, diepgang) U = R= R. I = 8 Ω. 0,5 A =
Logaritmische functie
 Logaritmische functie WISNET-HBO update aug 2013 1 Inleiding De bedoeling van deze les is het repeteren met pen en papier van logaritmen. Voorkennis van de rekenregels van machten is voor deze les beslist
Logaritmische functie WISNET-HBO update aug 2013 1 Inleiding De bedoeling van deze les is het repeteren met pen en papier van logaritmen. Voorkennis van de rekenregels van machten is voor deze les beslist
Werken met machten en logaritmen
 1 Werken met machten en logaritmen Je mag ook werken met de formules RATE en NPER (of je gebruikt de Solver). Je moet het gevonden resultaat steeds kunnen bespreken. Basisformule samengestelde intrest
1 Werken met machten en logaritmen Je mag ook werken met de formules RATE en NPER (of je gebruikt de Solver). Je moet het gevonden resultaat steeds kunnen bespreken. Basisformule samengestelde intrest
Paragraaf 5.1 : Machten en wortels
 Hoofdstuk 5 Machten, exponenten en logaritmen (H Wis B) Pagina 1 van 1 Paragraaf 5.1 : Machten en wortels Machtsregels SPECIAAL GEVAL MACHTREGEL 1 : MACHTREGEL 2 : MACHTREGEL : a p a q = a p+q a p aq =
Hoofdstuk 5 Machten, exponenten en logaritmen (H Wis B) Pagina 1 van 1 Paragraaf 5.1 : Machten en wortels Machtsregels SPECIAAL GEVAL MACHTREGEL 1 : MACHTREGEL 2 : MACHTREGEL : a p a q = a p+q a p aq =
Inleiding goniometrie
 Inleiding goniometrie We bekijken de volgende twee hellingen: 1 2 Duidelijk is dat de tweede helling steiler is dan de eerste helling. Ook zien we dat hellingshoek 2 groter is dan hellingshoek 1. Er bestaat
Inleiding goniometrie We bekijken de volgende twee hellingen: 1 2 Duidelijk is dat de tweede helling steiler is dan de eerste helling. Ook zien we dat hellingshoek 2 groter is dan hellingshoek 1. Er bestaat
Hoofdstuk 5: TABELLEN
 Hoofdstuk 5: TABELLEN 1. Wat moet ik leren? (handboek p. 172-201 5.1 Tabellen en staafdiagrammen 1 / 6 H4 Tabellen, staafdiagrammen en grafieken 5.2 Grafieken lezen Een grafiek en een staafdiagram herkennen.
Hoofdstuk 5: TABELLEN 1. Wat moet ik leren? (handboek p. 172-201 5.1 Tabellen en staafdiagrammen 1 / 6 H4 Tabellen, staafdiagrammen en grafieken 5.2 Grafieken lezen Een grafiek en een staafdiagram herkennen.
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/31/15201373.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
9.1 Logaritmische en exponentiële vergelijkingen [1]
![9.1 Logaritmische en exponentiële vergelijkingen [1] 9.1 Logaritmische en exponentiële vergelijkingen [1]](/thumbs/71/65170233.jpg) 9.1 Logaritmische en eonentiële vergelijkingen [1] Voor logaritmen gelden de volgende rekenregels: (1) log( ab) log( a) log( b) g g g () g g g (4) (3) g n g (5) g log() = y volgt = g y Voorbeeld: a log
9.1 Logaritmische en eonentiële vergelijkingen [1] Voor logaritmen gelden de volgende rekenregels: (1) log( ab) log( a) log( b) g g g () g g g (4) (3) g n g (5) g log() = y volgt = g y Voorbeeld: a log
Noorderpoortcollege School voor MBO Stadskanaal. Reader. Reader Wiskunde MBO Niveau 4 Periode. M. van der Pijl. Transfer Database
 Noorderpoortcollege School voor MBO Stadskanaal Reader Reader Wiskunde MBO Niveau Periode M. van der Pijl Transfer Database ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet
Noorderpoortcollege School voor MBO Stadskanaal Reader Reader Wiskunde MBO Niveau Periode M. van der Pijl Transfer Database ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet
3. Lineaire vergelijkingen
 3. Lineaire vergelijkingen Lineaire vergelijkingen De vergelijking 2x = 3 noemen we een eerstegraads- of lineaire vergelijking. De onbekende x komt er namelijk tot de eerste macht in voor. Een eerstegraads
3. Lineaire vergelijkingen Lineaire vergelijkingen De vergelijking 2x = 3 noemen we een eerstegraads- of lineaire vergelijking. De onbekende x komt er namelijk tot de eerste macht in voor. Een eerstegraads
Grofweg zijn er twee typen redeneervraagstukken. A. Gedrag van een formule verklaren. B. Het doorzien van de structuur van de formule.
 Redeneren met formules Redeneren met formules is een regelmatig terugkerend onderwerp op examens. Kijk maar eens als extreem voorbeeld naar de opgave Behendigheid uit het examen VWO wiskunde 2012 tijdvak
Redeneren met formules Redeneren met formules is een regelmatig terugkerend onderwerp op examens. Kijk maar eens als extreem voorbeeld naar de opgave Behendigheid uit het examen VWO wiskunde 2012 tijdvak
(ont)wikkelen. Aantal keer gevouwen Aantal lagen papier
 (ont)wikkelen versie 0.5 [4--008] pagina (ont)wikkelen vouwen Wist je dat je een blad papier niet meer dan zeven (misschien acht) keer kunt dubbelvouwen? Om dit te controleren kun je met een stuk papier
(ont)wikkelen versie 0.5 [4--008] pagina (ont)wikkelen vouwen Wist je dat je een blad papier niet meer dan zeven (misschien acht) keer kunt dubbelvouwen? Om dit te controleren kun je met een stuk papier
DE DECIBEL. a logb = x => a x = b en a alogb = b of. \ 1, b R 0
 DE DECIBEL 1. Inleiding De decibel is één van de meest gebruikte functionele eenheid die toegepast wordt in elektronica, audio, akoustiek en antennetechnieken (antennes, versterkers en lange lijnen). De
DE DECIBEL 1. Inleiding De decibel is één van de meest gebruikte functionele eenheid die toegepast wordt in elektronica, audio, akoustiek en antennetechnieken (antennes, versterkers en lange lijnen). De
8 Oefeningen bij dehoofdstukken 5, 6 en 7 van deel Logaritmen met andere grondtallen dan Overzicht en oefening bij logaritmen 10
 deel 2 Inhoudsopgave 8 Oefeningen bij dehoofdstukken 5, 6 en 7 van deel 1 3 9 Logaritmen met andere grondtallen dan 10 6 10 Overzicht en oefening bij logaritmen 10 Dit is een vervolg op Verbanden, Exponenten
deel 2 Inhoudsopgave 8 Oefeningen bij dehoofdstukken 5, 6 en 7 van deel 1 3 9 Logaritmen met andere grondtallen dan 10 6 10 Overzicht en oefening bij logaritmen 10 Dit is een vervolg op Verbanden, Exponenten
REKENTECHNIEKEN - OPLOSSINGEN
 REKENTECHNIEKEN - OPLOSSINGEN 1] 3,52 m + 13,6 cm =? 3,52 m 3,52 m - 2 13,6 cm 0,136 m - 3 3,656 m eindresultaat 3,66 m 2 cijfers na komma en afronden naar boven 3,52 m 352 cm - 0 13,6 cm 13,6 cm - 1 365,6
REKENTECHNIEKEN - OPLOSSINGEN 1] 3,52 m + 13,6 cm =? 3,52 m 3,52 m - 2 13,6 cm 0,136 m - 3 3,656 m eindresultaat 3,66 m 2 cijfers na komma en afronden naar boven 3,52 m 352 cm - 0 13,6 cm 13,6 cm - 1 365,6
Wiskunde voor bachelor en master Deel 1 Basiskennis en basisvaardigheden. c 2015, Syntax Media, Utrecht Uitwerkingen hoofdstuk 11
 Wiskunde voor bachelor en master Deel Basiskennis en basisvaardigheden c 05, Syntax Media, Utrecht www.syntaxmedia.nl Uitwerkingen hoofdstuk.. a. In de onderstaande figuur zijn de grafieken van y = ( )x,
Wiskunde voor bachelor en master Deel Basiskennis en basisvaardigheden c 05, Syntax Media, Utrecht www.syntaxmedia.nl Uitwerkingen hoofdstuk.. a. In de onderstaande figuur zijn de grafieken van y = ( )x,
1 Rekenen met gehele getallen
 1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
Transformaties van grafieken HAVO wiskunde B deel 1
 Transformaties van grafieken HAVO wiskunde B deel Willem van Ravenstein 500765005 Haags Montessori Lyceum (c) 06 Inleiding In de leerroute transformaties van grafieken gaat het om de karakteristieke eigenschappen
Transformaties van grafieken HAVO wiskunde B deel Willem van Ravenstein 500765005 Haags Montessori Lyceum (c) 06 Inleiding In de leerroute transformaties van grafieken gaat het om de karakteristieke eigenschappen
3.0 Voorkennis. y = -4x + 8 is de vergelijking van een lijn. Hier wordt y uitgedrukt in x.
 3.0 Voorkennis y = -4x + 8 is de vergelijking van een lijn. Hier wordt y uitgedrukt in x. y = -4x + 8 kan herschreven worden als y + 4x = 8 Dit is een lineaire vergelijking met twee variabelen. Als je
3.0 Voorkennis y = -4x + 8 is de vergelijking van een lijn. Hier wordt y uitgedrukt in x. y = -4x + 8 kan herschreven worden als y + 4x = 8 Dit is een lineaire vergelijking met twee variabelen. Als je
De uitleg in dit moduul is gebaseerd op een CASIO rekenmachine fx-82ms. Voor de verschillen met de TI-30X II zie de bijlage achterin.
 Rekenmachine 1. Rekenmachine De uitleg in dit moduul is gebaseerd op een CASIO rekenmachine fx-82ms. Voor de verschillen met de TI-30X II zie de bijlage achterin. Onze rekenmachine geeft het resultaat
Rekenmachine 1. Rekenmachine De uitleg in dit moduul is gebaseerd op een CASIO rekenmachine fx-82ms. Voor de verschillen met de TI-30X II zie de bijlage achterin. Onze rekenmachine geeft het resultaat
Meergraadsvergelijkingen
 Meergraadsvergelijkingen Meergraads vergelijkingen In dit hoofdstuk gaan we ons bezig houden met tweede- en hogeregraads vergelijkingen. In een tweedegraads vergelijking komt de onbekende x tot de tweede
Meergraadsvergelijkingen Meergraads vergelijkingen In dit hoofdstuk gaan we ons bezig houden met tweede- en hogeregraads vergelijkingen. In een tweedegraads vergelijking komt de onbekende x tot de tweede
Paragraaf 13.0 : Limieten en absolute waarde
 Hoofdstuk 13 Limieten en Asymptoten (V6 Wis B) Pagina 1 van 13 Paragraaf 13.0 : Limieten en absolute waarde Definitie absoluuttekens pp = { p absoluut of de absolute waarde van p } pp = { altijd positief
Hoofdstuk 13 Limieten en Asymptoten (V6 Wis B) Pagina 1 van 13 Paragraaf 13.0 : Limieten en absolute waarde Definitie absoluuttekens pp = { p absoluut of de absolute waarde van p } pp = { altijd positief
Schooljaar: Leerkracht: M. Smet Leervak: Wiskunde Leerplan: D/2002/0279/048
 Blz: 1/5 04 09 09 1.1 STELLING VAN PYTHAGORAS ouwregel tot Pythagoras: formulering. 07 09 09 11 09 09 14 09 09 18 09 09 21 09 09 22 09 09 25 09 09 29 09 09 01 10 09 02 10 09 06 10 09 08 10 09 09 10 09
Blz: 1/5 04 09 09 1.1 STELLING VAN PYTHAGORAS ouwregel tot Pythagoras: formulering. 07 09 09 11 09 09 14 09 09 18 09 09 21 09 09 22 09 09 25 09 09 29 09 09 01 10 09 02 10 09 06 10 09 08 10 09 09 10 09
Werken met de rekenmachine
 Werken met de rekenmachine De uitleg in dit moduul is gebaseerd op een CASIO rekenmachine van de nieuwe generatie met een twee-regelig display zoals de fx-82tl of de afgebeelde fx-82ms. Onze rekenmachine
Werken met de rekenmachine De uitleg in dit moduul is gebaseerd op een CASIO rekenmachine van de nieuwe generatie met een twee-regelig display zoals de fx-82tl of de afgebeelde fx-82ms. Onze rekenmachine
exponentiële verbanden
 exponentiële verbanden . voorkennis Procenten en vermenigvuldigingsfactoren Procentuele toename met p%: g = + p 00 p = ( g ) 00 Procentuele afname met p%: g = p 00 p = ( g) 00 De constante factor In 859
exponentiële verbanden . voorkennis Procenten en vermenigvuldigingsfactoren Procentuele toename met p%: g = + p 00 p = ( g ) 00 Procentuele afname met p%: g = p 00 p = ( g) 00 De constante factor In 859
fx-82es (PLUS) Werken met de CASIO fx-82es (PLUS) instellingen
 Werken met de CASIO fx-82es (PLUS) Deze 'gewone' rekenmachine heeft een natural display. Het intypen en aflezen van bijv breuken, machten, wortels en logaritmen gaat (eindelijk!) op een manier die logisch
Werken met de CASIO fx-82es (PLUS) Deze 'gewone' rekenmachine heeft een natural display. Het intypen en aflezen van bijv breuken, machten, wortels en logaritmen gaat (eindelijk!) op een manier die logisch
Decimaliseren. 1.1 Vereenvoudigen 2. 1.2 Verhoudingen omzetten 3. 1.3 Afronden 4. 1.4 Oefeningen 4
 Decimaliseren Samenvatting Decimaliseren is nodig, omdat alle apparaten voor hun instelling een decimaal getal nodig hebben. Bijvoorbeeld: een infuuspomp kan wel op 0,8 ml/min ingesteld worden, maar niet
Decimaliseren Samenvatting Decimaliseren is nodig, omdat alle apparaten voor hun instelling een decimaal getal nodig hebben. Bijvoorbeeld: een infuuspomp kan wel op 0,8 ml/min ingesteld worden, maar niet
Machten, exponenten en logaritmen
 Machten, eponenten en logaritmen Machten, eponenten en logaritmen Macht, eponent en grondtal Eponenten en logaritmen hebben alles met machtsverheffen te maken. Een macht als 4 is niets anders dan de herhaalde
Machten, eponenten en logaritmen Machten, eponenten en logaritmen Macht, eponent en grondtal Eponenten en logaritmen hebben alles met machtsverheffen te maken. Een macht als 4 is niets anders dan de herhaalde
14.1 Vergelijkingen en herleidingen [1]
![14.1 Vergelijkingen en herleidingen [1] 14.1 Vergelijkingen en herleidingen [1]](/thumbs/27/12007257.jpg) 4. Vergelijkingen en herleidingen [] Er zijn vier soorten bijzondere vergelijkingen: : AB = 0 => A = 0 of B = 0 ( - 5)( + 7) = 0-5 = 0 of + 7 = 0 = 5 of = -7 : A = B geeft A = B of A = - B ( ) = 5 ( )
4. Vergelijkingen en herleidingen [] Er zijn vier soorten bijzondere vergelijkingen: : AB = 0 => A = 0 of B = 0 ( - 5)( + 7) = 0-5 = 0 of + 7 = 0 = 5 of = -7 : A = B geeft A = B of A = - B ( ) = 5 ( )
LESFICHE 1. Handig rekenen. Lesfiche 1. 1 Procent & promille. 2 Afronden. Procent of percent (%) betekent letterlijk per honderd.
 Lesfiche 1 1 Procent & promille Handig rekenen Procent of percent (%) betekent letterlijk per honderd. 5 5 % is dus 5 per honderd. In breukvorm wordt dat of 0,05 als decimaal getal. Promille ( ) betekent
Lesfiche 1 1 Procent & promille Handig rekenen Procent of percent (%) betekent letterlijk per honderd. 5 5 % is dus 5 per honderd. In breukvorm wordt dat of 0,05 als decimaal getal. Promille ( ) betekent
rekenregels voor machten en logaritmen wortels waar of niet waar
 Hoofdstuk 5 - machten, eponenten en logaritmen rekenregels voor machten en logaritmen wortels waar of niet waar 0. voorkennis HERLEIDEN VAN MACHTEN - rekenregels voor machten Bij het vermenigvuldigen van
Hoofdstuk 5 - machten, eponenten en logaritmen rekenregels voor machten en logaritmen wortels waar of niet waar 0. voorkennis HERLEIDEN VAN MACHTEN - rekenregels voor machten Bij het vermenigvuldigen van
Theorie: Het maken van een verslag (Herhaling klas 2)
 Theorie: Het maken van een verslag (Herhaling klas 2) Onderdelen Een verslag van een experiment bestaat uit vier onderdelen: - inleiding: De inleiding is het administratieve deel van je verslag. De onderzoeksvraag
Theorie: Het maken van een verslag (Herhaling klas 2) Onderdelen Een verslag van een experiment bestaat uit vier onderdelen: - inleiding: De inleiding is het administratieve deel van je verslag. De onderzoeksvraag
Wiskunde 20 maart 2014 versie 1-1 -
 Wiskunde 0 maart 04 versie - -. a 3 a =. a.. 6.,AppB./ a 4 3. a 3. Rekenregels voor machten: als je twee machten op elkaar deelt, trek je de exponenten van elkaar af. De exponent van a wordt dan =. 3 6
Wiskunde 0 maart 04 versie - -. a 3 a =. a.. 6.,AppB./ a 4 3. a 3. Rekenregels voor machten: als je twee machten op elkaar deelt, trek je de exponenten van elkaar af. De exponent van a wordt dan =. 3 6
Standaardafgeleiden. Wisnet-HBO. update maart 2011
 Standaardafgeleiden Wisnet-HBO update maart 2011 1 Inleiding Als je nog niets over differentiëren weet, kun je beter eerst naar de les Wat is Differentiëren gaan in Wisnet Verder zijn er Maplets om de
Standaardafgeleiden Wisnet-HBO update maart 2011 1 Inleiding Als je nog niets over differentiëren weet, kun je beter eerst naar de les Wat is Differentiëren gaan in Wisnet Verder zijn er Maplets om de
De transferfunctie of de versterkingsfactor van een schakeling is gelijk aan de verhouding van de uitgangsspanning op de ingangsspanning.
 NETWEKEN. FITETECHNIEK.. Soorten Filters aagdoorlaatfilters Hoogdoorlaatfilters Banddoolaatfilters Bandsperfilters Wienbrug filter Alle filters kunnen zowel worden uitgevoerd met weerstanden en condensatoren
NETWEKEN. FITETECHNIEK.. Soorten Filters aagdoorlaatfilters Hoogdoorlaatfilters Banddoolaatfilters Bandsperfilters Wienbrug filter Alle filters kunnen zowel worden uitgevoerd met weerstanden en condensatoren
Antwoorden Verbanden hfd 1 t/m 7 vwo4a
 Antwoorden Verbanden hfd t/m 7 vwoa Hoofdstuk : Vouwen en rekenen met machten van Opgave a) Verdubbel telkens de vorige waarde. Bijv. na keer vouwen is het aantal lagen papier een verdubbeling van de lagen
Antwoorden Verbanden hfd t/m 7 vwoa Hoofdstuk : Vouwen en rekenen met machten van Opgave a) Verdubbel telkens de vorige waarde. Bijv. na keer vouwen is het aantal lagen papier een verdubbeling van de lagen
Noorderpoortcollege school voor MBO Stadskanaal. Reader. Wiskunde MBO Niveau 4 periode 3. M. van der Pijl. Transfer Database
 Noorderpoortcollege school voor MBO Stadskanaal Reader Wiskunde MBO Niveau 4 periode 3 M. van der Pijl Transfer Database ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet
Noorderpoortcollege school voor MBO Stadskanaal Reader Wiskunde MBO Niveau 4 periode 3 M. van der Pijl Transfer Database ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet
Wiskundige vaardigheden
 Inleiding Bij het vak natuurkunde ga je veel rekenstappen zetten. Het is noodzakelijk dat je deze rekenstappen goed en snel kunt uitvoeren. In deze presentatie behandelen we de belangrijkste wiskundige
Inleiding Bij het vak natuurkunde ga je veel rekenstappen zetten. Het is noodzakelijk dat je deze rekenstappen goed en snel kunt uitvoeren. In deze presentatie behandelen we de belangrijkste wiskundige
1.1.2. Wiskundige taal. Symbolen om mee te rekenen + optelling - aftrekking. vermenigvuldiging : deling
 Examen Wiskunde: Hoofdstuk 1: Reële getallen: 1.1 Rationale getallen: 1.1.1 Soorten getallen. Een natuurlijk getal is het resultaat van een tellg van een edig aantal dgen. Een geheel getal is het verschil
Examen Wiskunde: Hoofdstuk 1: Reële getallen: 1.1 Rationale getallen: 1.1.1 Soorten getallen. Een natuurlijk getal is het resultaat van een tellg van een edig aantal dgen. Een geheel getal is het verschil
Examencursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO kan niet korter
 Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
14.0 Voorkennis. De hierboven getekende functie herhaalt zich om de 6 seconden. Dit noemen we dan ook een periodieke functie.
 14.0 Voorkennis De hierboven getekende functie herhaalt zich om de 6 seconden. Dit noemen we dan ook een periodieke functie. Evenwichtsstand = (min + max)/2 = (-100 + 300)/2 = 100 Amplitude = max evenw.
14.0 Voorkennis De hierboven getekende functie herhaalt zich om de 6 seconden. Dit noemen we dan ook een periodieke functie. Evenwichtsstand = (min + max)/2 = (-100 + 300)/2 = 100 Amplitude = max evenw.
Technische Universiteit
 SBD 9756a 98-0-28, niv 5 A/B REKENTECHNIEKEN Technische Universiteit Eindhoven Centrum Stralingsbescherming en Dosimetrie Stralingsbeschermingsdienst Inleiding Voor het uitvoeren van berekeningen in het
SBD 9756a 98-0-28, niv 5 A/B REKENTECHNIEKEN Technische Universiteit Eindhoven Centrum Stralingsbescherming en Dosimetrie Stralingsbeschermingsdienst Inleiding Voor het uitvoeren van berekeningen in het
Kerstvakantiecursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO kan niet korter
 Voorbereidende opgaven VWO Kerstvakantiecursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk
Voorbereidende opgaven VWO Kerstvakantiecursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk
Stoomcursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO ( ) = = ( ) ( ) ( ) = ( ) ( ) = ( ) = = ( )
 Voorbereidende opgaven VWO Stoomcursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Stoomcursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
3.1 Haakjes wegwerken [1]
![3.1 Haakjes wegwerken [1] 3.1 Haakjes wegwerken [1]](/thumbs/53/31611347.jpg) 3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
Deze stelling zegt dat je iedere rechthoekige driehoek kunt maken door drie vierkanten met de hoeken tegen elkaar aan te leggen.
 Meetkunde Inleiding We beginnen met het doorlezen van alle theorie uit hoofdstuk 3 van het boek. Daar staan een aantal algemene regels goed uitgelegd. Waar je nog wat extra uitleg over nodig hebt, is de
Meetkunde Inleiding We beginnen met het doorlezen van alle theorie uit hoofdstuk 3 van het boek. Daar staan een aantal algemene regels goed uitgelegd. Waar je nog wat extra uitleg over nodig hebt, is de
Rekenmachine. Willem-Jan van der Zanden
 Rekenmachine Vanaf hoofdstuk 5 mag je bij wiskunde bij bepaalde hoofdstukken een eenvoudige rekenmachine gebruiken; Als je nog geen rekenmachine hebt, koop dan een CASIO fx; Heb je al een rekenmachine
Rekenmachine Vanaf hoofdstuk 5 mag je bij wiskunde bij bepaalde hoofdstukken een eenvoudige rekenmachine gebruiken; Als je nog geen rekenmachine hebt, koop dan een CASIO fx; Heb je al een rekenmachine
Hoofdstuk 1: Basisvaardigheden
 Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
11.0 Voorkennis. Optellen alleen bij gelijknamige termen: 3a 3 + 4a 3 = 7a 3. Bij macht van een macht exponenten vermenigvuldigen: (a 5 ) 4 = a 20
 .0 Voorkennis Herhaling rekenregels voor machten: Vermenigvuldigen is exponenten optellen: a 3 a 5 = a 8 Optellen alleen bij gelijknamige termen: 3a 3 + a 3 = 7a 3 Bij macht van een macht exponenten vermenigvuldigen:
.0 Voorkennis Herhaling rekenregels voor machten: Vermenigvuldigen is exponenten optellen: a 3 a 5 = a 8 Optellen alleen bij gelijknamige termen: 3a 3 + a 3 = 7a 3 Bij macht van een macht exponenten vermenigvuldigen:
Inhoud college 5 Basiswiskunde Taylorpolynomen
 Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Paragraaf 8.1 : Recursieve en directe formule
 Hoofdstuk 8 Rijen en veranderingen (V5 Wis A) Pagina 1 van 11 Paragraaf 8.1 : Recursieve en directe formule Les 1 Rijen en recursievergelijking Definities : Wat is een rij Gegeven is de rij u = { 5,10,20,40
Hoofdstuk 8 Rijen en veranderingen (V5 Wis A) Pagina 1 van 11 Paragraaf 8.1 : Recursieve en directe formule Les 1 Rijen en recursievergelijking Definities : Wat is een rij Gegeven is de rij u = { 5,10,20,40
(g 0 en n een heel getal) Voor het rekenen met machten geldt ook - (p q) a = p a q a
 Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
2 n 1. OPGAVEN 1 Hoeveel cijfers heeft het grootste bekende Mersenne-priemgetal? Met dit getal vult men 320 krantenpagina s.
 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Paragraaf 13.1 : Berekeningen met de afgeleide
 Hoofdstuk 13 Toepassingen vd differentiaalrekening (V5 Wis A) Pagina 1 van 7 Paragraaf 13.1 : Berekeningen met de afgeleide Differentiëren van e-machten en logaritmen f() = e f () = e f() = ln() f () =
Hoofdstuk 13 Toepassingen vd differentiaalrekening (V5 Wis A) Pagina 1 van 7 Paragraaf 13.1 : Berekeningen met de afgeleide Differentiëren van e-machten en logaritmen f() = e f () = e f() = ln() f () =
wiskunde C pilot vwo 2015-I
 Succesvogels en pechvogels In 2010 heeft Chris van Turnhout onderzoek gedaan naar de ontwikkeling van de aantallen broedvogels in Nederland gedurende de periode 1990 2005. Hij onderzocht welke eigenschappen
Succesvogels en pechvogels In 2010 heeft Chris van Turnhout onderzoek gedaan naar de ontwikkeling van de aantallen broedvogels in Nederland gedurende de periode 1990 2005. Hij onderzocht welke eigenschappen
6.0 Voorkennis AD BC. Kruislings vermenigvuldigen: Voorbeeld: 50 10x. 50 10( x 1) Willem-Jan van der Zanden
 6.0 Voorkennis Kruislings vermenigvuldigen: A C AD BC B D Voorbeeld: 50 0 x 50 0( x ) 50 0x 0 0x 60 x 6 6.0 Voorkennis Herhaling van rekenregels voor machten: p p q pq a pq a a a [] a [2] q a q p pq p
6.0 Voorkennis Kruislings vermenigvuldigen: A C AD BC B D Voorbeeld: 50 0 x 50 0( x ) 50 0x 0 0x 60 x 6 6.0 Voorkennis Herhaling van rekenregels voor machten: p p q pq a pq a a a [] a [2] q a q p pq p
Logaritmische verbanden
 9 Zes momentopnamen van een zeester Van elke zeester is de armlengte gemeten, vanuit het midden van de ster. De resultaten staat in de tabel: a. Voer de gegevens in op de GR. Dat gaat dat als volgt: Toets
9 Zes momentopnamen van een zeester Van elke zeester is de armlengte gemeten, vanuit het midden van de ster. De resultaten staat in de tabel: a. Voer de gegevens in op de GR. Dat gaat dat als volgt: Toets
5 Water, het begrip ph
 5 Water, het begrip ph 5.1 Water Waterstofchloride is een sterk zuur, het reageert als volgt met water: HCI(g) + H 2 0(I) Cl (aq) + H 3 O + (aq) z b Hierbij reageert water als base. Ammoniak is een zwakke
5 Water, het begrip ph 5.1 Water Waterstofchloride is een sterk zuur, het reageert als volgt met water: HCI(g) + H 2 0(I) Cl (aq) + H 3 O + (aq) z b Hierbij reageert water als base. Ammoniak is een zwakke
M V. Inleiding opdrachten. Opgave 1. Meetinstrumenten en grootheden. Vul het schema in. stopwatch. liniaal. thermometer. spanning.
 Inleiding opdrachten Opgave 1. Meetinstrumenten en grootheden Vul het schema in. Meetinstrument Grootheid stopwatch liniaal thermometer spanning hoek van inval oppervlak Opgave. Formules Leg de betekenis
Inleiding opdrachten Opgave 1. Meetinstrumenten en grootheden Vul het schema in. Meetinstrument Grootheid stopwatch liniaal thermometer spanning hoek van inval oppervlak Opgave. Formules Leg de betekenis
Getallenleer Inleiding op codeertheorie. Cursus voor de vrije ruimte
 Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
VAARDIGHEDEN EXCEL. MEETWAARDEN INVULLEN In de figuur hieronder zie je twee keer de ingevoerde meetwaarden, eerst ruw en daarna netjes opgemaakt.
 VAARDIGHEDEN EXCEL Excel is een programma met veel mogelijkheden om meetresultaten te verwerken, maar het was oorspronkelijk een programma voor boekhouders. Dat betekent dat we ons soms in bochten moeten
VAARDIGHEDEN EXCEL Excel is een programma met veel mogelijkheden om meetresultaten te verwerken, maar het was oorspronkelijk een programma voor boekhouders. Dat betekent dat we ons soms in bochten moeten
SAMENVATTING BASIS & KADER
 SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
Meetfouten, afronding, voorvoegsels en eenheden
 Meetfouten, afronding, voorvoegsels en eenheden Meetfouten In de wiskunde werken we meestal met exacte getallen: 2π, 5, 3, 2 log 3. Ook in natuurwetenschappelijke vakken komen exacte getallen voor, maar
Meetfouten, afronding, voorvoegsels en eenheden Meetfouten In de wiskunde werken we meestal met exacte getallen: 2π, 5, 3, 2 log 3. Ook in natuurwetenschappelijke vakken komen exacte getallen voor, maar
Noorderpoortcollege School voor MBO Stadskanaal. Reader. Wiskunde MBO Niveau 4 Periode 2. M. van der Pijl. Transfer Database
 Noorderpoortcollege School voor MBO Stadskanaal Reader Wiskunde MBO Niveau Periode M. van der Pijl Transfer Database ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet
Noorderpoortcollege School voor MBO Stadskanaal Reader Wiskunde MBO Niveau Periode M. van der Pijl Transfer Database ThiemeMeulenhoff ontwikkelt leermiddelen voor Primair Onderwijs, Algemeen Voortgezet
Achter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen.
 Examen VWO 2015 tijdvak 1 woensdag 13 mei 13.30-16.30 uur wiskunde C (pilot) Bij dit examen hoort een uitwerkbijlage. Achter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen.
Examen VWO 2015 tijdvak 1 woensdag 13 mei 13.30-16.30 uur wiskunde C (pilot) Bij dit examen hoort een uitwerkbijlage. Achter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen.
1.1 Tweedegraadsvergelijkingen [1]
![1.1 Tweedegraadsvergelijkingen [1] 1.1 Tweedegraadsvergelijkingen [1]](/thumbs/58/42425907.jpg) 1.1 Tweedegraadsvergelijkingen [1] Er zijn vier soorten tweedegraadsvergelijkingen: 1. ax 2 + bx = 0 (Haal de x buiten de haakjes) Voorbeeld 1: 3x 2 + 6x = 0 3x(x + 2) = 0 3x = 0 x + 2 = 0 x = 0 x = -2
1.1 Tweedegraadsvergelijkingen [1] Er zijn vier soorten tweedegraadsvergelijkingen: 1. ax 2 + bx = 0 (Haal de x buiten de haakjes) Voorbeeld 1: 3x 2 + 6x = 0 3x(x + 2) = 0 3x = 0 x + 2 = 0 x = 0 x = -2
Hoofdstuk 1 Beweging in beeld. Gemaakt als toevoeging op methode Natuurkunde Overal
 Hoofdstuk 1 Beweging in beeld Gemaakt als toevoeging op methode Natuurkunde Overal 1.4/1.5 Significantie en wiskundige vaardigheden Omrekenen van grootheden moet je kunnen. Onderstaande schema moet je
Hoofdstuk 1 Beweging in beeld Gemaakt als toevoeging op methode Natuurkunde Overal 1.4/1.5 Significantie en wiskundige vaardigheden Omrekenen van grootheden moet je kunnen. Onderstaande schema moet je
Hoe schrijf je de logaritmische waarden welke bij db s horen?
 Die moeilijke decibellen toch. PA0 FWN. Inleiding. Ondanks dat in Electron al vaak een artikel aan decibellen is geweid, en PA0 LQ in het verleden al eens een buitengewoon handige tabel publiceerde waar
Die moeilijke decibellen toch. PA0 FWN. Inleiding. Ondanks dat in Electron al vaak een artikel aan decibellen is geweid, en PA0 LQ in het verleden al eens een buitengewoon handige tabel publiceerde waar
( ) 8 ( ) 10. Nearby integers P.G. van de Veen, 19 juli en dát getal heeft al 960 cijfers voor de komma. Want. log 3 = 2010 log 3 > 959
 earby integers P.G. van de Veen, 19 juli 011 Hoeveel opeenvolgende negens heeft ( + 3) 010 achter de komma Wat een vreemde vraag! Zijn dat er dan veel En hoe tel je ze Dit getal is toch veel te groot om
earby integers P.G. van de Veen, 19 juli 011 Hoeveel opeenvolgende negens heeft ( + 3) 010 achter de komma Wat een vreemde vraag! Zijn dat er dan veel En hoe tel je ze Dit getal is toch veel te groot om
De grafiek van een lineair verband is altijd een rechte lijn.
 2. Verbanden Verbanden Als er tussen twee variabelen x en y een verband bestaat kunnen we dat op meerdere manieren vastleggen: door een vergelijking, door een grafiek of door een tabel. Stel dat het verband
2. Verbanden Verbanden Als er tussen twee variabelen x en y een verband bestaat kunnen we dat op meerdere manieren vastleggen: door een vergelijking, door een grafiek of door een tabel. Stel dat het verband
Bijlage 11 - Toetsenmateriaal
 Bijlage - Toetsenmateriaal Toets Module In de eerste module worden de getallen behandeld: - Natuurlijke getallen en talstelsels - Gemiddelde - mediaan - Getallenas en assenstelsel - Gehele getallen met
Bijlage - Toetsenmateriaal Toets Module In de eerste module worden de getallen behandeld: - Natuurlijke getallen en talstelsels - Gemiddelde - mediaan - Getallenas en assenstelsel - Gehele getallen met
Examen HAVO. wiskunde B. tijdvak 1 donderdag 9 mei uur. Bij dit examen hoort een uitwerkbijlage.
 Eamen HVO 09 tijdvak donderdag 9 mei 3.30-6.30 uur wiskunde B Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 8 vragen. Voor dit eamen zijn maimaal 78 punten te behalen. Voor elk vraagnummer
Eamen HVO 09 tijdvak donderdag 9 mei 3.30-6.30 uur wiskunde B Bij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 8 vragen. Voor dit eamen zijn maimaal 78 punten te behalen. Voor elk vraagnummer
2. Optellen en aftrekken van gelijknamige breuken
 1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
Samenvatting Wiskunde B
 Bereken: Bereken algebraisch: Bereken eact: De opgave mag berekend worden met de hand of met de GR. Geef bij GR gebruik de ingevoerde formules en gebruikte opties. Kies op een eamen in dit geval voor berekenen
Bereken: Bereken algebraisch: Bereken eact: De opgave mag berekend worden met de hand of met de GR. Geef bij GR gebruik de ingevoerde formules en gebruikte opties. Kies op een eamen in dit geval voor berekenen
Rekenen. Grote en kleine getallen
 Rekenen Grote en kleine getallen In de elektrotechniek wordt vaak gewerkt met heel grote en heel kleine getallen. Het is dan niet te doen om die helemaal uit te schrijven. Er wordt dan een aanduiding bijgezet.
Rekenen Grote en kleine getallen In de elektrotechniek wordt vaak gewerkt met heel grote en heel kleine getallen. Het is dan niet te doen om die helemaal uit te schrijven. Er wordt dan een aanduiding bijgezet.
Transformaties van grafieken HAVO wiskunde B deel 2. Willem van Ravenstein Haags Montessori Lyceum (c) 2016
 Transformaties van grafieken HAVO wiskunde B deel Willem van Ravenstein 50075005 Haags Montessori Lyceum (c) 0 Inleiding In deze leerroute gaan we kijken naar goniometrische functies: De eenheidscirkel
Transformaties van grafieken HAVO wiskunde B deel Willem van Ravenstein 50075005 Haags Montessori Lyceum (c) 0 Inleiding In deze leerroute gaan we kijken naar goniometrische functies: De eenheidscirkel
