Als je, van achter naar voor, na iedere 3 cijfers een klein beetje ruimte laat, of je zet een punt, wordt het allemaal duidelijker.
|
|
|
- Monique Vedder
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Samenvatting leerjaar 4 hoofdstuk 1: Rekenen Grote getallen Grote getallen, zoals zijn niet eenvoudig te lezen. Je kunt je gemakkelijk vergissen in een nul meer of minder, met grote gevolgen. Als je, van achter naar voor, na iedere 3 cijfers een klein beetje ruimte laat, of je zet een punt, wordt het allemaal duidelijker Dit getal kun je ook schrijven als 5,3 miljard. Wetenschappelijke notatie Naarmate getallen groter worden, wordt het minder praktisch om ze op te schrijven. Bij geld is het nodig héél precies te zijn, maar wanneer het om liters water in een oceaan gaat, of kilo s zand in de woestijn, maakt het niet uit als je wat minder exact bent. In dat soort gevallen kunnen we de wetenschappelijke notatie gebruiken, je werkt dan met machten van 10 en schuift de komma op wordt dan 5, Het eerste getal is altijd groter of gelijk aan 1 en kleiner of gelijk aan 9, dan volgt een komma en daarna één decimaal, tenzij in de opgave anders wordt gevraagd. We sluiten af met 10 a ). De a staat voor het aantal plaatsen dat de komma opgeschoven moet worden. Bij een negatief getal voor a hebben we te maken met getallen kleiner dan 1. Zie onderstaande voorbeelden: = 3, ,00023 = 2, = 5, ,322 = 3, = 3, , = 6, Omgekeerd kan natuurlijk ook: 4, = , = 0, , = , = 0, , = 290 2, = 0,029
2 Tot slot, je kunt met je rekenmachine een berekening uitvoeren, waarbij het antwoord te groot is voor je scherm, zie hieronder. Je rekenmachine geeft als antwoord op de vraag: Hoeveel is 25 8? het antwoord: Dat is 1, Wanneer je deze vraag in een opgave krijgt, rond je normaal gesproken af op één decimaal: 1, Volgorde van bewerkingen Onthoud de volgende zin, en je weet altijd de volgorde van bewerkingen: Hoe H Haakjes Komen K Kwadraten / machten Wij W Wortels Van V Vermenigvuldigen Die D Delen Onvoldoendes O Optellen Af? A Aftrekken In een berekening voor je de volgende 4 stappen uit: 1. Reken alles uit wat tussen haakjes staat 2. Machtsverheffen en worteltrekken, van links naar rechts 3. Vermenigvuldigen en delen, van links naar rechts 4. Optellen en aftrekken, van links naar rechts Bij een berekening die onder een wortelteken staat, zoals 45, voer je éérst de berekening uit voordat je de wortel trekt. Bij dit voorbeeld is de uitkomst dus 9, niet 7. In je rekenmachine voer je dit als volgt in: 4 5 geeft als uitkomst 3. Let op: fout is 4 5 met uitkomst 7. Bij de eerste regel tel je 4 en 5 op en trek je de wortel van 9, bij de tweede regel tel je de wortel van 4 op bij 5.
3 De berekening voer je op de volgende manier in: (6 + 12) : (4-2) geeft als uitkomst 9 Let op: fout is : 4-2 met uitkomst 7. Bij de eerste regel bereken je en 4-2 en deel je 18 door 2, bij de tweede regel deel je 12 door 4, tel je 6 en 3 op en trek je 2 af van 9. Dan nu twee voorbeelden van het correct omgaan met rekenvolgorde, zonder je rekenmachine te gebruiken: Stap 1: haakjes Stap 2: machten / wortels Stap 3: vermenigvuldigen / delen Stap 4: optellen / aftrekken Als je niet weet wat 8 betekent, dit spreek je uit als de derdemachtswortel van 8. Je zoekt het getal waarvan de derde macht als uitkomst 8 heeft. Dat is natuurlijk 2, want 2 3 = = = 3, want 3 3 = = 2, want 2 4 = = 4, want 4 3 = = 3, want 3 4 = = 5, want 5 3 = = 4, want 4 4 = 256 Let op: 2 4 betekent niet 2 4 en is dus niet gelijk aan 8. Deze vergissing wordt vaak gemaakt. 2 4 betekent en is gelijk aan wil zeggen dat je 4 keer het cijfer 2 op moet schrijven en er tussen moet zetten.
4 Een tweede voorbeeld: = Stap 1: bereken alles tussen haakjes = Stap 2: bereken de wortel, onder de deelstreep vermenigvuldig je. = Stap 3: vermenigvuldigen = 3 Stap 4: delen Bij een breuk moet je eerst alles boven de deelstreep én onder de deelstreep uitrekenen. Dat mag gelijktijdig, zoals je hierboven ziet. Pas als dat gebeurd is, kun je de laatste deling uitvoeren, in dit geval 9 : 3. Wanneer je een opgave zonder rekenmachine moet maken, is het erg belangrijk stap voor stap te werken en alle tussenstappen ook op te schrijven. Doe je dat niet, verlies je daardoor punten. Breuken De optelsom kun je met behulp van de rekenmachine uitrekenen. Bij de Casio fx82ms gaat dat als volgt: =1 Wanneer je nu opnieuw op de knop een decimaal. In dit geval is dat 1,475. drukt, krijg je het antwoord als De optelsom 1 6 voer je als volgt in: = 8 Ook hier kun je met de knop getal, te weten 8, de uitkomst omzetten in een decimaal
5 Natuurlijk kun je breuken ook zonder rekenmachine optellen. Je maakt dan eerst de breuken gelijknamig. Wanneer je een breuk zowel boven als onder de streep met hetzelfde getal vermenigvuldigt, verandert er niets aan de waarde van de breuk. Deze eigenschap gebruik je bij het gelijknamig maken, zie onderstaand. 1 Door boven en onder de deelstreep te vermenigvuldigen met 5 en boven en onder de deelstreep te vermenigvuldigen met 8, hebben we de breuken gelijknamig gemaakt. Daarna nog optellen en vereenvoudigen. Het tweede voorbeeld gaat als volgt: Machten Bij het gebruik van machten moet je goed letten op het gebruik van mintekens en haakjes. Een paar voorbeelden: 6 2 = 6 6 = = -6 6 = -36 (-6) 2 = -6-6 = 36 -(6) 2 = -6 6 = = = = = -64 (-4) 3 = = -64 (-4) 4 = = 256
6 Eenheden van tijd De volgende tijdseenheden dien je te kennen: 1 millennium = 1000 jaar 1 eeuw = 100 jaar 1 jaar = 4 kwartalen 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 dagen 1 kwartaal = 13 weken 1 week = 7 dagen 1 dag = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden Om te zien of een maand 31 dagen heeft of niet, kun je de knokkels van je hand gebruiken. Je hand heeft 4 knokkels en 3 dalen tussen de knokkels in. Maak een vuist, zodat je knokkels goed zichtbaar zijn. Je begint op een knokkel. Dat is januari met 31 dagen. Dan volgt een dal: februari met 28 dagen (of 29 in een schrikkeljaar). Knokkel, maart met 31 dagen. Dal, april met 30 dagen. Knokkel, mei met 31 dagen. Dal, juni met 30 dagen. Knokkel, juli met 31 dagen. Je bent nu aan het einde van je hand gekomen, dus beginnen we van voren af aan. Knokkel, augustus met 31 dagen. Dal, september met 30 dagen. Knokkel, oktober met 31 dagen. Dal, november met 30 dagen. En we eindigen met een knokkel, december met 31 dagen. Rekenen met tijd Er is een groot verschil tussen 3,50 uur en 3:50 uur. In het eerste geval gaat het om drie-en-een-half uur, dus 3 uur en 30 minuten. In het tweede geval gaat het om 3 uur en 50 minuten. Let goed op of er een komma of een dubbele punt staat. Daaraan kun je het verschil zien. Een aantal voorbeelden van rekenen met tijd tref je hieronder aan. Hoeveel minuten is 3,30 uur? 3,75 uur is 3 uur en 0,30 uur = 180 minuten 0,30 60 = 18 minuten = 198 minuten
7 Hoeveel uur is 213 minuten? Of, op een andere manier: Reken 5,78 om naar uu:mm:ss: 213 : 60 = 3,55 uur 3,55 uur is 3 uur en 0,55 uur 0,55 60 = 33 minuten dus 3 uur en 33 minuten (3:33 uur) 213 : 60 = 3,55 uur 3 60 = 180 minuten = 33 minuten dus 3 uur en 33 minuten (3:33 uur) 5,78 uur is 5 uur en 0,78 uur 0,78 60 = 46,8 minuten 46,8 minuten is 46 min. en 0,80 min. 0,80 60 = 48 seconden dus het antwoord is 5:46:48 Reken 1,6 weken om naar dagen, uren en minuten: 1 week = 7 dagen 0,6 7 = 4,2 dagen 0,2 24 = 4,8 uur 0,8 60 = 48 minuten dus 11 dagen, 4 uur en 48 minuten Snelheden omrekenen Omrekenen van km/h naar m/s: delen door 3,6 Omrekenen van m/s naar km/h: vermenigvuldigen met 3,6 Waarom werken deze rekenregels? Het bewijs is eenvoudig: Er zitten 3600 secondes in een uur (60 minuten 60 seconden), dus om 1 meter per seconde om te rekenen naar kilometers per uur, gebruik je een verhoudingstabel, waarin je boven en onder vermenigvuldigt met het getal meter 3600 meter 3,6 kilometer seconde 3600 secondes uur De laatste kolom is alleen omrekenen van meter naar kilometer en van secondes naar uren. Hiermee het bewijs: 1 m/s = 3,6 km/h.
8 Vergrotingsfactor Hieronder zie je drie vormen, te weten een lijn van 4 centimeter, een vierkant van 4 bij 4 centimeter en een kubus van 4 bij 4 bij 4 centimeter. Hieronder staan wederom een lijn, vierkant en kubus. Deze zijn met een factor 3 vergroot.
9 De lijn is nu dus 4 3 = 12 centimeter lang. Het vierkant is 12 bij 12. Is de oppervlakte van het vierkant nu ook 3 groter geworden? Je zou denken van wel, maar dat blijkt niet te kloppen. oppervlakte kleine vierkant: 4 4 = 16 cm 2 oppervlakte grote vierkant: = 144 cm : 16 = 9 Dus, de oppervlakte van het vierkant is 9 groter geworden. Dat komt omdat de vergrotingsfactor in de lengte én in de breedte werkt. De vergroting van de oppervlakte is dus de vergrotingsfactor in het kwadraat. Controle: 3 2 is inderdaad 9. Bij de inhoud is de vergroting van de inhoud de vergrotingsfactor tot de macht 3, omdat de vergrotingsfactor daar in drie richtingen werkt. inhoud kleine kubus: = 64 cm 2 indoud grote kubus: = 1728 cm : 64 = 27 controle: 3 3 is inderdaad 27. vergrotingsfactor is lengte groot : lengte klein vergroting oppervlakte is vergrotingsfactor 2 vergroting inhoud is vergrotingsfactor 3 Omgekeerd werkt dit dus ook, zoals de volgende voorbeelden illustreren: De oppervlakte van een vijver op een maquette is 256 keer kleiner dan de werkelijkheid. Wat is de schaal van de maquette? vergrotingsfactor 2 = 256, dus vergrotingsfactor = 256 = 16 de schaal is dus 1 : 16
10 De inhoud van een modelwoning is 2,5 m 3. De schaal is 1 : 6. Wat is de inhoud van de woning? vergrotingsfactor is 6 en 6 3 = 216 2,5 216 = 540 m 3 Verhoudingen Met verhoudingen kun je bereken hoeveel je nodig hebt, bijvoorbeeld bij het aanmaken van limonade of het mengen van verf. Daarvoor gebruiken we dan ook een verhoudingstabel. In een verhoudingstabel mag je vermenigvuldigen en delen, mits je dat voor alle onderdelen hetzelfde doet. Bij het aanmaken van limonade gebruik je 7 delen water op 1 deel siroop. Je kunt dus ook zeggen, 7 dl water op 1 dl siroop. Wanneer we nu de hoeveelheid water met 2 vermenigvuldigen, moet ik dat ook met de hoeveelheid siroop doen, 14 dl water op 2 dl siroop. Doe je dat niet, klopt de verhouding niet meer. Een voorbeeld: Je wil oranje verf maken. Daarvoor meng je 3 delen rood, 4 delen geel en 1 deel wit. Hoeveel heb je van alles nodig wanneer je 5 liter verf nodig hebt? : 8 5 Rood 3 1,875 liter Geel 4 2,5 liter Wit 1 0,625 liter Oranje liter : 8 5
11 De uitkomsten 3 : 8, 4 : 8 en 1 : 8 zijn niet van belang, die vullen we dus ook niet in. Je rekent uit 3 : 8 5 en 4 : 8 5 en 1 : 8 5. Op dezelfde manier bereken je de verhouding in procenten: : 8 100% Rood 3 37,5% Geel 4 50% Wit 1 12,5% Oranje % : 8 100% Natuurlijk kun je de procenten ook anders berekenen, namelijk: Rood: Geel: Wit: 100% = 37,5% 100% = 50,0% 100% = 12,5%
12 Breuk, deling en procenten Breuken, delingen en procenten hebben alles met elkaar te maken, zoals je bij het vorige onderdeel hebt kunnen zien. Daarom kunnen we ze in een tabel zetten. breuk deling uitkomst deling procenten : 8 0,125 12,5% 3 : 7 0, ,8% 4 : 5 0,8 80,0% Vanaf breuk naar deling, uitkomst en procenten werken is niet moeilijk, je kunt daarvoor je rekenmachine gebruiken. De omgekeerde volgorde is lastiger: wat als je alleen een percentage of de uitkomst van de deling weet? Stel je voor dat het percentage 37,5% is. De uitkomst van de deling is dan 37,5 : 100 = 0,375. Maar welke breuk hoort daar nu bij? In een breuk werken we alleen met hele getallen. Om van 0,375 een geheel getal te maken, moeten we de komma 3 plaatsen opschuiven en dus vermenigvuldigen met duizend. De breuk die daarbij hoort, gaan we vervolgens vereenvoudigen, zoals hieronder: De bijbehorende deling is vervolgens 3 : 8.
13 Grafen Een graaf is een schematisch tekening van bijvoorbeeld een wegennet waarin alleen de wegen, plaatsen en afstanden staan gegeven. Er wordt onderscheid gemaakt tussen twee graven, namelijk de gewogen en gerichte graaf. De gewogen graaf bevat getallen voor de afstanden, een gerichte graaf bevat daarnaast minimaal één eenrichtingsweg. Zie het voorbeeld hiernaast: Van A naar F = 3 Van B naar A = 6 Van A naar B moet via F = = 11 Kies altijd voor de kortste weg! A F 3 E G B D 3 C 2 Bij een graaf kun je een afstandstabel maken, en omgekeerd. AFSTANDSTABEL naar A B C D E F G A B C van D E F G
14 Op de volgende pagina s volgt een herhaling van de lesstof uit leerjaar 3, over het rekenen met procenten. Percentage berekenen Paco werkt bij een installatiebedrijf, hij monteert wastafelkranen in nieuwe huizen. Tijdens het testen blijken 12 van de 64 aangesloten kranen niet volledig af te sluiten. Het gaat om 12 van de 64, dus 64 is het geheel en 12 is daar een deel van. Je berekent het percentage met de volgende formule: percentage = deel : geheel 100% Hoeveel procent is 12 van de 64? Antwoord: 12 : % = 18,8% ofwel: 100% 18,8% Rekenen met procenten Noord-Brabant heeft ongeveer inwoners. Daarvan is ca. 89% katholiek (bron: CBS). Hoeveel inwoners zijn dat? Procent betekent letterlijk per honderd. Van iedere honderd inwoners zijn er dus 89 katholiek. De bijbehorende breuk is en dat is 0,89. deel = percentage : 100% geheel Hoeveel is 89% van ? Antwoord: 89 : 100 = 0,89 0, =
15 Procenten en korting Je gaat een nieuwe telefoon kopen. Deze kost 680,-. Neem je er echter een abonnement bij, krijg je 82% korting. Wat kost de telefoon dan nog? In plaats van het berekenen van de korting, gaan wij direct uitrekenen wat je nog moet betalen. Wanneer je 82% korting krijgt, betaal je nog 18%. Immers, 100% - 82% = 18%. Hoe je 18% van 680,- uitrekent, hebben we al behandeld. Hoeveel is 18% van 680,-? Antwoord: 18 : 100 = 0,18 0,18 680,- = 122,40 Procenten en prijsverhoging Een tablet kost in december 399,-. Per 1 januari gaat de prijs met 3% omhoog. Wat betaal je in januari voor deze tablet? Ook hier gaan we direct uitrekenen wat je moet betalen. Bij een stijging van 3%, betaal je 103%. Immers, 100% + 3% = 103%. Hoeveel is 103% van 399,-? Antwoord: 103 : 100 = 1,03 1,03 399,- = 410,97 Het klinkt raar dat je met meer dan 100% kunt rekenen. Als 100% het geheel is, hoe kun je dan meer hebben? Ik hoop dat je uit het voorbeeld snapt, dat het geheel zelf natuurlijk altijd groter kan worden. Ten opzichte van de beginsituatie (100%) zijn we nu dus gestegen tot boven 100%.
16 BTW Bij Makro zijn alle prijzen exclusief 19% BTW. Aan de kassa komt die BTW dus boven de prijs op het prijskaartje. Een X-Box 360 Kinect 4Gb is in de aanbieding voor 239,-, exclusief BTW. Wat is de prijs die je aan de kassa betaalt? De 21% BTW kunnen we zien als een prijsstijging, zie vorige paragraaf. 100% + 21% = 121% Hoeveel is 121% van 239,-? Antwoord: 121 : 100 = 1,21 1,21 239,- = 289,19 Promille Naast procent kennen we ook promille. Procent betekent per honderd, promille betekent per duizend. Alle rekenregels voor procent gelden ook voor promille. Je vervangt alleen het getal 100 door het getal Het teken voor promille is o oo Ook geldt: 1% =, 1o oo =, dus 1% = 10o oo. Deelnemers aan het verkeer kennen promille van de alcohol-limiet. Je mag als bestuurder niet meer dan 0,5 o oo alcohol in je bloed hebben. Dat is dus gelijk aan 0,05%. Jan drinkt 5 glazen bier van 25 cl. Het bier heeft een alcoholgehalte van 5%. Jan weegt 70 kg, 60% van zijn lichaam bestaat uit vocht. Wat is zijn alcoholpromillage? Mag hij autorijden? Dit probleem bestaat uit diverse onderdelen, die we stap voor stap op moeten lossen. Dat gaat als volgt:
17 Hoeveelheid alcohol in het bier: 25 cl = 250 ml ml = ml 5 : 100 = 0,05 0, = 62,5 ml Hoeveelheid vocht in het lichaam: 60 : 100 = 0,6 0,6 70 = 42 kg = 42 liter = ml Alcoholpromillage: promillage = deel : geheel 1000 Antwoord:, 1000o. oo = 1,5 o oo Conclusie: Jan mag dus niet autorijden! Exponentiële toename Stel je voor dat je een loterij wint, je ontvangt 750,-. Dit geld zet je op een spaarrekening. De bank geeft je 3,2% rente. Hoeveel staat er na 5 jaar op je rekening? Wat niet gaat werken, is uitrekenen hoeveel rente je het eerste jaar krijgt en dat bedrag vervolgens vermenigvuldigen met 5. Immers, de rente die je het eerste jaar krijgt, komt bij het bedrag op je bankrekening. Het tweede jaar ontvang je dus meer rente, het derde jaar nog meer, enz. Dat noemen we rente op rente.
18 Maar hoe rekenen we dit dan wel uit? Laten we beginnen met het bedrag na 1 jaar: 750,- is 100%. Er komt 3,2% bij. 100% + 3,2% = 103,2% 103,2 : 100 = 1, ,- 1,032 = 774,-, je hebt 24,- rente ontvangen. Na 2 jaar: 774,00 1,032 = 798,77 ( 24,77 rente) Na 3 jaar: 798,77 1,032 = 824,33 ( 25,56 rente) Na 4 jaar: 824,33 1,032 = 850,71 ( 26,38 rente) Na 5 jaar: 850,71 1,032 = 877,93 ( 27,22 rente) Er zitten twee nadelen aan bovenstaande methode. Hij is omslachtig en omdat je steeds tussentijds af moet ronden, is hij ook niet erg nauwkeurig. Het kan ook in één keer: 750,- 1,032 1,032 1,032 1,032 1,032 = 877,93 Je zult zeggen, daar komt hetzelfde uit. Maar dat is niet waar, zonder afronding komen er deze uitkomsten uit: 877,93272 en 877, , verschil 0, Dat is natuurlijk voor jou een miniem verschil, maar voor een bank die met miljarden werkt, gaat het om enorme bedragen. Laten we nog even terugkijken naar de berekening: 750,- 1,032 1,032 1,032 1,032 1,032 = 877,93
19 Hoewel dit de juiste uitkomst levert en korter is dan per jaar het bedrag uitrekenen, zoals we hebben gezien, blijft ook dit een omslachtige methode. Immers, stel je eens voor dat je moet uitrekenen hoeveel er na 20 jaar op je rekening staat. De berekening die je dan zou moeten maken, past niet eens op je rekenmachine. De oplossing is werken met machten. 1,032 2 = 1,032 1,032 1,032 3 = 1,032 1,032 1,032 1,032 4 = 1,032 1,032 1,032 1,032 1,032 5 = 1,032 1,032 1,032 1,032 1,032 Dus, wat staat er op de rekening? na 5 jaar: 750,- 1,032 5 = 877,93 na 20 jaar: 750,- 1, = 1.408,17 Op je rekenmachine voer je dat in als 750 1,032^5 of 750 1,032^20. Het bedrag waar je mee begint, noemen we het begingetal. Het getal waar je mee vermenigvuldigt, heet de groeifactor. In ons voorbeeld is het begingetal dus 750 en de groeifactor 1,032.
20 Een automerk verwacht een jaarlijkse groei van 2,8%. Ze verkopen nu auto s per jaar. Hoeveel auto s verkopen ze over 10 jaar? 100% + 2,8% = 102,8% 102,8% : 100 = 1, , = ,74 Antwoord: auto s We ronden af op het dichtstbijzijnde gehele getal, omdat je natuurlijk niet 0,74 auto kunt verkopen. Exponentiële afname Bij vermenigvuldigen met een getal groter dan 1, wordt het resultaat groter dan het beginpunt. Immers, 3 1,2 = 3,6 (3,6 is groter dan 3). Bij vermenigvuldigen met een getal kleiner dan 1, wordt het resultaat natuurlijk kleiner, 3 0,8 = 2,4 (2,4 is kleiner dan 3). Hetzelfde is waar bij machten. Dit blijkt ook uit de volgende voorbeelden. Zo geldt 1,01 50 = 1,64 en 0,99 50 =0,61. Waarom ga ik hier zo uitgebreid op in? Om je er goed van te doordringen dat vermenigvuldigen niet altijd betekent dat je ook vermeerdert. De conclusie die je hieruit kunt trekken, is dat een groeifactor groter dan 1 betekent dat er sprake is van groei. Bij een groeifactor kleiner dan 1 is er sprake van afname. Exponentiële toename: groeifactor > 1 Exponentiële afname: groeifactor < 1 > betekent groter dan, < betekent kleiner dan.
21 In 1998 leefde op de zuidpool een populatie pinguïns. Deze bestond uit dieren. Door een ziekte was er sprake van een jaarlijks afname van 1,7%. Hoe groot is de populatie in 2012? = 14 jaar 100% - 1,7% = 98,3% 98,3% : 100 = 0, , = ,39 Antwoord: pinguïns We ronden af op het dichtstbijzijnde gehele getal, omdat je natuurlijk geen 0,39 pinguïn kunt hebben. Procenten met verhoudingstabel Bij procenten hebben we tot nu toe steeds gerekend in situaties waarin de beginsituatie bekend was. Met andere woorden, we wisten wat er 100% was. Maar wat als je dat niet weet? In Schijndel wonen 5761 jongeren tussen 0 en 19 jaar (bron: CBS). Dat is 25,1% van de totale bevolking. Hoeveel inwoners heeft Schijndel? Een dergelijke opgave lossen we op met een verhoudingstabel. Zo n tabel werkt volgens het principe dat wat je aan de onderzijde van de tabel doet, je ook aan de bovenzijde moet doen. Hoe kom je nu van 25,1% naar 100%? Bij verhoudingen mag je nooit optellen of aftrekken, dus 74,9% erbij is niet de oplossing. Maar wat als je nu eerst deelt door 25,1 en daarna vermenigvuldigt met 100? Op die manier komen we op 100 uit, omdat 25,1 : 25,1 = 1 en = 100. Deze methode kun je in dit soort situaties altijd toepassen, zoals je op de volgende pagina's in de verschillende voorbeelden kunt zien. In Schijndel wonen 5761 jongeren tussen 0 en 19 jaar (bron: CBS). Dat is 25,1% van de totale bevolking. Hoeveel inwoners heeft Schijndel?
22 : 25, ,1% 1% 100% : 25,1 100 Het vakje waar de uitkomst van de deling 5761 : 25,1 zou moeten staan is gearceerd. Dat doen we omdat we die uitkomst niet opschrijven, dat is namelijk een tussenuitkomst. Om het antwoord te berekenen, voeren we op de rekenmachine in één keer in: 5761 : 25,1 100 =. Als antwoord vinden we dan (uiteraard hebben we afgerond op een geheel getal omdat je nu eenmaal geen halve bewoners hebt.) Een Galaxy SII wordt 5% duurder en kost dan 628,95. Hoeveel kostte de telefoon vóór de prijsverhoging? : ,95 599,- 105% 1% 100% :
23 In dit voorbeeld zie je dat de prijs 5% stijgt, en 100% + 5% = 105%. We delen dus eerst door 105 om op 1% uit te komen. De vervolgstap is altijd hetzelfde, namelijk vermenigvuldigen met 100 om op 100% uit te komen. Een Nintendo WII wordt 11% goedkoper en kost dan 209,15. Hoeveel kostte de gameconsole vóór de prijsverlaging? : ,15 235,- 89% 1% 100% :
SAMENVATTING BASIS & KADER
 SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
Elde college Schijndel. Kernteam Techniek
 Elde college Schijndel Kernteam Techniek Wiskunde lesstof stapelaars docent: Joost van Veghel Voorwoord Gefeliciteerd! Als je dit leest, heb je het schooljaar afgesloten met een diploma voor de basisberoepsgerichte
Elde college Schijndel Kernteam Techniek Wiskunde lesstof stapelaars docent: Joost van Veghel Voorwoord Gefeliciteerd! Als je dit leest, heb je het schooljaar afgesloten met een diploma voor de basisberoepsgerichte
Duizend 3 getallen achter de komma 230 duizend 230 000 46 duizend 46 000 Andersom 345 600 345,6 duizend 24 500 24,5 duizend
 Hoofdstuk 5 5A Grote getallen Duizend 3 getallen achter de komma 230 duizend 230 000 46 duizend 46 000 Andersom 345 600 345,6 duizend 24 500 24,5 duizend Miljoen 6 getallen achter de komma 230 miljoen
Hoofdstuk 5 5A Grote getallen Duizend 3 getallen achter de komma 230 duizend 230 000 46 duizend 46 000 Andersom 345 600 345,6 duizend 24 500 24,5 duizend Miljoen 6 getallen achter de komma 230 miljoen
Hoofdstuk 1: Basisvaardigheden
 Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
1.Tijdsduur. maanden:
 1.Tijdsduur 1 etmaal = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden 1 uur = 3600 seconden 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 (of 366 in schrikkeljaar) dagen 1 jaar = 4 kwartalen 1 kwartaal
1.Tijdsduur 1 etmaal = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden 1 uur = 3600 seconden 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 (of 366 in schrikkeljaar) dagen 1 jaar = 4 kwartalen 1 kwartaal
Hoe maak je nu van breuken procenten? Voorbeeld: Opgave: hoeveel procent van de onderstaande tekening is zwart gekleurd?
 Procenten Zoals op de basisschool is aangeleerd kunnen we een taart verdelen in een aantal stukken. Hierbij krijgen we een breuk. We kunnen ditzelfde stuk taart ook aangegeven als een percentage. Procenten:
Procenten Zoals op de basisschool is aangeleerd kunnen we een taart verdelen in een aantal stukken. Hierbij krijgen we een breuk. We kunnen ditzelfde stuk taart ook aangegeven als een percentage. Procenten:
1 Rekenen met gehele getallen
 1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
2 REKENEN MET BREUKEN 3. 2.3 Optellen van breuken 6. 2.5 Aftrekken van breuken 9. 2.7 Vermenigvuldigen van breuken 11. 2.9 Delen van breuken 13
 REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
REKENEN Hfst 1-3 PROCENTEN. Procenten betekent per honderd.
 REKENEN Hfst 1-3 PROCENTEN Procenten betekent per honderd. Percentage Groeifactor 1% 1/100 0,01 2% 2/100 0,02 10% 10/100 0,10 99% 99/100 0,99 104% 104/100 1,04 150% 150/100 1,50 Rekenen met procenten:
REKENEN Hfst 1-3 PROCENTEN Procenten betekent per honderd. Percentage Groeifactor 1% 1/100 0,01 2% 2/100 0,02 10% 10/100 0,10 99% 99/100 0,99 104% 104/100 1,04 150% 150/100 1,50 Rekenen met procenten:
Uitwerkingen Rekenen met cijfers en letters
 Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
1.1 Rekenen met letters [1]
![1.1 Rekenen met letters [1] 1.1 Rekenen met letters [1]](/thumbs/41/22623929.jpg) 1.1 Rekenen met letters [1] Voorbeeld 1: Een kaars heeft een lengte van 30 centimeter. Per uur brand er 6 centimeter van de kaars op. Hieruit volgt de volgende woordformule: Lengte in cm = -6 aantal branduren
1.1 Rekenen met letters [1] Voorbeeld 1: Een kaars heeft een lengte van 30 centimeter. Per uur brand er 6 centimeter van de kaars op. Hieruit volgt de volgende woordformule: Lengte in cm = -6 aantal branduren
1. Optellen en aftrekken
 1. Optellen en aftrekken Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers': Om de breuken met 'derden' en 'vijfden'
1. Optellen en aftrekken Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers': Om de breuken met 'derden' en 'vijfden'
2. Optellen en aftrekken van gelijknamige breuken
 1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
Basisvaardigheden algebra. Willem van Ravenstein. 2012 Den Haag
 Basisvaardigheden algebra Willem van Ravenstein 2012 Den Haag 1. Variabelen Rekenenis het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken
Basisvaardigheden algebra Willem van Ravenstein 2012 Den Haag 1. Variabelen Rekenenis het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken
4.1 Negatieve getallen vermenigvuldigen [1]
![4.1 Negatieve getallen vermenigvuldigen [1] 4.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/28/12962825.jpg) 4.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 x 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5 x -3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 x 3 = -15 Afspraak: In plaats
4.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 x 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5 x -3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 x 3 = -15 Afspraak: In plaats
Inhoud. Eenheden... 2 Omrekenen van eenheden I... 4 Omrekenen van eenheden II... 9 Omrekenen van eenheden III... 10
 Inhoud Eenheden... 2 Omrekenen van eenheden I... 4 Omrekenen van eenheden II... 9 Omrekenen van eenheden III... 10 1/10 Eenheden Iedere grootheid heeft zijn eigen eenheid. Vaak zijn er meerdere eenheden
Inhoud Eenheden... 2 Omrekenen van eenheden I... 4 Omrekenen van eenheden II... 9 Omrekenen van eenheden III... 10 1/10 Eenheden Iedere grootheid heeft zijn eigen eenheid. Vaak zijn er meerdere eenheden
3.1 Haakjes wegwerken [1]
![3.1 Haakjes wegwerken [1] 3.1 Haakjes wegwerken [1]](/thumbs/53/31611347.jpg) 3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
EXACT- Periode 1. Hoofdstuk Grootheden. 1.2 Eenheden.
 EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
7. 123 187 45 - - - - - - + 355 8. 35/595\17 59 35 245 245
 Antwoorden CITO 14-15 1. 295 187 - - - - - - + 482 2. 11/935\85 93 Hoe vaak past 11 in 93 88 8*11=88, dit is het grootste getal dat we van 93 af kunnen halen. 55 93-88=5 dan schuiven we de andere 5 ook
Antwoorden CITO 14-15 1. 295 187 - - - - - - + 482 2. 11/935\85 93 Hoe vaak past 11 in 93 88 8*11=88, dit is het grootste getal dat we van 93 af kunnen halen. 55 93-88=5 dan schuiven we de andere 5 ook
Toets gecijferdheid augustus 2005
 Toets gecijferdheid augustus 2005 Naam: Klas: score: Datum: Algemene aanwijzingen: - Noteer alle berekeningen en oplossingen in dit boekje - Blijf niet te lang zoeken naar een oplossing - Denk aan de tijd
Toets gecijferdheid augustus 2005 Naam: Klas: score: Datum: Algemene aanwijzingen: - Noteer alle berekeningen en oplossingen in dit boekje - Blijf niet te lang zoeken naar een oplossing - Denk aan de tijd
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/31/15201373.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
1 Basisrekenen en letterrekenen.
 Uitwerkingen versie 0 Basisrekenen en letterrekenen. Opgave. Opbouw van getallen. a 605 6 00 + 5 b 3.78 3 000+ 00+ 7 0+ 8 c 56.890 56 000+ 8 00+ 9 0+ 0 d 900.30 900 000+ 00+ 0+ 0 e 3.56.675 3.000.000+
Uitwerkingen versie 0 Basisrekenen en letterrekenen. Opgave. Opbouw van getallen. a 605 6 00 + 5 b 3.78 3 000+ 00+ 7 0+ 8 c 56.890 56 000+ 8 00+ 9 0+ 0 d 900.30 900 000+ 00+ 0+ 0 e 3.56.675 3.000.000+
Reken zeker: leerlijn kommagetallen
 Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Voorkennis : Breuken en letters
 Hoofdstuk 1 Getallen en Variabelen (V4 Wis A) Pagina 1 van 13 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x = 12
Hoofdstuk 1 Getallen en Variabelen (V4 Wis A) Pagina 1 van 13 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x = 12
Rekenen met cijfers en letters
 Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Willem van Ravenstein
 Willem van Ravenstein 1. Variabelen Rekenen is het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken je de bewerkingen machtsverheffen en worteltrekken.
Willem van Ravenstein 1. Variabelen Rekenen is het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken je de bewerkingen machtsverheffen en worteltrekken.
Leerlijnen groep 7 Wereld in Getallen
 Leerlijnen groep 7 Wereld in Getallen 1 2 REKENEN Boek 7a: Blok 1 - week 1 in geldcontext 2 x 2,95 = / 4 x 2,95 = Optellen en aftrekken tot 10.000 - ciferend; met 2 of 3 getallen 4232 + 3635 + 745 = 1600
Leerlijnen groep 7 Wereld in Getallen 1 2 REKENEN Boek 7a: Blok 1 - week 1 in geldcontext 2 x 2,95 = / 4 x 2,95 = Optellen en aftrekken tot 10.000 - ciferend; met 2 of 3 getallen 4232 + 3635 + 745 = 1600
ALBERDINGK THIJM COLLEGE REKENGIDS. Basis en afspraken rekenen
 ALBERDINGK THIJM COLLEGE REKENGIDS Basis en afspraken rekenen VOORWOORD Deze rekengids is bedoeld als overzichtelijk naslagwerk voor leerlingen, ouders, docenten en alle anderen die met rekenen te maken
ALBERDINGK THIJM COLLEGE REKENGIDS Basis en afspraken rekenen VOORWOORD Deze rekengids is bedoeld als overzichtelijk naslagwerk voor leerlingen, ouders, docenten en alle anderen die met rekenen te maken
In dit stuk worden een aantal berekeningen behandeld, die voor verschillende kostenberekeningen noodzakelijk zijn:
 BEREKENINGEN In dit stuk worden een aantal berekeningen behandeld, die voor verschillende kostenberekeningen noodzakelijk zijn: Behandeld worden: Machtsverheffen Berekeningen met verhoudingen Vergelijkingen
BEREKENINGEN In dit stuk worden een aantal berekeningen behandeld, die voor verschillende kostenberekeningen noodzakelijk zijn: Behandeld worden: Machtsverheffen Berekeningen met verhoudingen Vergelijkingen
Exact periode = 1. h = 0, Js. h= 6, Js 12 * 12 = 1,4.10 2
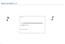 Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Rekentermen en tekens
 Rekentermen en tekens Erbij de som is hetzelfde, is evenveel, is gelijk aan Eraf het verschil, korting is niet hetzelfde, is niet evenveel Keer het product kleiner dan, minder dan; wijst naar het kleinste
Rekentermen en tekens Erbij de som is hetzelfde, is evenveel, is gelijk aan Eraf het verschil, korting is niet hetzelfde, is niet evenveel Keer het product kleiner dan, minder dan; wijst naar het kleinste
Leerstofplanning. 3 vmbo-k
 Leerstofplanning 3 vmbo-k Inhoud 3 vmbo-k deel 1 1 Kijken in ruimtefiguren Bij kaart: schaal, hemelsbreed en werkelijke afstand(vuistregels), hoogtelijnen op kaart, verticale doorsnede bij hoogtekaart,
Leerstofplanning 3 vmbo-k Inhoud 3 vmbo-k deel 1 1 Kijken in ruimtefiguren Bij kaart: schaal, hemelsbreed en werkelijke afstand(vuistregels), hoogtelijnen op kaart, verticale doorsnede bij hoogtekaart,
(o.a. voor 2F en 3F) Inhoud
 (o.a. voor 2F en 3F) Inhoud Optellen... 2 Aftrekken... 3 Vermenigvuldigen... 4 Delen... 5 Tot de macht... 6 Combinaties... 7 Wortels... 7 Afronden... 8 Breuken... 10 Procenten... 11 Verhoudingen... 12
(o.a. voor 2F en 3F) Inhoud Optellen... 2 Aftrekken... 3 Vermenigvuldigen... 4 Delen... 5 Tot de macht... 6 Combinaties... 7 Wortels... 7 Afronden... 8 Breuken... 10 Procenten... 11 Verhoudingen... 12
Reken zeker: leerlijn kommagetallen
 Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Doe eenvoudige opgaven zonder een rekenmachine. XX. Gebruik een rekenmachine bij moeilijke opgaven. Controleer de berekening door te schatten.
 1.2 Vermenigvuldigen Binnen de retail gebruik je een rekenmachine om getallen of bedragen of aantallen te vermenigvuldigen of te delen. Daarnaast kun je met schatten controleren of de berekening klopt.
1.2 Vermenigvuldigen Binnen de retail gebruik je een rekenmachine om getallen of bedragen of aantallen te vermenigvuldigen of te delen. Daarnaast kun je met schatten controleren of de berekening klopt.
Leerlijnen groep 8 Wereld in Getallen
 Leerlijnen groep 8 Wereld in Getallen 1 2 3 4 REKENEN Boek 8a: Blok 1 - week 1 Oriëntatie - uitspreken en schrijven van getallen rond 1 miljoen - introductie miljard - helen uit een breuk halen 5/4 = -
Leerlijnen groep 8 Wereld in Getallen 1 2 3 4 REKENEN Boek 8a: Blok 1 - week 1 Oriëntatie - uitspreken en schrijven van getallen rond 1 miljoen - introductie miljard - helen uit een breuk halen 5/4 = -
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/98/138669860.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
Klok dag en nacht. Hulpkaart OPTELLEN/AFTREKKEN
 OPTELLEN/AFTREKKEN Zet de getallen onder elkaar in je schrift eerst zelf proberen uit te rekenen bij aftrekken: denk om lenen bij optellen: denk om doorschuiven geen vergissingen? bij lang nadenken: rekenmachine
OPTELLEN/AFTREKKEN Zet de getallen onder elkaar in je schrift eerst zelf proberen uit te rekenen bij aftrekken: denk om lenen bij optellen: denk om doorschuiven geen vergissingen? bij lang nadenken: rekenmachine
Uitwerkingen oefeningen hoofdstuk 2
 Uitwerkingen oefeningen hoofdstuk 2 2.4.1 Basis Verhoudingen 1 13 cm : 390 km, dat is 13 cm : 390.000 m. Dat komt overeen met 13 cm : 39.000.000 cm en dat is te vereenvoudigen tot 1 : 3.000.000. 2 De schaal
Uitwerkingen oefeningen hoofdstuk 2 2.4.1 Basis Verhoudingen 1 13 cm : 390 km, dat is 13 cm : 390.000 m. Dat komt overeen met 13 cm : 39.000.000 cm en dat is te vereenvoudigen tot 1 : 3.000.000. 2 De schaal
mei 2009 Auteurs: P.C.M.M. Hosli B.D. De Wilde A.M.P. van de Luitgaarden Rekenvaardigheden: Inleiding bladzijde 1
 mei 2009 Auteurs: P.C.M.M. Hosli B.D. De Wilde A.M.P. van de Luitgaarden Rekenvaardigheden: Inleiding bladzijde 1 Inhoud Inleiding met docentenhandleiding Handleiding voor leerlingen Werkbladen en antwoordbladen
mei 2009 Auteurs: P.C.M.M. Hosli B.D. De Wilde A.M.P. van de Luitgaarden Rekenvaardigheden: Inleiding bladzijde 1 Inhoud Inleiding met docentenhandleiding Handleiding voor leerlingen Werkbladen en antwoordbladen
Rekenmachine. Willem-Jan van der Zanden
 Rekenmachine Vanaf hoofdstuk 5 mag je bij wiskunde bij bepaalde hoofdstukken een eenvoudige rekenmachine gebruiken; Als je nog geen rekenmachine hebt, koop dan een CASIO fx; Heb je al een rekenmachine
Rekenmachine Vanaf hoofdstuk 5 mag je bij wiskunde bij bepaalde hoofdstukken een eenvoudige rekenmachine gebruiken; Als je nog geen rekenmachine hebt, koop dan een CASIO fx; Heb je al een rekenmachine
Onderwijsassistent REKENEN BASISVAARDIGHEDEN
 Onderwijsassistent REKENEN BASISVAARDIGHEDEN Verhoudingstabel Wat zijn verhoudingen Rekenen met de verhoudingstabel Kruisprodukten Wat zijn verhoudingen * * * 2 Aantal rollen 1 2 12 Aantal beschuiten 18
Onderwijsassistent REKENEN BASISVAARDIGHEDEN Verhoudingstabel Wat zijn verhoudingen Rekenen met de verhoudingstabel Kruisprodukten Wat zijn verhoudingen * * * 2 Aantal rollen 1 2 12 Aantal beschuiten 18
KENMERKENDE CIJFERS EN BENADERINGSREGELS
 Correctiesleutel 2.06-2.07 KENMERKENDE CIJFERS EN BENADERINGSREGELS 1 Geef telkens telkens het kenmerkend deel, het aantal kenmerkende cijfers en de meetnauwkeurigheid. [De volgorde van opgaven en oplossingen
Correctiesleutel 2.06-2.07 KENMERKENDE CIJFERS EN BENADERINGSREGELS 1 Geef telkens telkens het kenmerkend deel, het aantal kenmerkende cijfers en de meetnauwkeurigheid. [De volgorde van opgaven en oplossingen
D A G 1 : T W E E D O M E I N E N
 REKENEN 3F DAG 1 :TWEE DOMEINEN DAG 2 : TWEE DOMEINEN DAG 3: EXAMENTRAINING DAG 4:EXAMENTRAINING EN A FRONDING Programma: Voorstellen 13.30 uur 16.15 uur Pauze: 15 minuten Theorie dag 1: Domein Getallen
REKENEN 3F DAG 1 :TWEE DOMEINEN DAG 2 : TWEE DOMEINEN DAG 3: EXAMENTRAINING DAG 4:EXAMENTRAINING EN A FRONDING Programma: Voorstellen 13.30 uur 16.15 uur Pauze: 15 minuten Theorie dag 1: Domein Getallen
Inhoud. 1 Ruimtefiguren 8. 4 Lijnen en hoeken 148. 2 Plaats bepalen 60. 5 Negatieve getallen 198. 3 Rekenen 100
 1 BK deel 1 Voorkennis 1 Aan de slag met wiskunde 6 1 Ruimtefiguren 8 1.1 Wiskundige ruimte guren 10 1.2 Vlakken, ribben en hoekpunten 14 1.3 Kubus en vierkant 17 1.4 Balk en rechthoek 24 1.5 Cilinder
1 BK deel 1 Voorkennis 1 Aan de slag met wiskunde 6 1 Ruimtefiguren 8 1.1 Wiskundige ruimte guren 10 1.2 Vlakken, ribben en hoekpunten 14 1.3 Kubus en vierkant 17 1.4 Balk en rechthoek 24 1.5 Cilinder
5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2
![5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2 5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2](/thumbs/72/66414323.jpg) Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) = a b 5.1 Herleiden [1] Voorbeeld 1: (a + 5)(a 6) (a + 5)(-a + 7) = a 6a + 5a 30 ( a + 14a 5a + 35) = a 6a + 5a 30
Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) = a b 5.1 Herleiden [1] Voorbeeld 1: (a + 5)(a 6) (a + 5)(-a + 7) = a 6a + 5a 30 ( a + 14a 5a + 35) = a 6a + 5a 30
Getallen 1F Doelen Voorbeelden 2F Doelen Voorbeelden
 A Notatie en betekenis - Uitspraak, schrijfwijze en betekenis van, symbolen en relaties - Wiskundetaal gebruiken - de relaties groter/kleiner dan - breuknotatie met horizontale streep - teller, noemer,
A Notatie en betekenis - Uitspraak, schrijfwijze en betekenis van, symbolen en relaties - Wiskundetaal gebruiken - de relaties groter/kleiner dan - breuknotatie met horizontale streep - teller, noemer,
1.1 Lineaire vergelijkingen [1]
![1.1 Lineaire vergelijkingen [1] 1.1 Lineaire vergelijkingen [1]](/thumbs/62/47724253.jpg) 1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen:
![6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen:](/thumbs/55/36024360.jpg) 6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 1) Haakjes wegwerken 2) Vermenigvuldigen en delen van links naar rechts 3) Optellen en aftrekken van links naar rechts Schrijf ALLE stappen ONDER
6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 1) Haakjes wegwerken 2) Vermenigvuldigen en delen van links naar rechts 3) Optellen en aftrekken van links naar rechts Schrijf ALLE stappen ONDER
Hoofdstuk 1 : REKENEN
 1 / 6 H1 Rekenen Hoofdstuk 1 : REKENEN 1. Wat moet ik leren? (handboek p.3-34) 1.1 Het decimaal stelsel In verband met het decimaal stelsel: a) het grondtal van ons decimaal stelsel geven. b) benamingen
1 / 6 H1 Rekenen Hoofdstuk 1 : REKENEN 1. Wat moet ik leren? (handboek p.3-34) 1.1 Het decimaal stelsel In verband met het decimaal stelsel: a) het grondtal van ons decimaal stelsel geven. b) benamingen
Strategiekaarten. Deze strategiekaarten horen bij de ThiemeMeulenhoff-uitgave (ISBN 978 90 557 4642 2): Rekenen: een hele opgave, deel 2
 Deze strategiekaarten horen bij de ThiemeMeulenhoff-uitgave (ISBN 978 90 557 4642 2): Joep van Vugt Anneke Wösten Handig optellen; tribunesom* Bij optellen van bijna ronde getallen zoals 39, 198, 2993,..
Deze strategiekaarten horen bij de ThiemeMeulenhoff-uitgave (ISBN 978 90 557 4642 2): Joep van Vugt Anneke Wösten Handig optellen; tribunesom* Bij optellen van bijna ronde getallen zoals 39, 198, 2993,..
1.3 Rekenen met pijlen
 14 Getallen 1.3 Rekenen met pijlen 1.3.1 Het optellen van pijlen Jeweetnuwatdegetallenlijnisendat0nochpositiefnochnegatiefis. Wezullen nu een soort rekenen met pijlen gaan invoeren. We spreken af dat bij
14 Getallen 1.3 Rekenen met pijlen 1.3.1 Het optellen van pijlen Jeweetnuwatdegetallenlijnisendat0nochpositiefnochnegatiefis. Wezullen nu een soort rekenen met pijlen gaan invoeren. We spreken af dat bij
Voorkennis : Breuken en letters
 Hoofdstuk 1 Rekenregels en Verhoudingen (H4 Wis A) Pagina 1 van 11 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x
Hoofdstuk 1 Rekenregels en Verhoudingen (H4 Wis A) Pagina 1 van 11 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x
REKENVAARDIGHEID BRUGKLAS
 REKENVAARDIGHEID BRUGKLAS Schooljaar 008/009 Inhoud Uitleg bij het boekje Weektaak voor e week: optellen en aftrekken Weektaak voor e week: vermenigvuldigen Weektaak voor e week: delen en de staartdeling
REKENVAARDIGHEID BRUGKLAS Schooljaar 008/009 Inhoud Uitleg bij het boekje Weektaak voor e week: optellen en aftrekken Weektaak voor e week: vermenigvuldigen Weektaak voor e week: delen en de staartdeling
Examencursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO kan niet korter
 Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Het metriek stelsel. Grootheden en eenheden.
 Het metriek stelsel. Metriek komt van meten. Bij het metriek stelsel gaat het om maten, zoals lengte, breedte, hoogte, maar ook om gewicht of inhoud. Er zijn verschillende maten die je moet kennen en die
Het metriek stelsel. Metriek komt van meten. Bij het metriek stelsel gaat het om maten, zoals lengte, breedte, hoogte, maar ook om gewicht of inhoud. Er zijn verschillende maten die je moet kennen en die
Uitwerking toets rekenvaardigheid. Opgave 1 a. 7125,98 + 698,99 = Tip: Bij kommagetallen is het eenvoudiger om aan geld te denken.
 Uitwerking toets rekenvaardigheid Opgave a. 725,98 + 698,99 = Tip: Bij kommagetallen is het eenvoudiger om aan geld te denken. 725,98 + 698,99 = 725,98 + 700,0= 7824,97 Denk eraan ik doe er teveel bij
Uitwerking toets rekenvaardigheid Opgave a. 725,98 + 698,99 = Tip: Bij kommagetallen is het eenvoudiger om aan geld te denken. 725,98 + 698,99 = 725,98 + 700,0= 7824,97 Denk eraan ik doe er teveel bij
REKENTECHNIEKEN - OPLOSSINGEN
 REKENTECHNIEKEN - OPLOSSINGEN 1] 3,52 m + 13,6 cm =? 3,52 m 3,52 m - 2 13,6 cm 0,136 m - 3 3,656 m eindresultaat 3,66 m 2 cijfers na komma en afronden naar boven 3,52 m 352 cm - 0 13,6 cm 13,6 cm - 1 365,6
REKENTECHNIEKEN - OPLOSSINGEN 1] 3,52 m + 13,6 cm =? 3,52 m 3,52 m - 2 13,6 cm 0,136 m - 3 3,656 m eindresultaat 3,66 m 2 cijfers na komma en afronden naar boven 3,52 m 352 cm - 0 13,6 cm 13,6 cm - 1 365,6
Samenvatting Wiskunde Aantal onderwerpen
 Samenvatting Wiskunde Aantal onderwerpen Samenvatting door een scholier 2378 woorden 4 juni 2005 5,1 222 keer beoordeeld Vak Wiskunde Gelijkvormigheid Bij vergroten of verkleinen van een figuur worden
Samenvatting Wiskunde Aantal onderwerpen Samenvatting door een scholier 2378 woorden 4 juni 2005 5,1 222 keer beoordeeld Vak Wiskunde Gelijkvormigheid Bij vergroten of verkleinen van een figuur worden
Rekenen aan wortels Werkblad =
 Rekenen aan wortels Werkblad 546121 = Vooraf De vragen en opdrachten in dit werkblad die vooraf gegaan worden door, moeten schriftelijk worden beantwoord. Daarbij moet altijd duidelijk zijn hoe de antwoorden
Rekenen aan wortels Werkblad 546121 = Vooraf De vragen en opdrachten in dit werkblad die vooraf gegaan worden door, moeten schriftelijk worden beantwoord. Daarbij moet altijd duidelijk zijn hoe de antwoorden
Leerdoelen groep 7. Pluspunt rekenen
 Leerdoelen groep 7 Pluspunt rekenen NB. De leerdoelen van deze rekenmethode bieden wij de kinderen aan middels Denken in Doelen. Dat betekent dat we niet exact de blokken van de methode volgen, maar dat
Leerdoelen groep 7 Pluspunt rekenen NB. De leerdoelen van deze rekenmethode bieden wij de kinderen aan middels Denken in Doelen. Dat betekent dat we niet exact de blokken van de methode volgen, maar dat
Opdracht 2.1 a t/m c. Er zijn veel mogelijkheden. De vorm hoeft dus niet gelijk te zijn om toch een vierkant van dezelfde grootte te krijgen.
 Uitwerkingen hoofdstuk Gebroken getallen. Kennismaken met breuken.. Deel van geheel Opdracht. a t/m c. Er zijn veel mogelijkheden. De vorm hoeft dus niet gelijk te zijn om toch een vierkant van dezelfde
Uitwerkingen hoofdstuk Gebroken getallen. Kennismaken met breuken.. Deel van geheel Opdracht. a t/m c. Er zijn veel mogelijkheden. De vorm hoeft dus niet gelijk te zijn om toch een vierkant van dezelfde
10.1 Berekeningen met procenten [1]
![10.1 Berekeningen met procenten [1] 10.1 Berekeningen met procenten [1]](/thumbs/39/19064625.jpg) 10.1 Berekeningen met procenten [1] Voorbeeld 1: Hoeveel is 48% van 560? Dit is 0,48 560 = 268,8 Voorbeeld 2: Een broek van het merk Replay kost normaal 129,-. Deze week is het uitverkoop en krijg je 35%
10.1 Berekeningen met procenten [1] Voorbeeld 1: Hoeveel is 48% van 560? Dit is 0,48 560 = 268,8 Voorbeeld 2: Een broek van het merk Replay kost normaal 129,-. Deze week is het uitverkoop en krijg je 35%
Breuken met letters WISNET-HBO. update juli 2013
 Breuken met letters WISNET-HBO update juli 2013 De bedoeling van deze les is het repeteren met pen en papier van het werken met breuken. Steeds wordt bij gebruik van letters verondersteld dat de noemers
Breuken met letters WISNET-HBO update juli 2013 De bedoeling van deze les is het repeteren met pen en papier van het werken met breuken. Steeds wordt bij gebruik van letters verondersteld dat de noemers
Domeinbeschrijving rekenen
 Domeinbeschrijving rekenen Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 11 december 2007 Inleiding Dit document bevat een beschrijving van
Domeinbeschrijving rekenen Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 11 december 2007 Inleiding Dit document bevat een beschrijving van
Verkorte versie van de SYLLABUS REKENEN 2F EN 3F (VO en MBO, versie mei 2015) Aanpassing van product van CvTE
 Verkorte versie van de SYLLABUS REKENEN 2F EN 3F (VO en MBO, versie mei 2015) Aanpassing van product van CvTE 1. Inleiding Vanaf 1 oktober 2015 gelden nieuwe afspraken omtrent het rekenexamen 3F. De exameneisen
Verkorte versie van de SYLLABUS REKENEN 2F EN 3F (VO en MBO, versie mei 2015) Aanpassing van product van CvTE 1. Inleiding Vanaf 1 oktober 2015 gelden nieuwe afspraken omtrent het rekenexamen 3F. De exameneisen
De waarde van een plaats in een getal.
 Komma getallen. Toen je net op school leerde rekenen, wist je niet beter dan dat getallen heel waren. Dus een taart was een taart, een appel een appel en een peer een peer. Langzaam maar zeker werd dit
Komma getallen. Toen je net op school leerde rekenen, wist je niet beter dan dat getallen heel waren. Dus een taart was een taart, een appel een appel en een peer een peer. Langzaam maar zeker werd dit
2A LEERLIJN. leerjaar 1. tellen. optellen en aftrekken GROEPEREN VERMENIGVULDIGEN EN DELEN. plaats en waarde. handig rekenen 1 ORDENEN EN UITSPREKEN
 2A LEERLIJN leerjaar 1. 1. tellen 1.1 Tellen in groepjes 1.2 Vooruittellen en terugtellen 7. optellen en aftrekken 7.1 Optellen 7.2 Aftrekken 2. GROEPEREN 2.1 Groeperen en inwisselen 2.2 Springen met grotere
2A LEERLIJN leerjaar 1. 1. tellen 1.1 Tellen in groepjes 1.2 Vooruittellen en terugtellen 7. optellen en aftrekken 7.1 Optellen 7.2 Aftrekken 2. GROEPEREN 2.1 Groeperen en inwisselen 2.2 Springen met grotere
Scoreblad bewis 01. naam cursist: naam afnemer: werkpunt. niet goed. tellen. getalbegrip. algemeen 01 04. bewerking en. optellen en.
 Scoreblad bewis naam cursist: datum: naam afnemer: inhoud vraag opmerkingen OK werkpunt niet goed tellen eieren tellen in dozen van 10 getallen verder aanvullen in kralenketting getalbegrip getallen ertussen
Scoreblad bewis naam cursist: datum: naam afnemer: inhoud vraag opmerkingen OK werkpunt niet goed tellen eieren tellen in dozen van 10 getallen verder aanvullen in kralenketting getalbegrip getallen ertussen
LESFICHE 1. Handig rekenen. Lesfiche 1. 1 Procent & promille. 2 Afronden. Procent of percent (%) betekent letterlijk per honderd.
 Lesfiche 1 1 Procent & promille Handig rekenen Procent of percent (%) betekent letterlijk per honderd. 5 5 % is dus 5 per honderd. In breukvorm wordt dat of 0,05 als decimaal getal. Promille ( ) betekent
Lesfiche 1 1 Procent & promille Handig rekenen Procent of percent (%) betekent letterlijk per honderd. 5 5 % is dus 5 per honderd. In breukvorm wordt dat of 0,05 als decimaal getal. Promille ( ) betekent
Tussendoelen domein VERHOUDINGEN 38
 WISKUNDETAAL BIJ VERHOUDINGEN, BREUKEN EN PROCENTEN kan gegevens in een verhoudingstabel interpreteren en begrijpt hoe een verhoudingstabel kan worden gebruikt om verhoudingen weer te geven en te vergelijken.
WISKUNDETAAL BIJ VERHOUDINGEN, BREUKEN EN PROCENTEN kan gegevens in een verhoudingstabel interpreteren en begrijpt hoe een verhoudingstabel kan worden gebruikt om verhoudingen weer te geven en te vergelijken.
Gehele getallen: machtsverheffing en vierkantsworteltrekking
 4 Gehele getallen: machtsverheffing en vierkantsworteltrekking Dit kun je al gehele getallen vermenigvuldigen 2 afspraken i.v.m. de volgorde van de bewerkingen toepassen 3 regelmaat en patronen ontdekken
4 Gehele getallen: machtsverheffing en vierkantsworteltrekking Dit kun je al gehele getallen vermenigvuldigen 2 afspraken i.v.m. de volgorde van de bewerkingen toepassen 3 regelmaat en patronen ontdekken
Spiekboekje. Knowledgebridge Onderwijs Hein v.d. Velden
 Spiekboekje Knowledgebridge Onderwijs Hein v.d. Velden 1 rekenen tot 20 verliefde getallen verliefde getallen zijn samen 10 1+9= 2+8= 3+7= 10 4+6= 5+5= 0+10= 2 getallenlijn 20 + plus 7 + 6= 7 + 3 = 10
Spiekboekje Knowledgebridge Onderwijs Hein v.d. Velden 1 rekenen tot 20 verliefde getallen verliefde getallen zijn samen 10 1+9= 2+8= 3+7= 10 4+6= 5+5= 0+10= 2 getallenlijn 20 + plus 7 + 6= 7 + 3 = 10
HAVO 4 wiskunde A. Een checklist is een opsomming van de dingen die je moet kennen en kunnen. checklist SE1 wiskunde A.pdf
 HAVO 4 wiskunde A Een checklist is een opsomming van de dingen die je moet kennen en kunnen. checklist SE1 wiskunde A.pdf 1. rekenregels en verhoudingen Ik kan breuken vermenigvuldigen en delen. Ik ken
HAVO 4 wiskunde A Een checklist is een opsomming van de dingen die je moet kennen en kunnen. checklist SE1 wiskunde A.pdf 1. rekenregels en verhoudingen Ik kan breuken vermenigvuldigen en delen. Ik ken
De Wetenschappelijke notatie
 De Wetenschappelijke notatie Grote getallen zijn vaak lastig te lezen. Hoeveel is bijvoorbeeld 23000000000000? Eén manier om het lezen te vergemakkelijken is het zetten van puntjes of spaties: 23.000.000.000.000
De Wetenschappelijke notatie Grote getallen zijn vaak lastig te lezen. Hoeveel is bijvoorbeeld 23000000000000? Eén manier om het lezen te vergemakkelijken is het zetten van puntjes of spaties: 23.000.000.000.000
Leerlijnen rekenen: De wereld in getallen
 Leerlijnen rekenen: De wereld in getallen Groep 7(eerste helft) Getalbegrip - Telrij tot en met 1 000 000 - Uitspraak en schrijfwijze van de getallen (800 000 en 0,8 miljoen) - De opbouw en positiewaarde
Leerlijnen rekenen: De wereld in getallen Groep 7(eerste helft) Getalbegrip - Telrij tot en met 1 000 000 - Uitspraak en schrijfwijze van de getallen (800 000 en 0,8 miljoen) - De opbouw en positiewaarde
Deel C. Breuken. vermenigvuldigen en delen
 Deel C Breuken vermenigvuldigen en delen - 0 Sprongen op de getallenlijn. De sprongen op de getallenlijn zijn even groot. Schrijf passende breuken of helen bij de deelstreepjes. 0 Welk eindpunt wordt bereikt
Deel C Breuken vermenigvuldigen en delen - 0 Sprongen op de getallenlijn. De sprongen op de getallenlijn zijn even groot. Schrijf passende breuken of helen bij de deelstreepjes. 0 Welk eindpunt wordt bereikt
Rekenportfolio. Naam: cm 2. m 3 + = 1 _ 12
 Tytsjerksteradiel Rekenportfolio Naam: cm 2 1 5 7 + = 5 10 10 m 3 1 _ 12 X 5 1 + = 5 1 + Inhoudsopgave Voorwoord 3 Domein getallen 4 - Optellen, aftrekken, vermenigvuldigen en delen 5 - Breuken 6 - Rekenvolgorde
Tytsjerksteradiel Rekenportfolio Naam: cm 2 1 5 7 + = 5 10 10 m 3 1 _ 12 X 5 1 + = 5 1 + Inhoudsopgave Voorwoord 3 Domein getallen 4 - Optellen, aftrekken, vermenigvuldigen en delen 5 - Breuken 6 - Rekenvolgorde
1.1 Opbouw en naamgeving van decimale getallen. vijf honderd drie en twintig komma vier en twintig
 1 Rekenen met getallen decimaal getal kommagetal Onderwerpen - Opbouw en naamgeving van decimale getallen - Optellen en aftrekken - Negatieve getallen met toepassingen - Vermenigvuldigen en delen - Breuken,
1 Rekenen met getallen decimaal getal kommagetal Onderwerpen - Opbouw en naamgeving van decimale getallen - Optellen en aftrekken - Negatieve getallen met toepassingen - Vermenigvuldigen en delen - Breuken,
Tijd: seconden, minuten, uren, dagen, weken, maanden, jaren
 Uren, Dagen, Maanden, Jaren,. Tijd: seconden, minuten, uren, dagen, weken, maanden, jaren 1 minuut 60 seconden 1 uur 60 minuten 1 half uur 30 minuten 1 kwartier 15 minuten 1 dag (etmaal) 24 uren 1 week
Uren, Dagen, Maanden, Jaren,. Tijd: seconden, minuten, uren, dagen, weken, maanden, jaren 1 minuut 60 seconden 1 uur 60 minuten 1 half uur 30 minuten 1 kwartier 15 minuten 1 dag (etmaal) 24 uren 1 week
1 Inleiding 2 Lengte en zijn eenheden 3 Omtrek 4 Oppervlakte 5 Inhoud. Meten is weten. Joke Braaksma. November 2010
 November 2010 Wat kunnen we allemaal meten? Wat kunnen we allemaal meten? 1. Lengte / breedte / hoogte / omtrek / oppervlakte / inhoud en volume 2. Tijd 3. Gewicht 4. Geld 5. Temperatuur Wij gaan ons
November 2010 Wat kunnen we allemaal meten? Wat kunnen we allemaal meten? 1. Lengte / breedte / hoogte / omtrek / oppervlakte / inhoud en volume 2. Tijd 3. Gewicht 4. Geld 5. Temperatuur Wij gaan ons
HANDREIKING REKENEN 2F MBO
 HANDREIKING REKENEN 2F MBO TEN BEHOEVE VAN REKENONDERWIJS CENTRAAL ONTWIKKELDE EXAMENS pagina 2 van 24 Inhoud 1 Voorwoord 5 2 Algemeen 6 3 Domein getallen 7 4 Domein verhoudingen 9 5 Domein Meten en Meetkunde
HANDREIKING REKENEN 2F MBO TEN BEHOEVE VAN REKENONDERWIJS CENTRAAL ONTWIKKELDE EXAMENS pagina 2 van 24 Inhoud 1 Voorwoord 5 2 Algemeen 6 3 Domein getallen 7 4 Domein verhoudingen 9 5 Domein Meten en Meetkunde
Checklist Wiskunde A HAVO 4 2014-2015 HML
 Checklist Wiskunde A HAVO 4 2014-2015 HML 1 Hoofdstuk 1 Ik weet hoe je met procenten moet rekenen: procenten en breuken, percentage berekenen, toename en afname in procenten, rekenen met groeifactoren.
Checklist Wiskunde A HAVO 4 2014-2015 HML 1 Hoofdstuk 1 Ik weet hoe je met procenten moet rekenen: procenten en breuken, percentage berekenen, toename en afname in procenten, rekenen met groeifactoren.
Optellen van twee getallen onder de 10
 Splitsen tot 0 uit het hoofd 2 Optellen 2 7 6 2 5 3 4 Splitsen tot 20 3 2 8 7 2 6 3 5 4 4 4 3 2 2 9 8 2 7 3 6 4 5 5 4 2 3 0 9 2 8 3 7 4 6 5 5 6 5 2 4 3 3 Bij een aantal iets erbij doen heet optellen. Je
Splitsen tot 0 uit het hoofd 2 Optellen 2 7 6 2 5 3 4 Splitsen tot 20 3 2 8 7 2 6 3 5 4 4 4 3 2 2 9 8 2 7 3 6 4 5 5 4 2 3 0 9 2 8 3 7 4 6 5 5 6 5 2 4 3 3 Bij een aantal iets erbij doen heet optellen. Je
Kennemer College Beroepsgericht Programma van Toetsing en Afsluiting schooljaar Proefwerk 60 min 3 Ja Schriftelijk.
 Kennemer College Beroepsgericht Programma van Toetsing en Afsluiting schooljaar 2017 2018 Wiskunde 4 Basis Periode Wat moet je kennen en kunnen? (deel)taken Toets-vorm Duur Weging Herkan sing Wijze van
Kennemer College Beroepsgericht Programma van Toetsing en Afsluiting schooljaar 2017 2018 Wiskunde 4 Basis Periode Wat moet je kennen en kunnen? (deel)taken Toets-vorm Duur Weging Herkan sing Wijze van
Foutenberekeningen. Inhoudsopgave
 Inhoudsopgave Leerdoelen :... 3 1. Inleiding.... 4 2. De absolute fout... 5 3. De KOW-methode... 7 4. Grootheden optellen of aftrekken.... 8 5. De relatieve fout...10 6. grootheden vermenigvuldigen en
Inhoudsopgave Leerdoelen :... 3 1. Inleiding.... 4 2. De absolute fout... 5 3. De KOW-methode... 7 4. Grootheden optellen of aftrekken.... 8 5. De relatieve fout...10 6. grootheden vermenigvuldigen en
Toelatingsexamen. Vakcode: Wiskunde basis onderbouw. Tijdsduur: 2 uur en 30 minuten
 Toelatingsexamen VOORBLAD VOORBEELDEXAMEN Vakcode: Wiskunde basis onderbouw Tijdsduur: 2 uur en 30 minuten De volgende hulpmiddelen zijn toegestaan bij het examen: rekenmachine (maar geen grafische) kladpapier
Toelatingsexamen VOORBLAD VOORBEELDEXAMEN Vakcode: Wiskunde basis onderbouw Tijdsduur: 2 uur en 30 minuten De volgende hulpmiddelen zijn toegestaan bij het examen: rekenmachine (maar geen grafische) kladpapier
BEWERKINGEN HOOFDREKENEN 40 NATUURLIJKE GETALLEN OPTELLEN
 BEWERKINGEN HOOFDREKENEN 40 NATUURLIJKE GETALLEN OPTELLEN a De standaardprocedure: getallen splitsen Zo lukt het altijd: 98 + 476 = 98 + 400 + 70 + 6 = 698 + 70 + 6 = 768 + 6 = 774 b Van plaats wisselen
BEWERKINGEN HOOFDREKENEN 40 NATUURLIJKE GETALLEN OPTELLEN a De standaardprocedure: getallen splitsen Zo lukt het altijd: 98 + 476 = 98 + 400 + 70 + 6 = 698 + 70 + 6 = 768 + 6 = 774 b Van plaats wisselen
HAVO 4 wiskunde A. Een checklist is een opsomming van de dingen die je moet kennen en kunnen....
 HAVO 4 wiskunde A Een checklist is een opsomming van de dingen die je moet kennen en kunnen.... 1. rekenregels en verhoudingen Ik kan breuken vermenigvuldigen en delen. Ik ken de rekenregel breuk Ik kan
HAVO 4 wiskunde A Een checklist is een opsomming van de dingen die je moet kennen en kunnen.... 1. rekenregels en verhoudingen Ik kan breuken vermenigvuldigen en delen. Ik ken de rekenregel breuk Ik kan
1.1 Opbouw en naamgeving van decimale getallen. vijf honderd drie en twintig komma vier en twintig
 1 Rekenen met getallen decimaal getal kommagetal Onderwerpen - Opbouw en naamgeving van decimale getallen - Optellen en aftrekken - Negatieve getallen met toepassingen - Vermenigvuldigen en delen - Breuken,
1 Rekenen met getallen decimaal getal kommagetal Onderwerpen - Opbouw en naamgeving van decimale getallen - Optellen en aftrekken - Negatieve getallen met toepassingen - Vermenigvuldigen en delen - Breuken,
Hoofdstuk 5 gaat over rekenen. Deel 2 is eigenlijk herhaling van alle stof. Trainen voor het examen.
 Hoofdstuk 5 gaat over rekenen. Deel 2 is eigenlijk herhaling van alle stof. Trainen voor het examen. Het werkt als volgt, Je maakt een opgave bijv. opgave 1. Hoe gaat het ook al weer denk je dan. Nou,
Hoofdstuk 5 gaat over rekenen. Deel 2 is eigenlijk herhaling van alle stof. Trainen voor het examen. Het werkt als volgt, Je maakt een opgave bijv. opgave 1. Hoe gaat het ook al weer denk je dan. Nou,
kun je op verschillende manieren opschrijven of uitspreken: XX Daarnaast kun je een breuk ook opschrijven als een decimaal getal.
 . Breuken Je kunt breuken gebruiken om een verhouding weer te geven. Een breuk schrijf je als een streepje met een getal erboven (de teller) en een getal eronder (de noemer), bijvoorbeeld. De streep zelf
. Breuken Je kunt breuken gebruiken om een verhouding weer te geven. Een breuk schrijf je als een streepje met een getal erboven (de teller) en een getal eronder (de noemer), bijvoorbeeld. De streep zelf
RekenWijzer, uitwerkingen hoofdstuk 2 Gebroken getallen
 Uitwerkingen 2. Kennismaken met breuken 2.. Deel van geheel Opdracht B 8 deel. ( deel + 8 deel). Opdracht 2 C 5 deel Opdracht C Driehoek C past in driehoek A. Aangezien driehoek A deel is van de tekening,
Uitwerkingen 2. Kennismaken met breuken 2.. Deel van geheel Opdracht B 8 deel. ( deel + 8 deel). Opdracht 2 C 5 deel Opdracht C Driehoek C past in driehoek A. Aangezien driehoek A deel is van de tekening,
mei 16 19:37 Iedere keer is de groeifactor gelijk. (een factor is een getal in een vermenigvuldiging)
 Wiskunde 3VWO Hoofdstuk 8 par 8.1 par 8.2 Procenten en groeifactoren Niet par 8.3 Periodieke verbanden par 8.4 Machtsfuncties par 8.5 Grafieken veranderen par 8.6 Extreme waarden mei 16 19:37 Maandag zitten
Wiskunde 3VWO Hoofdstuk 8 par 8.1 par 8.2 Procenten en groeifactoren Niet par 8.3 Periodieke verbanden par 8.4 Machtsfuncties par 8.5 Grafieken veranderen par 8.6 Extreme waarden mei 16 19:37 Maandag zitten
Toetswijzer examen Cool 2.1
 Toetswijzer examen Cool 2.1 Cool 2.1 1 Getallenkennis: Grote natuurlijke getallen 86 a Ik kan grote getallen vlot lezen en schrijven. 90 b Ik kan getallen afronden. 91 c Ik ken de getalwaarde van een getal.
Toetswijzer examen Cool 2.1 Cool 2.1 1 Getallenkennis: Grote natuurlijke getallen 86 a Ik kan grote getallen vlot lezen en schrijven. 90 b Ik kan getallen afronden. 91 c Ik ken de getalwaarde van een getal.
2 Meten 2.1 2.1 Kaarten 2.1 2.2 Materialen en technieken 2.3 2.3 Meten en schetsen 2.12 2.4 Praktijkopdrachten 2.16
 Inhoud Voorwoord v Het metrieke stelsel vii Inhoud ix Trefwoordenlijst x 1 Basis 1.1 1.1 Veel voorkomende berekeningen 1.1 1.2 Van punt tot vlak 1.4 1.3 Oppervlakten berekenen 1.12 1.4 Zelf tekenen 1.16
Inhoud Voorwoord v Het metrieke stelsel vii Inhoud ix Trefwoordenlijst x 1 Basis 1.1 1.1 Veel voorkomende berekeningen 1.1 1.2 Van punt tot vlak 1.4 1.3 Oppervlakten berekenen 1.12 1.4 Zelf tekenen 1.16
BEWERKINGEN HOOFDREKENEN 40 NATUURLIJKE GETALLEN OPTELLEN
 40 NATUURLIJKE GETALLEN OPTELLEN a De standaardprocedure: getallen splitsen Zo lukt het altijd: 98 + 476 = 98 + 400 + 70 + 6 = 698 + 70 + 6 = 768 + 6 = 774 b Van plaats wisselen Uitsluitend te gebruiken
40 NATUURLIJKE GETALLEN OPTELLEN a De standaardprocedure: getallen splitsen Zo lukt het altijd: 98 + 476 = 98 + 400 + 70 + 6 = 698 + 70 + 6 = 768 + 6 = 774 b Van plaats wisselen Uitsluitend te gebruiken
Foutenberekeningen Allround-laboranten
 Allround-laboranten Inhoudsopgave INHOUDSOPGAVE... 2 LEERDOELEN :... 3 1. INLEIDING.... 4 2. DE ABSOLUTE FOUT... 5 3. DE KOW-METHODE... 6 4. DE RELATIEVE FOUT... 6 5. GROOTHEDEN VERMENIGVULDIGEN EN DELEN....
Allround-laboranten Inhoudsopgave INHOUDSOPGAVE... 2 LEERDOELEN :... 3 1. INLEIDING.... 4 2. DE ABSOLUTE FOUT... 5 3. DE KOW-METHODE... 6 4. DE RELATIEVE FOUT... 6 5. GROOTHEDEN VERMENIGVULDIGEN EN DELEN....
3.1 Negatieve getallen vermenigvuldigen [1]
![3.1 Negatieve getallen vermenigvuldigen [1] 3.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/101/149931282.jpg) 3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
x -3-2 -1 0 1 2 3 a. y -7-4 -1 2 5 8 11 b. y -3.5-3 -2.5-2 -1.5-1 -0.5 c. y 7 6 5 4 3 2 1
 Huiswerk bij les 1 1. Teken de grafiek van de volgende functies (maak eerste een tabel en ga dan tekenen): a. y = 3x +2 lineaire functie met startgetal 2 en helling 3 b. y = -2 + ½x lineaire functie met
Huiswerk bij les 1 1. Teken de grafiek van de volgende functies (maak eerste een tabel en ga dan tekenen): a. y = 3x +2 lineaire functie met startgetal 2 en helling 3 b. y = -2 + ½x lineaire functie met
